Unsupervised Learning: Principle Component Analysis

1 . Unsupervised Learning: Principle Component Analysis 

2 . Unsupervised Learning • Dimension Reduction • Generation (無中生有) (化繁為簡) only having function input only having function function output function Random numbers 

3 .Dimension Reduction vector x function vector z (High Dim) (Low Dim) Looks like 3-D Actually, 2-D 

4 .Dimension Reduction • In MNIST, a digit is 28 x 28 dims. • Most 28 x 28 dim vectors are not digits 3 -20。 -10。 0。 10。 20。 

5 . 0 Cluster 3 0 Clustering 1 1 Open question: how many 0 0 clusters do we need? 1 0 0 Cluster 1 Cluster 2 • K-means • Clustering 𝑋 = 𝑥 1 , ⋯ , 𝑥 𝑛 , ⋯ , 𝑥 𝑁 into K clusters • Initialize cluster center 𝑐 𝑖 , i=1,2, … K (K random 𝑥 𝑛 from 𝑋) • Repeat 𝑛 is most “close” to 𝑐 𝑖 1 𝑥 • For all 𝑥 𝑛 in 𝑋: 𝑏𝑖𝑛 0 Otherwise • Updating all 𝑐 𝑖 : 𝑐 𝑖 = ෍ 𝑏 𝑛 𝑥 𝑛 ൘෍ 𝑏 𝑛 𝑖 𝑖 𝑥𝑛 𝑥𝑛 

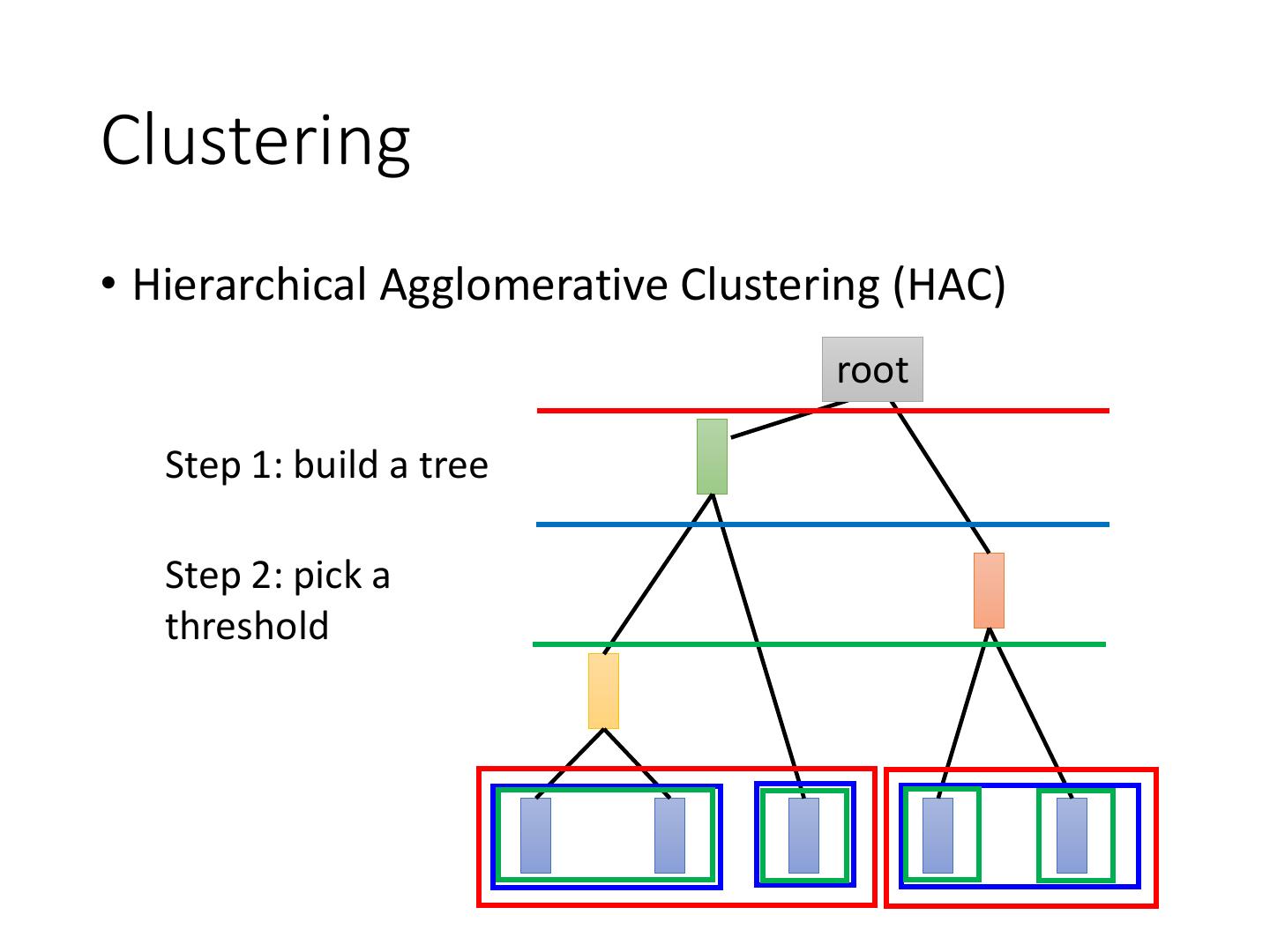
6 .Clustering • Hierarchical Agglomerative Clustering (HAC) root Step 1: build a tree Step 2: pick a threshold 

7 .Distributed Representation • Clustering: an object must belong to one cluster 小傑是強化系 • Distributed representation 強化系 0.70 放出系 0.25 變化系 0.05 小傑是 操作系 0.00 具現化系 0.00 特質系 0.00 

8 .Distributed Representation vector x function vector z (High Dim) (Low Dim) 𝑥2 • Feature selection Select 𝑥2 ? 𝑥1 • Principle component analysis (PCA) [Bishop, Chapter 12] 𝑧 = 𝑊𝑥 

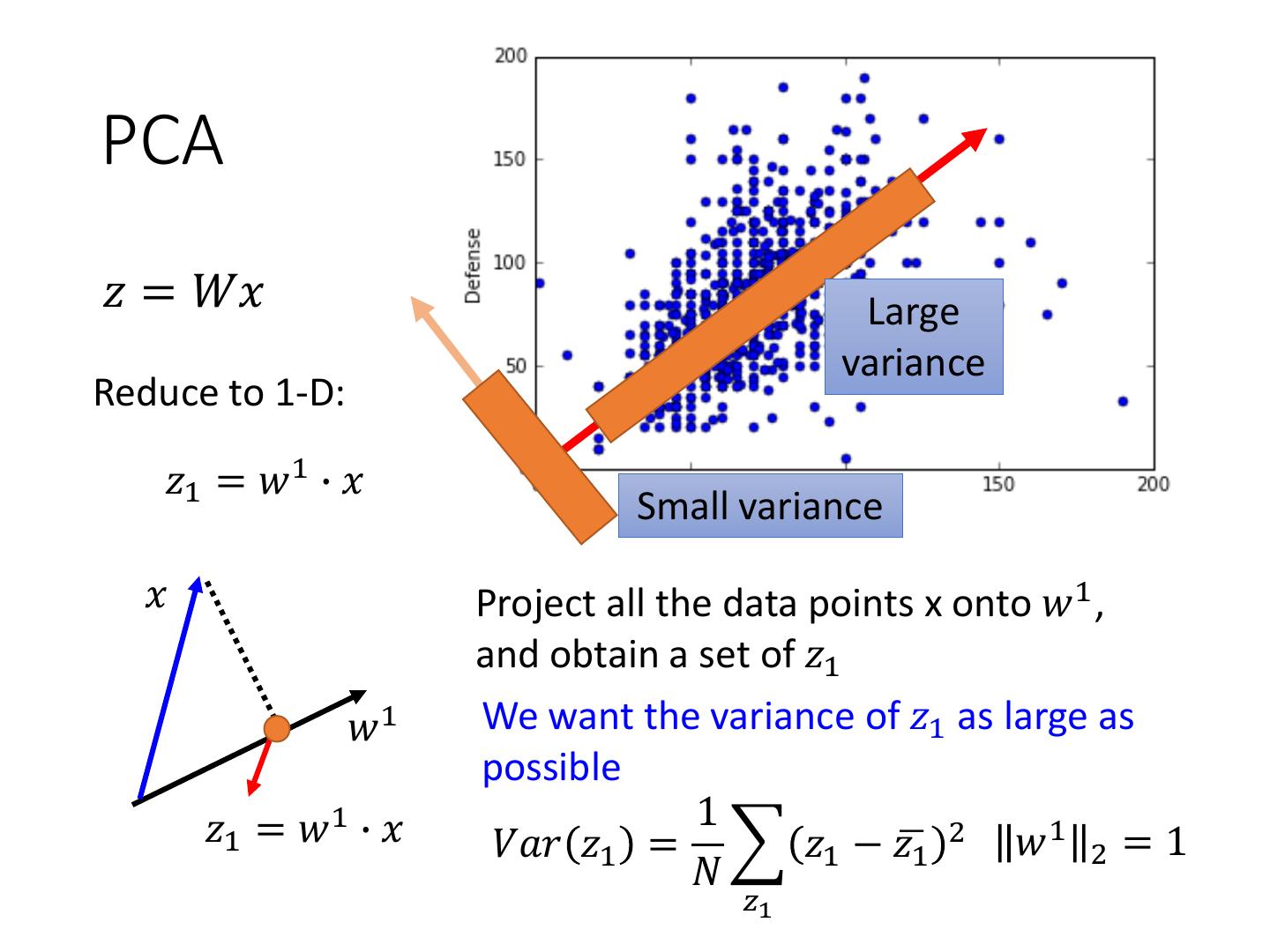
9 .PCA 𝑧 = 𝑊𝑥 Large variance Reduce to 1-D: 𝑧1 = 𝑤 1 ∙ 𝑥 Small variance 𝑥 Project all the data points x onto 𝑤 1 , and obtain a set of 𝑧1 𝑤1 We want the variance of 𝑧1 as large as possible 𝑧1 = 𝑤 1 ∙ 𝑥 1 𝑉𝑎𝑟 𝑧1 = ෍ 𝑧1 − 𝑧ഥ1 2 𝑤 1 2 = 1 𝑁 𝑧1 

10 .PCA Project all the data points x onto 𝑤 1 , and obtain a set of 𝑧1 We want the variance of 𝑧1 as large as 𝑧 = 𝑊𝑥 possible 1 1 Reduce to 1-D: 𝑉𝑎𝑟 𝑧1 = ෍ 𝑧1 − 𝑧ഥ1 2 𝑤 2 =1 𝑁 𝑧1 𝑧1 = 𝑤1 ∙𝑥 𝑧2 = 𝑤 2 ∙ 𝑥 We want the variance of 𝑧2 as large as possible 𝑤1 𝑇 𝑊= 1 𝑤2 𝑇 𝑉𝑎𝑟 𝑧2 = ෍ 𝑧2 − 𝑧ഥ2 2 𝑤2 2 =1 𝑁 ⋮ 𝑧2 𝑤1 ∙ 𝑤2 = 0 Orthogonal matrix 

11 .Warning of Math 

12 . 𝑧1 = 𝑤 1 ∙ 𝑥 PCA 1 1 1 1 1 𝑧ഥ1 = ෍ 𝑧1 = ෍ 𝑤 ∙ 𝑥 = 𝑤 ∙ ෍ 𝑥 = 𝑤 1 ∙ 𝑥ҧ 𝑁 𝑁 𝑁 1 𝑉𝑎𝑟 𝑧1 = ෍ 𝑧1 − 𝑧ഥ1 2 𝑁 𝑧1 𝑎 ∙ 𝑏 2 = 𝑎𝑇 𝑏 2 = 𝑎𝑇 𝑏𝑎𝑇 𝑏 1 = ෍ 𝑤 1 ∙ 𝑥 − 𝑤 1 ∙ 𝑥ҧ 2 = 𝑎𝑇 𝑏 𝑎𝑇 𝑏 𝑇 = 𝑎𝑇 𝑏𝑏 𝑇 𝑎 𝑁 𝑥 1 1 2 = ෍ 𝑤 ∙ 𝑥 − 𝑥ҧ 𝑁 Find 𝑤 1 maximizing 1 = ෍ 𝑤 1 𝑇 𝑥 − 𝑥ҧ 𝑥 − 𝑥ҧ 𝑇 𝑤 1 𝑤 1 𝑇 𝑆𝑤 1 𝑁 1 𝑇 1 𝑤1 2 = 𝑤1 𝑇 𝑤1 = 1 = 𝑤 ෍ 𝑥 − 𝑥ҧ 𝑥 − 𝑥ҧ 𝑇 𝑤 1 𝑁 = 𝑤 1 𝑇 𝐶𝑜𝑣 𝑥 𝑤 1 𝑆 = 𝐶𝑜𝑣 𝑥 

13 .Find 𝑤 1 maximizing 𝑤 1 𝑇 𝑆𝑤 1 𝑤1 𝑇 𝑤1 = 1 𝑆 = 𝐶𝑜𝑣 𝑥 Symmetric Positive-semidefinite (non-negative eigenvalues) Using Lagrange multiplier [Bishop, Appendix E] 𝑔 𝑤 1 = 𝑤 1 𝑇 𝑆𝑤 1 − 𝛼 𝑤 1 𝑇 𝑤 1 − 1 𝜕𝑔 𝑤1 Τ𝜕𝑤11 =0 𝑆𝑤 1 − 𝛼𝑤 1 = 0 𝑆𝑤 1 = 𝛼𝑤 1 𝑤 1 : eigenvector 𝜕𝑔 𝑤 1 Τ𝜕𝑤21 = 0 𝑤 1 𝑇 𝑆𝑤 1 = 𝛼 𝑤 1 𝑇 𝑤 1 … =𝛼 Choose the maximum one 𝑤 1 is the eigenvector of the covariance matrix S Corresponding to the largest eigenvalue 𝜆1 

14 .Find 𝑤 2 maximizing 𝑤 2 𝑇 𝑆𝑤 2 𝑤2 𝑇𝑤2 = 1 𝑤 2 𝑇 𝑤1 = 0 𝑔 𝑤 2 = 𝑤 2 𝑇 𝑆𝑤 2 − 𝛼 𝑤 2 𝑇 𝑤 2 − 1 −𝛽 𝑤 2 𝑇 𝑤 1 − 0 𝜕𝑔 𝑤 2 Τ𝜕𝑤12 = 0 𝑆𝑤 2 − 𝛼𝑤 2 − 𝛽𝑤 1 = 0 𝑤 1 0𝑇 𝑆𝑤 2 − 𝛼 𝑤 1 0𝑇 𝑤 2 − 𝛽 𝑤 11𝑇 𝑤 1 = 0 𝜕𝑔 𝑤 2 Τ𝜕𝑤22 =0 1 𝑇 2 𝑇 = 𝑤 𝑆𝑤 = 𝑤 2 𝑇 𝑆𝑇 𝑤1 … = 𝑤 2 𝑇 𝑆𝑤 1 = 𝜆1 𝑤 2 𝑇 𝑤 1 = 0 𝑆𝑤 1 = 𝜆1 𝑤 1 𝛽 = 0: 𝑆𝑤 2 − 𝛼𝑤 2 = 0 𝑆𝑤 2 = 𝛼𝑤 2 𝑤 2 is the eigenvector of the covariance matrix S Corresponding to the 2nd largest eigenvalue 𝜆2 

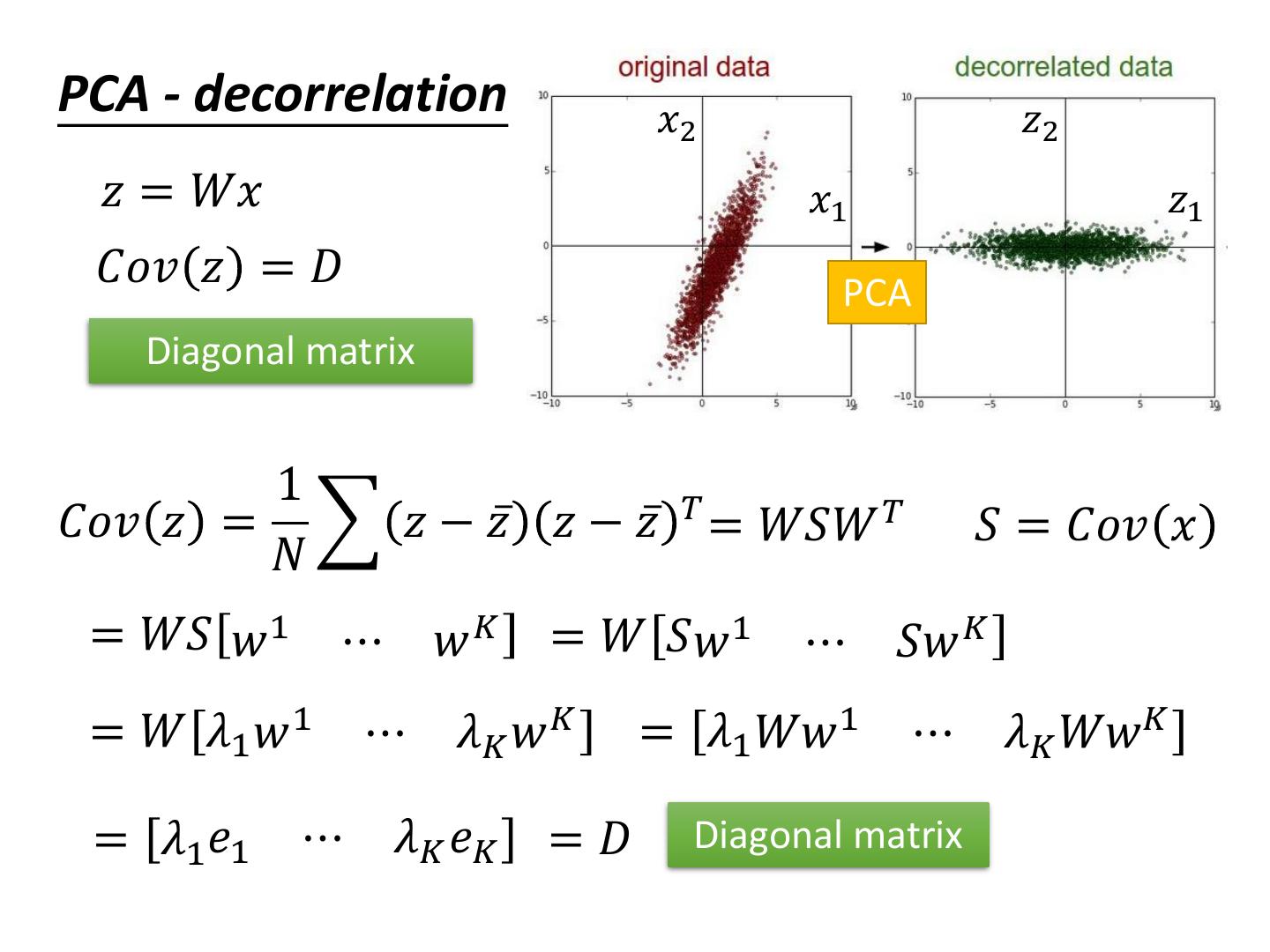
15 .PCA - decorrelation 𝑥2 𝑧2 𝑧 = 𝑊𝑥 𝑥1 𝑧1 𝐶𝑜𝑣 𝑧 = 𝐷 PCA Diagonal matrix 1 𝐶𝑜𝑣 𝑧 = ෍ 𝑧 − 𝑧ҧ 𝑧 − 𝑧ҧ 𝑇 = 𝑊𝑆𝑊 𝑇 𝑆 = 𝐶𝑜𝑣 𝑥 𝑁 = 𝑊𝑆 𝑤 1 ⋯ 𝑤𝐾 = 𝑊 𝑆𝑤 1 ⋯ 𝑆𝑤 𝐾 = 𝑊 𝜆1 𝑤 1 ⋯ 𝜆𝐾 𝑤 𝐾 = 𝜆1 𝑊𝑤 1 ⋯ 𝜆𝐾 𝑊𝑤𝐾 = 𝜆1 𝑒1 ⋯ 𝜆𝐾 𝑒𝐾 =𝐷 Diagonal matrix 

16 .End of Warning 

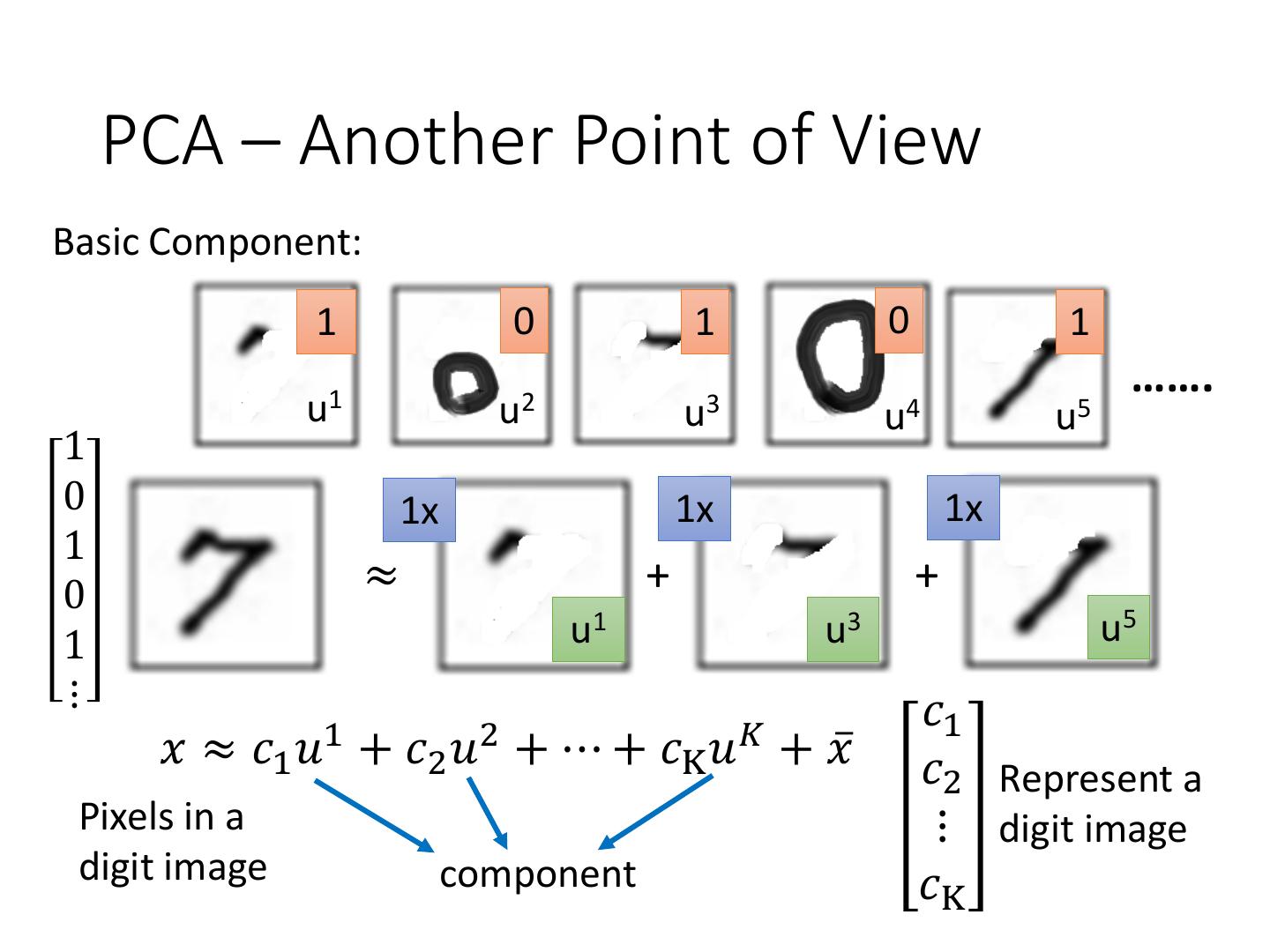
17 . PCA – Another Point of View Basic Component: 1 0 1 0 1 ……. u1 u2 u3 u4 u5 1 0 1x 1x 1x 1 0 ≈ + + 1 u1 u3 u5 ⋮ 𝑐1 1 2 𝐾 𝑥 ≈ 𝑐1 𝑢 + 𝑐2 𝑢 + ⋯ + 𝑐K 𝑢 + 𝑥ҧ 𝑐2 Represent a Pixels in a ⋮ digit image digit image component 𝑐K 

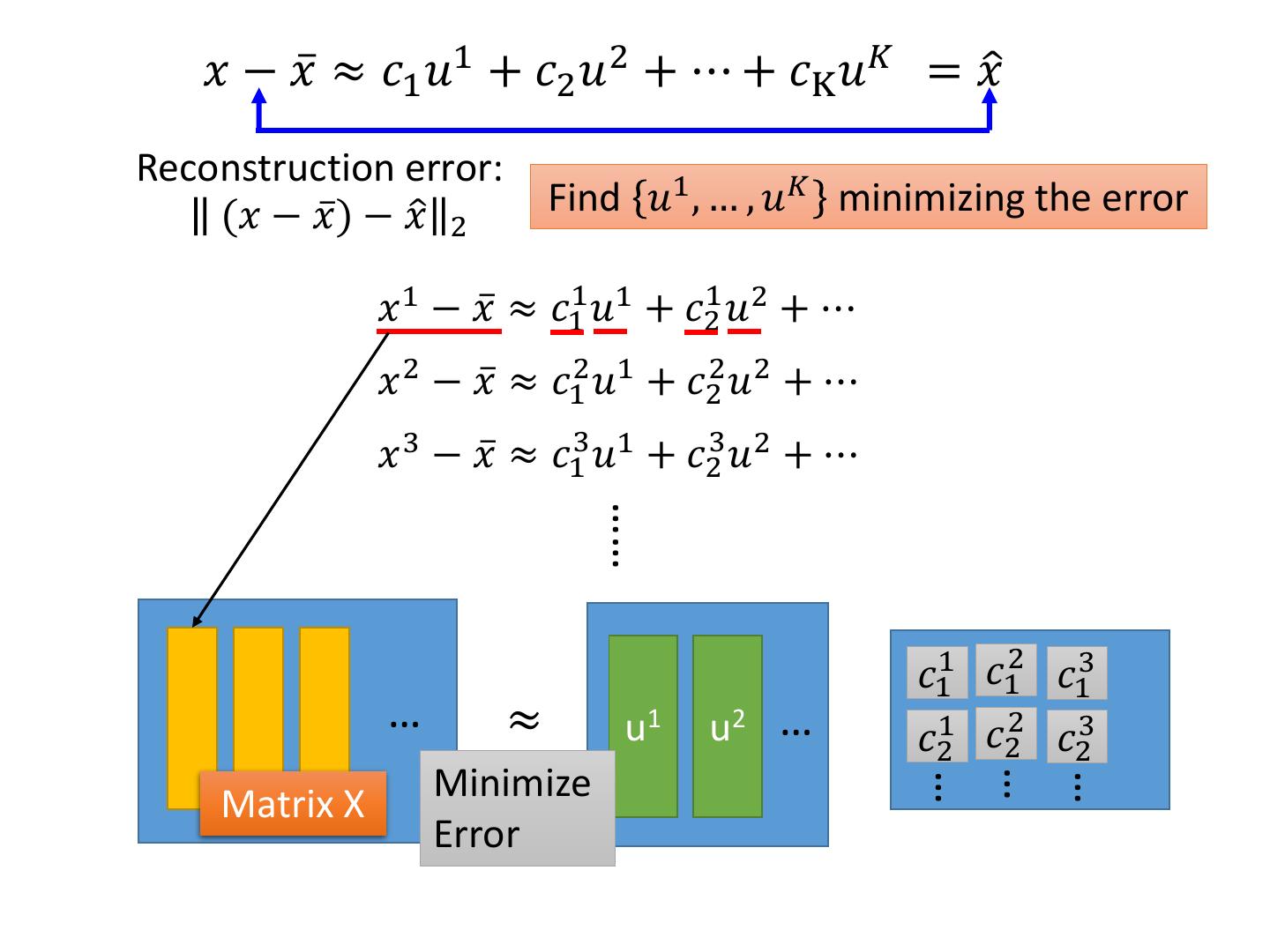
18 .PCA – Another Point of View 𝑥 − 𝑥ҧ ≈ 𝑐1 𝑢1 + 𝑐2 𝑢2 + ⋯ + 𝑐K 𝑢𝐾 = 𝑥ො Reconstruction error: (𝑥 − 𝑥)ҧ − 𝑥ො 2 Find 𝑢1 , … , 𝑢𝐾 minimizing the error 𝐾 𝐿= min𝐾 ෍ 1 𝑥 − 𝑥ҧ − ෍ 𝑐𝑘 𝑢𝑘 𝑢 ,…,𝑢 𝑘=1 2 PCA: 𝑧 = 𝑊𝑥 𝑥ො 𝑧1 T 𝑤1 𝑤 1 , 𝑤 2 , … 𝑤 𝐾 (from PCA) is the 𝑧2 𝑤2 T component 𝑢1 , 𝑢2 , … 𝑢𝐾 ⋮ = ⋮ 𝑥 minimizing L 𝑧𝐾 𝑤𝐾 T Proof in [Bishop, Chapter 12.1.2] 

19 . 𝑥 − 𝑥ҧ ≈ 𝑐1 𝑢1 + 𝑐2 𝑢2 + ⋯ + 𝑐K 𝑢𝐾 = 𝑥ො Reconstruction error: (𝑥 − 𝑥)ҧ − 𝑥ො 2 Find 𝑢1 , … , 𝑢𝐾 minimizing the error 𝑥 1 − 𝑥ҧ ≈ 𝑐11 𝑢1 + 𝑐21 𝑢2 + ⋯ 𝑥 2 − 𝑥ҧ ≈ 𝑐12 𝑢1 + 𝑐22 𝑢2 + ⋯ 𝑥 3 − 𝑥ҧ ≈ 𝑐13 𝑢1 + 𝑐23 𝑢2 + ⋯ …… 𝑐11 𝑐12 𝑐13 … ≈ u1 u2 … 𝑐21 𝑐22 𝑐23 Minimize … … … Matrix X Error 

20 . 𝑥 1 − 𝑥ҧ 𝑐11 𝑐12 𝑐13 … ≈ u1 u2 … 𝑐21 𝑐22 𝑐23 Minimize … … … Matrix X Error MxN MxK KxK KxN ∑ V X ≈ U K columns of U: a set of orthonormal eigen vectors corresponding to the K largest eigenvalues of XXT This is the solution of PCA SVD: http://speech.ee.ntu.edu.tw/~tlkagk/courses/LA_2016/Lecture/SVD.pdf 

21 . PCA looks like a neural network with one Autoencoder hidden layer (linear activation function) If 𝑤 1 , 𝑤 2 , … 𝑤 𝐾 is the component 𝑢1 , 𝑢2 , … 𝑢𝐾 𝐾 To minimize reconstruction error: 𝑥ො = ෍ 𝑐𝑘 𝑤 𝑘 𝑥 − 𝑥ҧ 𝑐𝑘 = 𝑥 − 𝑥ҧ ∙ 𝑤 𝑘 𝑘=1 𝐾 = 2: 𝑤11 𝑐1 𝑥 − 𝑥ҧ 𝑤21 𝑤31 

22 . PCA looks like a neural network with one Autoencoder hidden layer (linear activation function) If 𝑤 1 , 𝑤 2 , … 𝑤 𝐾 is the component 𝑢1 , 𝑢2 , … 𝑢𝐾 𝐾 To minimize reconstruction error: 𝑥ො = ෍ 𝑐𝑘 𝑤 𝑘 𝑥 − 𝑥ҧ 𝑐𝑘 = 𝑥 − 𝑥ҧ ∙ 𝑤 𝑘 𝑘=1 𝐾 = 2: 𝑐1 𝑥 − 𝑥ҧ 𝑤12 𝑐2 𝑤22 𝑤32 

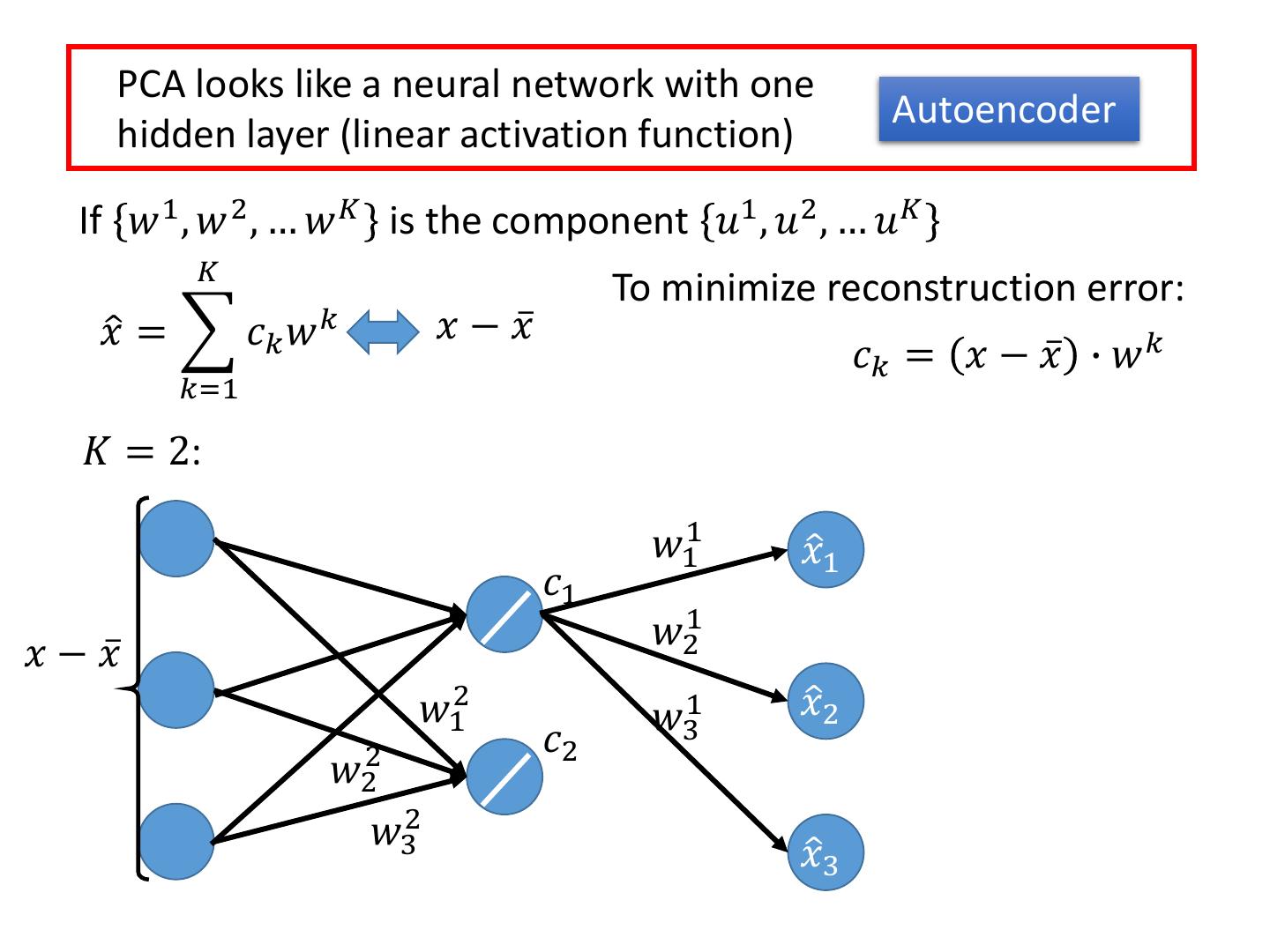
23 . PCA looks like a neural network with one Autoencoder hidden layer (linear activation function) If 𝑤 1 , 𝑤 2 , … 𝑤 𝐾 is the component 𝑢1 , 𝑢2 , … 𝑢𝐾 𝐾 To minimize reconstruction error: 𝑥ො = ෍ 𝑐𝑘 𝑤 𝑘 𝑥 − 𝑥ҧ 𝑐𝑘 = 𝑥 − 𝑥ҧ ∙ 𝑤 𝑘 𝑘=1 𝐾 = 2: 𝑤11 𝑥ො1 𝑐1 𝑤21 𝑥 − 𝑥ҧ 𝑤12 𝑤31 𝑥ො2 𝑐2 𝑤22 𝑤32 𝑥ො3 

24 . PCA looks like a neural network with one Autoencoder hidden layer (linear activation function) If 𝑤 1 , 𝑤 2 , … 𝑤 𝐾 is the component 𝑢1 , 𝑢2 , … 𝑢𝐾 𝐾 To minimize reconstruction error: 𝑥ො = ෍ 𝑐𝑘 𝑤 𝑘 𝑥 − 𝑥ҧ 𝑐𝑘 = 𝑥 − 𝑥ҧ ∙ 𝑤 𝑘 𝑘=1 𝐾 = 2: It can be deep. Deep Autoencoder 𝑥ො1 Minimize 𝑐1 𝑤12 error 𝑥 − 𝑥ҧ 𝑥 − 𝑥ҧ 𝑤12 𝑥ො2 𝑐2 𝑤22 𝑤22 Gradient 𝑤32 Descent? 𝑤32 𝑥ො3 

25 .PCA - Pokémon • Inspired from: https://www.kaggle.com/strakul5/d/abcsds/pokemon/princi pal-component-analysis-of-pokemon-data • 800 Pokemons, 6 features for each (HP, Atk, Def, Sp Atk, Sp Def, Speed) 𝜆𝑖 • How many principle components? 𝜆1 + 𝜆2 + 𝜆3 + 𝜆4 + 𝜆5 + 𝜆6 𝜆1 𝜆2 𝜆3 𝜆4 𝜆5 𝜆6 ratio 0.45 0.18 0.13 0.12 0.07 0.04 Using 4 components is good enough 

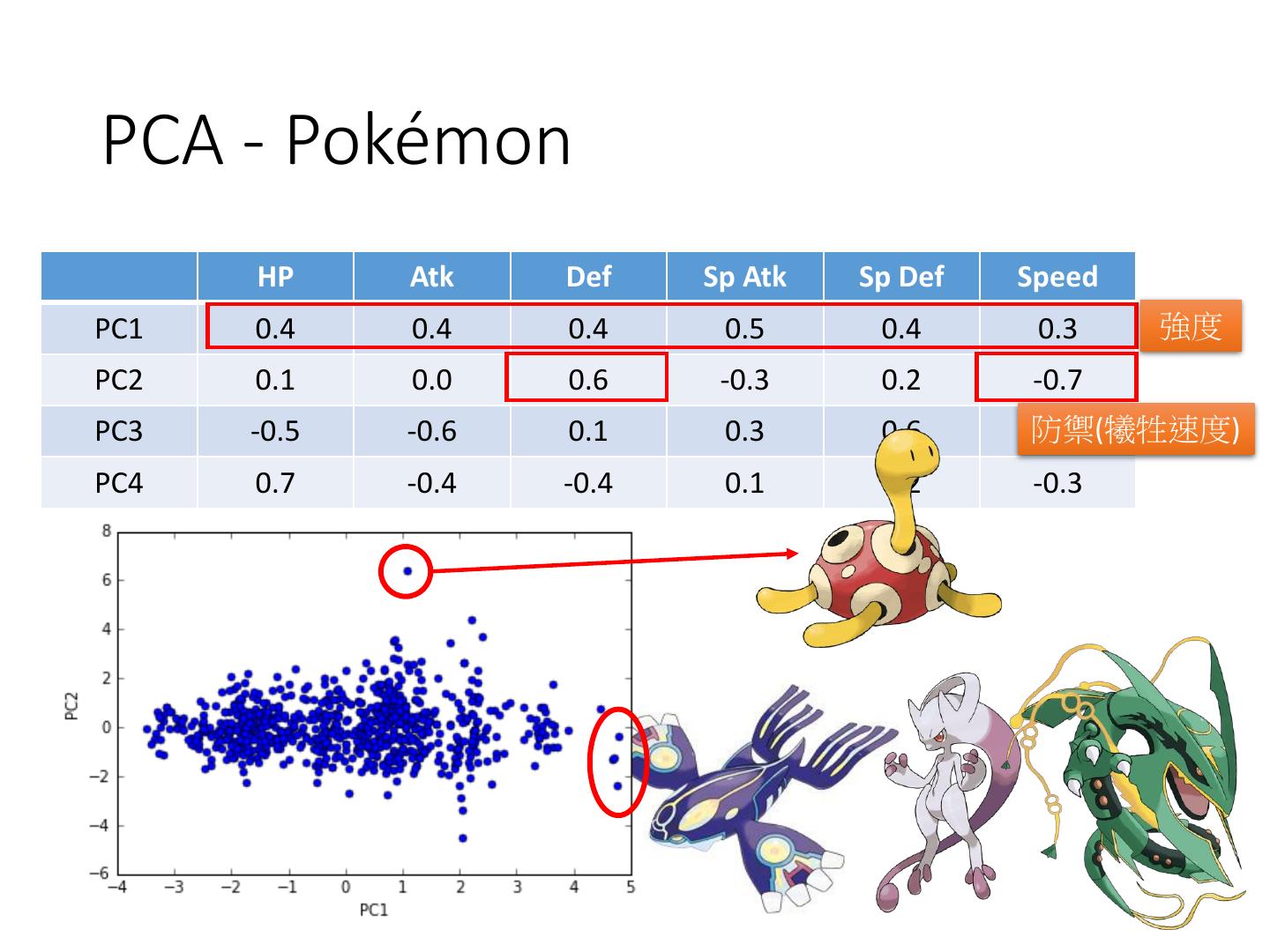
26 .PCA - Pokémon HP Atk Def Sp Atk Sp Def Speed PC1 0.4 0.4 0.4 0.5 0.4 0.3 強度 PC2 0.1 0.0 0.6 -0.3 0.2 -0.7 PC3 -0.5 -0.6 0.1 0.3 0.6 防禦(犧牲速度) 0.1 PC4 0.7 -0.4 -0.4 0.1 0.2 -0.3 

27 . PCA - Pokémon HP Atk Def Sp Atk Sp Def Speed PC1 0.4 0.4 0.4 0.5 0.4 0.3 PC2 0.1 0.0 0.6 -0.3 0.2 -0.7 PC3 -0.5 -0.6 0.1 0.3 0.6 特殊防禦(犧牲 0.1 生命力強 PC4 0.7 -0.4 -0.4 0.1 0.2 攻擊和生命) -0.3 

28 .PCA - Pokémon • http://140.112.21.35:2880/~tlkagk/pokemon/pca.html • The code is modified from • http://jkunst.com/r/pokemon-visualize-em-all/ 

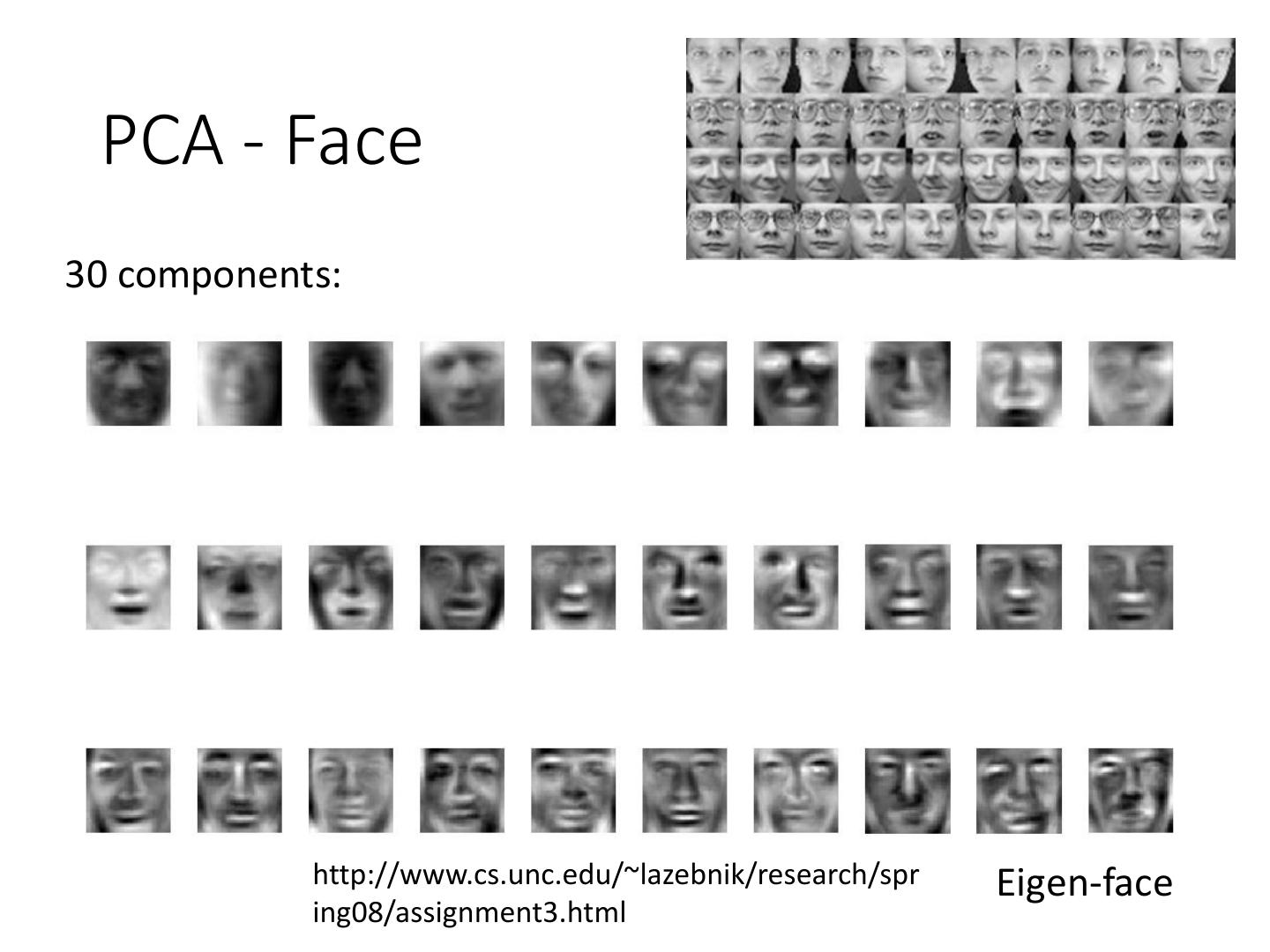
29 . PCA - MNIST = 𝑎1 𝑤 1 + 𝑎2 𝑤 2 + ⋯ images 30 components: Eigen-digits