Matrix Factorization

1 .Matrix Factorization 

2 .Otakus v.s. No. of Figures A 5 3 0 1 B 4 3 0 1 C 1 1 0 5 D 1 0 4 4 E 0 1 5 4 There are some common factors behind otakus and characters. http://www.quuxlabs.com/blog/2010/09/matrix-factorization-a-simple-tutorial-and- implementation-in-python/ 

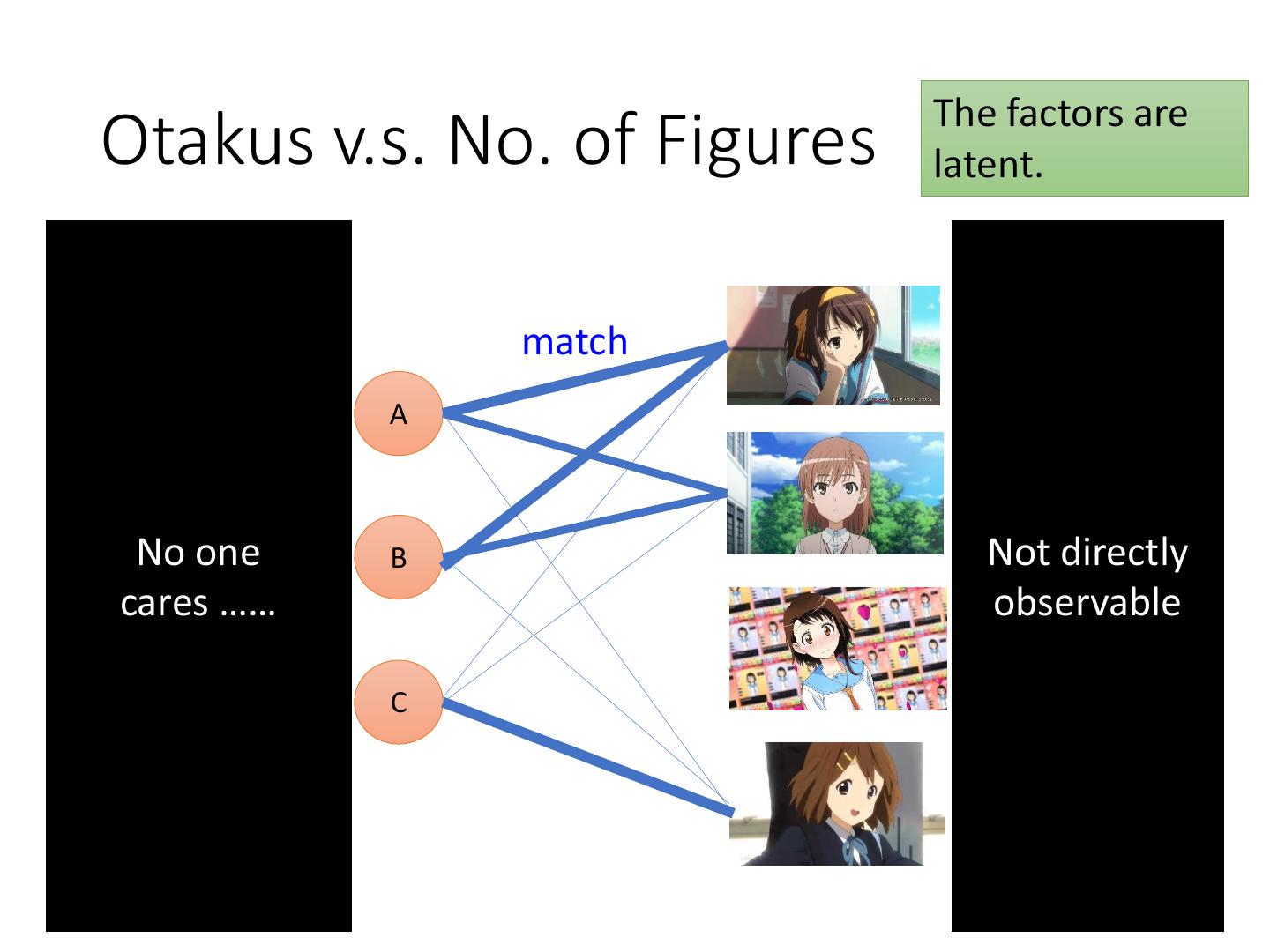
3 . The factors are Otakus v.s. No. of Figures latent. 呆 呆 match 傲 傲 A 呆 呆 No one B 傲 Not directly cares …… 呆observable 傲 呆 C 傲 呆 傲 傲 

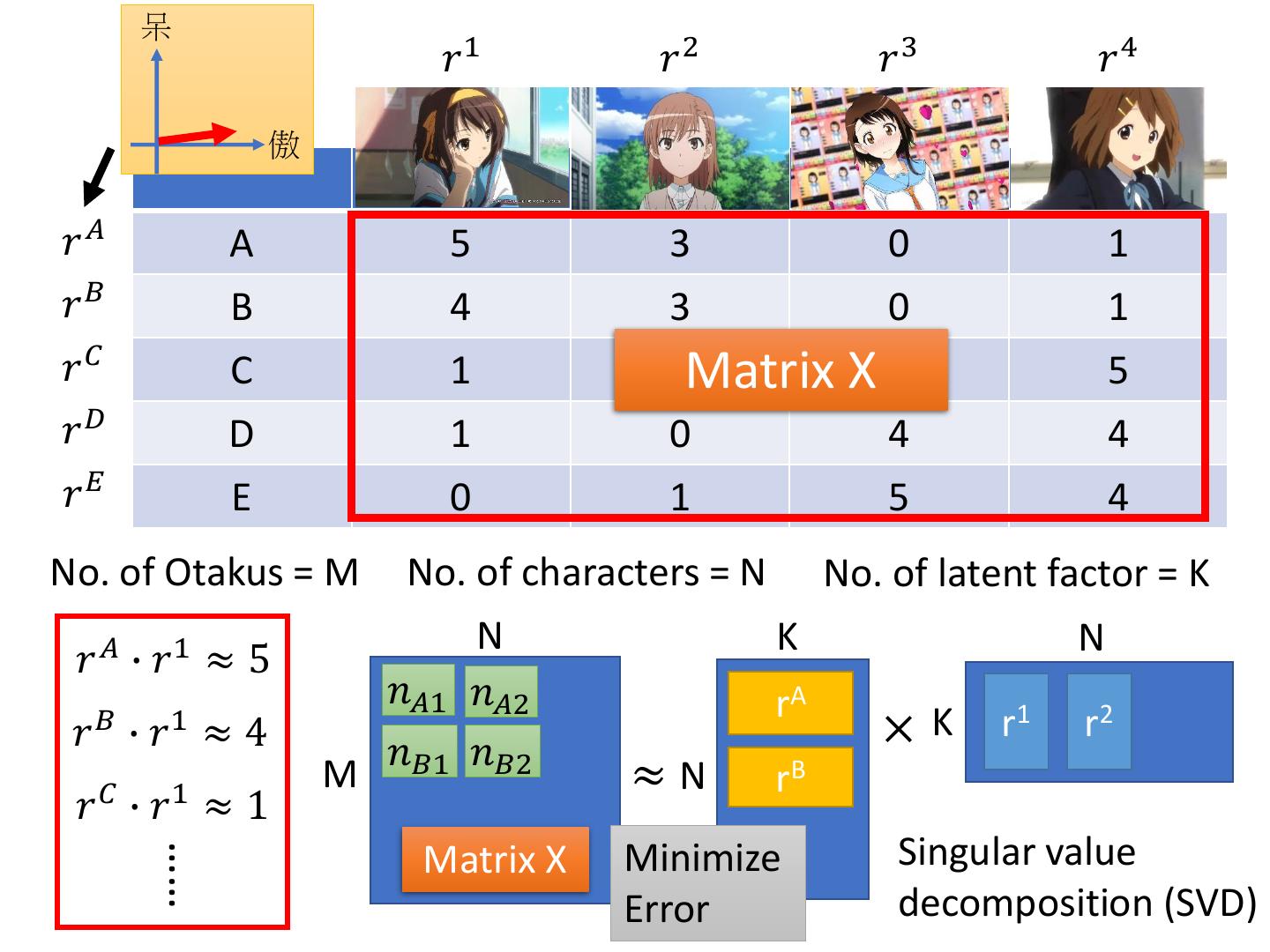
4 . 呆 𝑟1 𝑟2 𝑟3 𝑟4 傲 𝑟𝐴 A 5 3 0 1 𝑟𝐵 B 4 3 0 1 𝑟𝐶 C 1 1Matrix X0 5 𝑟𝐷 D 1 0 4 4 𝑟𝐸 E 0 1 5 4 No. of Otakus = M No. of characters = N No. of latent factor = K N K N 𝑟 𝐴 ∙ 𝑟1 ≈ 5 𝑛𝐴1 𝑛𝐴2 rA 𝑟 𝐵 ∙ 𝑟1 ≈ 4 𝑛 𝑛 × K r1 r2 M 𝐵1 𝐵2 ≈ N rB 𝑟 𝐶 ∙ 𝑟1 ≈ 1 Minimize Singular value …… Matrix X Error decomposition (SVD) 

5 . 𝑟𝑗 𝑟1 𝑟2 𝑟3 𝑟4 𝑟𝑖 𝑟𝐴 A 5 𝑛𝐴1 3 ? 1 𝑟𝐵 B 4 3 ? 1 𝑟𝐶 C 1 1 ? 5 𝑟𝐷 D 1 ? 4 4 𝑟𝐸 E ? 1 5 4 𝐴 1 Only considering the 𝑟 ∙𝑟 ≈5 Minimizing defined value 𝑟 𝐵 ∙ 𝑟1 ≈ 4 2 𝐿=෍ 𝑟𝑖 ∙ 𝑟𝑗 − 𝑛𝑖𝑗 𝑟𝐶 ∙ 𝑟1 ≈1 𝑖,𝑗 …… Find 𝑟 𝑖 and 𝑟 𝑗 by gradient descent 

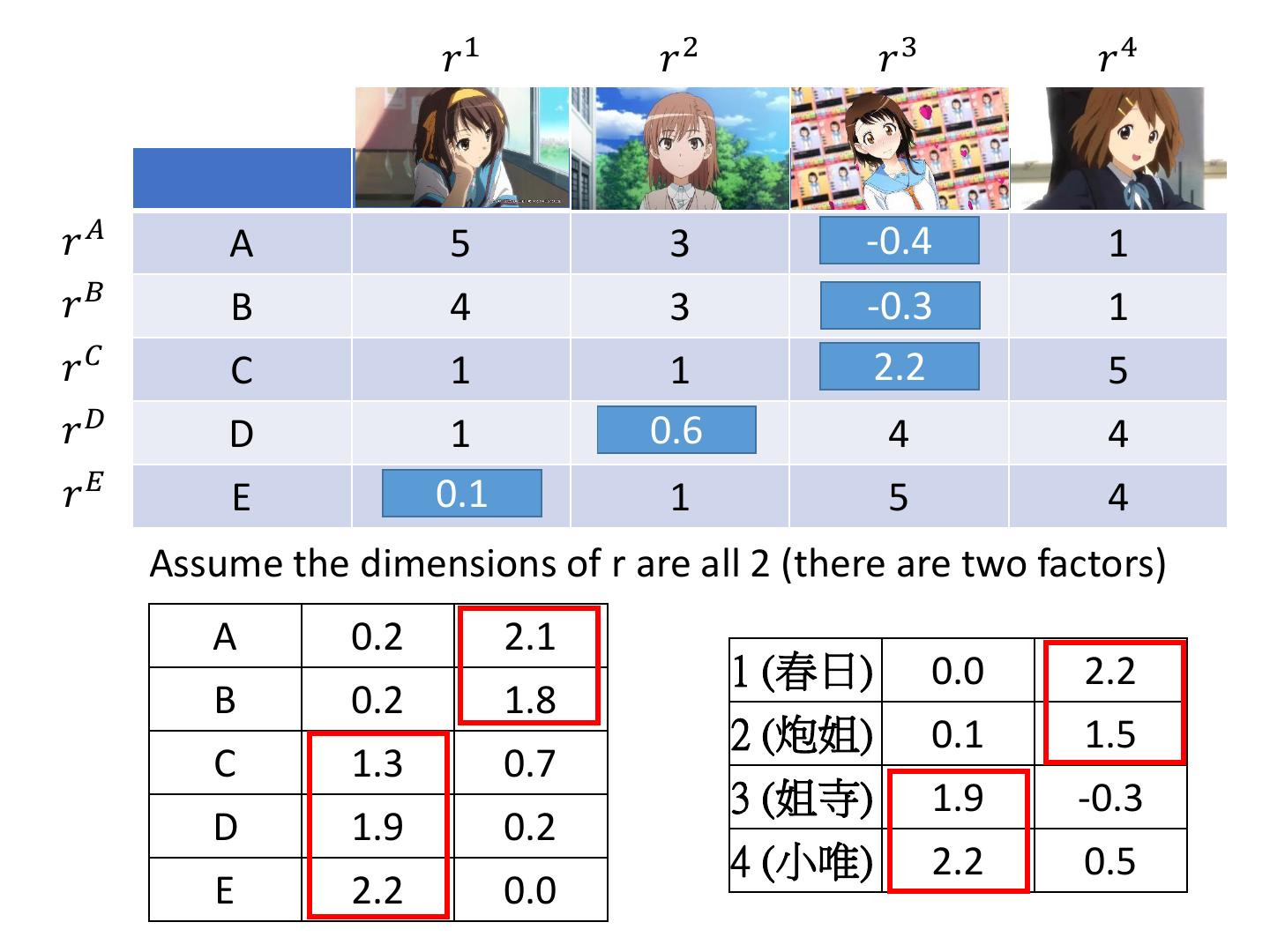
6 . 𝑟1 𝑟2 𝑟3 𝑟4 𝑟𝐴 A 5 3 -0.4 ? 1 𝑟𝐵 B 4 3 -0.3 ? 1 𝑟𝐶 C 1 1 2.2 ? 5 𝑟𝐷 D 1 0.6 ? 4 4 𝑟𝐸 E 0.1 ? 1 5 4 Assume the dimensions of r are all 2 (there are two factors) A 0.2 2.1 1 (春日) 0.0 2.2 B 0.2 1.8 2 (炮姐) 0.1 1.5 C 1.3 0.7 3 (姐寺) 1.9 -0.3 D 1.9 0.2 4 (小唯) 2.2 0.5 E 2.2 0.0 

7 .More about Matrix Factorization • Considering the induvial characteristics 𝑟 𝐴 ∙ 𝑟1 ≈ 5 𝑟 𝐴 ∙ 𝑟1 + 𝑏𝐴 + 𝑏1 ≈ 5 𝑏𝐴 : otakus A likes to buy figures 𝑏1 : how popular character 1 is 2 Minimizing 𝐿=෍ 𝑟𝑖 ∙ 𝑟𝑗 + 𝑏𝑖 + 𝑏𝑗 − 𝑛𝑖𝑗 𝑖,𝑗 Find 𝑟 𝑖 , 𝑟 𝑗 , 𝑏𝑖 , 𝑏𝑗 by gradient descent (can add regularization) • Ref: Matrix Factorization Techniques For Recommender Systems 

8 .Matrix Factorization for Topic analysis character→document, otakus→word • Latent semantic analysis (LSA) Number in Table: Doc 1 Doc 2 Doc 3 Doc 4 Term frequency 投資 5 3 0 1 (weighted by inverse 股票 4 0 0 1 document frequency) 總統 1 1 0 5 選舉 1 0 0 4 Latent factors are topics 立委 0 1 5 4 (財經、政治 …… ) • Probability latent semantic analysis (PLSA) • Thomas Hofmann, Probabilistic Latent Semantic Indexing, SIGIR, 1999 • latent Dirichlet allocation (LDA) • David M. Blei, Andrew Y. Ng, Michael I. Jordan, Latent Dirichlet Allocation, Journal of Machine Learning Research, 2003