Logistic Regression

1 . Classification: Logistic Regression Hung-yi Lee 李宏毅 

2 .有關分組 • 作業以個人為單位繳交 • 期末專題才需要分組 • 找不到組員也沒有關係，期末專題公告後找不到 組員的同學助教會幫忙湊對 

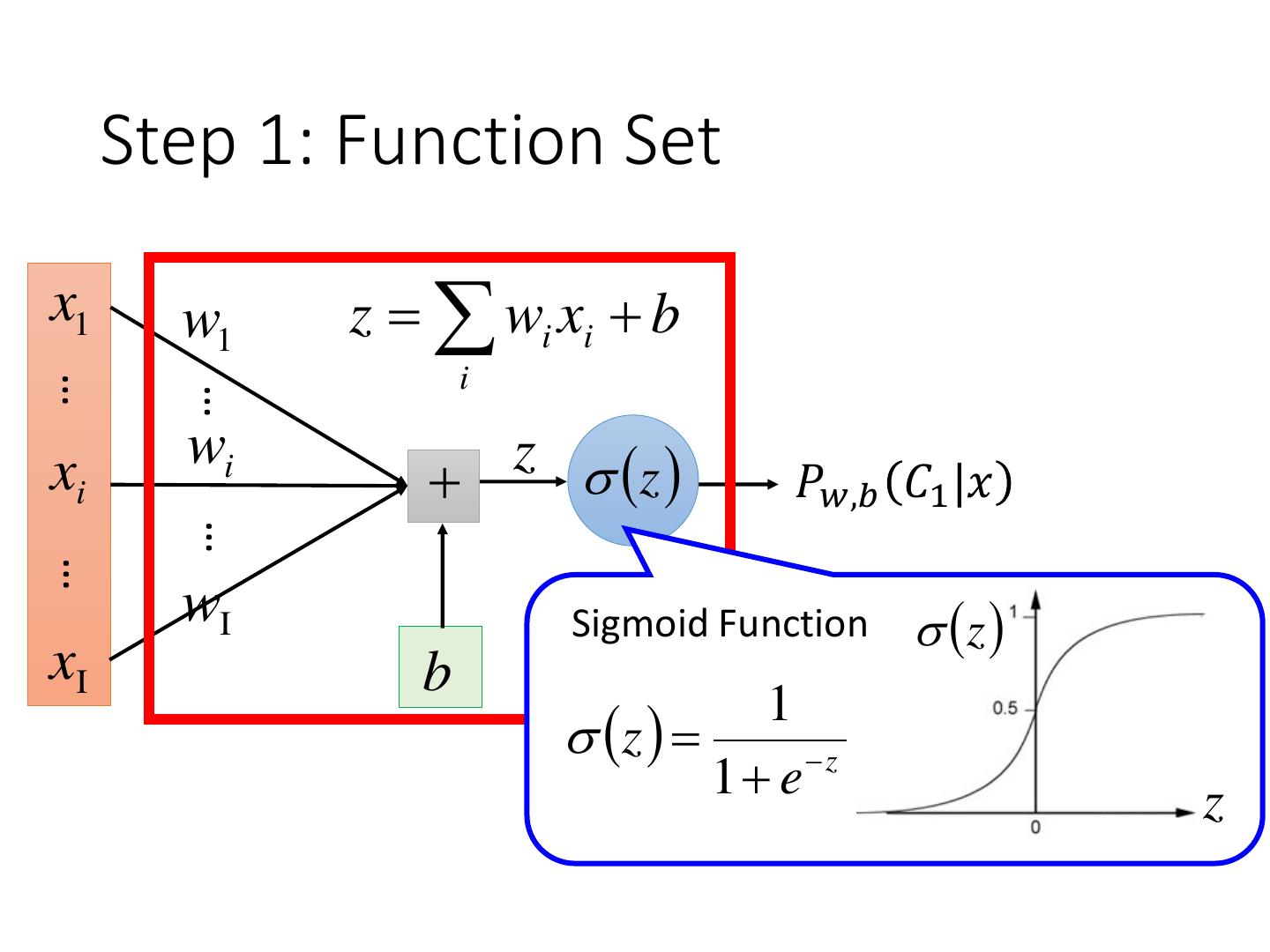
3 .Step 1: Function Set Function set: Including all different w and b 𝑃𝑤,𝑏 z𝐶1 |𝑥 ≥ 0.5 0 class 1 𝑃𝑤,𝑏 z𝐶1 |𝑥 < 0.5 0 class 2 𝑃𝑤,𝑏 𝐶1 |𝑥 = 𝜎 𝑧  z  𝑧 = 𝑤 ∙ 𝑥 + 𝑏 = ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑖 1 𝜎 𝑧 = 1 + 𝑒𝑥𝑝 −𝑧 z 

4 . Step 1: Function Set x1 w1 z   wi xi  b i … … wi z  z  xi  𝑃𝑤,𝑏 𝐶1 |𝑥 … … wI Sigmoid Function  z  xI b  z   1 1  ez z 

5 .Step 2: Goodness of a Function Training 𝑥1 𝑥2 𝑥3 𝑥𝑁 …… Data 𝐶1 𝐶1 𝐶2 𝐶1 Assume the data is generated based on 𝑓𝑤,𝑏 𝑥 = 𝑃𝑤,𝑏 𝐶1 |𝑥 Given a set of w and b, what is its probability of generating the data? 𝐿 𝑤, 𝑏 = 𝑓𝑤,𝑏 𝑥 1 𝑓𝑤,𝑏 𝑥 2 1 − 𝑓𝑤,𝑏 𝑥 3 ⋯ 𝑓𝑤,𝑏 𝑥 𝑁 The most likely w* and b* is the one with the largest 𝐿 𝑤, 𝑏 . 𝑤 ∗ , 𝑏 ∗ = 𝑎𝑟𝑔 max 𝐿 𝑤, 𝑏 𝑤,𝑏 

6 . 𝑥1 𝑥2 𝑥3 𝑥1 𝑥2 𝑥3 …… …… 3 𝐶1 𝐶1 𝐶2 𝑦ො 1 =1 𝑦ො 2 = 1 𝑦ො = 0 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 𝐿 𝑤, 𝑏 = 𝑓𝑤,𝑏 𝑥 1 𝑓𝑤,𝑏 𝑥 2 1 − 𝑓𝑤,𝑏 𝑥 3 ⋯ 𝑤 ∗ , 𝑏 ∗ = 𝑎𝑟𝑔 max 𝐿 𝑤, 𝑏 𝑤,𝑏 = 𝑤 ∗ , 𝑏 ∗ = 𝑎𝑟𝑔 min 𝑤,𝑏 −𝑙𝑛𝐿 𝑤, 𝑏 −𝑙𝑛𝐿 𝑤, 𝑏 = −𝑙𝑛𝑓𝑤,𝑏 𝑥 1 − 𝑦ො11 𝑙𝑛𝑓 𝑥 1 + 1 −0 𝑦ො 1 𝑙𝑛 1 − 𝑓 𝑥 1 −𝑙𝑛𝑓𝑤,𝑏 𝑥 2 − 𝑦ො12 𝑙𝑛𝑓 𝑥 2 + 1 −0 𝑦ො 2 𝑙𝑛 1 − 𝑓 𝑥 2 −𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 3 − 𝑦ො03 𝑙𝑛𝑓 𝑥 3 + 1 −1 𝑦ො 3 𝑙𝑛 1 − 𝑓 𝑥 3 …… 

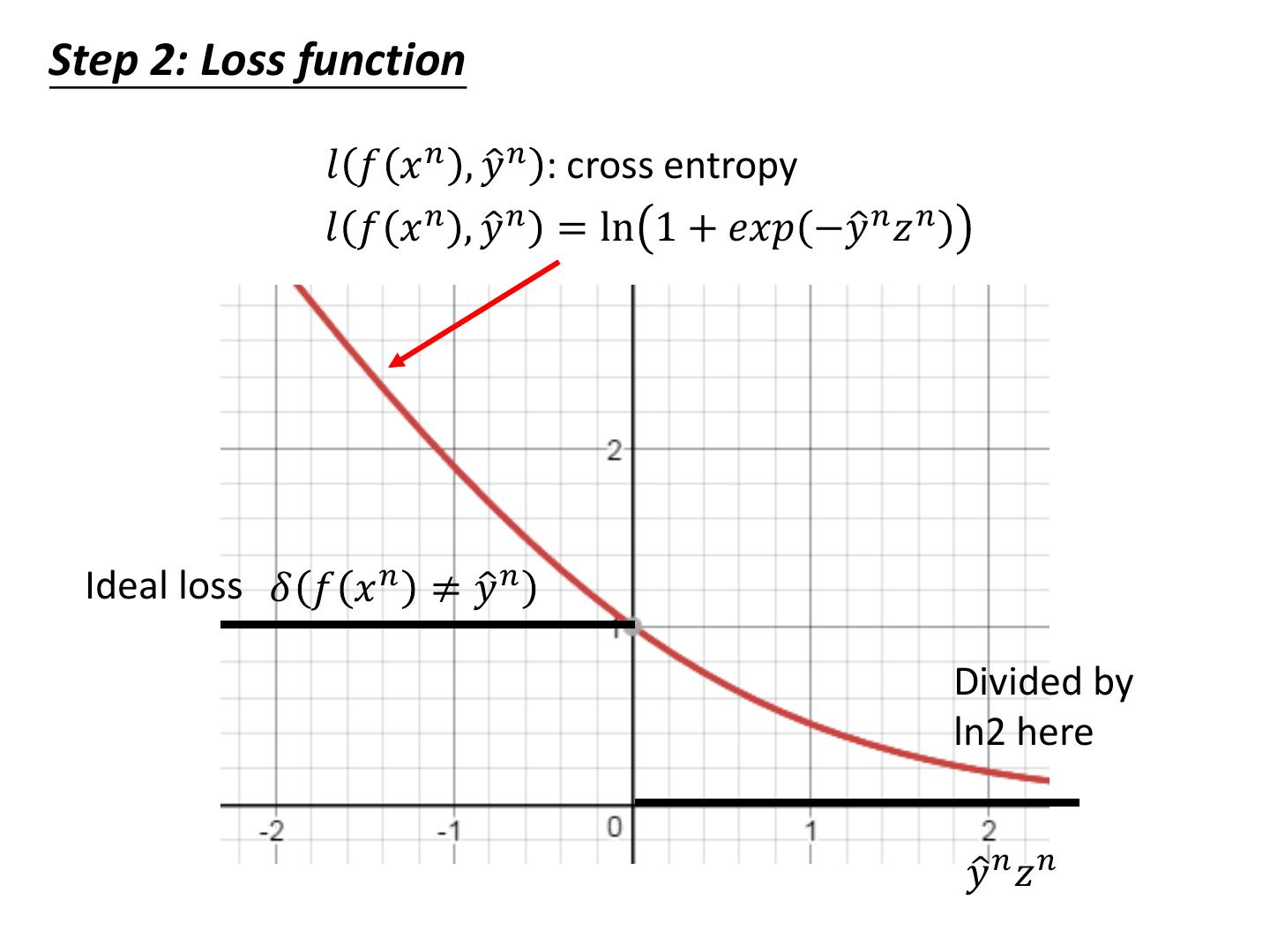
7 .Step 2: Goodness of a Function 𝐿 𝑤, 𝑏 = 𝑓𝑤,𝑏 𝑥 1 𝑓𝑤,𝑏 𝑥 2 1 − 𝑓𝑤,𝑏 𝑥 3 ⋯ 𝑓𝑤,𝑏 𝑥 𝑁 −𝑙𝑛𝐿 𝑤, 𝑏 = 𝑙𝑛𝑓𝑤,𝑏 𝑥 1 + 𝑙𝑛𝑓𝑤,𝑏 𝑥 2 + 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 3 ⋯ 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 = ෍ − 𝑦ො 𝑛 𝑙𝑛𝑓𝑤,𝑏 𝑥 𝑛 + 1 − 𝑦ො 𝑛 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑛 Cross entropy between two Bernoulli distribution Distribution p: Distribution q: p 𝑥 = 1 = 𝑦ො 𝑛 cross q 𝑥 = 1 = 𝑓 𝑥𝑛 p 𝑥 = 0 = 1 − 𝑦ො 𝑛 entropy q 𝑥 = 0 = 1 − 𝑓 𝑥𝑛 𝐻 𝑝, 𝑞 = − ෍ 𝑝 𝑥 𝑙𝑛 𝑞 𝑥 𝑥 

8 .Step 2: Goodness of a Function 𝐿 𝑤, 𝑏 = 𝑓𝑤,𝑏 𝑥 1 𝑓𝑤,𝑏 𝑥 2 1 − 𝑓𝑤,𝑏 𝑥 3 ⋯ 𝑓𝑤,𝑏 𝑥 𝑁 −𝑙𝑛𝐿 𝑤, 𝑏 = 𝑙𝑛𝑓𝑤,𝑏 𝑥 1 + 𝑙𝑛𝑓𝑤,𝑏 𝑥 2 + 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 3 ⋯ 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 = ෍ − 𝑦ො 𝑛 𝑙𝑛𝑓𝑤,𝑏 𝑥 𝑛 + 1 − 𝑦ො 𝑛 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑛 Cross entropy between two Bernoulli distribution minimize 1.0 𝑓 𝑥𝑛 0.0 cross 1 − 𝑓 𝑥𝑛 Ground Truth entropy 𝑦ො 𝑛 = 1 

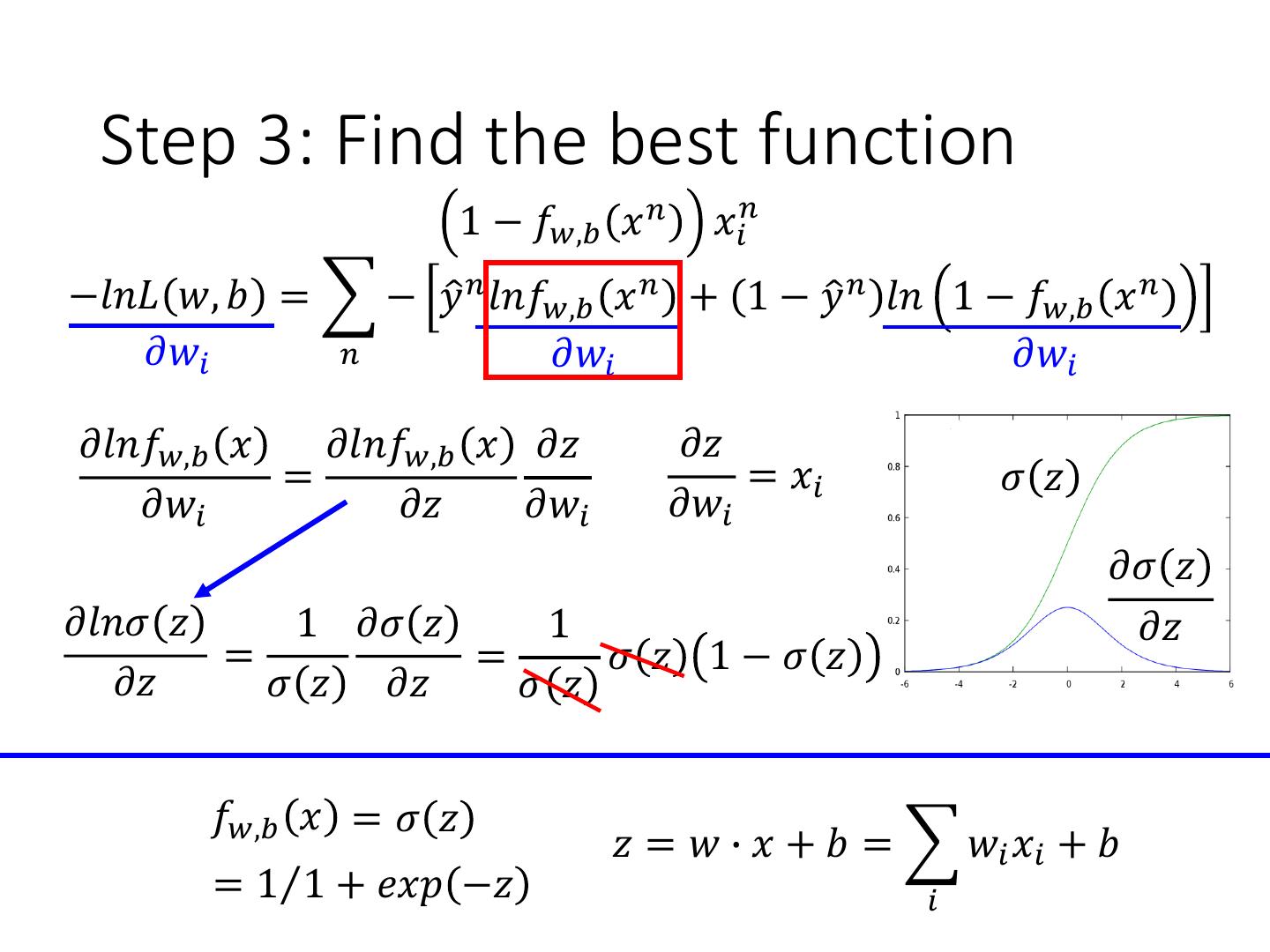
9 . Step 3: Find the best function 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 −𝑙𝑛𝐿 𝑤, 𝑏 = ෍ − 𝑦ො 𝑛 𝑙𝑛𝑓𝑤,𝑏 𝑥 𝑛 + 1 − 𝑦ො 𝑛 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝜕𝑤𝑖 𝑛 𝜕𝑤𝑖 𝜕𝑤𝑖 𝜕𝑙𝑛𝑓𝑤,𝑏 𝑥 𝜕𝑙𝑛𝑓𝑤,𝑏 𝑥 𝜕𝑧 𝜕𝑧 = = 𝑥𝑖 𝜎 𝑧 𝜕𝑤𝑖 𝜕𝑧 𝜕𝑤𝑖 𝜕𝑤𝑖 𝜕𝜎 𝑧 𝜕𝑙𝑛𝜎 𝑧 1 𝜕𝜎 𝑧 1 𝜕𝑧 = = 𝜎 𝑧 1−𝜎 𝑧 𝜕𝑧 𝜎 𝑧 𝜕𝑧 𝜎 𝑧 𝑓𝑤,𝑏 𝑥 = 𝜎 𝑧 𝑧 = 𝑤 ∙ 𝑥 + 𝑏 = ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 = 1Τ1 + 𝑒𝑥𝑝 −𝑧 𝑖 

10 . Step 3: Find the best function 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 −𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 −𝑙𝑛𝐿 𝑤, 𝑏 = ෍ − 𝑦ො 𝑛 𝑙𝑛𝑓𝑤,𝑏 𝑥 𝑛 + 1 − 𝑦ො 𝑛 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝜕𝑤𝑖 𝑛 𝜕𝑤𝑖 𝜕𝑤𝑖 𝜕𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝜕𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝜕𝑧 𝜕𝑧 = = 𝑥𝑖 𝜕𝑤𝑖 𝜕𝑧 𝜕𝑤𝑖 𝜕𝑤𝑖 𝜕𝑙𝑛 1 − 𝜎 𝑧 1 𝜕𝜎 𝑧 1 =− =− 𝜎 𝑧 1−𝜎 𝑧 𝜕𝑧 1 − 𝜎 𝑧 𝜕𝑧 1−𝜎 𝑧 𝑓𝑤,𝑏 𝑥 = 𝜎 𝑧 𝑧 = 𝑤 ∙ 𝑥 + 𝑏 = ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 = 1Τ1 + 𝑒𝑥𝑝 −𝑧 𝑖 

11 . Step 3: Find the best function 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 −𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 −𝑙𝑛𝐿 𝑤, 𝑏 = ෍ − 𝑦ො 𝑛 𝑙𝑛𝑓𝑤,𝑏 𝑥 𝑛 + 1 − 𝑦ො 𝑛 𝑙𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝜕𝑤𝑖 𝑛 𝜕𝑤𝑖 𝜕𝑤𝑖 = ෍ − 𝑦ො 𝑛 1 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 − 1 − 𝑦ො 𝑛 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 𝑛 = ෍ − 𝑦ො 𝑛 − 𝑦ො 𝑛 𝑓𝑤,𝑏 𝑥 𝑛 − 𝑓𝑤,𝑏 𝑥 𝑛 + 𝑦ො 𝑛 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 𝑛 = ෍ − 𝑦ො 𝑛 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 Larger difference, larger update 𝑛 𝑤𝑖 ← 𝑤𝑖 − 𝜂 ෍ − 𝑦ො 𝑛 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 𝑛 

12 . Logistic Regression + Square Error Step 1: 𝑓𝑤,𝑏 𝑥 = 𝜎 ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑖 Step 2: Training data: 𝑥 𝑛 , 𝑦ො 𝑛 , 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 1 2 𝐿 𝑓 = ෍ 𝑓𝑤,𝑏 𝑥 𝑛 − 𝑦ො 𝑛 2 𝑛 Step 3: 𝜕𝑓𝑤,𝑏 𝑥 𝜕𝑧 = 2 𝑓𝑤,𝑏 𝑥 − 𝑦ො 𝜕 (𝑓𝑤,𝑏 ො 2 (𝑥)−𝑦) 𝜕𝑧 𝜕𝑤𝑖 𝜕𝑤𝑖 = 2 𝑓𝑤,𝑏 𝑥 − 𝑦ො 𝑓𝑤,𝑏 𝑥 1 − 𝑓𝑤,𝑏 𝑥 𝑥𝑖 𝑦ො 𝑛 = 1 If 𝑓𝑤,𝑏 𝑥 𝑛 = 1 (close to target) 𝜕𝐿Τ𝜕𝑤𝑖 = 0 If 𝑓𝑤,𝑏 𝑥 𝑛 = 0 (far from target) 𝜕𝐿Τ𝜕𝑤𝑖 = 0 

13 . Logistic Regression + Square Error Step 1: 𝑓𝑤,𝑏 𝑥 = 𝜎 ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑖 Step 2: Training data: 𝑥 𝑛 , 𝑦ො 𝑛 , 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 1 2 𝐿 𝑓 = ෍ 𝑓𝑤,𝑏 𝑥 𝑛 − 𝑦ො 𝑛 2 𝑛 Step 3: 𝜕𝑓𝑤,𝑏 𝑥 𝜕𝑧 = 2 𝑓𝑤,𝑏 𝑥 − 𝑦ො 𝜕 (𝑓𝑤,𝑏 ො 2 (𝑥)−𝑦) 𝜕𝑧 𝜕𝑤𝑖 𝜕𝑤𝑖 = 2 𝑓𝑤,𝑏 𝑥 − 𝑦ො 𝑓𝑤,𝑏 𝑥 1 − 𝑓𝑤,𝑏 𝑥 𝑥𝑖 𝑦ො 𝑛 = 0 If 𝑓𝑤,𝑏 𝑥 𝑛 = 1 (far from target) 𝜕𝐿Τ𝜕𝑤𝑖 = 0 If 𝑓𝑤,𝑏 𝑥 𝑛 = 0 (close to target) 𝜕𝐿Τ𝜕𝑤𝑖 = 0 

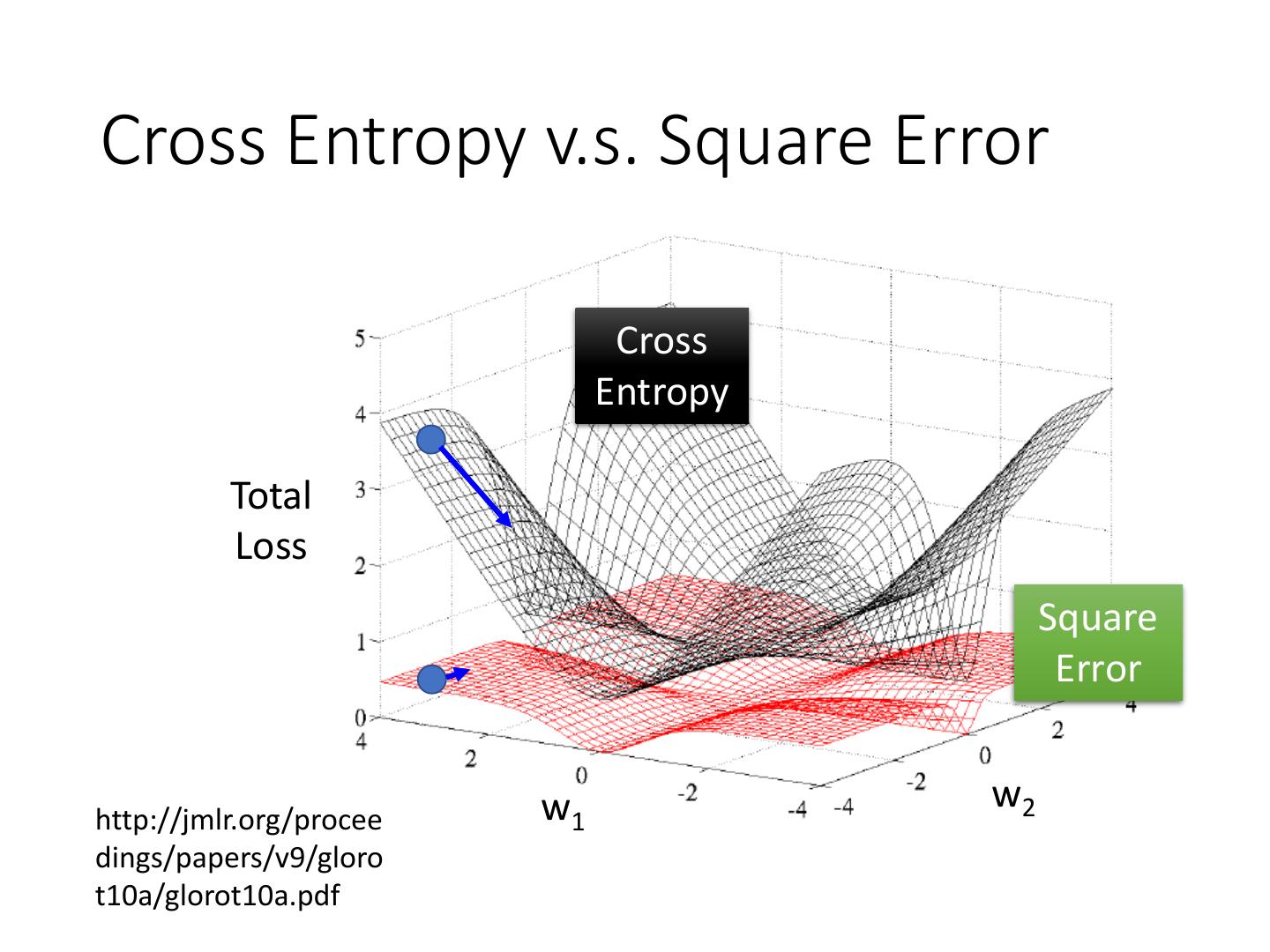
14 .Cross Entropy v.s. Square Error Cross Entropy Total Loss Square Error w1 w2 http://jmlr.org/procee dings/papers/v9/gloro t10a/glorot10a.pdf 

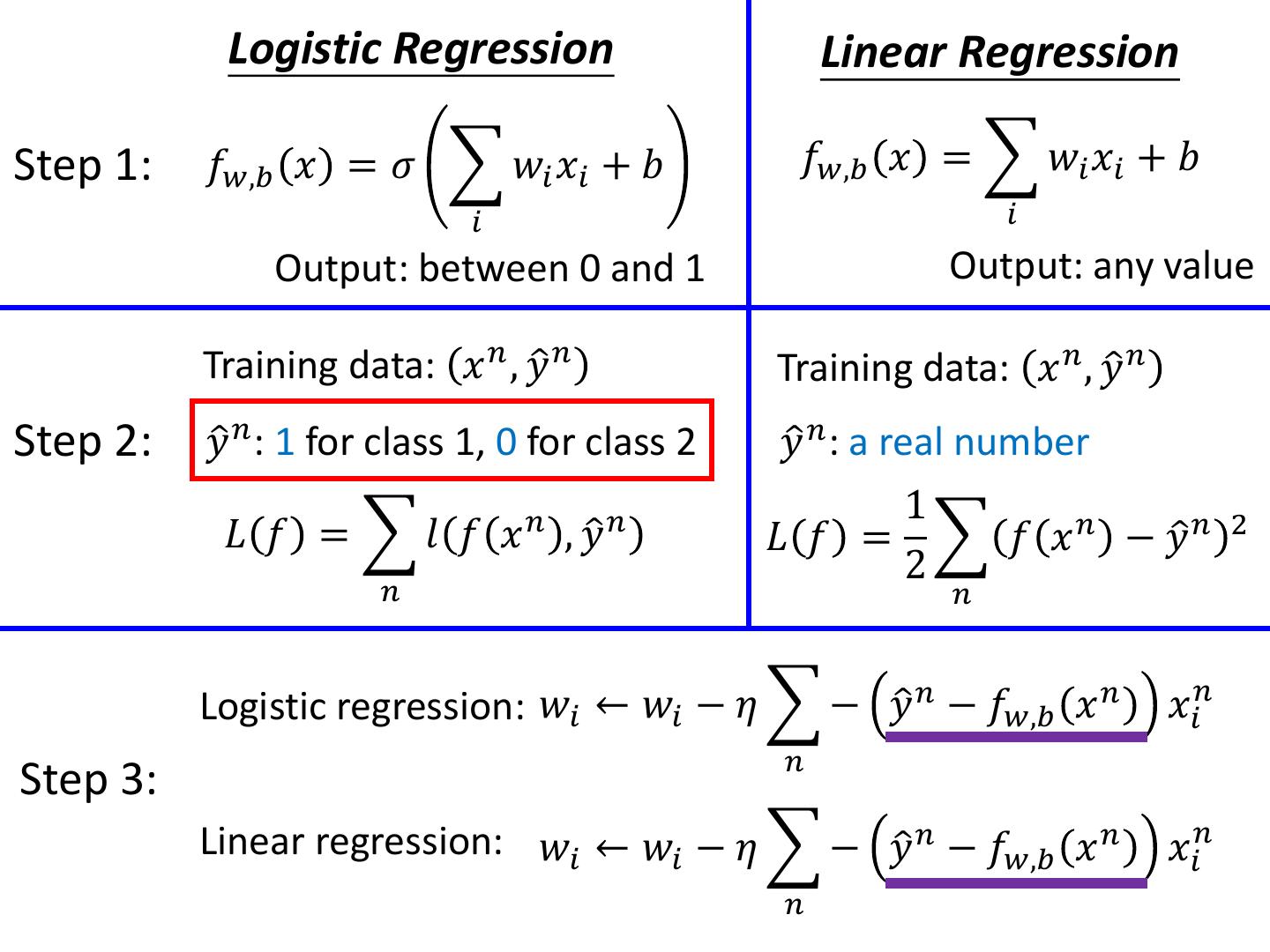
15 . Logistic Regression Linear Regression Step 1: 𝑓𝑤,𝑏 𝑥 = 𝜎 ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑓𝑤,𝑏 𝑥 = ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑖 𝑖 Output: between 0 and 1 Output: any value Step 2: Step 3: 

16 . Logistic Regression Linear Regression Step 1: 𝑓𝑤,𝑏 𝑥 = 𝜎 ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑓𝑤,𝑏 𝑥 = ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑖 𝑖 Output: between 0 and 1 Output: any value Training data: 𝑥 𝑛 , 𝑦ො 𝑛 Training data: 𝑥 𝑛 , 𝑦ො 𝑛 Step 2: 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 𝑦ො 𝑛 : a real number 1 𝐿 𝑓 = ෍ 𝑙 𝑓 𝑥 𝑛 , 𝑦ො 𝑛 𝐿 𝑓 = ෍ 𝑓 𝑥 𝑛 − 𝑦ො 𝑛 2 2 𝑛 𝑛 Cross entropy: 𝑙 𝑓 𝑥 𝑛 , 𝑦ො 𝑛 = − 𝑦ො 𝑛 𝑙𝑛𝑓 𝑥 𝑛 + 1 − 𝑦ො 𝑛 𝑙𝑛 1 − 𝑓 𝑥 𝑛 

17 . Logistic Regression Linear Regression Step 1: 𝑓𝑤,𝑏 𝑥 = 𝜎 ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑓𝑤,𝑏 𝑥 = ෍ 𝑤𝑖 𝑥𝑖 + 𝑏 𝑖 𝑖 Output: between 0 and 1 Output: any value Training data: 𝑥 𝑛 , 𝑦ො 𝑛 Training data: 𝑥 𝑛 , 𝑦ො 𝑛 Step 2: 𝑦ො 𝑛 : 1 for class 1, 0 for class 2 𝑦ො 𝑛 : a real number 1 𝐿 𝑓 = ෍ 𝑙 𝑓 𝑥 𝑛 , 𝑦ො 𝑛 𝐿 𝑓 = ෍ 𝑓 𝑥 𝑛 − 𝑦ො 𝑛 2 2 𝑛 𝑛 Logistic regression: 𝑤𝑖 ← 𝑤𝑖 − 𝜂 ෍ − 𝑦ො 𝑛 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 𝑛 Step 3: Linear regression: 𝑤𝑖 ← 𝑤𝑖 − 𝜂 ෍ − 𝑦ො 𝑛 − 𝑓𝑤,𝑏 𝑥 𝑛 𝑥𝑖𝑛 𝑛 

18 .Discriminative v.s. Generative 𝑃 𝐶1 |𝑥 = 𝜎 𝑤 ∙ 𝑥 + 𝑏 directly find w and b Find 𝜇1 , 𝜇2 , Σ −1 𝑤 𝑇 = 𝜇1 − 𝜇2 𝑇 Σ −1 1 1 𝑇 𝑏=− 𝜇 Σ1 −1 𝜇1 2 Will we obtain the same 1 2 𝑁1 𝑇 2 −1 2 set of w and b? + 𝜇 Σ 𝜇 + 𝑙𝑛 2 𝑁2 The same model (function set), but different function may be selected by the same training data. 

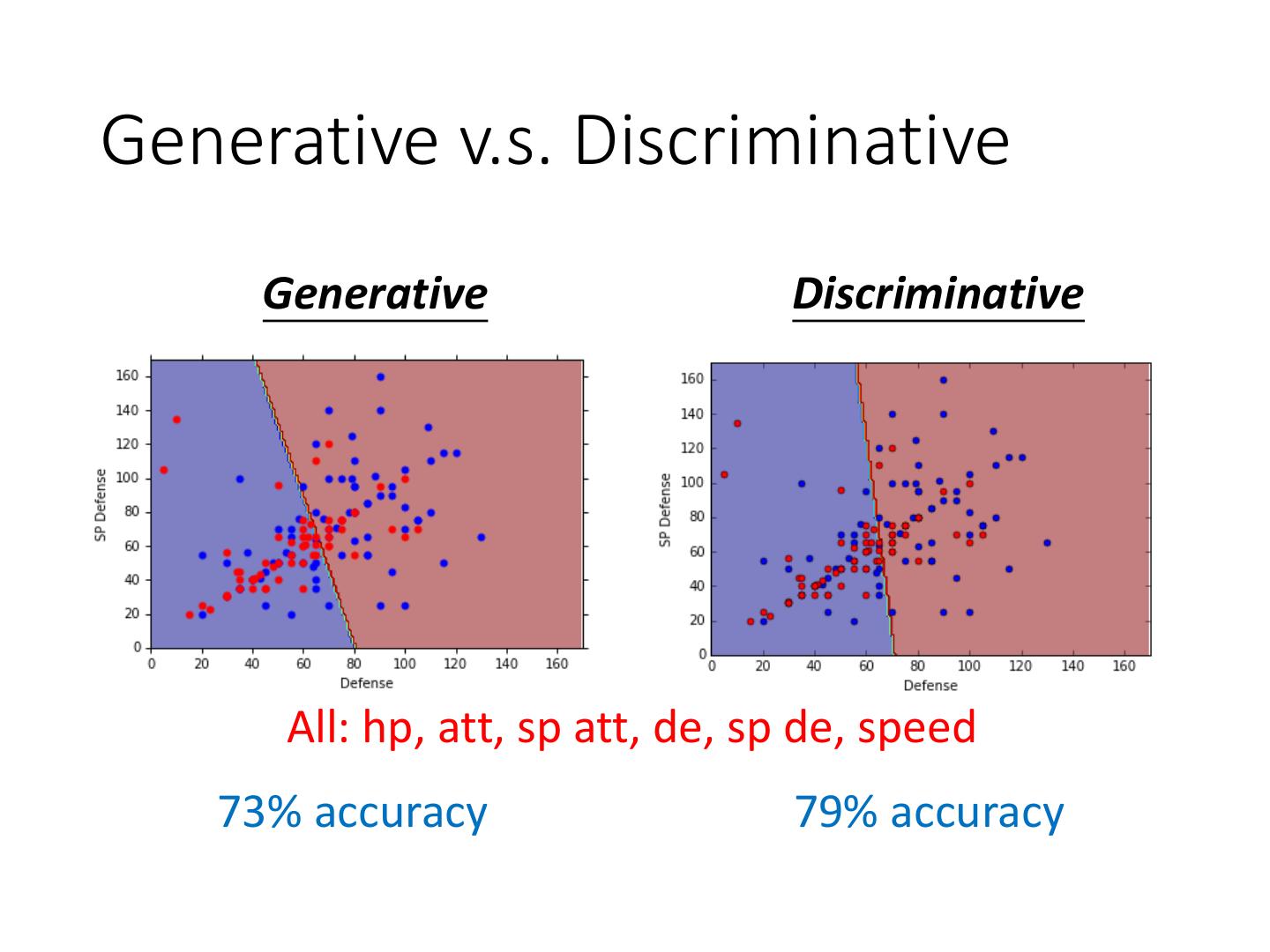
19 .Generative v.s. Discriminative Generative Discriminative All: hp, att, sp att, de, sp de, speed 73% accuracy 79% accuracy 

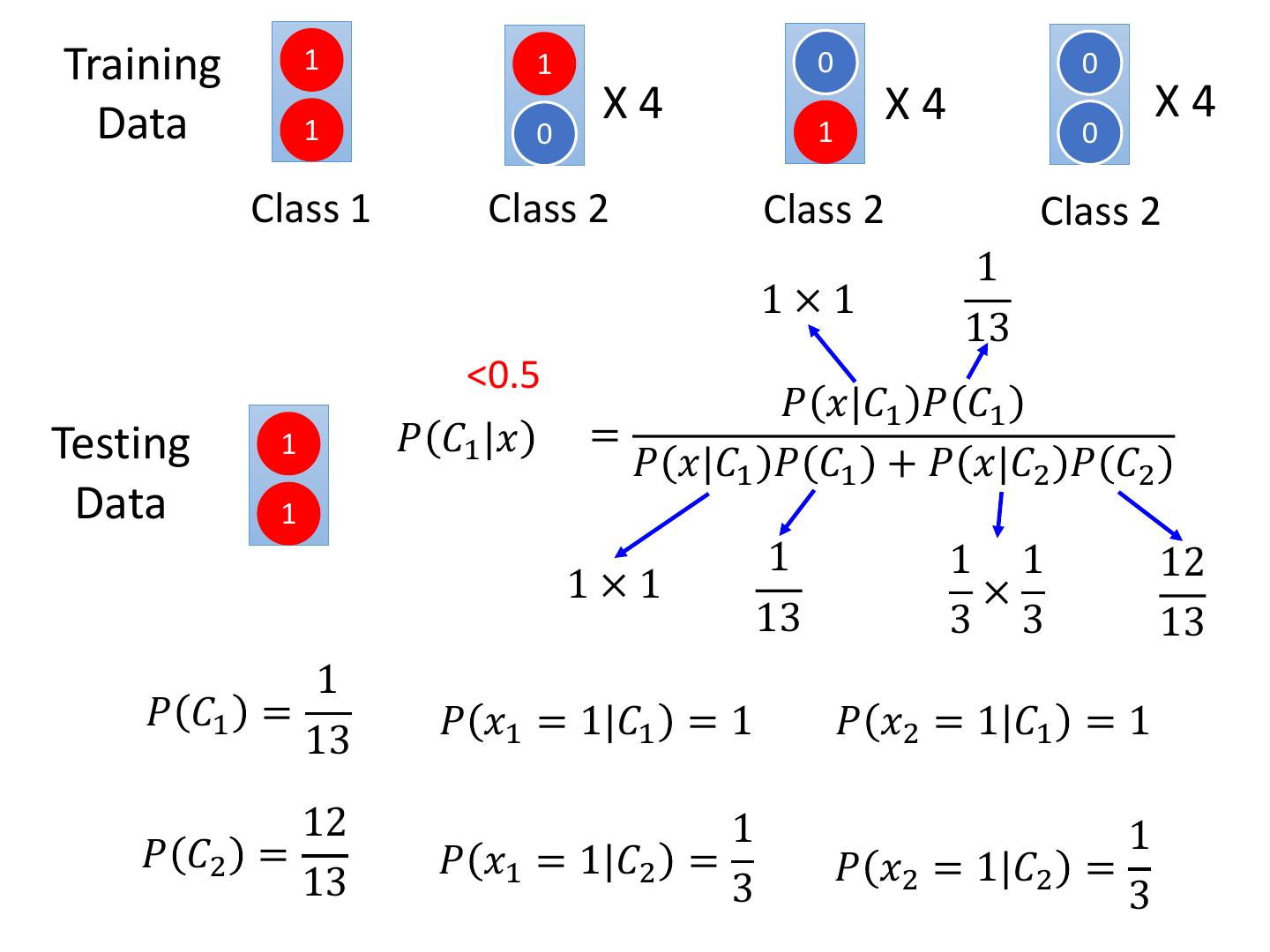
20 . Generative v.s. Discriminative • Example Training 1 1 0 0 Data 1 X4 X4 X4 0 1 0 Class 1 Class 2 Class 2 Class 2 Testing 1 Class 1? How about Naïve Bayes? Data 1 Class 2? 𝑃 𝑥|𝐶𝑖 = 𝑃 𝑥1 |𝐶𝑖 𝑃 𝑥2 |𝐶𝑖 

21 . Generative v.s. Discriminative • Example Training 1 1 0 0 Data 1 X4 X4 X4 0 1 0 Class 1 Class 2 Class 2 Class 2 1 𝑃 𝐶1 = 𝑃 𝑥1 = 1|𝐶1 = 1 𝑃 𝑥2 = 1|𝐶1 = 1 13 12 1 1 𝑃 𝐶2 = 𝑃 𝑥1 = 1|𝐶2 = 𝑃 𝑥2 = 1|𝐶2 = 13 3 3 

22 .Training 1 1 0 0 Data 1 X4 X4 X4 0 1 0 Class 1 Class 2 Class 2 Class 2 1 1×1 13 <0.5 𝑃 𝑥|𝐶1 𝑃 𝐶1 Testing 1 𝑃 𝐶1 |𝑥 = 𝑃 𝑥|𝐶1 𝑃 𝐶1 + 𝑃 𝑥|𝐶2 𝑃 𝐶2 Data 1 1 1 1 12 1×1 × 13 3 3 13 1 𝑃 𝐶1 = 𝑃 𝑥1 = 1|𝐶1 = 1 𝑃 𝑥2 = 1|𝐶1 = 1 13 12 1 1 𝑃 𝐶2 = 𝑃 𝑥1 = 1|𝐶2 = 𝑃 𝑥2 = 1|𝐶2 = 13 3 3 

23 .Generative v.s. Discriminative • Usually people believe discriminative model is better • Benefit of generative model • With the assumption of probability distribution • less training data is needed • more robust to the noise • Priors and class-dependent probabilities can be estimated from different sources. 

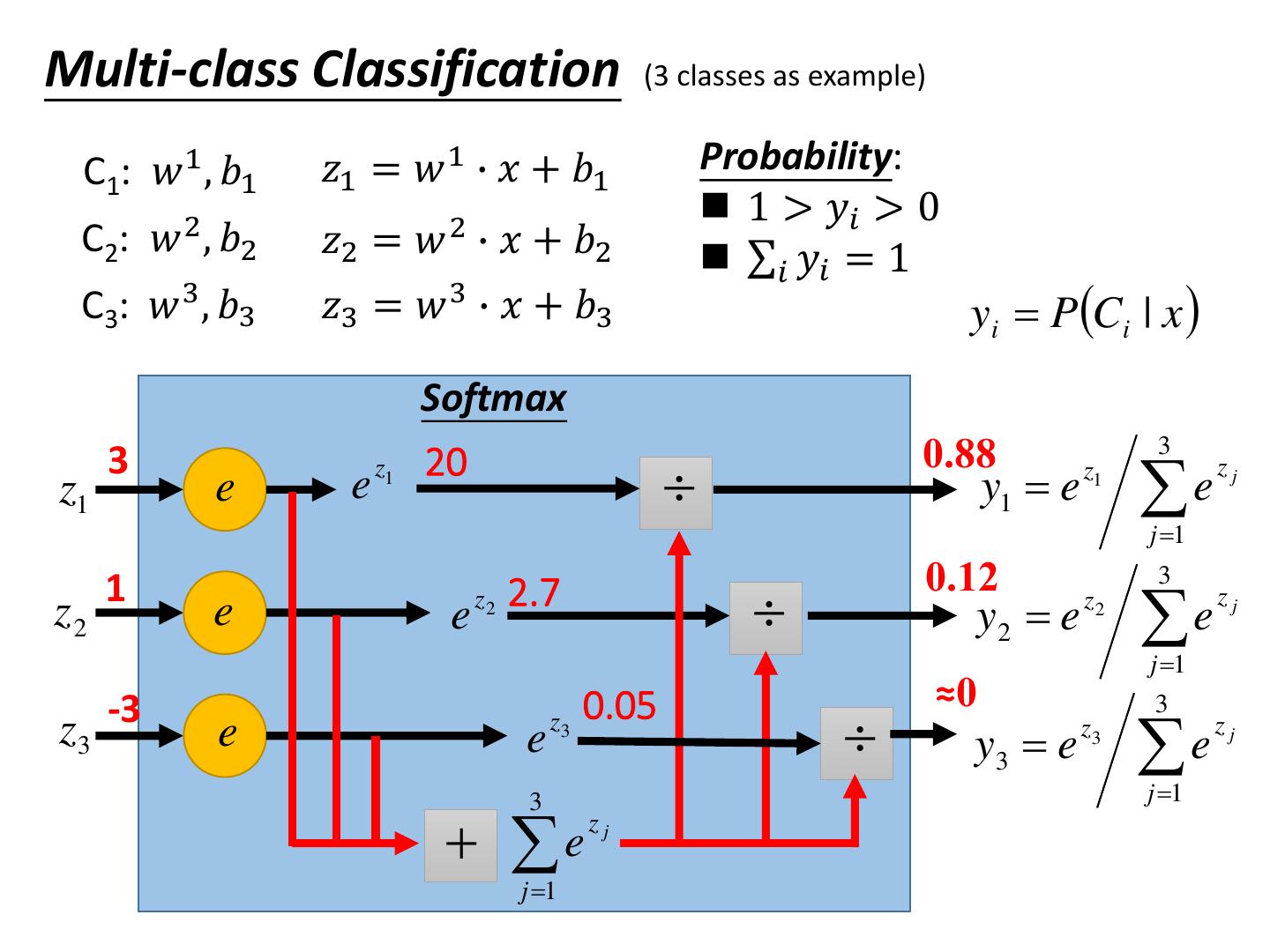
24 .Multi-class Classification (3 classes as example) C1: 𝑤 1 , 𝑏1 𝑧1 = 𝑤 1 ∙ 𝑥 + 𝑏1 Probability:  1 > 𝑦𝑖 > 0 C2: 𝑤 2 , 𝑏2 𝑧2 = 𝑤 2 ∙ 𝑥 + 𝑏2  σ𝑖 𝑦𝑖 = 1 C3: 𝑤 3 , 𝑏3 𝑧3 = 𝑤 3 ∙ 𝑥 + 𝑏3 yi  PCi | x  Softmax 3 0.88 3 e 20 z1 e e z1  y1  e z1 zj j 1 1 0.12 3 z2 e e z 2 2.7  y2  e z2 e zj j 1 0.05 ≈0 z3 -3 3 e e z3  y3  e z3 e zj 3 j 1  e zj j 1 

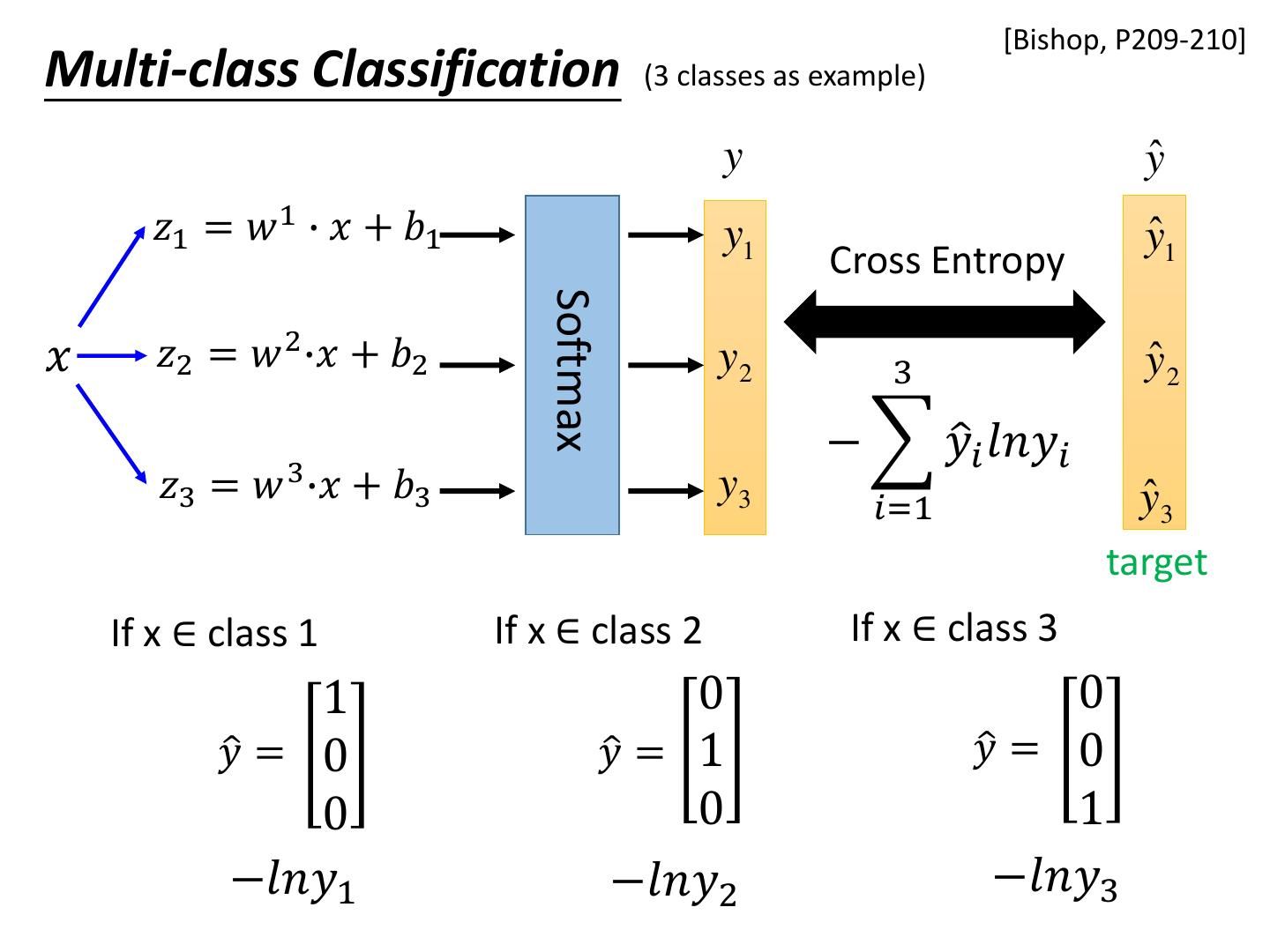
25 . [Bishop, P209-210] Multi-class Classification (3 classes as example) y yˆ 𝑧1 = 𝑤 1 ∙ 𝑥 + 𝑏1 y1 yˆ1 Cross Entropy Softmax 𝑥 𝑧2 = 𝑤 2 ∙𝑥 + 𝑏2 y2 3 yˆ 2 − ෍ 𝑦ො𝑖 𝑙𝑛𝑦𝑖 𝑧3 = 𝑤 3 ∙𝑥 + 𝑏3 y3 yˆ 3 𝑖=1 target If x ∈ class 1 If x ∈ class 2 If x ∈ class 3 1 0 0 𝑦ො = 0 𝑦ො = 1 𝑦ො = 0 0 0 1 −𝑙𝑛𝑦1 −𝑙𝑛𝑦2 −𝑙𝑛𝑦3 

26 . Limitation of Logistic Regression z  w1 x1  w2 x2  b x1 w1 z  Class1 y  0.5 (𝑧 ≥ 0)  y  w2 Class 2 y  0.5 (𝑧 < 0) x2 b Can we? Input Feature x2 Label x1 x2 z≥0 z<0 0 0 Class 2 0 1 Class 1 1 0 Class 1 z<0 z≥0 1 1 Class 2 x1 

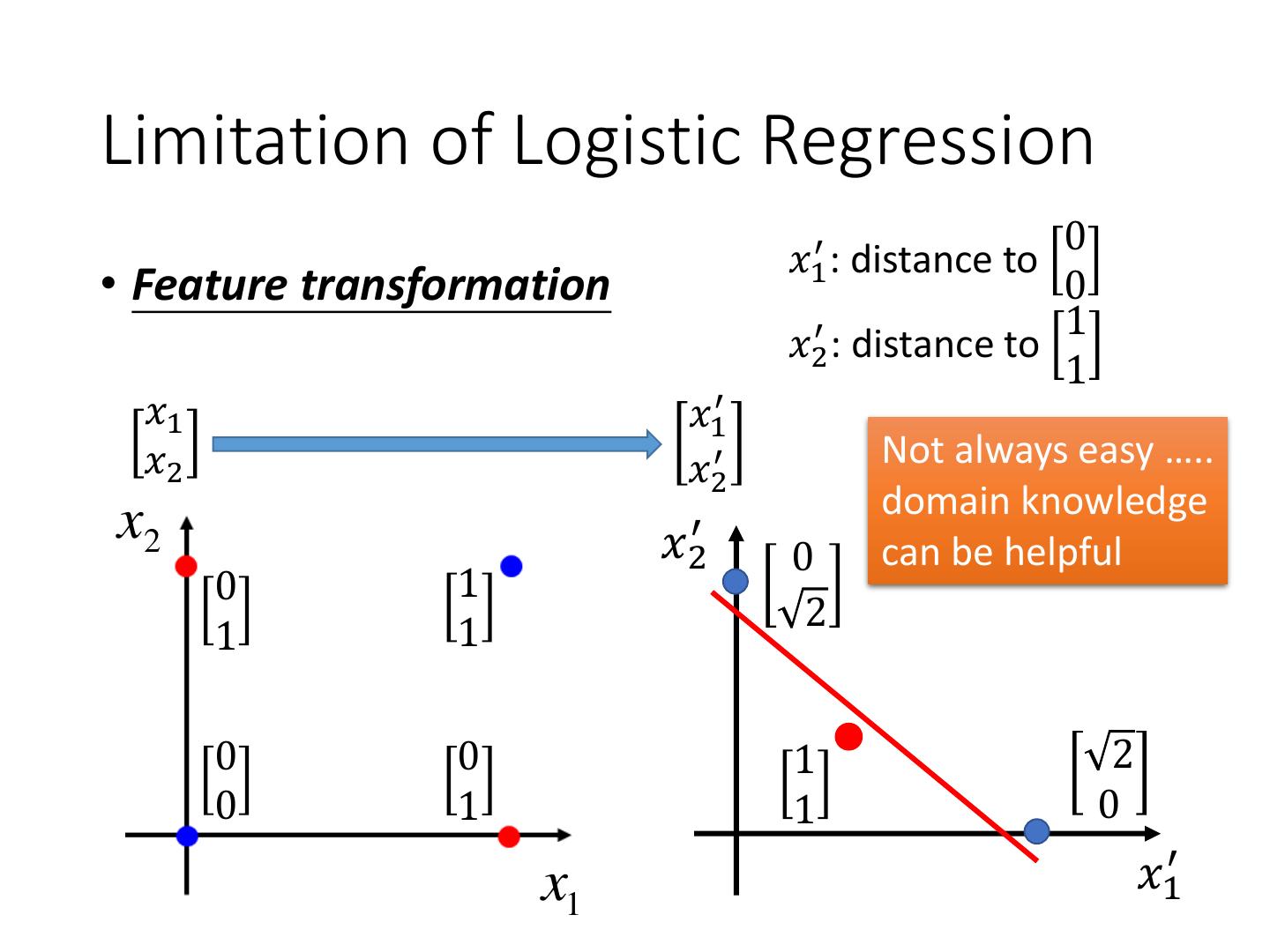
27 .Limitation of Logistic Regression 0 𝑥1′ : distance to • Feature transformation 0 1 𝑥2′ : distance to 1 𝑥1 𝑥1′ 𝑥2 𝑥2′ Not always easy ….. domain knowledge x2 𝑥2′ 0 can be helpful 0 1 1 2 1 0 0 1 2 0 1 1 0 x1 𝑥1′ 

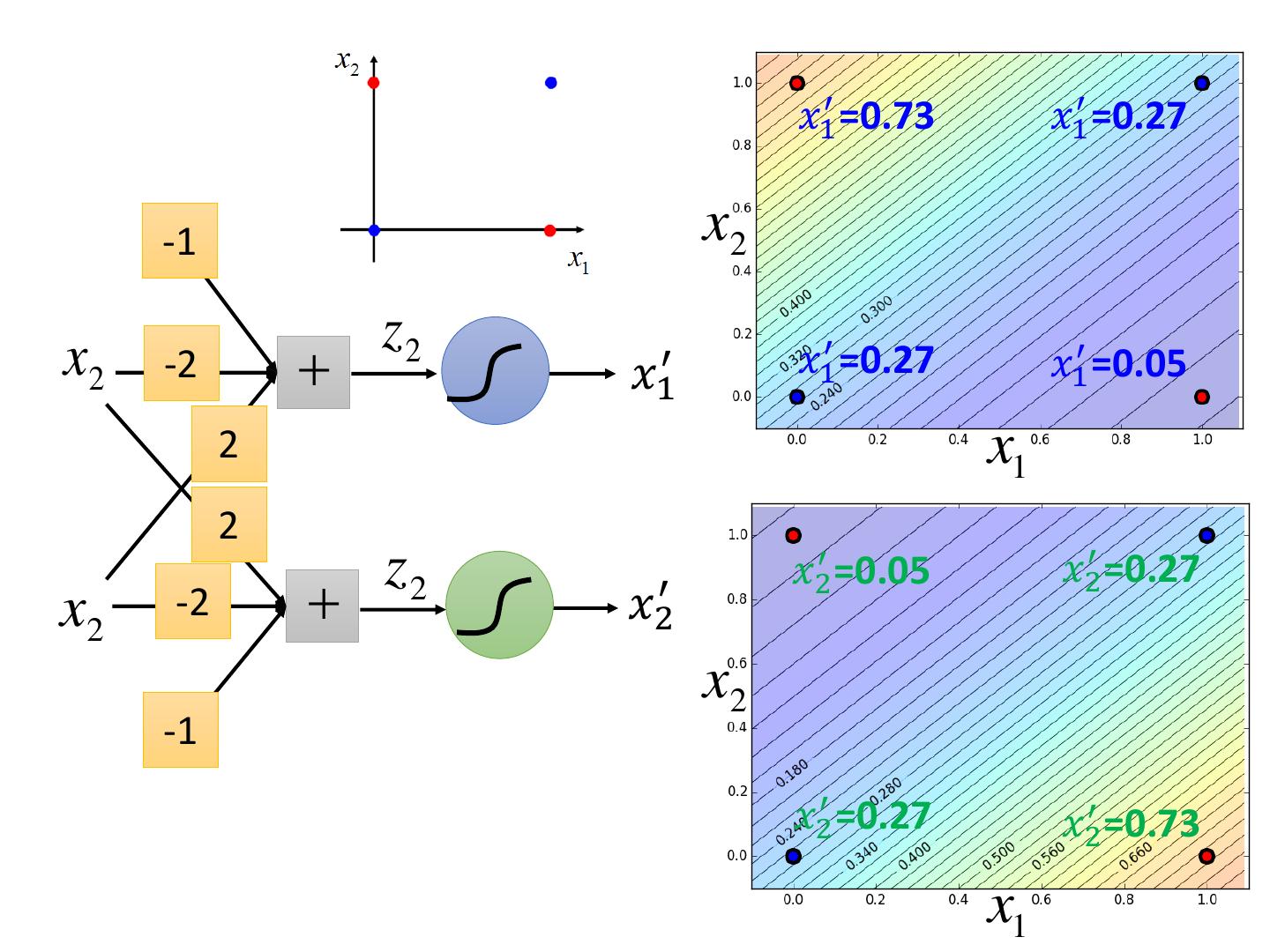
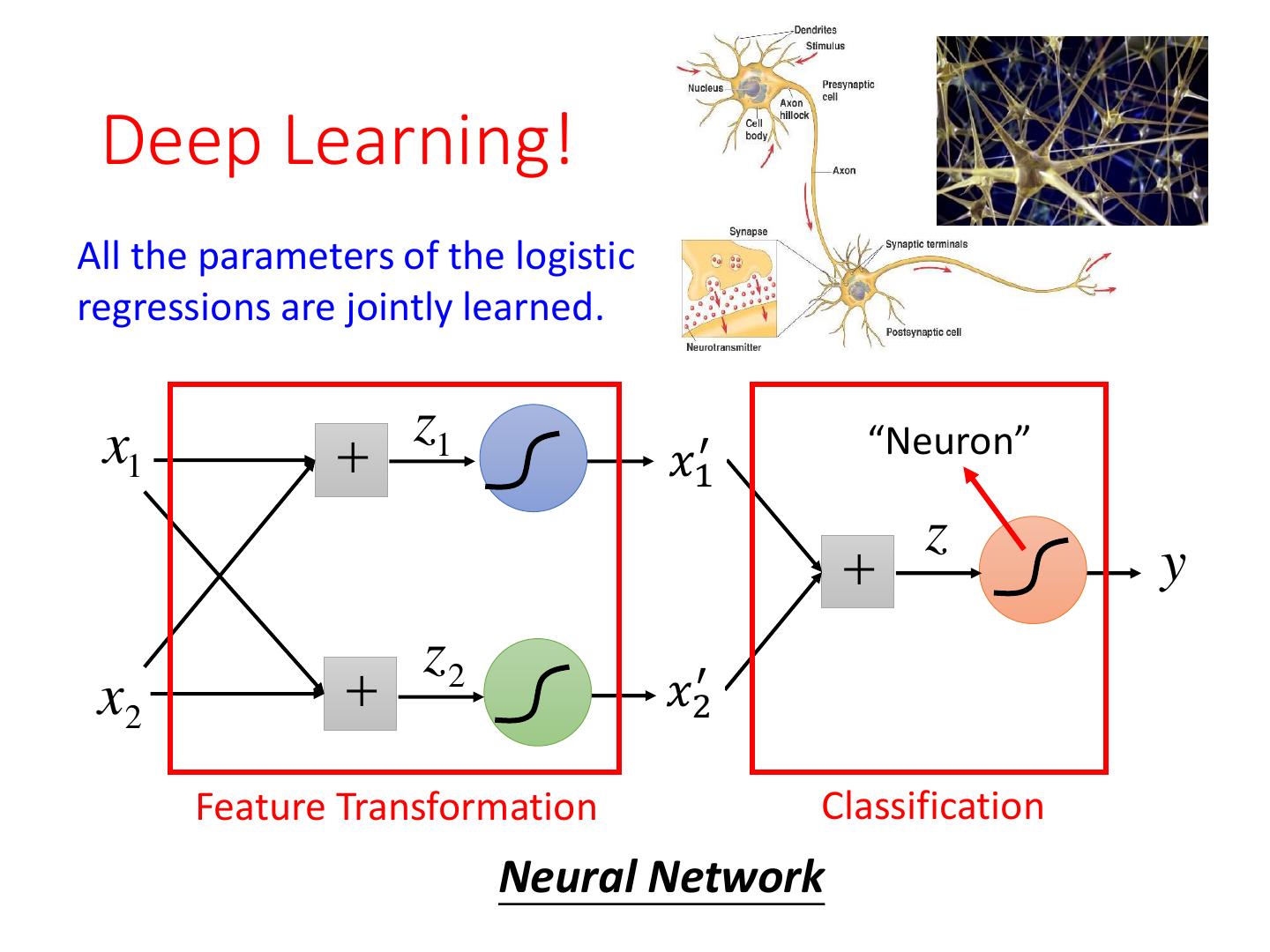
28 .Limitation of Logistic Regression • Cascading logistic regression models z1 x1  𝑥1′ z  y z2 x2  𝑥2′ Feature Transformation Classification (ignore bias in this figure) 

29 . 𝑥1′ =0.73 𝑥1′ =0.27 -1 x2 z2 x2 -2  𝑥1′ 𝑥1′ =0.27 𝑥1′ =0.05 2 x1 2 z2 𝑥2′ =0.05 𝑥2′ =0.27 x2 -2  𝑥2′ x2 -1 𝑥2′ =0.27 𝑥2′ =0.73 x1