Unsupervised Learning: Generation

1 .Unsupervised Learning: Generation 

2 . http://www.rb139.com/index.ph p?s=/Lot/44547 Creation Drawing? Writing Poems? 

3 .Creation • Generative Models: https://openai.com/blog/generative-models/ What I cannot create, I do not understand. Richard Feynman https://www.quora.com/What-did-Richard-Feynman-mean-when-he-said-What-I- cannot-create-I-do-not-understand 

4 .Creation Now v.s. In the future Machine draws a cat http://www.wikihow.com/Draw-a-Cat-Face 

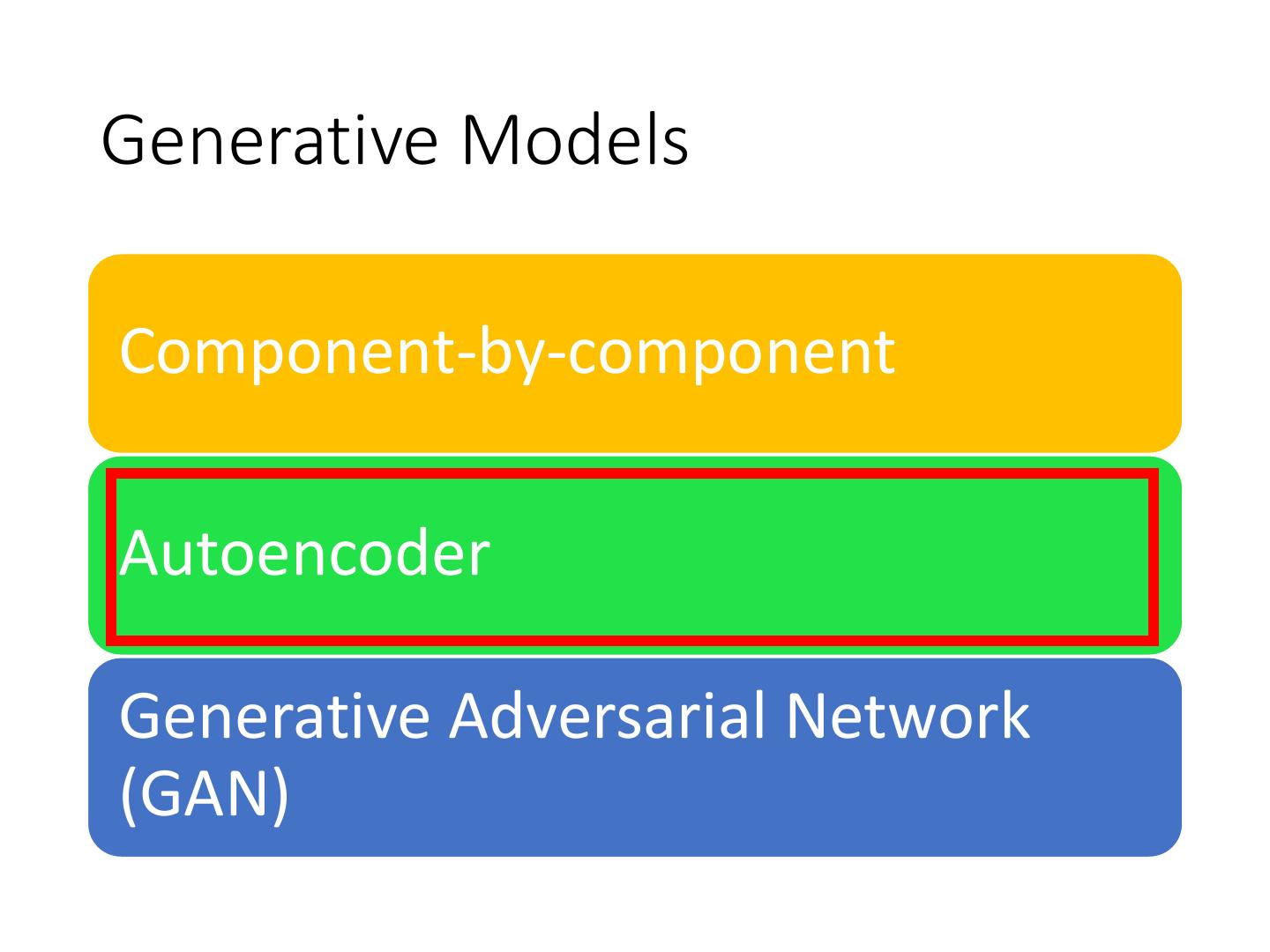
5 .Generative Models Component-by-component Autoencoder Generative Adversarial Network (GAN) 

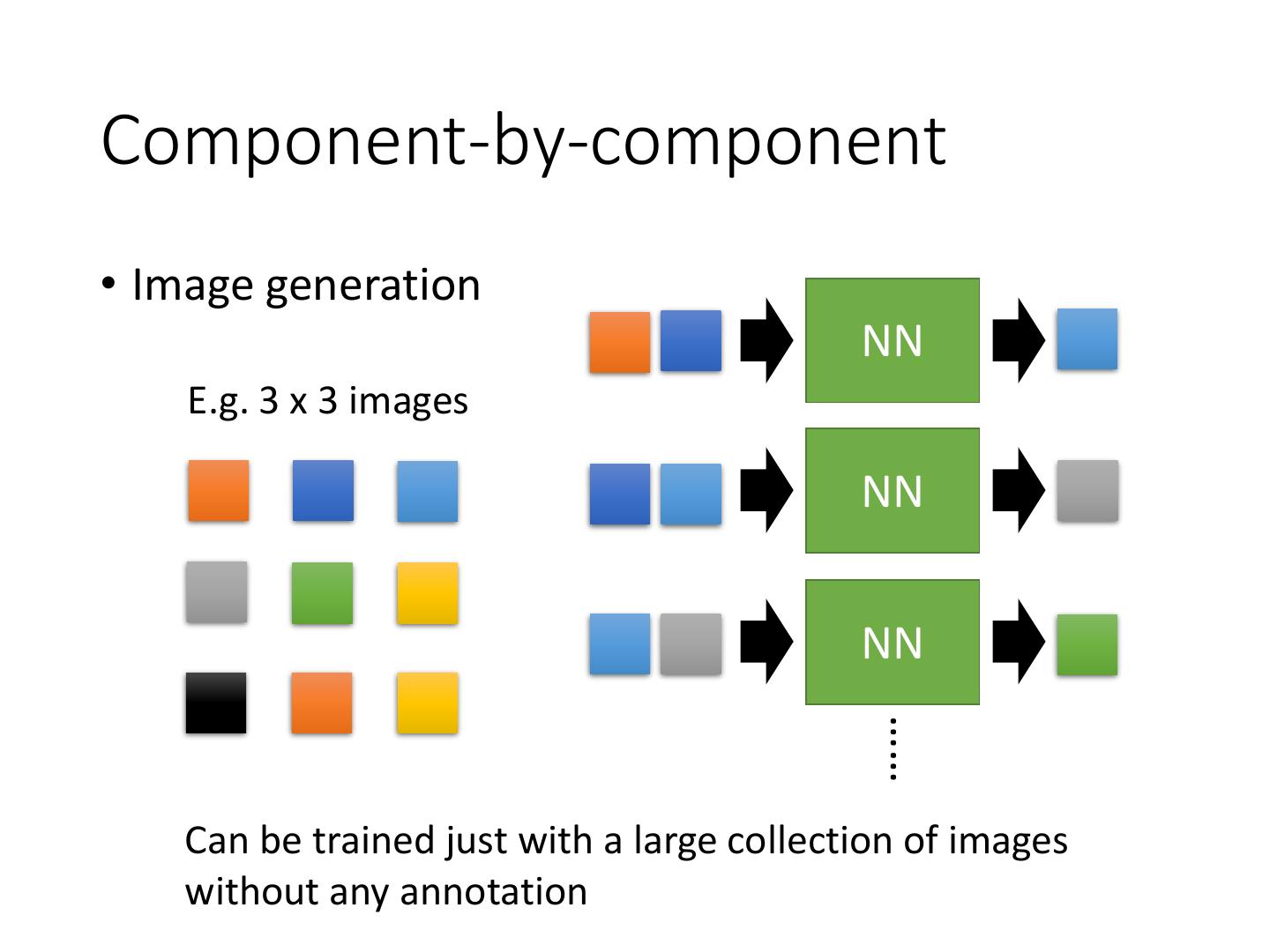
6 .Component-by-component • Image generation NN E.g. 3 x 3 images NN NN …… Can be trained just with a large collection of images without any annotation 

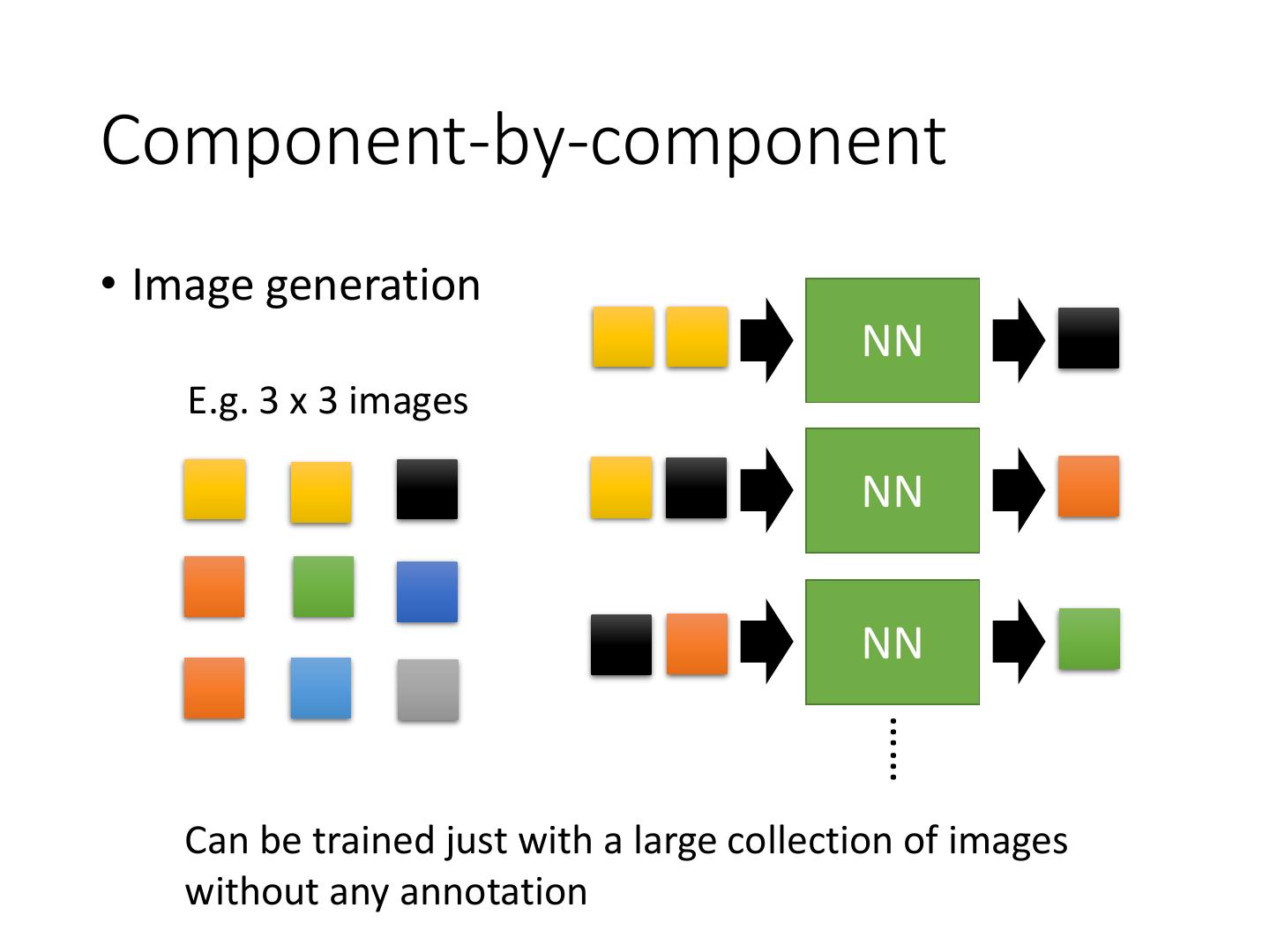
7 .Component-by-component • Image generation NN E.g. 3 x 3 images NN NN …… Can be trained just with a large collection of images without any annotation 

8 .Practicing Generation Models: Pokémon Creation • Small images of 792 Pokémon's • Can machine learn to create new Pokémons? Don't catch them! Create them! • Source of image: http://bulbapedia.bulbagarden.net/wiki/List_of_Pok%C3%A 9mon_by_base_stats_(Generation_VI) Original image is 40 x 40 Making them into 20 x 20 

9 .Practicing Generation Models: Pokémon Creation • Tips (?) ➢ Each pixel is represented by 3 numbers (corresponding to RGB) R=50, G=150, B=100 ➢ Each pixel is represented by a 1-of-N encoding feature 0 0 1 0 0 …… Clustering the similar color 167 colors in total 

10 .Practicing Generation Models: Pokémon Creation • Original image (40 x 40): http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Pokemon_creation/ima ge.rar • Pixels (20 x 20): http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Pokemon_creation/pixe l_color.txt • Each line corresponds to an image, and each number corresponds to a pixel • http://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2016/Pokemon_cre ation/colormap.txt 0 1 2 …… • Following experiment: 1-layer LSTM, 512 cells … 

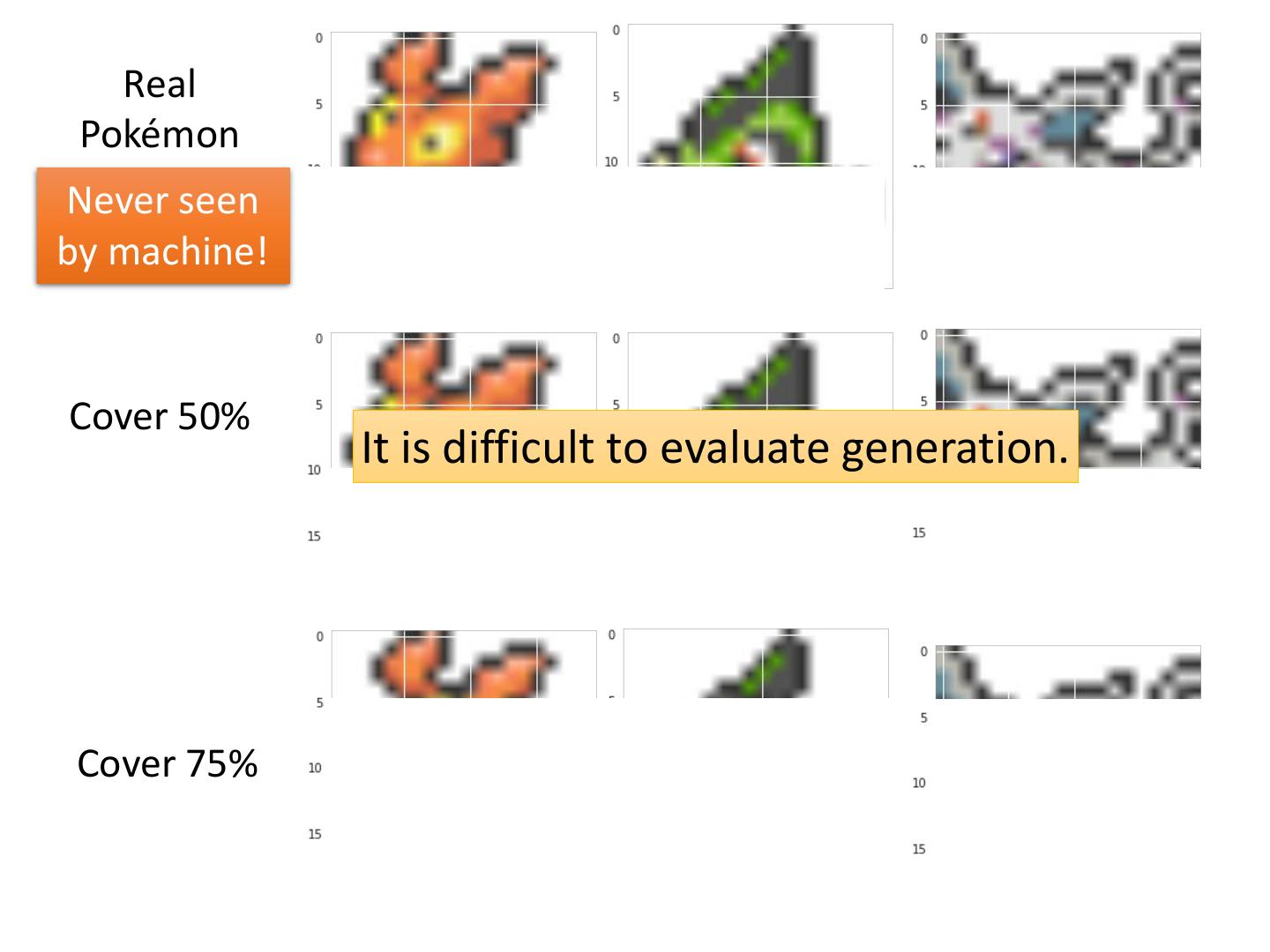
11 . Real Pokémon Never seen by machine! Cover 50% It is difficult to evaluate generation. Cover 75% 

12 . Drawing from scratch Pokémon Creation Need some randomness 

13 . Ref: Aaron van den Oord, Nal Kalchbrenner, Koray PixelRNN Kavukcuoglu, Pixel Recurrent Neural Networks, arXiv preprint, 2016 Real World 

14 .More than images …… Audio: Aaron van den Oord, Sander Dieleman, Heiga Zen, Karen Simonyan, Oriol Vinyals, Alex Graves, Nal Kalchbrenner, Andrew Senior, Koray Kavukcuoglu, WaveNet: A Generative Model for Raw Audio, arXiv preprint, 2016 Video: Nal Kalchbrenner, Aaron van den Oord, Karen Simonyan, Ivo Danihelka, Oriol Vinyals, Alex Graves, Koray Kavukcuoglu, Video Pixel Networks , arXiv preprint, 2016 

15 .Generative Models Component-by-component Autoencoder Generative Adversarial Network (GAN) 

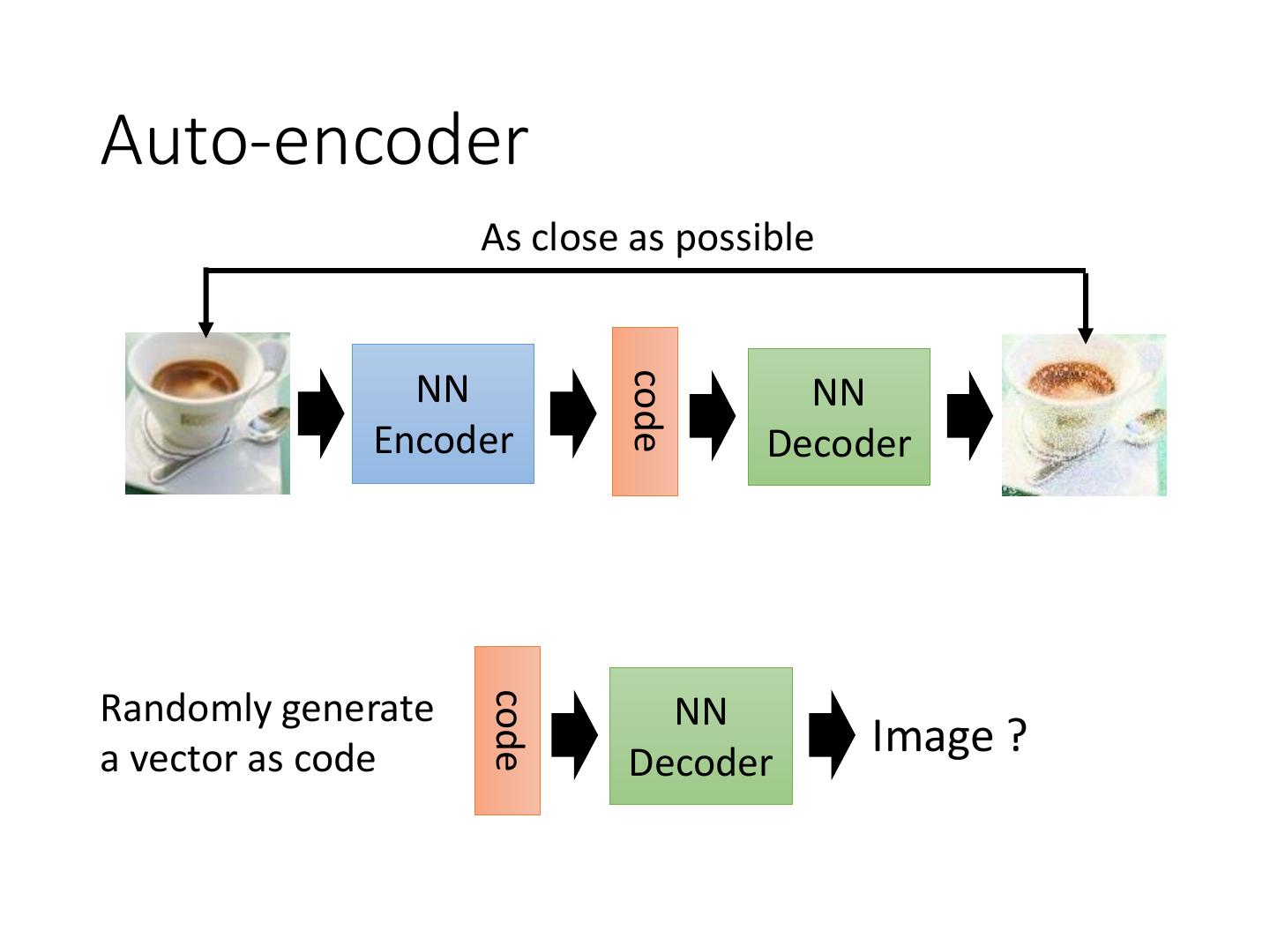
16 .Auto-encoder As close as possible code NN NN Encoder Decoder Randomly generate code NN a vector as code Decoder Image ? 

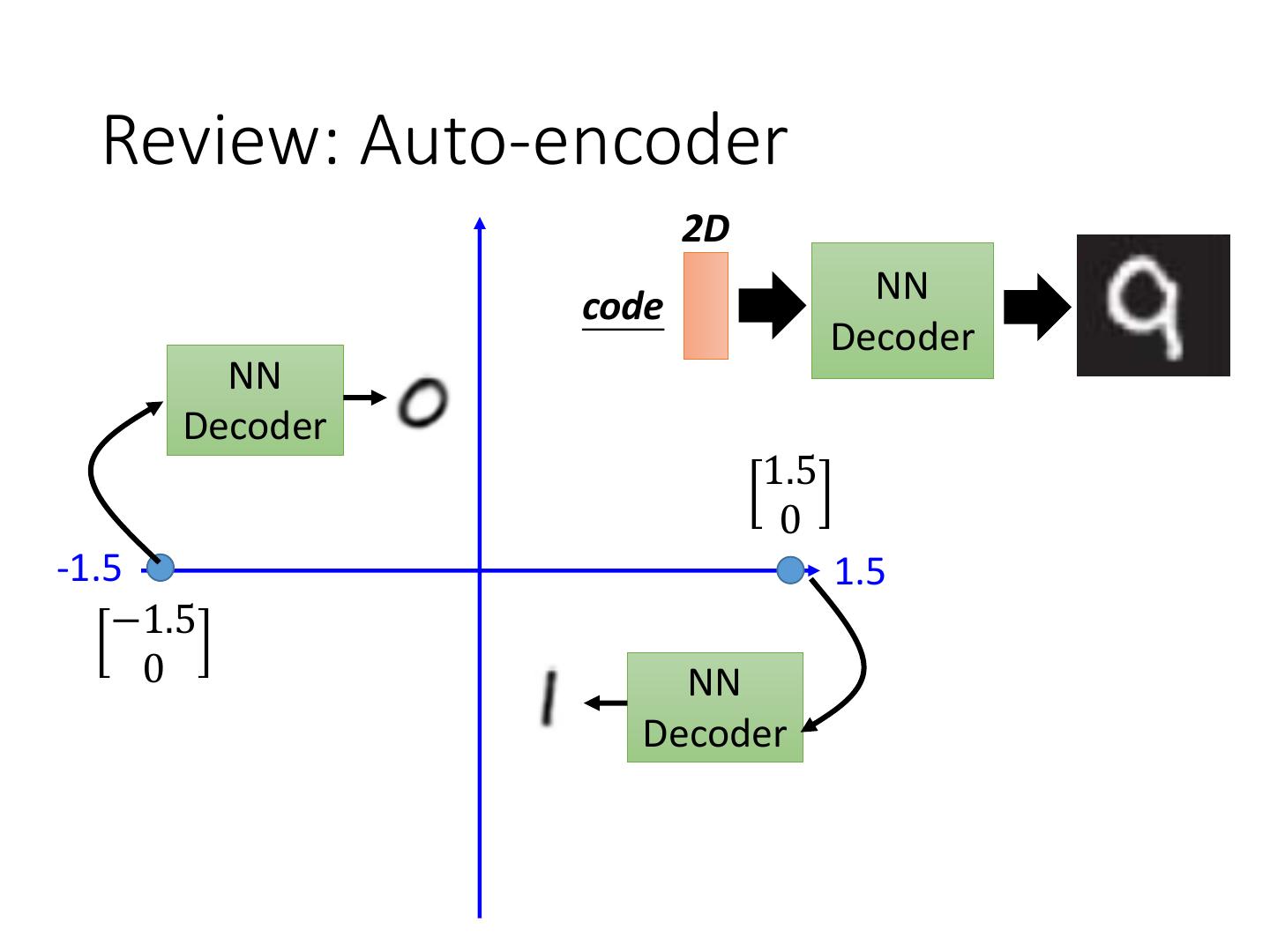
17 . Review: Auto-encoder 2D code NN Decoder NN Decoder 1.5 0 -1.5 1.5 −1.5 0 NN Decoder 

18 .Review: Auto-encoder -1.5 1.5 

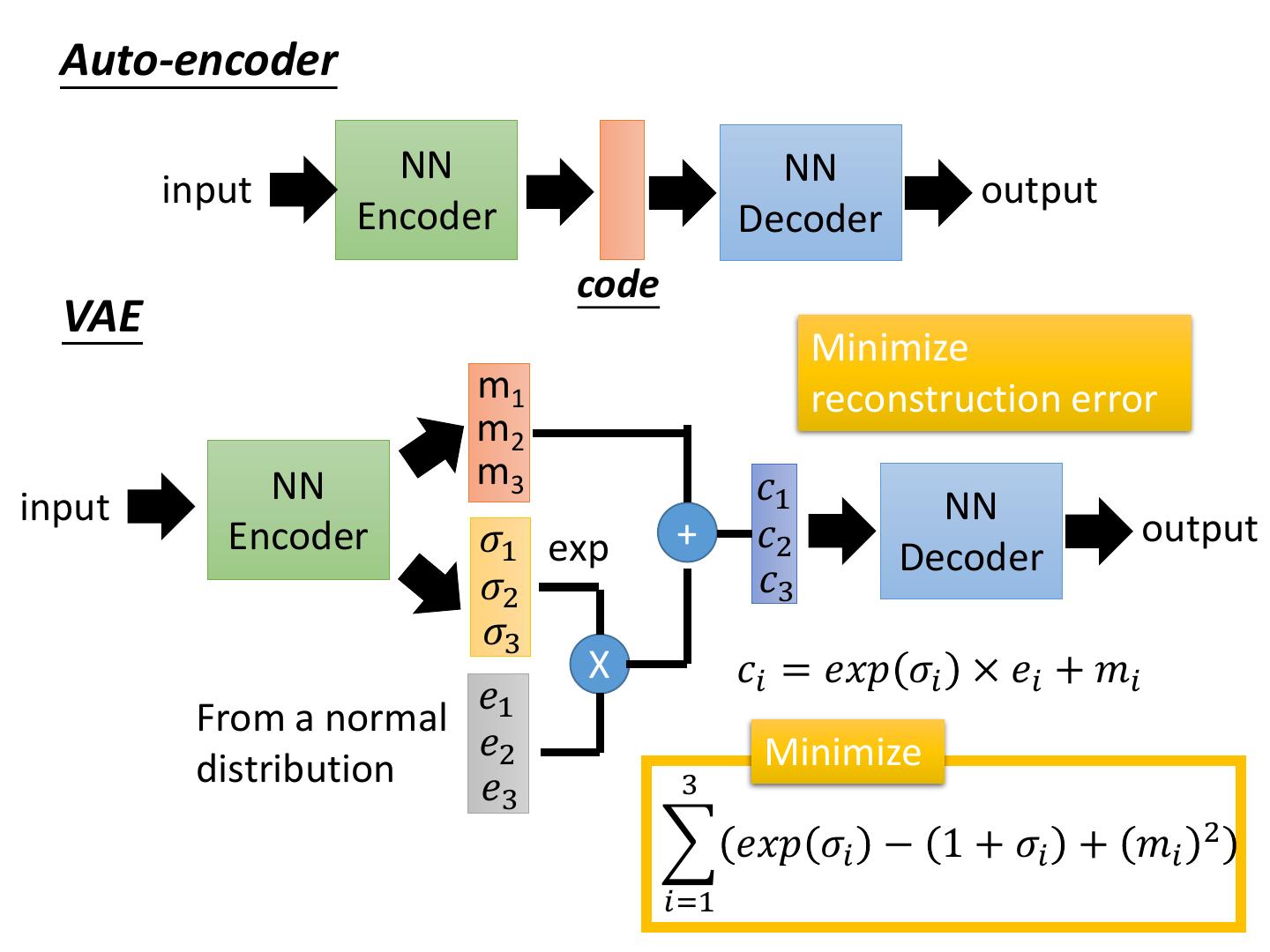
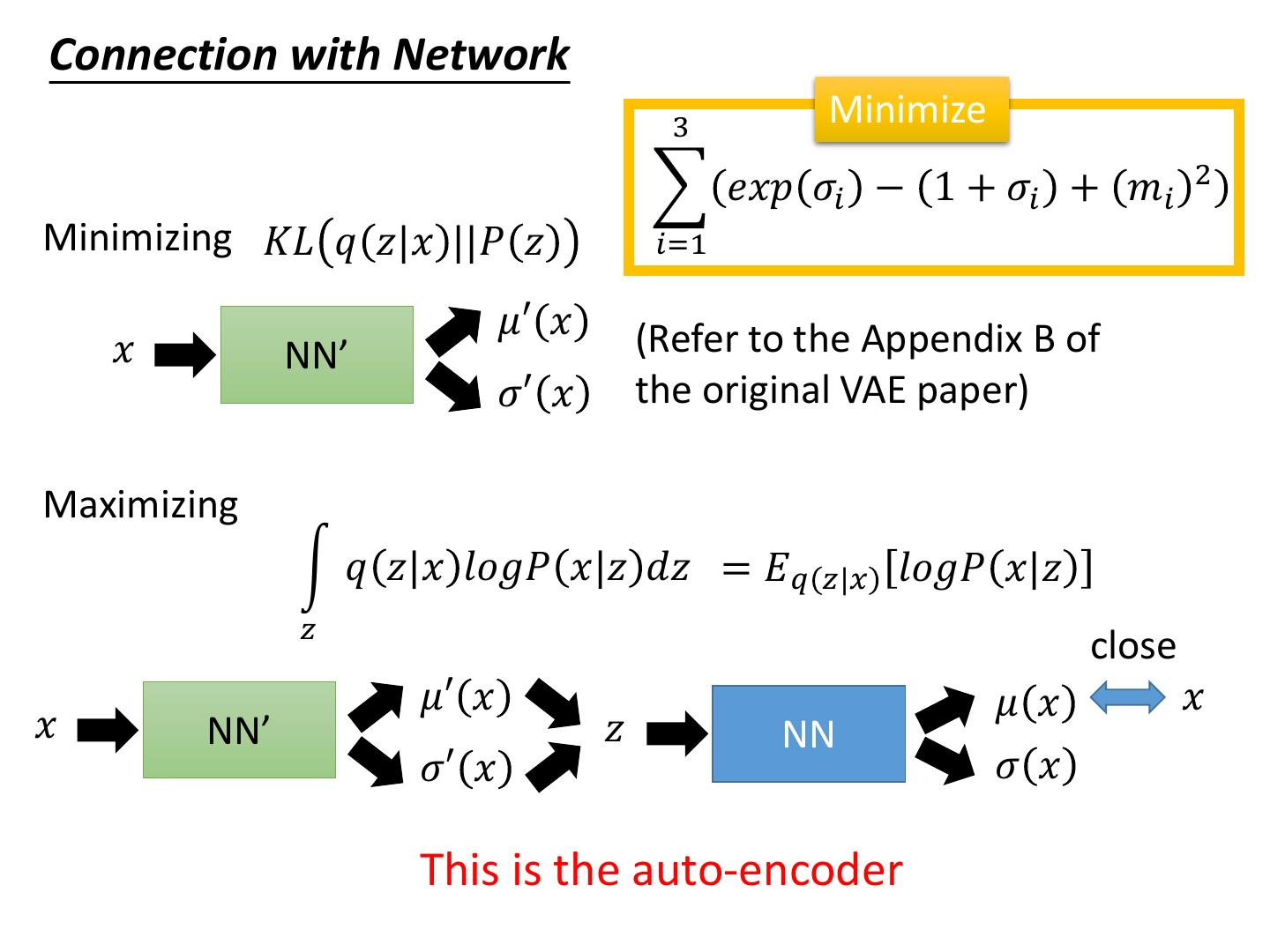
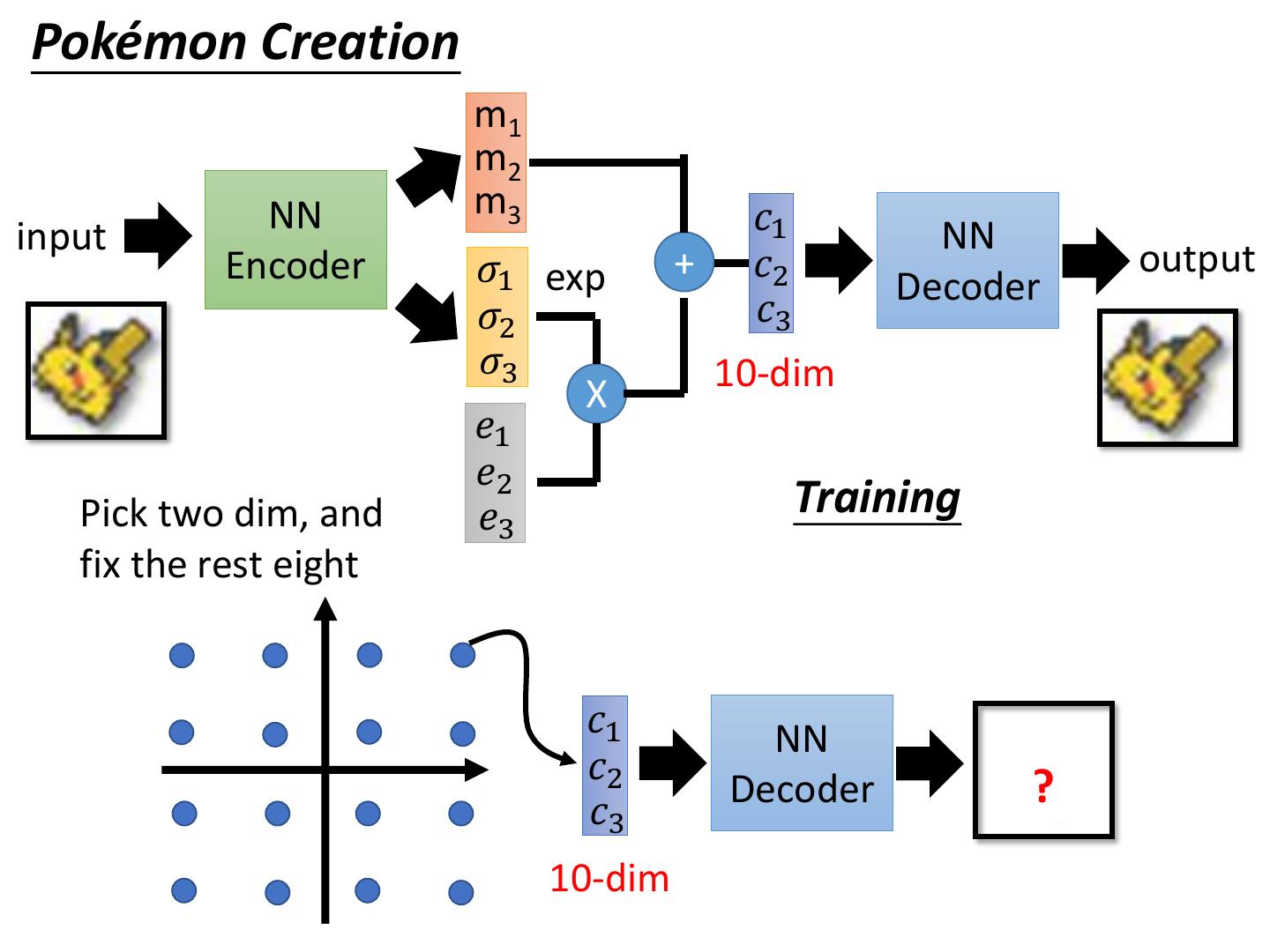
19 . Auto-encoder NN NN input output Encoder Decoder code VAE Minimize m1 reconstruction error m2 NN m3 𝑐1 input NN Encoder 𝜎1 exp + 𝑐2 output Decoder 𝜎2 𝑐3 𝜎3 X 𝑐𝑖 = 𝑒𝑥𝑝 𝜎𝑖 × 𝑒𝑖 + 𝑚𝑖 𝑒 From a normal 1 𝑒2 Minimize distribution 𝑒3 3 ෍ 𝑒𝑥𝑝 𝜎𝑖 − 1 + 𝜎𝑖 + 𝑚𝑖 2 𝑖=1 

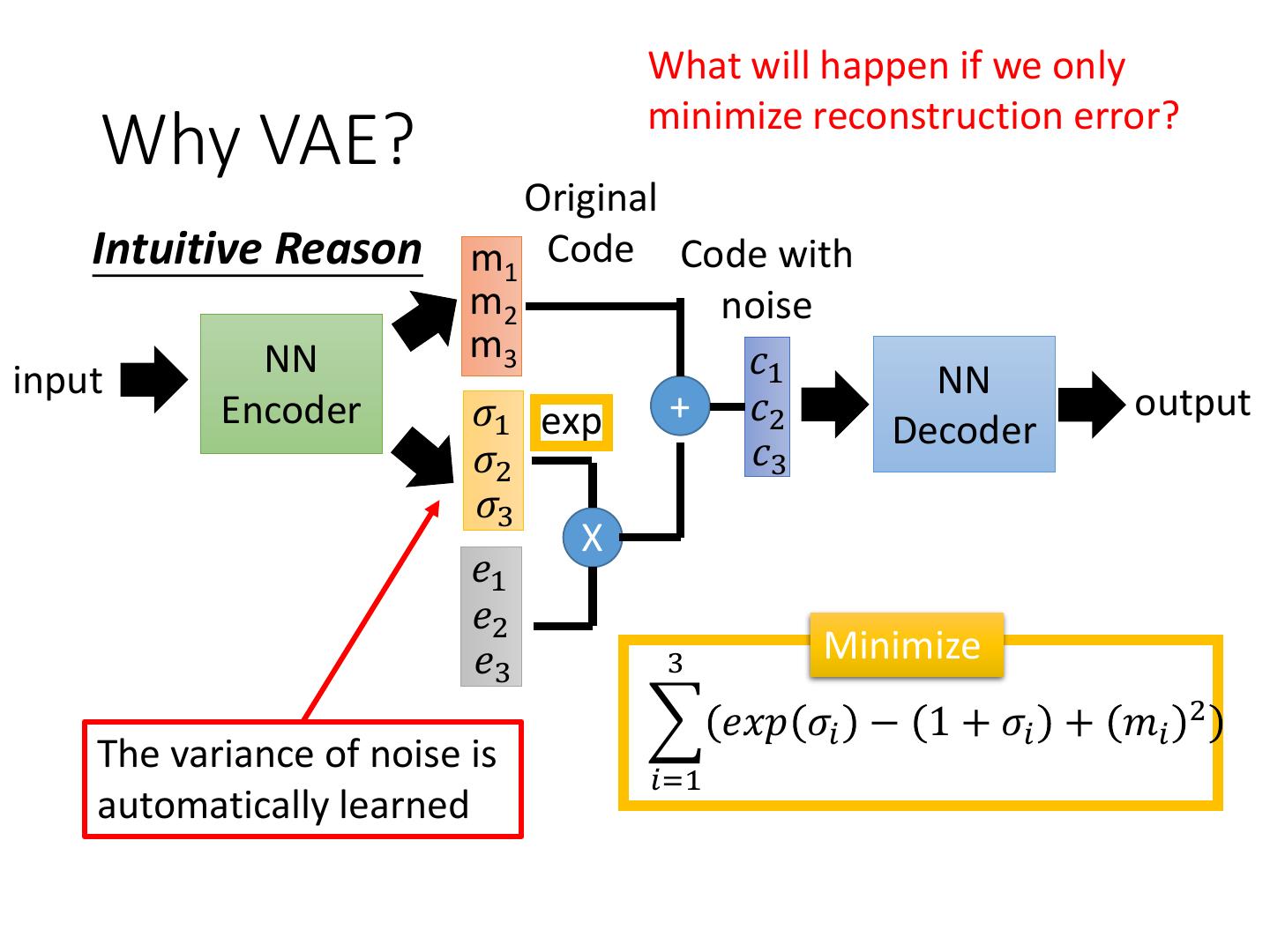
20 . What will happen if we only minimize reconstruction error? Why VAE? Original Intuitive Reason m1 Code Code with m2 noise NN m3 𝑐1 input NN Encoder 𝜎1 exp + 𝑐2 output Decoder 𝜎2 𝑐3 𝜎3 X 𝑒1 𝑒2 𝑒3 3 Minimize ෍ 𝑒𝑥𝑝 𝜎𝑖 − 1 + 𝜎𝑖 + 𝑚𝑖 2 The variance of noise is 𝑖=1 automatically learned 

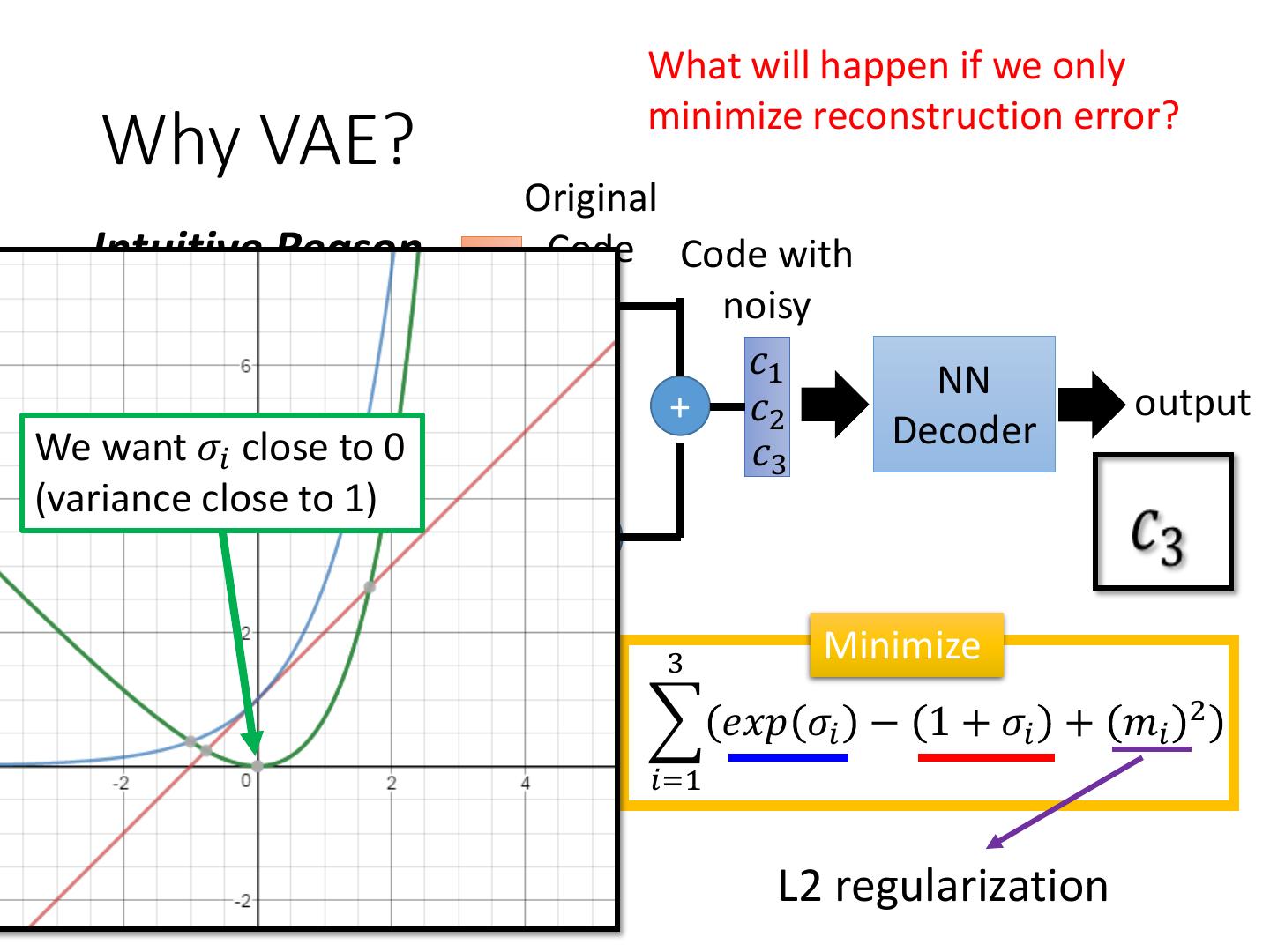
21 . What will happen if we only minimize reconstruction error? Why VAE? Original Intuitive Reason m1 Code Code with m2 noisy NN m3 𝑐1 input NN Encoder 𝜎1 exp + 𝑐2 output We want 𝜎𝑖 close to 0 Decoder 𝜎2 𝑐3 (variance close to 1) 𝜎3 X 𝑒1 𝑒2 𝑒3 3 Minimize ෍ 𝑒𝑥𝑝 𝜎𝑖 − 1 + 𝜎𝑖 + 𝑚𝑖 2 The variance of noise is 𝑖=1 automatically learned L2 regularization 

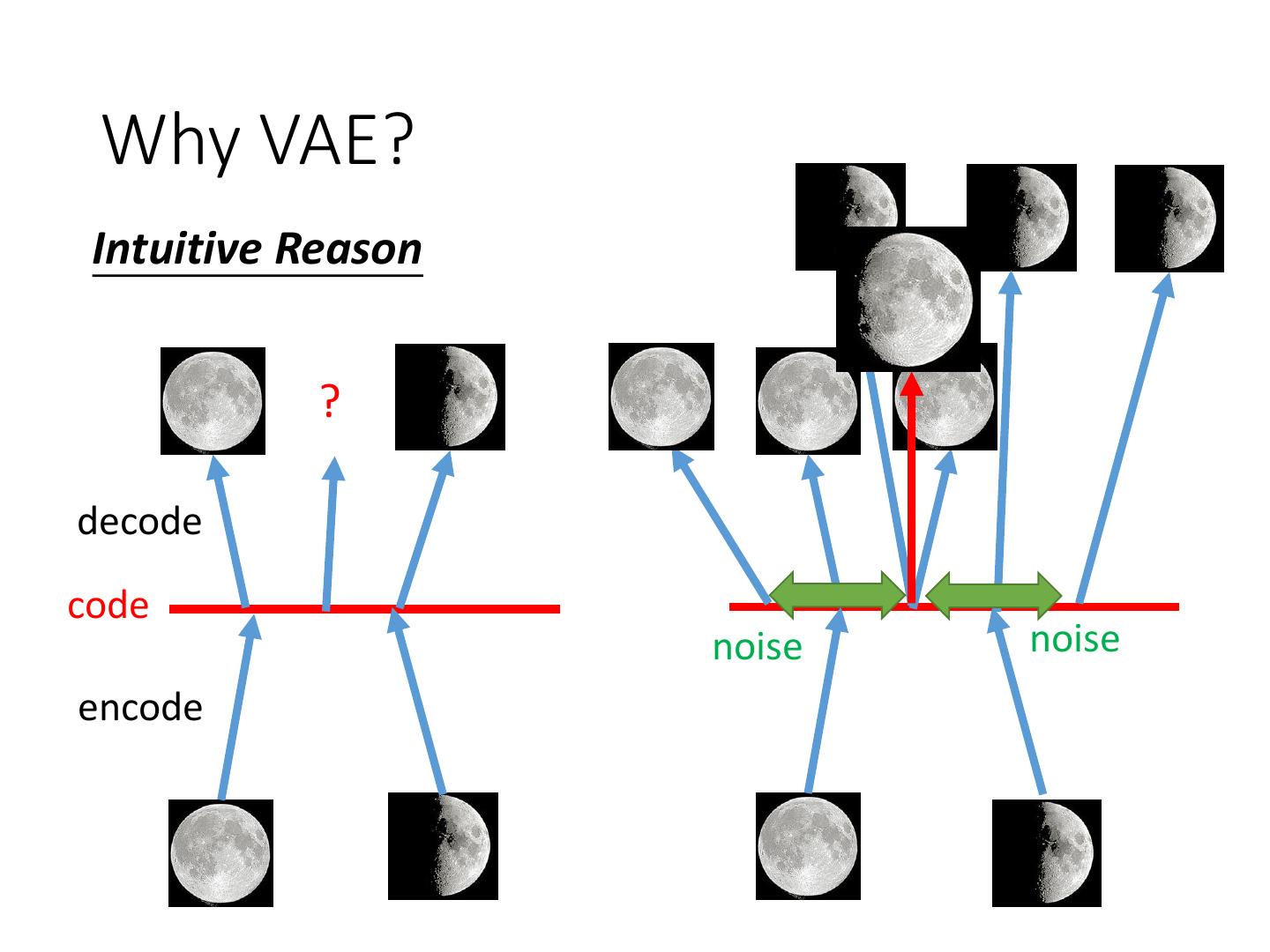
22 . Why VAE? Intuitive Reason ? decode code noise noise encode 

23 .Warning of Math 

24 .Gaussian Mixture Model How to sample? 𝑚~𝑃 𝑚 (multinomial) 𝑃 𝑥 = ෍ 𝑃 𝑚 𝑃 𝑥|𝑚 m is an integer 𝑚 𝑥|𝑚~𝑁 𝜇𝑚 , Σ 𝑚 Each x you generate is from a mixture Distributed representation is better P(x) than cluster. P(m) 1 2 3 4 5 ….. 

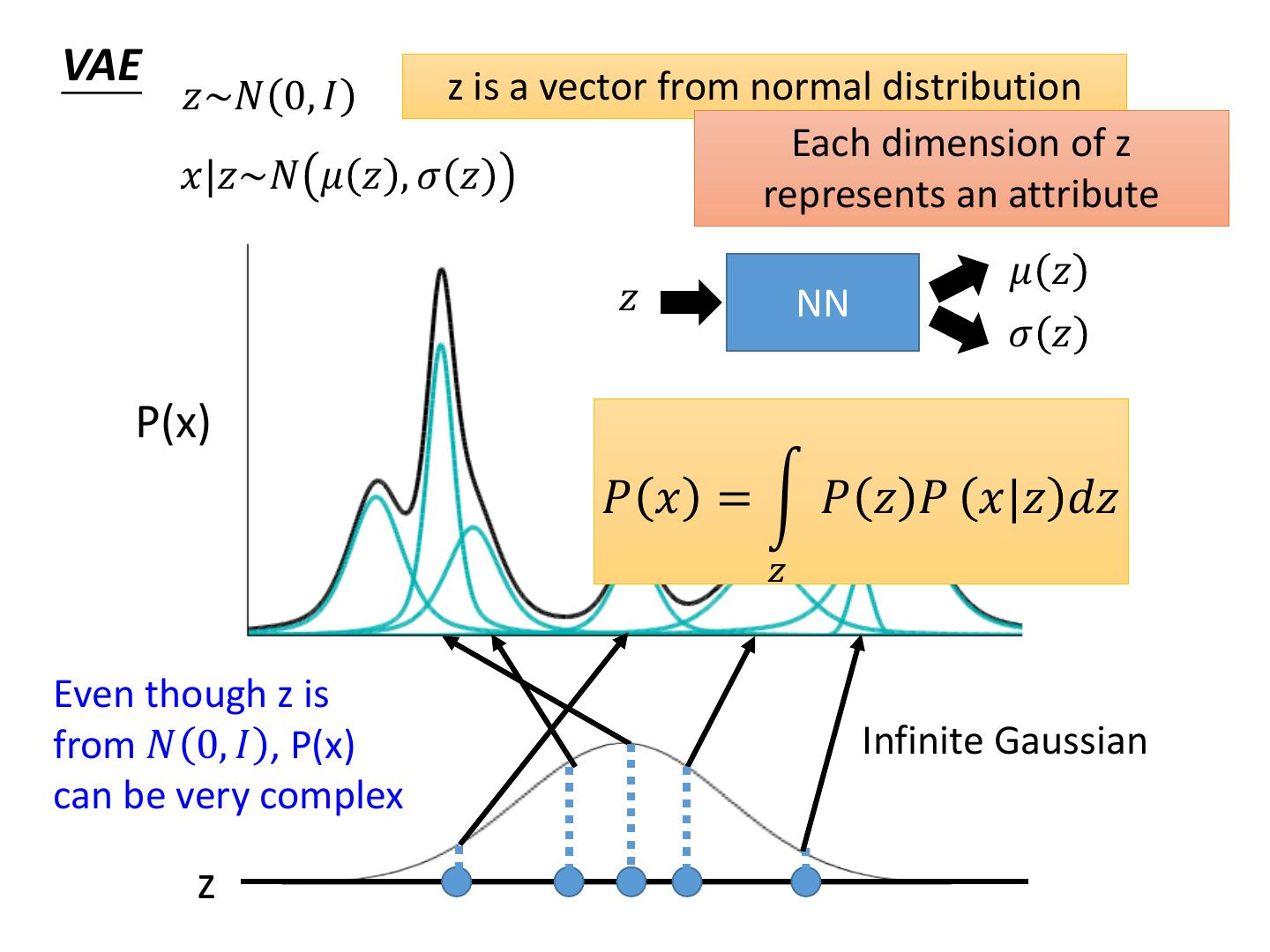
25 .VAE z is a vector from normal distribution 𝑧~𝑁 0, 𝐼 Each dimension of z 𝑥|𝑧~𝑁 𝜇 𝑧 , 𝜎 𝑧 represents an attribute 𝜇 𝑧 𝑧 NN 𝜎 𝑧 P(x) 𝑃 𝑥 = න 𝑃 𝑧 𝑃 𝑥|𝑧 𝑑𝑧 𝑧 Even though z is from 𝑁 0, 𝐼 , P(x) Infinite Gaussian can be very complex z 

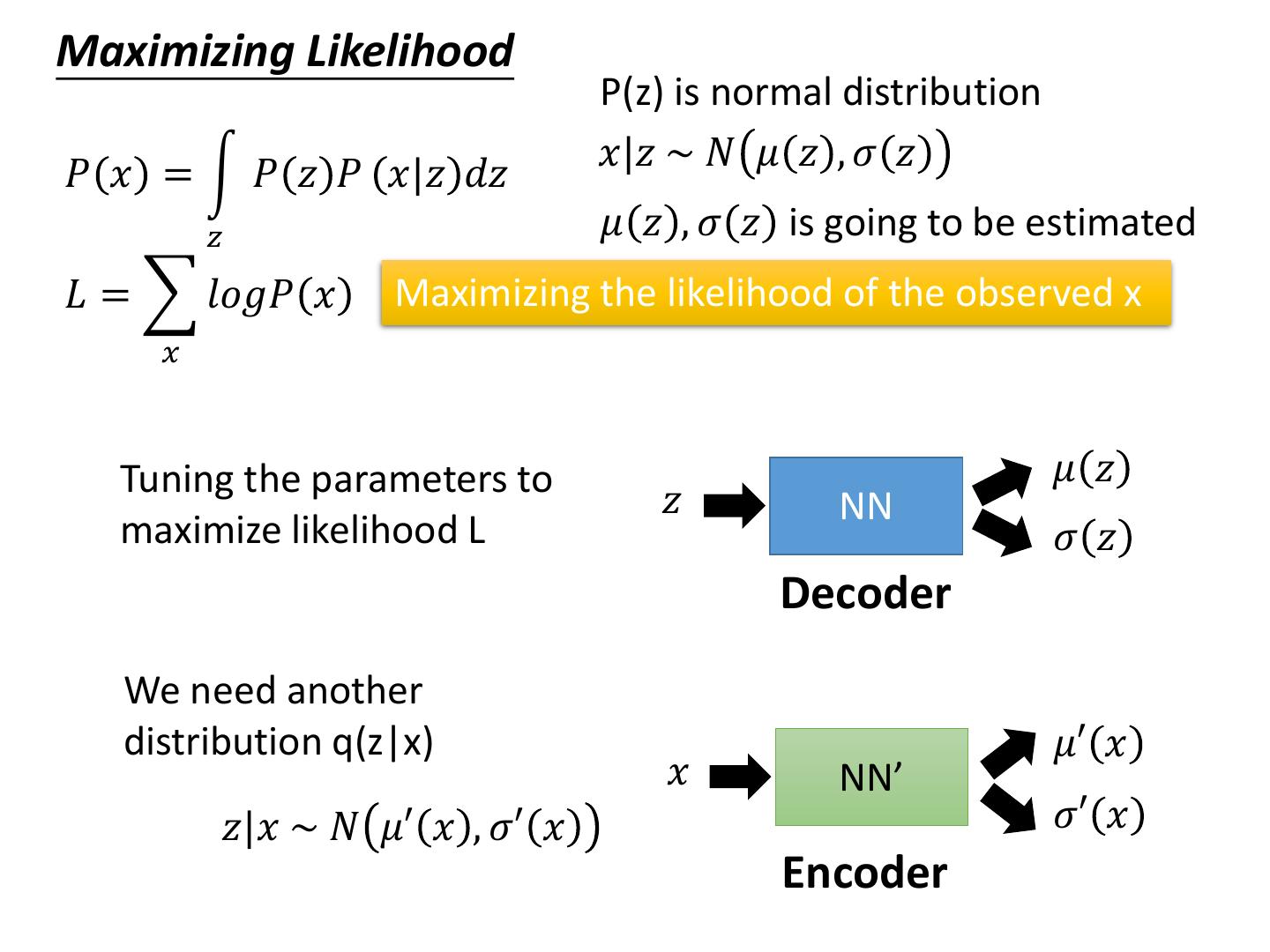
26 .Maximizing Likelihood P(z) is normal distribution 𝑥|𝑧 ~ 𝑁 𝜇 𝑧 , 𝜎 𝑧 𝑃 𝑥 = න 𝑃 𝑧 𝑃 𝑥|𝑧 𝑑𝑧 𝑧 𝜇 𝑧 , 𝜎 𝑧 is going to be estimated 𝐿 = ෍ 𝑙𝑜𝑔𝑃 𝑥 Maximizing the likelihood of the observed x 𝑥 Tuning the parameters to 𝜇 𝑧 𝑧 NN maximize likelihood L 𝜎 𝑧 Decoder We need another distribution q(z|x) 𝜇′ 𝑥 𝑥 NN’ 𝑧|𝑥 ~ 𝑁 𝜇′ 𝑥 , 𝜎′ 𝑥 𝜎′ 𝑥 Encoder 

27 .Maximizing Likelihood P(z) is normal distribution 𝑥|𝑧 ~ 𝑁 𝜇 𝑧 , 𝜎 𝑧 𝑃 𝑥 = න 𝑃 𝑧 𝑃 𝑥|𝑧 𝑑𝑧 𝑧 𝜇 𝑧 , 𝜎 𝑧 is going to be estimated 𝐿 = ෍ 𝑙𝑜𝑔𝑃 𝑥 Maximizing the likelihood of the observed x 𝑥 𝑙𝑜𝑔𝑃 𝑥 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔𝑃 𝑥 𝑑𝑧 q(z|x) can be any distribution 𝑧 𝑃 𝑧, 𝑥 𝑃 𝑧, 𝑥 𝑞 𝑧|𝑥 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 𝑃 𝑧|𝑥 𝑞 𝑧|𝑥 𝑃 𝑧|𝑥 𝑧 𝑧 𝑃 𝑧, 𝑥 𝑞 𝑧|𝑥 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 + න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 𝑞 𝑧|𝑥 𝑃 𝑧|𝑥 𝑧 𝑧 𝐾𝐿 𝑞 𝑧|𝑥 ||𝑃 𝑧|𝑥 ≥0 𝑃 𝑥|𝑧 𝑃 𝑧 ≥ න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 𝑙𝑜𝑤𝑒𝑟 𝑏𝑜𝑢𝑛𝑑 𝐿𝑏 𝑞 𝑧|𝑥 𝑧 

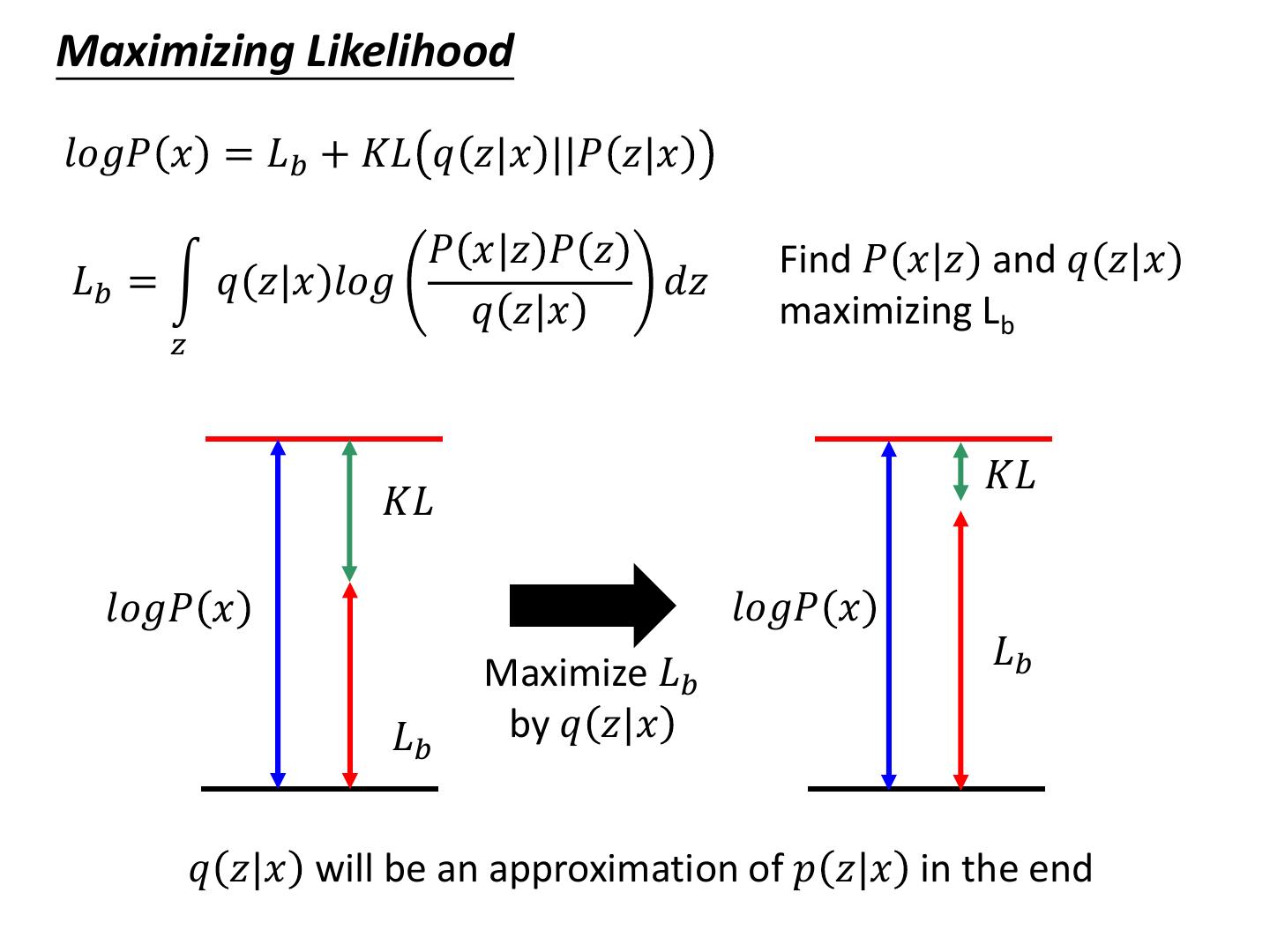
28 .Maximizing Likelihood 𝑙𝑜𝑔𝑃 𝑥 = 𝐿𝑏 + 𝐾𝐿 𝑞 𝑧|𝑥 ||𝑃 𝑧|𝑥 𝑃 𝑥|𝑧 𝑃 𝑧 Find 𝑃 𝑥|𝑧 and 𝑞 𝑧|𝑥 𝐿𝑏 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 𝑞 𝑧|𝑥 maximizing Lb 𝑧 𝐾𝐿 𝐾𝐿 𝑙𝑜𝑔𝑃 𝑥 𝑙𝑜𝑔𝑃 𝑥 𝐿𝑏 Maximize 𝐿𝑏 𝐿𝑏 by 𝑞 𝑧|𝑥 𝑞 𝑧|𝑥 will be an approximation of 𝑝 𝑧|𝑥 in the end 

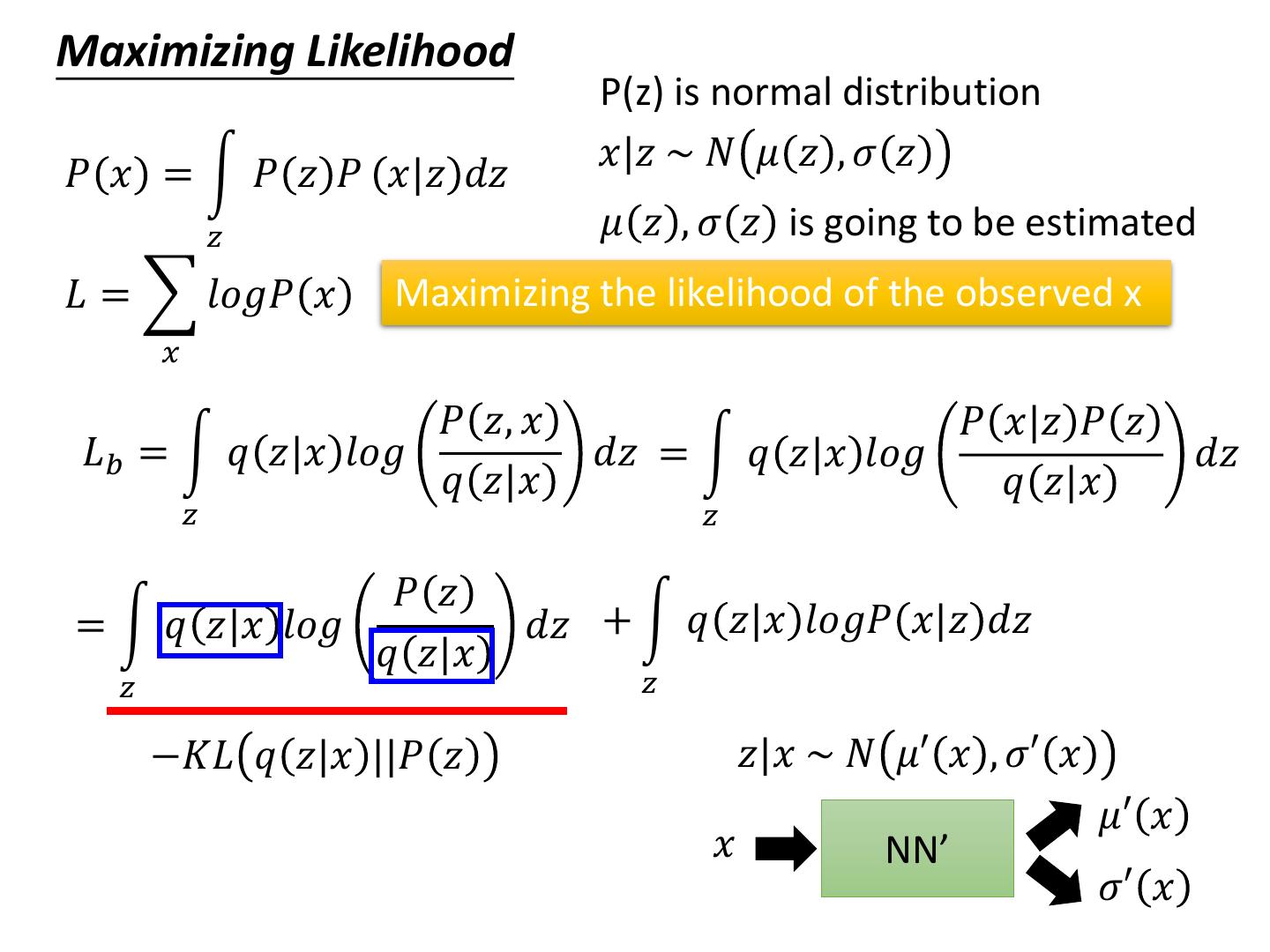
29 .Maximizing Likelihood P(z) is normal distribution 𝑥|𝑧 ~ 𝑁 𝜇 𝑧 , 𝜎 𝑧 𝑃 𝑥 = න 𝑃 𝑧 𝑃 𝑥|𝑧 𝑑𝑧 𝑧 𝜇 𝑧 , 𝜎 𝑧 is going to be estimated 𝐿 = ෍ 𝑙𝑜𝑔𝑃 𝑥 Maximizing the likelihood of the observed x 𝑥 𝑃 𝑧, 𝑥 𝑃 𝑥|𝑧 𝑃 𝑧 𝐿𝑏 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 𝑞 𝑧|𝑥 𝑞 𝑧|𝑥 𝑧 𝑧 𝑃 𝑧 = න 𝑞 𝑧|𝑥 𝑙𝑜𝑔 𝑑𝑧 + න 𝑞 𝑧|𝑥 𝑙𝑜𝑔𝑃 𝑥|𝑧 𝑑𝑧 𝑞 𝑧|𝑥 𝑧 𝑧 −𝐾𝐿 𝑞 𝑧|𝑥 ||𝑃 𝑧 𝑧|𝑥 ~ 𝑁 𝜇′ 𝑥 , 𝜎′ 𝑥 𝜇′ 𝑥 𝑥 NN’ 𝜎′ 𝑥