Ensemble

1 .Ensemble 

2 .Framework of Ensemble • Get a set of classifiers • 𝑓1 𝑥 , 𝑓2 𝑥 , 𝑓3 𝑥 , …… 坦 補 DD They should be diverse. • Aggregate the classifiers (properly) • 在打王時每個人都有該站的位置 

3 .Ensemble: Bagging 

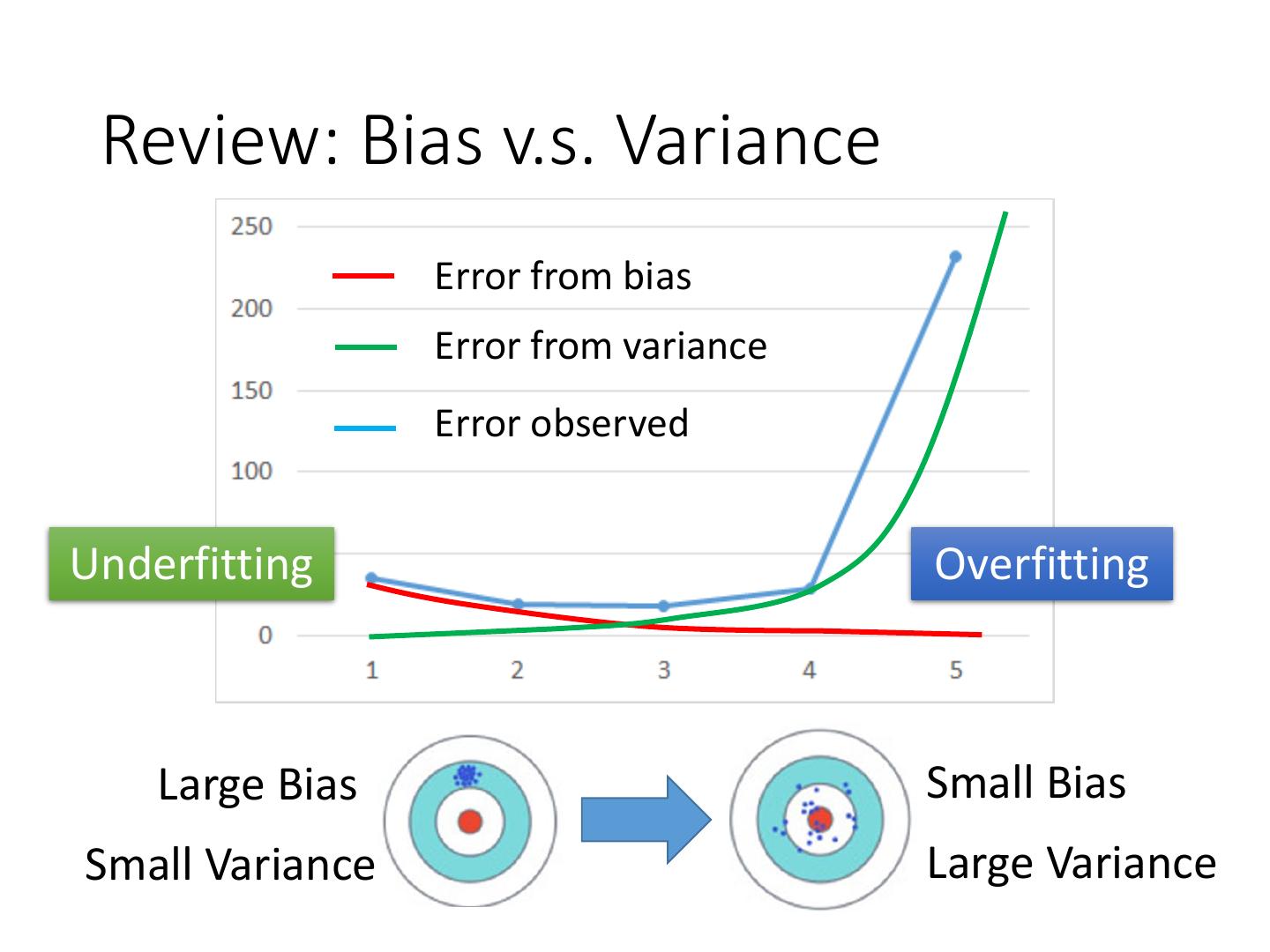
4 . Review: Bias v.s. Variance Error from bias Error from variance Error observed Underfitting Overfitting Large Bias Small Bias Small Variance Large Variance 

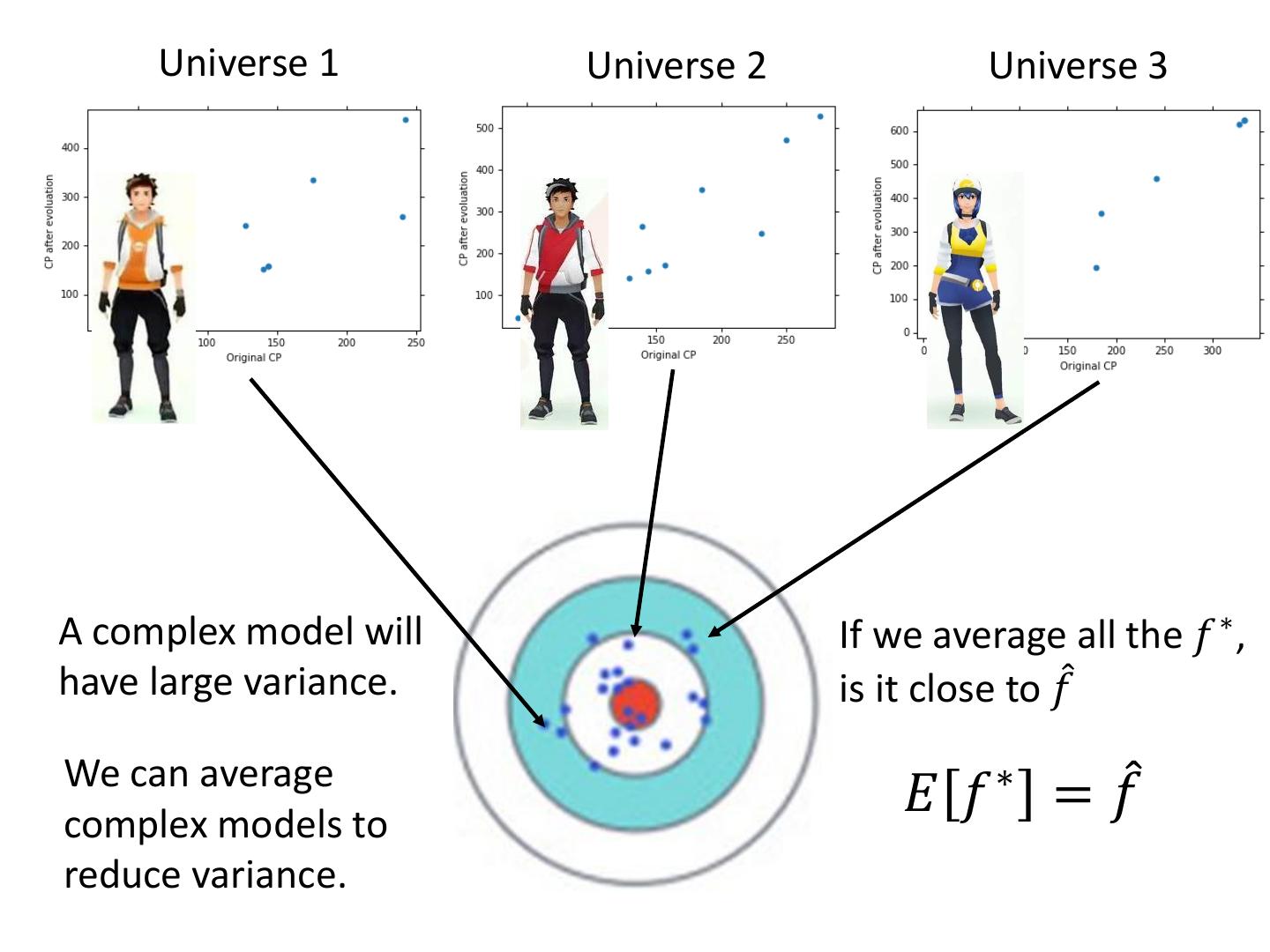
5 . Universe 1 Universe 2 Universe 3 A complex model will If we average all the 𝑓 ∗ , have large variance. is it close to 𝑓መ We can average complex models to 𝐸 𝑓 ∗ = 𝑓መ reduce variance. 

6 . Sampling N’ N training examples with Bagging examples replacement (usually N=N’) Set 1 Set 2 Set 3 Set 4 Function Function Function Function 1 2 3 4 

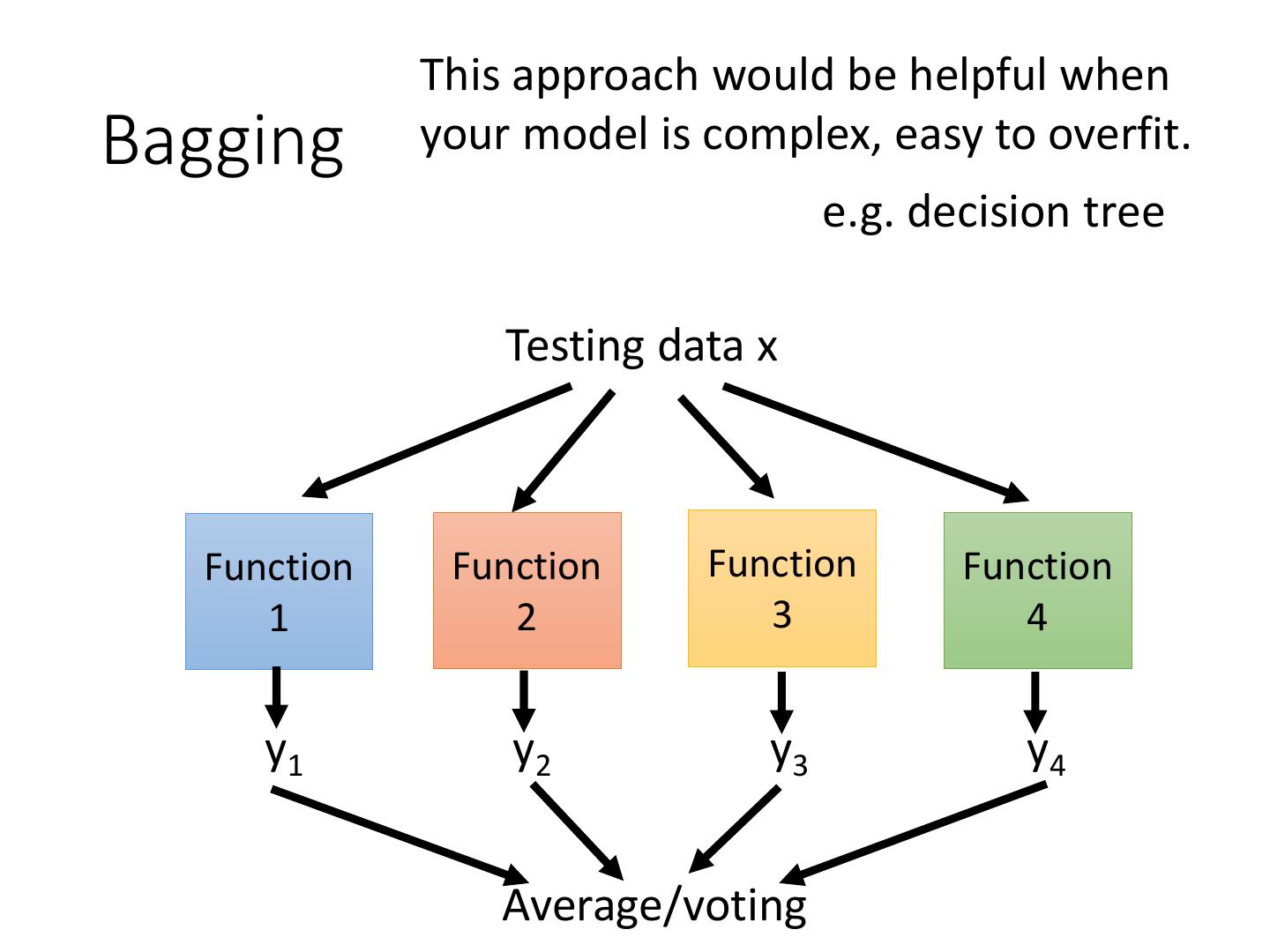
7 . This approach would be helpful when Bagging your model is complex, easy to overfit. e.g. decision tree Testing data x Function Function Function Function 1 2 3 4 y1 y2 y3 y4 Average/voting 

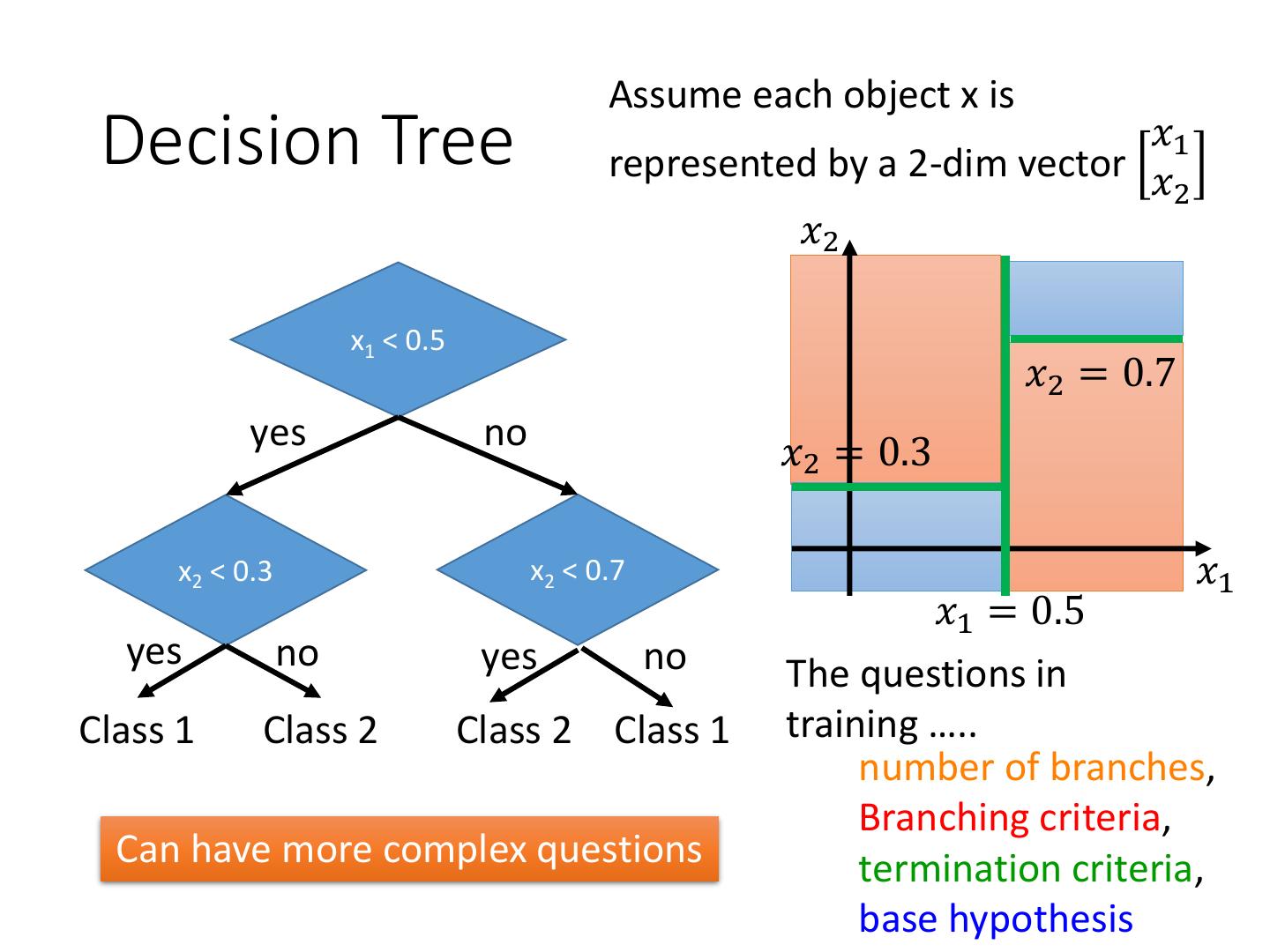
8 . Assume each object x is Decision Tree 𝑥1 represented by a 2-dim vector 𝑥 2 𝑥2 x1 < 0.5 𝑥2 = 0.7 yes no 𝑥2 = 0.3 x2 < 0.3 x2 < 0.7 𝑥1 𝑥1 = 0.5 yes no yes no The questions in Class 1 Class 2 Class 2 Class 1 training ….. number of branches, Branching criteria, Can have more complex questions termination criteria, base hypothesis 

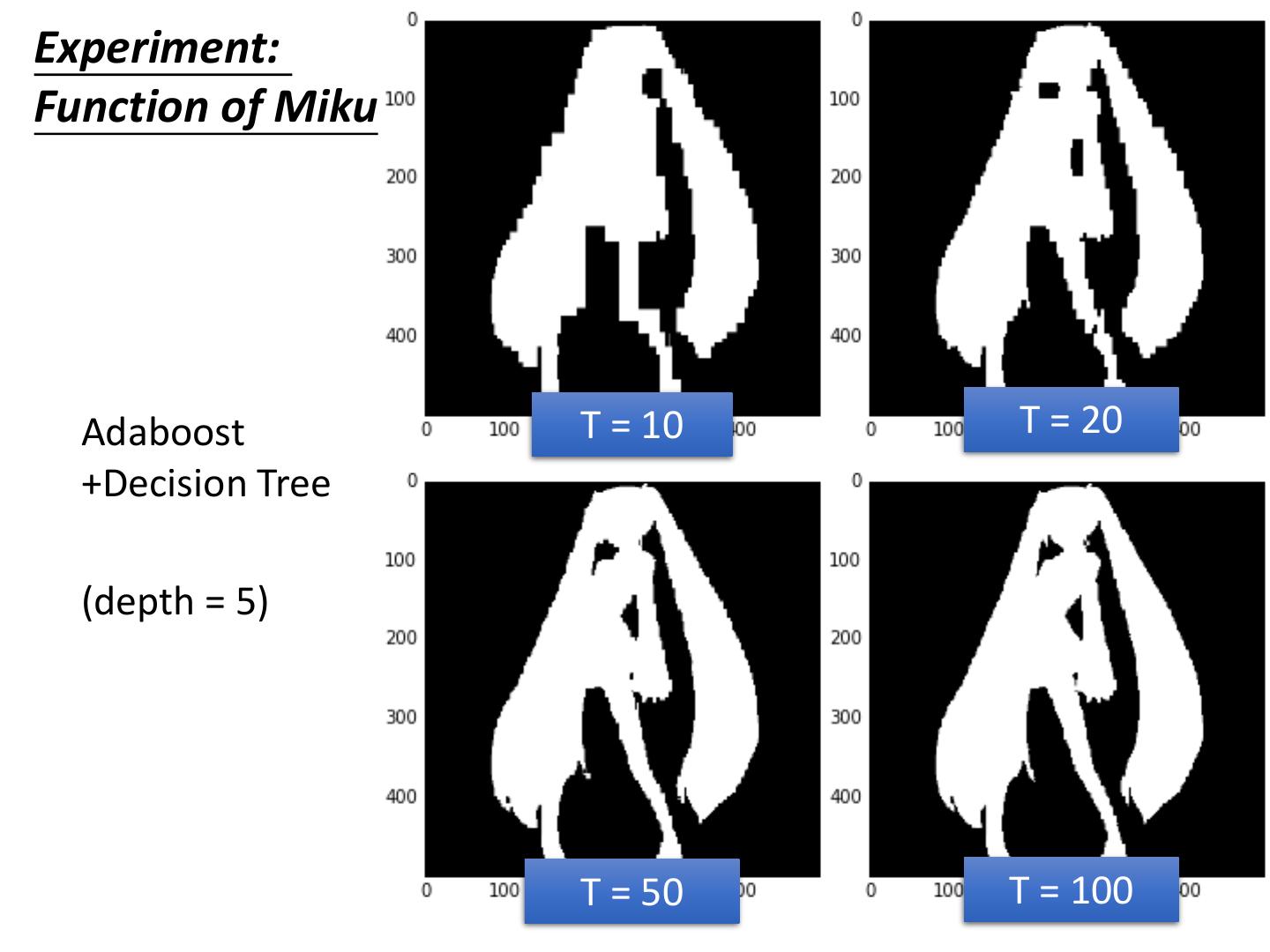
9 .Experiment: Function of Miku 0 1 http://speech.ee.ntu.edu.tw/~tlkagk/courses/ MLDS_2015_2/theano/miku (1st column: x, 2nd column: y, 3rd column: output (1 or 0) ) 

10 .Experiment: Function of Miku Single Depth = 5 Depth = 10 Decision Tree Depth = 15 Depth = 20 

11 . train f1 f2 f3 f4 x1 O X O X Random Forest x2 O X X O x3 X O O X • Decision tree: x4 X O X O • Easy to achieve 0% error rate on training data • If each training example has its own leaf …… • Random forest: Bagging of decision tree • Resampling training data is not sufficient • Randomly restrict the features/questions used in each split • Out-of-bag validation for bagging • Using RF = f2+f4 to test x1 • Using RF = f2+f3 to test x2 Out-of-bag (OOB) error • Using RF = f1+f4 to test x3 Good error estimation • Using RF = f1+f3 to test x4 of testing set 

12 .Experiment: Function of Miku Random Forest Depth = 5 Depth = 10 (100 trees) Depth = 15 Depth = 20 

13 .Ensemble: Boosting Improving Weak Classifiers 

14 . Training data: 𝑥 1 , 𝑦ො 1 , ⋯ , 𝑥 𝑛 , 𝑦ො 𝑛 , ⋯ , 𝑥 𝑁 , 𝑦ො 𝑁 Boosting 𝑦ො = ±1 (binary classification) • Guarantee: • If your ML algorithm can produce classifier with error rate smaller than 50% on training data • You can obtain 0% error rate classifier after boosting. • Framework of boosting • Obtain the first classifier 𝑓1 𝑥 • Find another function 𝑓2 𝑥 to help 𝑓1 𝑥 • However, if 𝑓2 𝑥 is similar to 𝑓1 𝑥 , it will not help a lot. • We want 𝑓2 𝑥 to be complementary with 𝑓1 𝑥 (How?) • Obtain the second classifier 𝑓2 𝑥 • …… Finally, combining all the classifiers • The classifiers are learned sequentially. 

15 .How to obtain different classifiers? • Training on different training data sets • How to have different training data sets • Re-sampling your training data to form a new set • Re-weighting your training data to form a new set • In real implementation, you only have to change the cost/objective function 𝑥 1 , 𝑦ො 1 , 𝑢1 𝑢1 = 1 0.4 𝐿 𝑓 = ෍ 𝑙 𝑓 𝑥 𝑛 , 𝑦ො 𝑛 𝑛 𝑥 2 , 𝑦ො 2 , 𝑢2 𝑢2 =1 2.1 𝐿 𝑓 = ෍ 𝑢𝑛 𝑙 𝑓 𝑥 𝑛 , 𝑦ො 𝑛 𝑥 3 , 𝑦ො 3 , 𝑢3 𝑢3 = 1 0.7 𝑛 

16 .Idea of Adaboost • Idea: training 𝒇𝟐 𝒙 on the new training set that fails 𝒇𝟏 𝒙 • How to find a new training set that fails 𝑓1 𝑥 ? 𝜀1 : the error rate of 𝑓1 𝑥 on its training data σ𝑛 𝑢1𝑛 𝛿 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝜀1 = 𝑍1 = ෍ 𝑢1𝑛 𝜀1 < 0.5 𝑍1 𝑛 Changing the example weights from 𝑢1𝑛 to 𝑢2𝑛 such that σ𝑛 𝑢2𝑛 𝛿 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 The performance of 𝑓1 for new = 0.5 weights would be random. 𝑍2 Training 𝑓2 𝑥 based on the new weights 𝑢2𝑛 

17 . Re-weighting Training Data • Idea: training 𝒇𝟐 𝒙 on the new training set that fails 𝒇𝟏 𝒙 • How to find a new training set that fails 𝑓1 𝑥 ? 𝑥 1 , 𝑦ො 1 , 𝑢1 𝑢1 = 1 𝑢1 = 1/ 3 𝑥 2 , 𝑦ො 2 , 𝑢2 𝑢2 = 1 𝑢2 = 3 3 3 𝑥 , 𝑦ො , 𝑢 3 𝑢3 = 1 𝑢3 = 1/ 3 𝑥 4 , 𝑦ො 4 , 𝑢4 4 𝑢 =1 𝑢4 = 1/ 3 𝜀2 <0.5 𝜀1 =0.25 0.5 𝑓1 𝑥 𝑓2 𝑥 

18 .Re-weighting Training Data • Idea: training 𝒇𝟐 𝒙 on the new training set that fails 𝒇𝟏 𝒙 • How to find a new training set that fails 𝑓1 𝑥 ? If 𝑥 𝑛 misclassified by 𝑓1 (𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 ) 𝑢2𝑛 ← 𝑢1𝑛 multiplying 𝑑1 increase If 𝑥 𝑛 correctly classified by 𝑓1 (𝑓1 𝑥 𝑛 = 𝑦ො 𝑛 ) 𝑢2𝑛 ← 𝑢1𝑛 divided by 𝑑1 decrease 𝑓2 will be learned based on example weights 𝑢2𝑛 What is the value of 𝑑1 ? 

19 .Re-weighting Training Data σ𝑛 𝑢1𝑛 𝛿 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝜀1 = 𝑍1 = ෍ 𝑢1𝑛 𝑍1 𝑛 σ𝑛 𝑢2𝑛 𝛿 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝑢2𝑛 ← 𝑢1𝑛 multiplying 𝑑1 = 0.5 𝑍2 𝑓1 𝑥 𝑛 = 𝑦ො 𝑛 𝑢2𝑛 ← 𝑢1𝑛 divided by 𝑑1 = ෍ 𝑢1𝑛 𝑑1 = ෍ 𝑢2𝑛 + ෍ 𝑢2𝑛 𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 𝑓1 𝑥 𝑛 =𝑦ො 𝑛 = ෍ 𝑢2𝑛 = ෍ 𝑢1𝑛 𝑑1 + ෍ 𝑢1𝑛 /𝑑1 𝑛 𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 𝑓1 𝑥 𝑛 =𝑦ො 𝑛 σ𝑓1 𝑛 𝑥𝑛 ො ≠𝑦 𝑛 𝑢1 𝑑1 = 0.5 2 σ𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 𝑢1𝑛 𝑑1 + σ𝑓1 𝑥 𝑛 =𝑦ො 𝑛 𝑢1𝑛 /𝑑1 

20 .Re-weighting Training Data σ𝑛 𝑢1𝑛 𝛿 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝜀1 = 𝑍1 = ෍ 𝑢1𝑛 𝑍1 𝑛 σ𝑛 𝑢2𝑛 𝛿 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝑓1 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝑢2𝑛 ← 𝑢1𝑛 multiplying 𝑑1 = 0.5 𝑍2 𝑓1 𝑥 𝑛 = 𝑦ො 𝑛 𝑢2𝑛 ← 𝑢1𝑛 divided by 𝑑1 σ𝑓1 𝑥𝑛 =𝑦ො 𝑛 𝑢1𝑛 /𝑑1 𝑛 =1 σ𝑓1 𝑛 𝑥 ≠𝑦ො 𝑛 𝑢1 𝑑1 1 ෍ 𝑢1𝑛 /𝑑1 = ෍ 𝑢1𝑛 𝑑1 ෍ 𝑢1𝑛 = 𝑑1 ෍ 𝑢1𝑛 𝑑1 𝑓1 𝑥 𝑛 =𝑦ො 𝑛 𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 𝑓1 𝑥 𝑛 =𝑦ො 𝑛 𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 σ𝑓1 𝑢1𝑛 𝑍1 1 − 𝜀1 𝑍1 𝜀1 𝑥𝑛 ≠𝑦ො 𝑛 𝜀1 = 𝑍1 𝑍1 1 − 𝜀1 /𝑑1 = 𝑍1 𝜀1 𝑑1 ෍ 𝑢1𝑛 = 𝑍1 𝜀1 𝑓1 𝑥 𝑛 ≠𝑦ො 𝑛 𝑑1 = 1 − 𝜀1 Τ𝜀1 > 1 

21 .Algorithm for AdaBoost • Giving training data 𝑥 1 , 𝑦ො 1 , 𝑢11 , ⋯ , 𝑥 𝑛 , 𝑦ො 𝑛 , 𝑢1𝑛 , ⋯ , 𝑥 𝑁 , 𝑦ො 𝑁 , 𝑢1𝑁 • 𝑦ො = ±1 (Binary classification), 𝑢1𝑛 = 1 (equal weights) • For t = 1, …, T: • Training weak classifier 𝑓𝑡 𝑥 with weights 𝑢𝑡1 , ⋯ , 𝑢𝑡𝑁 • 𝜀𝑡 is the error rate of 𝑓𝑡 𝑥 with weights 𝑢𝑡1 , ⋯ , 𝑢𝑡𝑁 • For n = 1, …, N: • If 𝑥 𝑛 is misclassified by 𝑓𝑡 𝑥 : 𝑦ො 𝑛 ≠ 𝑓𝑡 𝑥 𝑛 • 𝑢𝑡+1 𝑛 = 𝑢𝑡𝑛 × 𝑑𝑡 = 𝑢𝑡𝑛 × 𝑒xp 𝛼𝑡 𝑑𝑡 = 1 − 𝜀𝑡 Τ𝜀𝑡 • Else: 𝑛 𝑛 𝑛 𝛼𝑡 = 𝑙𝑛 1 − 𝜀𝑡 Τ𝜀𝑡 • 𝑢𝑡+1 = 𝑢𝑡 /𝑑𝑡 = 𝑢𝑡 × 𝑒xp −𝛼𝑡 𝑛 𝑢𝑡+1 ← 𝑢𝑡𝑛 × 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑓𝑡 𝑥 𝑛 𝛼𝑡 

22 .Algorithm for AdaBoost • We obtain a set of functions: 𝑓1 𝑥 , … , 𝑓𝑡 𝑥 , … , 𝑓𝑇 𝑥 • How to aggregate them? • Uniform weight: • 𝐻 𝑥 = 𝑠𝑖𝑔𝑛 σ𝑇𝑡=1 𝑓𝑡 𝑥 Smaller error 𝜀𝑡 , • Non-uniform weight: larger weight for 𝑇 final voting • 𝐻 𝑥 = 𝑠𝑖𝑔𝑛 σ𝑡=1 𝛼𝑡 𝑓𝑡 𝑥 𝛼𝑡 = 𝑙𝑛 1 − 𝜀𝑡 Τ𝜀𝑡 𝜀𝑡 = 0.1 𝜀𝑡 = 0.4 𝑛 𝑢𝑡+1 = 𝑢𝑡𝑛 × 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑓𝑡 𝑥 𝑛 𝛼𝑡 𝛼𝑡 =1.10 𝛼𝑡 =0.20 

23 .Toy Example T=3, weak classifier = decision stump • t=1 1.0 + 1.0 + 1.0 - 1.53 + + 1.53 0.65 - 1.0 + 1.53 + 1.0 + - - 0.65 + - - 1.0 1.0 0.65 0.65 𝜀1 = 0.30 1.0 + 1.0 - 0.65 + 0.65 - 1.0 - 𝑑1 = 1.53 0.65 - 𝛼1 = 0.42 𝑓1 𝑥 

24 .Toy Example T=3, weak classifier = decision stump 𝑓1 𝑥 : • t=2 𝛼1 = 0.42 1.53 + + 1.53 0.65 - 0.78 + 0.78 + 0.33 - 1.53 + 0.78 + 1.26- 1.26 - - 0.33 + 0.65 + - 0.65 0.65 𝜀2 = 0.21 0.33 + 0.33 - 0.65 + 0.65 - 0.65 - 𝑑2 = 1.94 1.26 - 𝛼2 = 0.66 𝑓2 𝑥 

25 . Toy Example T=3, weak classifier = decision stump 𝑓1 𝑥 : 𝑓2 𝑥 : • t=3 𝛼1 = 0.42 𝛼2 = 0.66 0.78 + 0.33 - 𝑓3 𝑥 : 0.78 + 0.78 + 𝛼3 = 0.95 𝑓3 𝑥 1.26- 1.26 - 0.33 + 𝜀3 = 0.13 0.33 + 0.33 - 𝑑3 = 2.59 1.26 - 𝛼3 = 0.95 

26 . Toy Example • Final Classifier: 𝐻 𝑥 = 𝑠𝑖𝑔𝑛 σ𝑇𝑡=1 𝛼𝑡 𝑓𝑡 𝑥 𝑠𝑖𝑔𝑛( 0.42 + 0.66 + 0.95 ) + + - + + - - + - - 

27 . Warning of Math 𝑇 𝐻 𝑥 = 𝑠𝑖𝑔𝑛 ෍ 𝛼𝑡 𝑓𝑡 𝑥 𝛼𝑡 = 𝑙𝑛 1 − 𝜀𝑡 Τ𝜀𝑡 𝑡=1 As we have more and more 𝑓𝑡 (T increases), 𝐻 𝑥 achieves smaller and smaller error rate on training data. 

28 .Error Rate of Final Classifier • Final classifier: 𝐻 𝑥 = 𝑠𝑖𝑔𝑛 σ𝑇𝑡=1 𝛼𝑡 𝑓𝑡 𝑥 • 𝛼𝑡 = 𝑙𝑛 1 − 𝜀𝑡 Τ𝜀𝑡 𝑔 𝑥 Training Data Error Rate 1 = ෍ 𝛿 𝐻 𝑥 𝑛 ≠ 𝑦ො 𝑛 𝑁 𝑛 1 = ෍ 𝛿 𝑦ො 𝑛 𝑔 𝑥 𝑛 <0 𝑁 𝑛 1 ≤ ෍ 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑔 𝑥 𝑛 𝑁 𝑛 𝑦ො 𝑛 𝑔 𝑥 𝑛 

29 . 𝑇 Training Data Error Rate 𝑔 𝑥 = ෍ 𝛼𝑡 𝑓𝑡 𝑥 1 1 𝑡=1 ≤ ෍ 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑔 𝑥 𝑛 = 𝑍𝑇+1 𝑁 𝑁 𝛼𝑡 = 𝑙𝑛 1 − 𝜀𝑡 Τ𝜀𝑡 𝑛 𝑍𝑡 : the summation of the weights of training data for training 𝑓𝑡 What is 𝑍𝑇+1 =? 𝑍𝑇+1 = ෍ 𝑢𝑛𝑇+1 𝑛 𝑇 𝑢1𝑛 =1 𝑢𝑛𝑇+1 = ෑ 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑓𝑡 𝑥 𝑛 𝛼𝑡 𝑛 𝑢𝑡+1 = 𝑢𝑡𝑛 × 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑓𝑡 𝑥 𝑛 𝛼𝑡 𝑡=1 𝑇 𝑍𝑇+1 = ෍ ෑ 𝑒𝑥𝑝 −𝑦ො 𝑛 𝑓𝑡 𝑥 𝑛 𝛼𝑡 𝑇 𝑔 𝑥 𝑛 𝑡=1 = ෍ 𝑒𝑥𝑝 −𝑦ො 𝑛 ෍ 𝑓𝑡 𝑥 𝑛 𝛼𝑡 𝑛 𝑡=1