Bias and Variance

1 .Where does the error come from? 

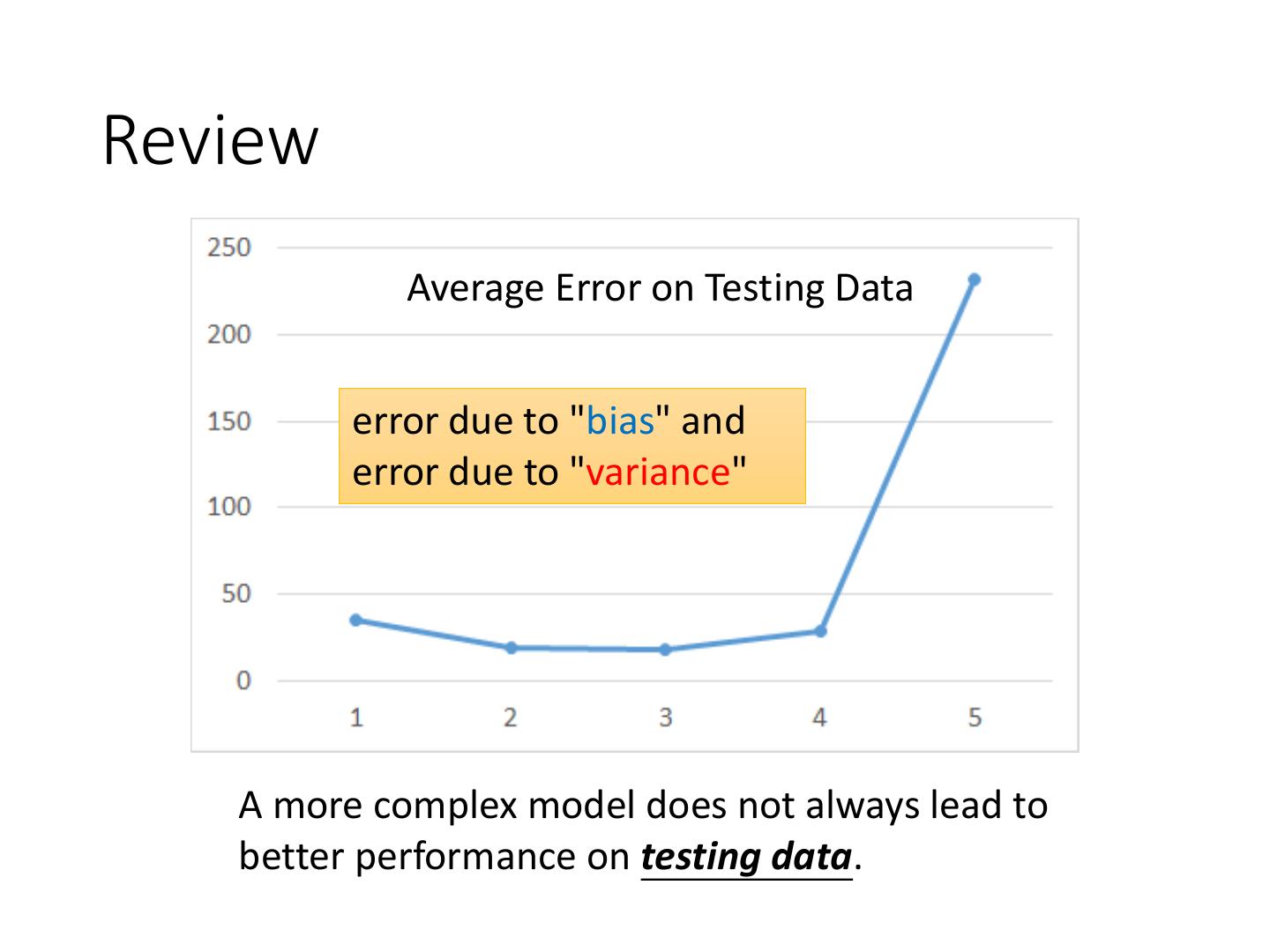
2 .Review Average Error on Testing Data error due to "bias" and error due to "variance" A more complex model does not always lead to better performance on testing data. 

3 .Estimator 𝑓∗ 𝑦ො = 𝑓መ Bias + Variance Only Niantic knows 𝑓መ From training data, we find 𝑓 ∗ 𝑓መ 𝑓 ∗ is an estimator of 𝑓መ 

4 .Bias and Variance of Estimator unbiased • Estimate the mean of a variable x • assume the mean of x is 𝜇 𝑚2 • assume the variance of x is 𝜎 2 • Estimator of mean 𝜇 𝑚5 • Sample N points: 𝑥 1 , 𝑥 2 , … , 𝑥 𝑁 𝑚1 𝜇 1 𝑚 = ෍ 𝑥𝑛 ≠ 𝜇 𝑚4 𝑁 𝑛 𝑚3 1 𝑛 1 𝐸 𝑚 =𝐸 ෍ 𝑥 = ෍ 𝐸 𝑥𝑛 = 𝜇 𝑁 𝑁 𝑛 𝑛 𝑚6 

5 .Bias and Variance of Estimator unbiased • Estimate the mean of a variable x • assume the mean of x is 𝜇 Smaller N Larger N • assume the variance of x is 𝜎 2 • Estimator of mean 𝜇 • Sample N points: 𝑥 1 , 𝑥 2 , … , 𝑥 𝑁 1 𝑚 = ෍ 𝑥𝑛 ≠ 𝜇 𝑁 𝜇 𝜇 𝑛 Variance depends 𝜎2 V𝑎𝑟 𝑚 = on the number of 𝑁 samples 

6 .Bias and Variance of Estimator Increase N • Estimate the mean of a variable x • assume the mean of x is 𝜇 • assume the variance of x is 𝜎 2 • Estimator of variance 𝜎 2 𝑠3 • Sample N points: 𝑥 1 , 𝑥 2 , … , 𝑥 𝑁 𝜎2 𝜎2 𝑠1 1 1 𝑚 = ෍ 𝑥 𝑠 = ෍ 𝑥𝑛 − 𝑚 𝑛 2 𝑠4 𝑁 𝑁 𝑛 𝑛 𝑠5 Biased estimator 𝑠2 𝑁−1 2 𝑠6 𝐸𝑠 = 𝜎 ≠ 𝜎2 𝑁 

7 .𝐸 𝑓 ∗ = 𝑓ҧ 𝑓∗ Variance Bias 𝑓መ 

8 .Parallel Universes • In all the universes, we are collecting (catching) 10 Pokémons as training data to find 𝑓 ∗ Universe 1 Universe 2 Universe 3 

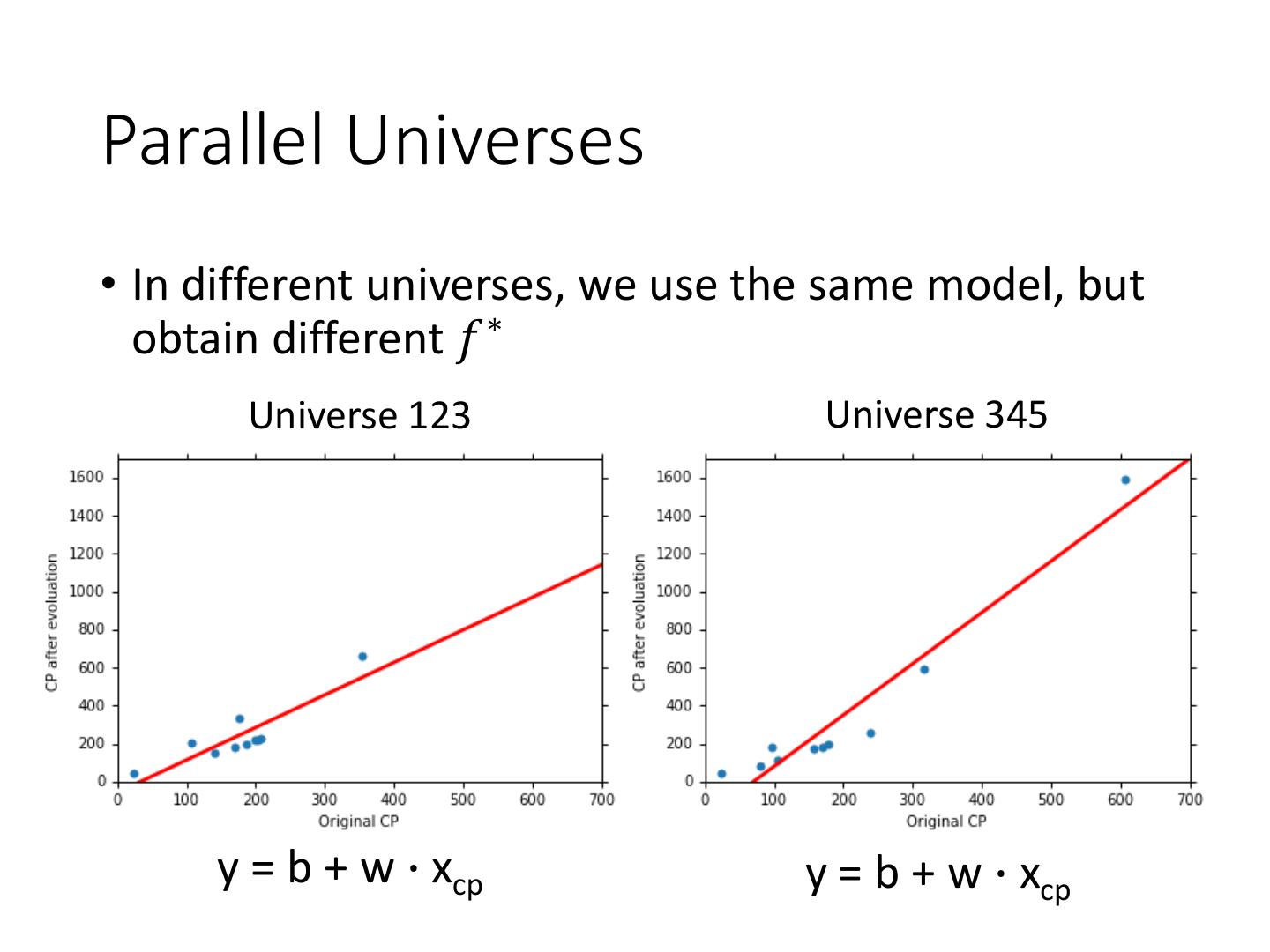
9 .Parallel Universes • In different universes, we use the same model, but obtain different 𝑓 ∗ Universe 123 Universe 345 y = b + w ∙ xcp y = b + w ∙ xcp 

10 .𝑓 ∗ in 100 Universes y = b + w ∙ xcp y = b + w1 ∙ xcp + w2 ∙ (xcp)2 + w3 ∙ (xcp)3 y = b + w1 ∙ xcp + w2 ∙ (xcp)2 + w3 ∙ (xcp)3 + w4 ∙ (xcp)4 + w5 ∙ (xcp)5 

11 . y = b + w1 ∙ xcp + w2 ∙ (xcp)2 Variance + w3 ∙ (xcp)3 + w4 ∙ (xcp)4 + w5 ∙ (xcp)5 y = b + w ∙ xcp Small Large Variance Variance Simpler model is less influenced by the sampled data Consider the extreme case f(x) = 5 

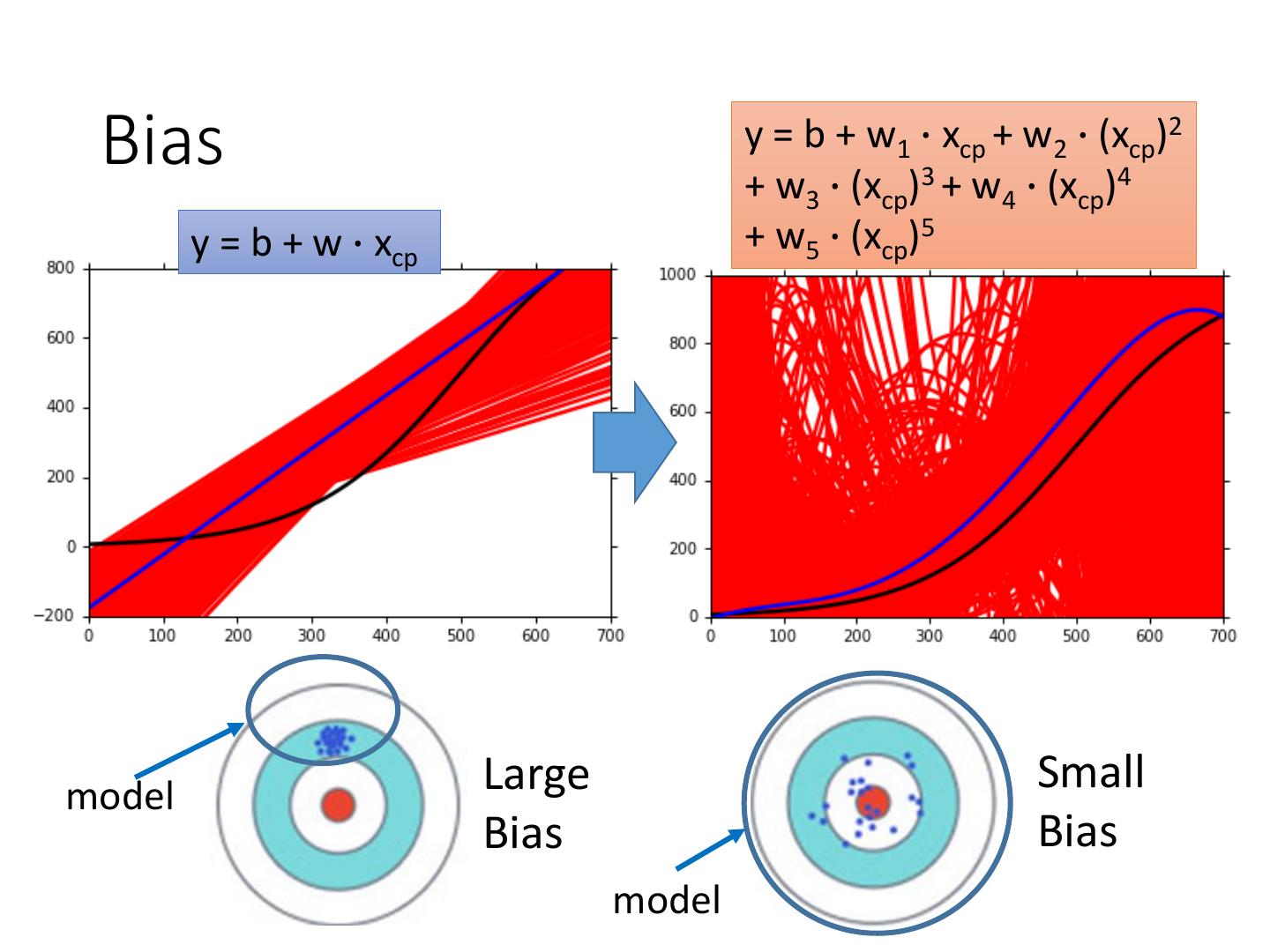
12 .Bias 𝐸 𝑓 ∗ = 𝑓ҧ • Bias: If we average all the 𝑓 ∗ , is it close to 𝑓መ ? Large Bias Assume this is 𝑓መ Small Bias 

13 .Black curve: the true function 𝑓መ Red curves: 5000 𝑓 ∗ Blue curve: the average of 5000 𝑓 ∗ = 𝑓ҧ 

14 . Bias y = b + w1 ∙ xcp + w2 ∙ (xcp)2 + w3 ∙ (xcp)3 + w4 ∙ (xcp)4 y = b + w ∙ xcp + w5 ∙ (xcp)5 model Large Small Bias Bias model 

15 . Bias v.s. Variance Error from bias Error from variance Error observed Underfitting Overfitting Large Bias Small Bias Small Variance Large Variance 

16 .What to do with large bias? • Diagnosis: • If your model cannot even fit the training examples, then you have large bias Underfitting • If you can fit the training data, but large error on testing data, then you probably have large variance Overfitting • For bias, redesign your model: large bias • Add more features as input • A more complex model 

17 . What to do with large variance? • More data Very effective, but not always practical 10 examples 100 examples • Regularization May increase bias 

18 .Model Selection • There is usually a trade-off between bias and variance. • Select a model that balances two kinds of error to minimize total error • What you should NOT do: Training Set Testing Set Real Testing Set Model 1 Err = 0.9 (not in hand) Model 2 Err = 0.7 Model 3 Err = 0.5 Err > 0.5 

19 .Homework public private Training Set Testing Set Testing Set Model 1 Err = 0.9 Model 2 Err = 0.7 Model 3 Err = 0.5 Err > 0.5 I beat baseline! No, you don’t What will happen? http://www.chioka.in/how- to-select-your-final-models- in-a-kaggle-competitio/ 

20 .Cross Validation public private Training Set Testing Set Testing Set Training Validation Using the results of public testing Set set data to tune your model You are making public set Model 1 Err = 0.9 better than private set. Model 2 Err = 0.7 Not recommend Model 3 Err = 0.5 Err > 0.5 Err > 0.5 

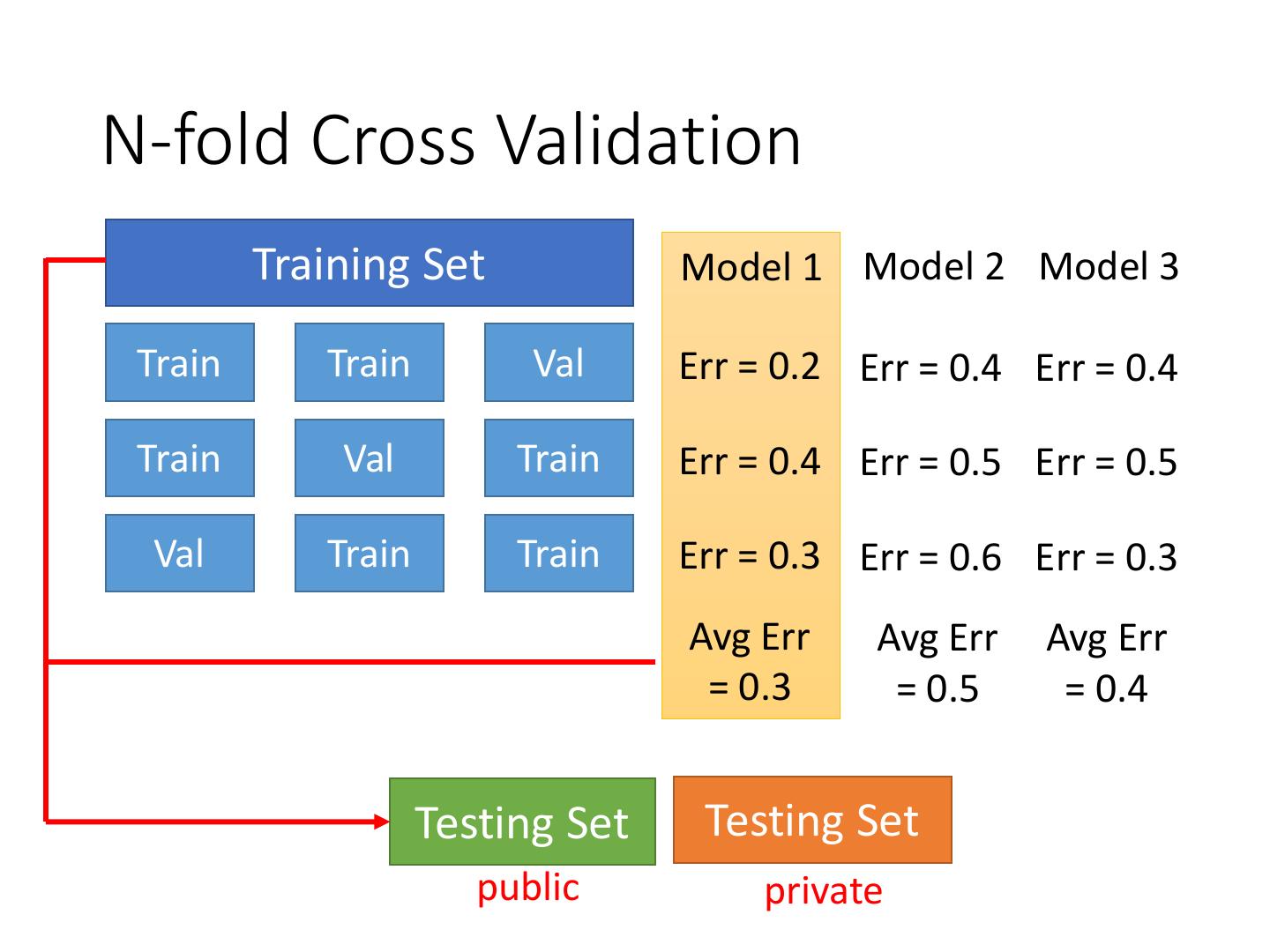
21 .N-fold Cross Validation Training Set Model 1 Model 2 Model 3 Train Train Val Err = 0.2 Err = 0.4 Err = 0.4 Train Val Train Err = 0.4 Err = 0.5 Err = 0.5 Val Train Train Err = 0.3 Err = 0.6 Err = 0.3 Avg Err Avg Err Avg Err = 0.3 = 0.5 = 0.4 Testing Set Testing Set public private 

22 .Reference • Bishop: Chapter 3.2