- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
Backpropagation
展开查看详情
1 .Backpropagation Hung-yi Lee 李宏毅
2 .Gradient Descent Network parameters w1 , w2 ,, b1 , b2 , Starting Parameters 0 1 2 …… L Compute L 0 1 0 L 0 L w1 L w Compute L 1 2 1 L 1 2 L b1 Millions of parameters …… L b2 To compute the gradients efficiently, we use backpropagation.
3 .Chain Rule Case 1 y g x z h y dz dz dy x y z dx dy dx Case 2 x g s y hs z k x, y x s dz z dx z dy z ds x ds y ds y
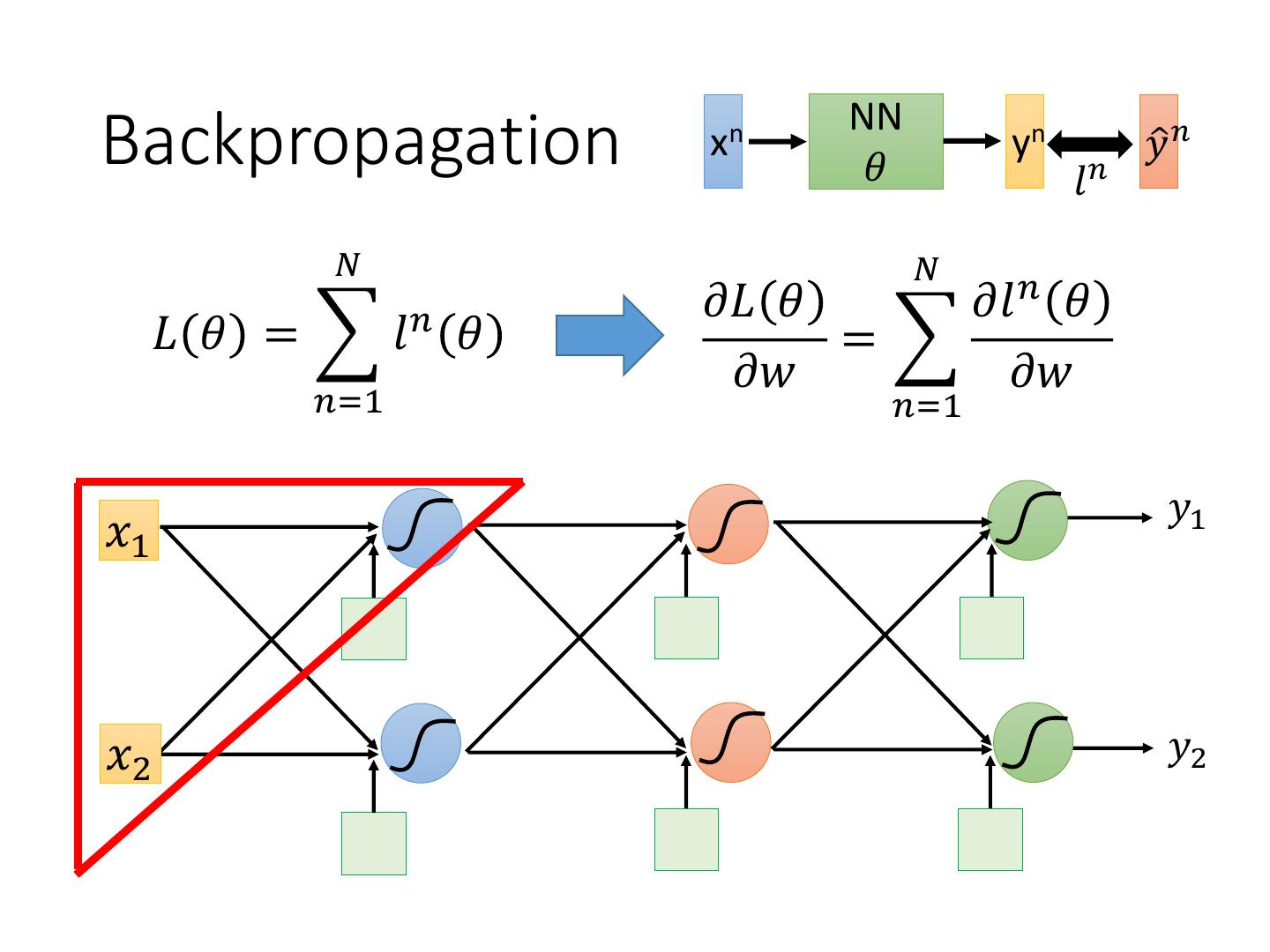
4 . NN Backpropagation xn 𝜃 yn 𝑙𝑛 𝑦ො 𝑛 𝑁 𝑁 𝜕𝐿 𝜃 𝜕𝑙 𝑛 𝜃 𝐿 𝜃 = 𝑙𝑛 𝜃 = 𝜕𝑤 𝜕𝑤 𝑛=1 𝑛=1 𝑦1 𝑥1 𝑥2 𝑦2
5 .Backpropagation 𝑤1 𝑧 𝑦1 𝑥1 …… 𝑤2 b 𝑧 = 𝑥1 𝑤1 + 𝑥2 𝑤2 + 𝑏 𝑥2 𝑦2 Forward pass: 𝜕𝑙 𝜕𝑧 𝜕𝑙 Compute 𝜕𝑧Τ𝜕𝑤 for all parameters =? 𝜕𝑤 𝜕𝑤 𝜕𝑧 Backward pass: (Chain rule) Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z
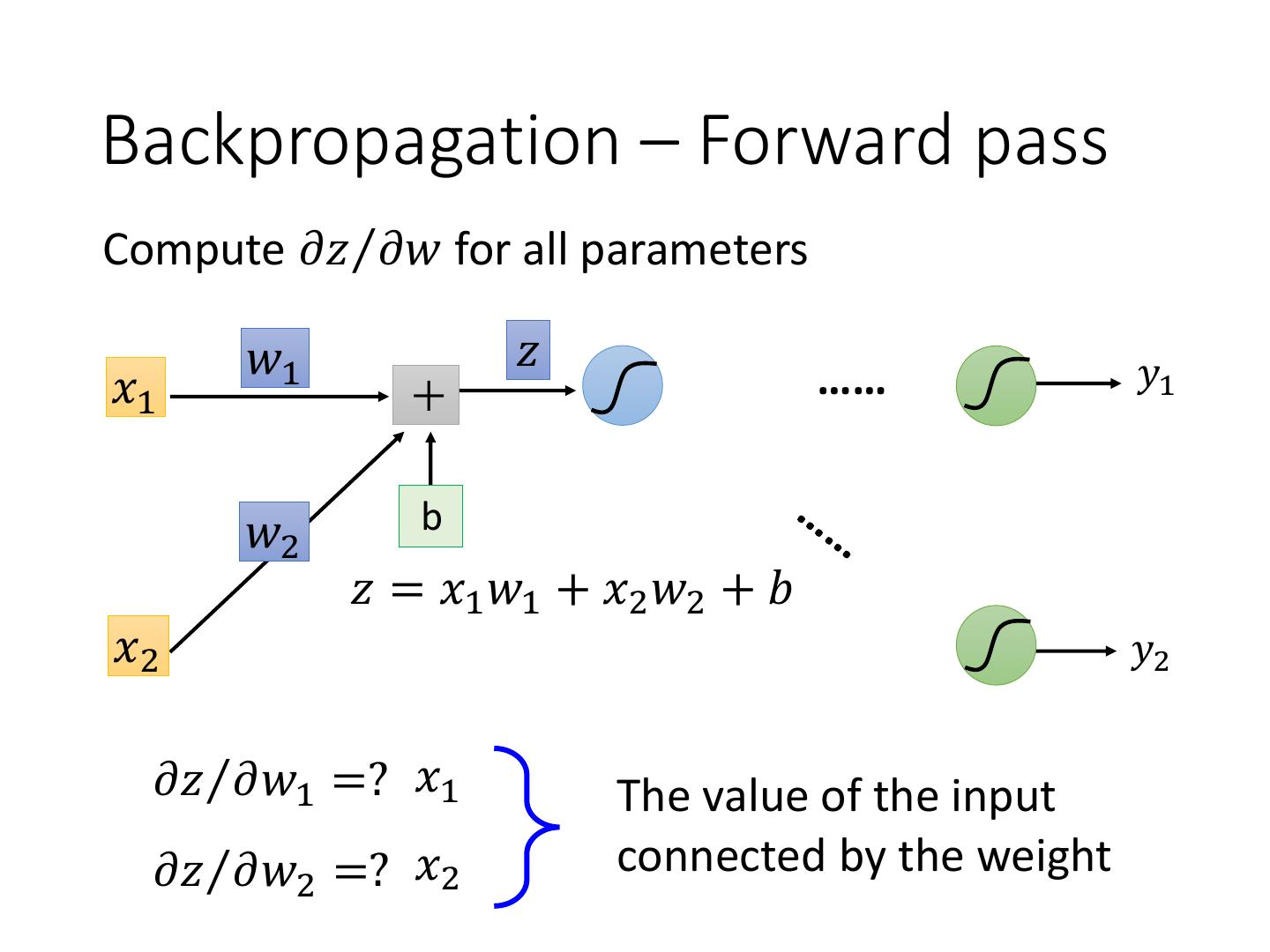
6 .Backpropagation – Forward pass Compute 𝜕𝑧Τ𝜕𝑤 for all parameters 𝑤1 𝑧 𝑦1 𝑥1 …… 𝑤2 b 𝑧 = 𝑥1 𝑤1 + 𝑥2 𝑤2 + 𝑏 𝑥2 𝑦2 𝜕𝑧Τ𝜕𝑤1 =? 𝑥1 The value of the input 𝜕𝑧Τ𝜕𝑤2 =? 𝑥2 connected by the weight
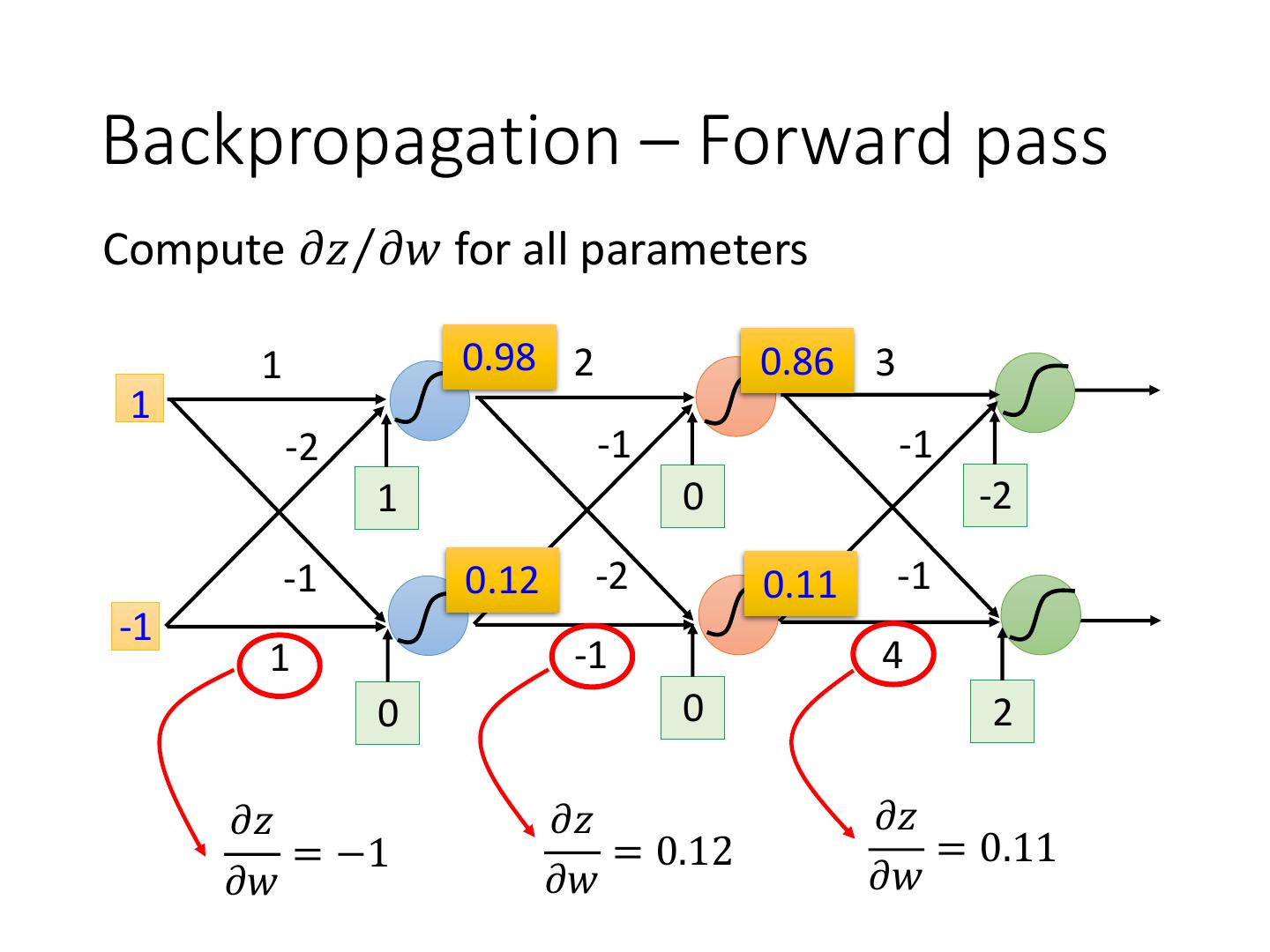
7 .Backpropagation – Forward pass Compute 𝜕𝑧Τ𝜕𝑤 for all parameters 1 0.98 2 0.86 3 1 -2 -1 -1 1 0 -2 -1 0.12 -2 0.11 -1 -1 1 -1 4 0 0 2 𝜕𝑧 𝜕𝑧 𝜕𝑧 = −1 = 0.12 = 0.11 𝜕𝑤 𝜕𝑤 𝜕𝑤
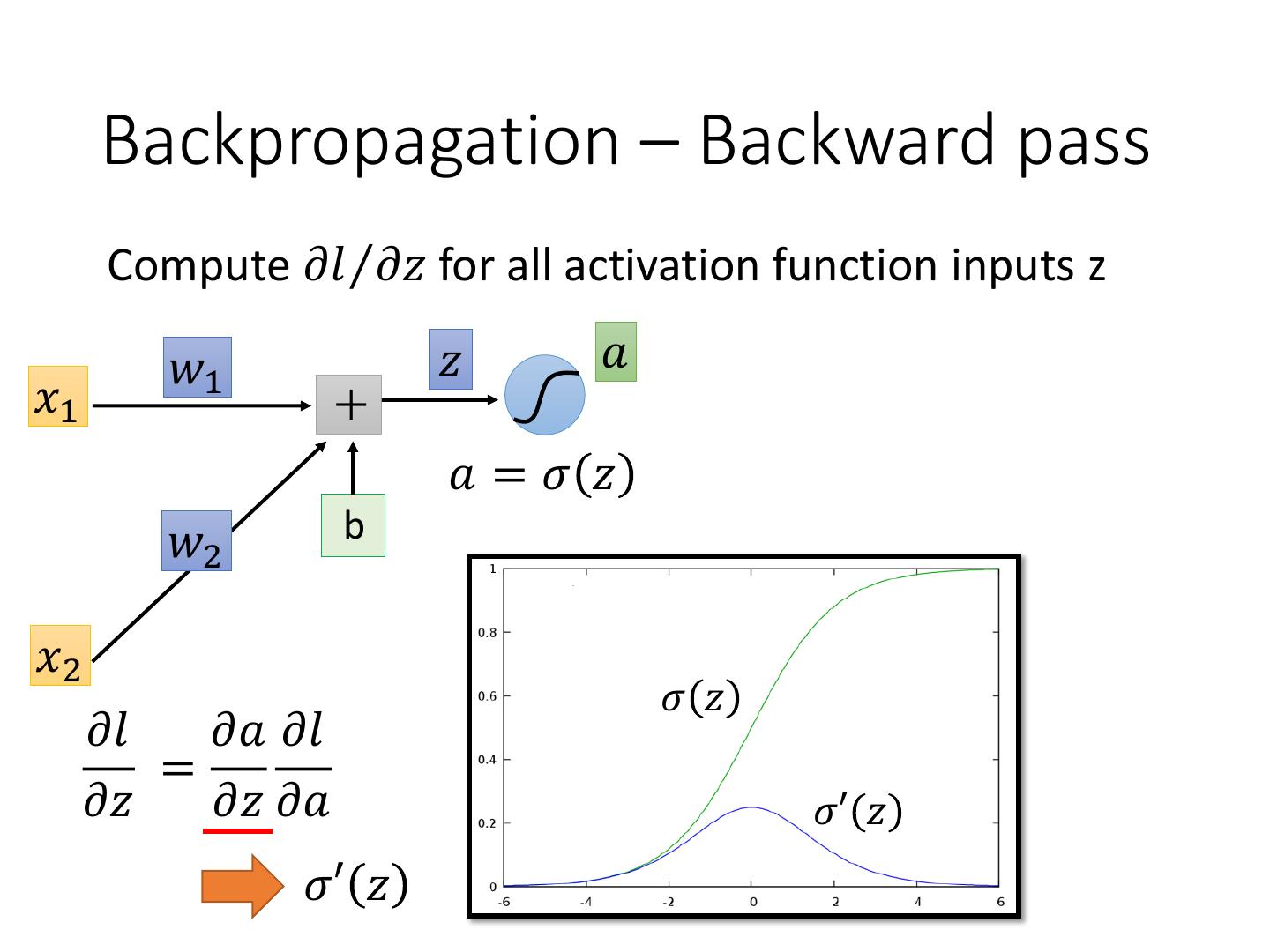
8 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z 𝑤1 𝑧 𝑎 𝑥1 𝑎=𝜎 𝑧 𝑤2 b 𝑥2 𝜎 𝑧 𝜕𝑙 𝜕𝑎 𝜕𝑙 = 𝜕𝑧 𝜕𝑧 𝜕𝑎 𝜎′ 𝑧 𝜎′ 𝑧
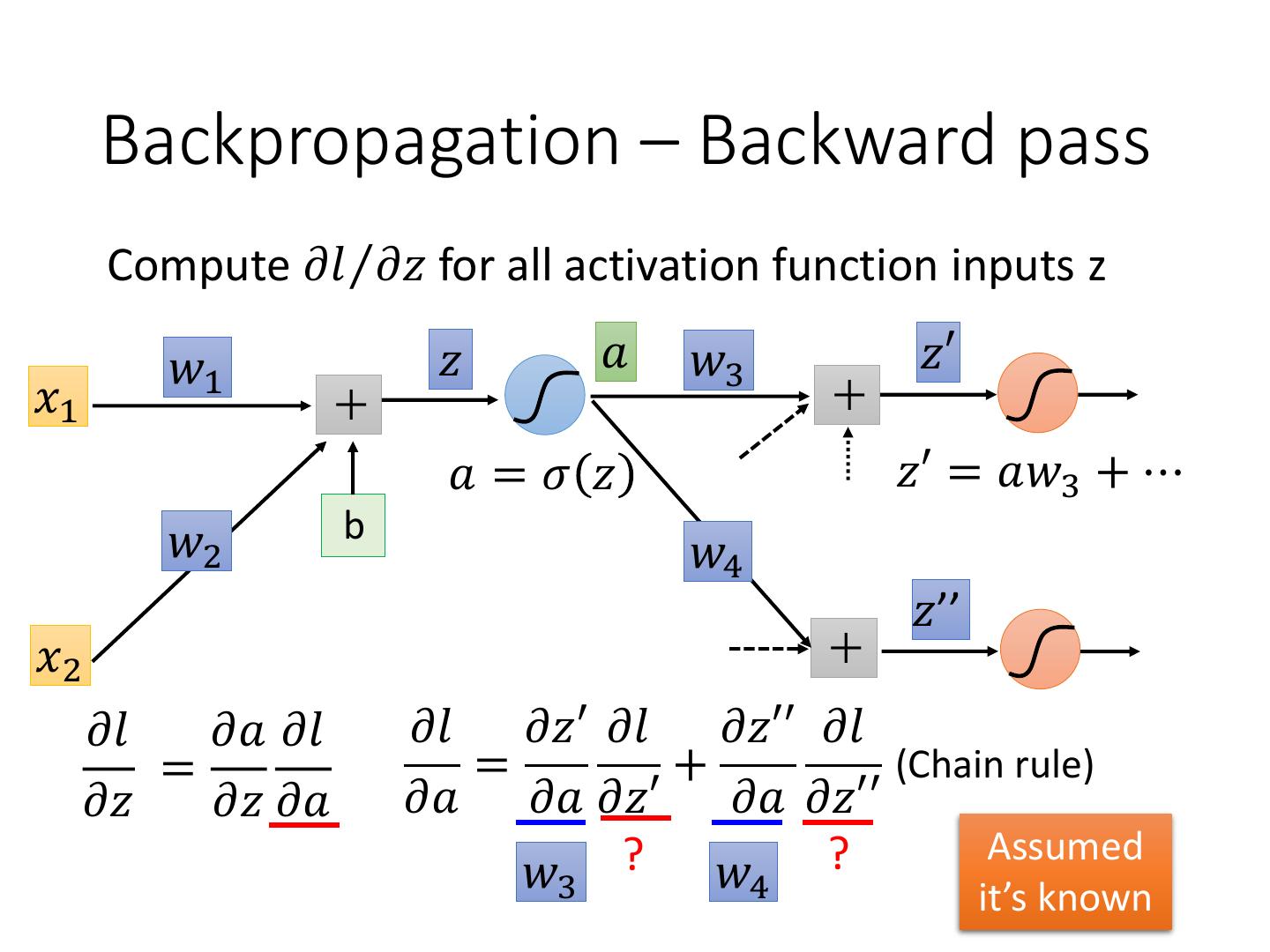
9 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z 𝑤1 𝑧 𝑎 𝑤3 𝑧′ 𝑥1 𝑎=𝜎 𝑧 𝑧′ = 𝑎𝑤3 + ⋯ 𝑤2 b 𝑤4 𝑧’’ 𝑥2 𝜕𝑙 𝜕𝑎 𝜕𝑙 𝜕𝑙 𝜕𝑧′ 𝜕𝑙 𝜕𝑧′′ 𝜕𝑙 = = + (Chain rule) 𝜕𝑧 𝜕𝑧 𝜕𝑎 𝜕𝑎 𝜕𝑎 𝜕𝑧′ 𝜕𝑎 𝜕𝑧′′ ? ? Assumed 𝑤 3 𝑤 4 it’s known
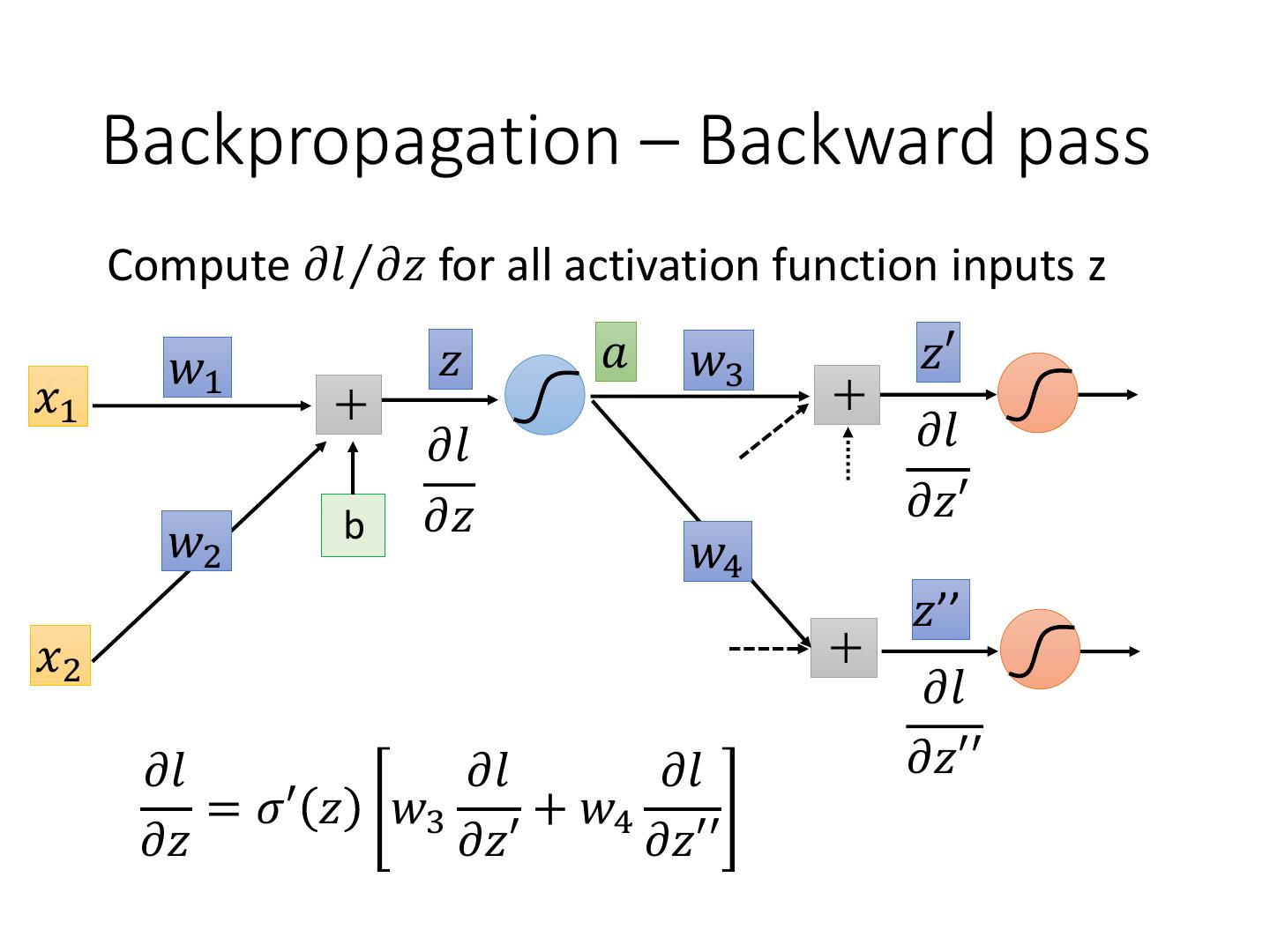
10 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z 𝑤1 𝑧 𝑎 𝑤3 𝑧′ 𝑥1 𝜕𝑙 𝜕𝑙 b 𝜕𝑧 𝜕𝑧′ 𝑤2 𝑤4 𝑧’’ 𝑥2 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑧′′ = 𝜎′ 𝑧 𝑤3 + 𝑤4 𝜕𝑧 𝜕𝑧′ 𝜕𝑧′′
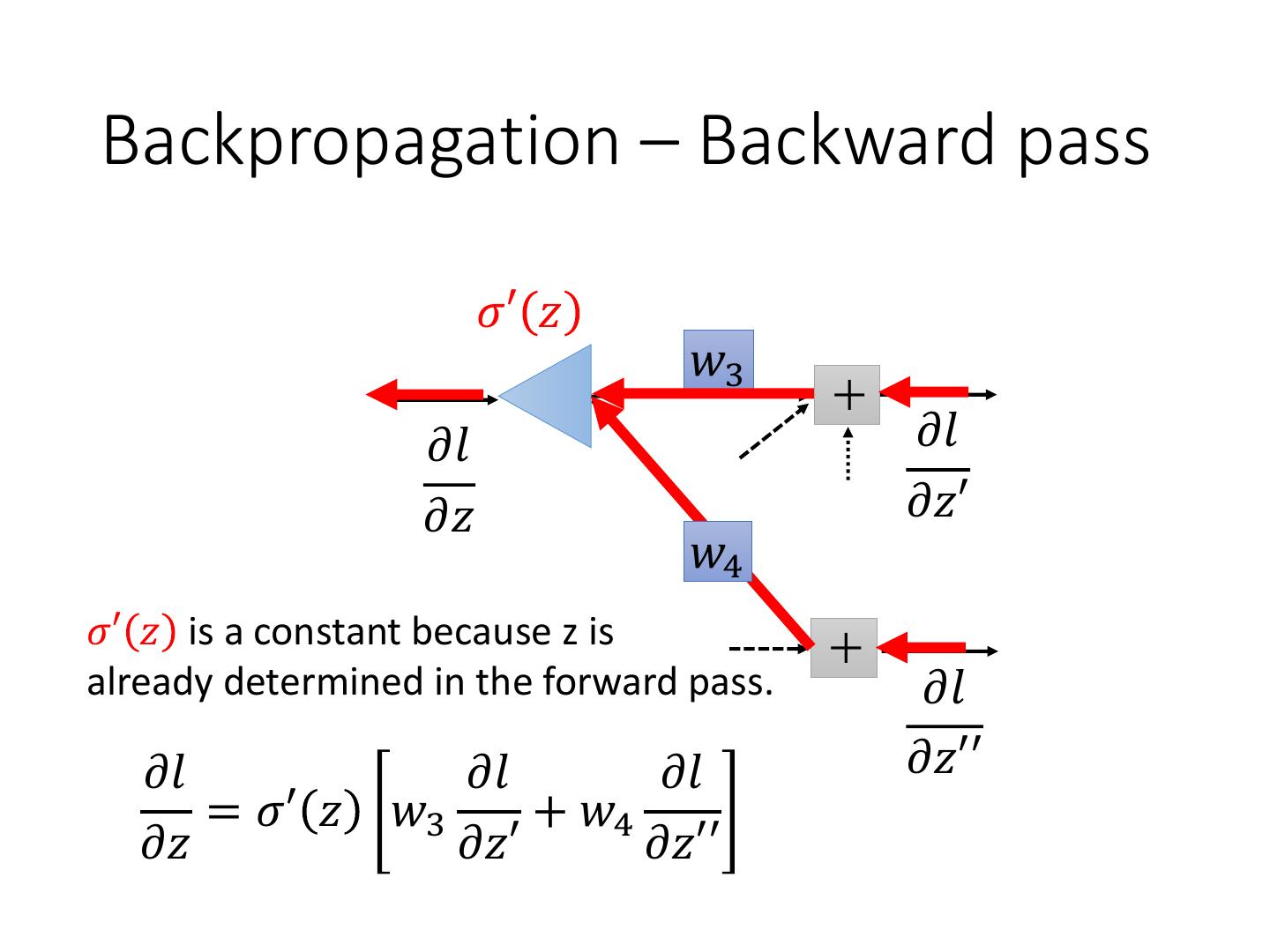
11 .Backpropagation – Backward pass 𝜎′ 𝑧 𝑤3 𝜕𝑙 𝜕𝑙 𝜕𝑧 𝜕𝑧′ 𝑤4 𝜎′ 𝑧 is a constant because z is already determined in the forward pass. 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑧′′ = 𝜎′ 𝑧 𝑤3 + 𝑤4 𝜕𝑧 𝜕𝑧′ 𝜕𝑧′′
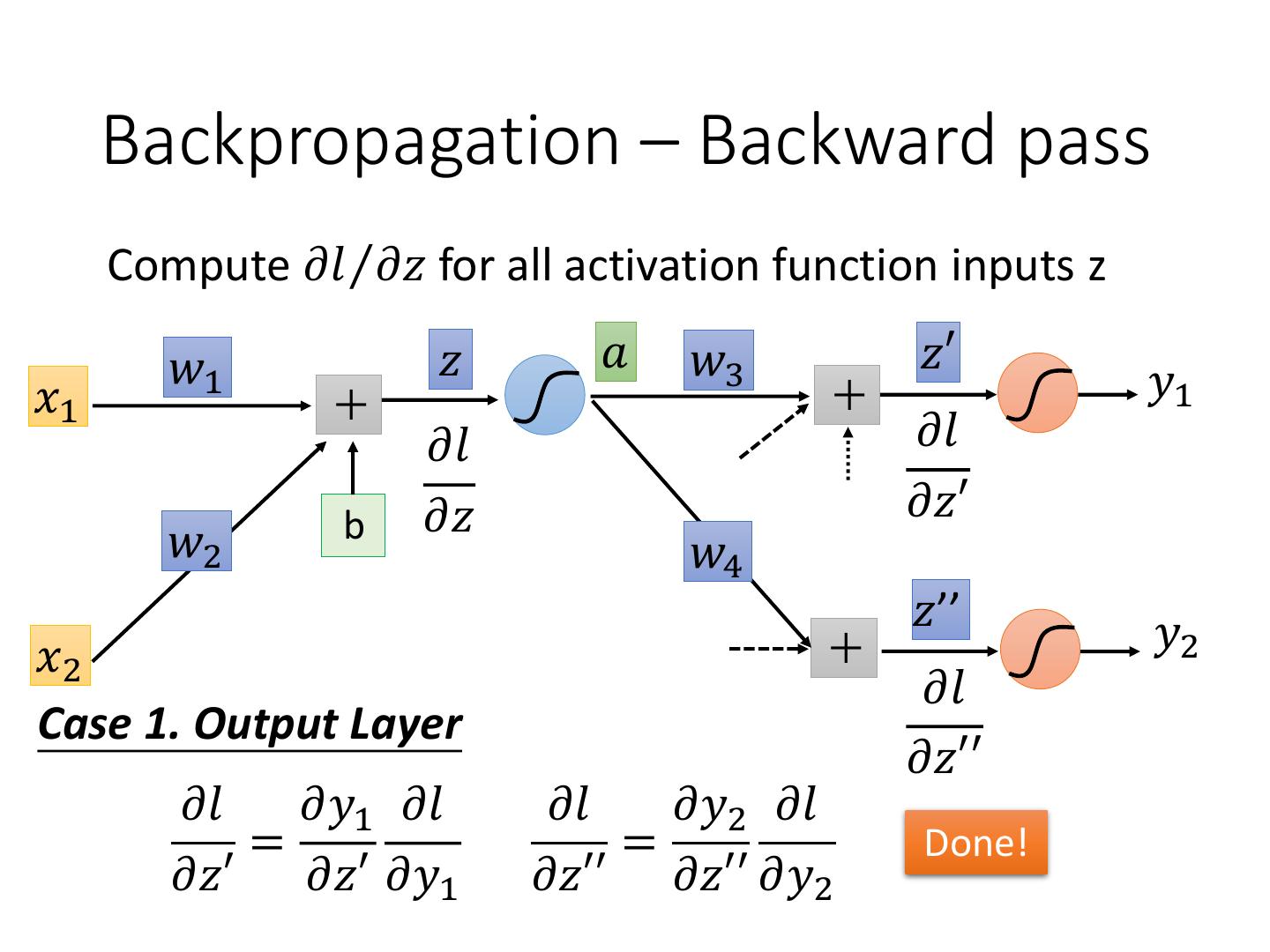
12 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z 𝑤1 𝑧 𝑎 𝑤3 𝑧′ 𝑥1 𝑦1 𝜕𝑙 𝜕𝑙 b 𝜕𝑧 𝜕𝑧′ 𝑤2 𝑤4 𝑧’’ 𝑦2 𝑥2 𝜕𝑙 Case 1. Output Layer 𝜕𝑧′′ 𝜕𝑙 𝜕𝑦1 𝜕𝑙 𝜕𝑙 𝜕𝑦2 𝜕𝑙 = = Done! 𝜕𝑧′ 𝜕𝑧′ 𝜕𝑦1 𝜕𝑧′′ 𝜕𝑧′′ 𝜕𝑦2
13 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z Case 2. Not Output Layer 𝑧′ …… 𝜕𝑙 𝜕𝑧′ 𝑧’’ …… 𝜕𝑙 𝜕𝑧′′
14 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z Case 2. Not Output Layer 𝑧′ 𝑎′ 𝑤5 𝑧𝑎 𝜕𝑙 𝜕𝑙 𝜕𝑧′ 𝜕𝑧𝑎 𝑤6 𝑧’’ 𝑧𝑏 𝜕𝑙 𝜕𝑙 𝜕𝑧′′ 𝜕𝑧𝑏
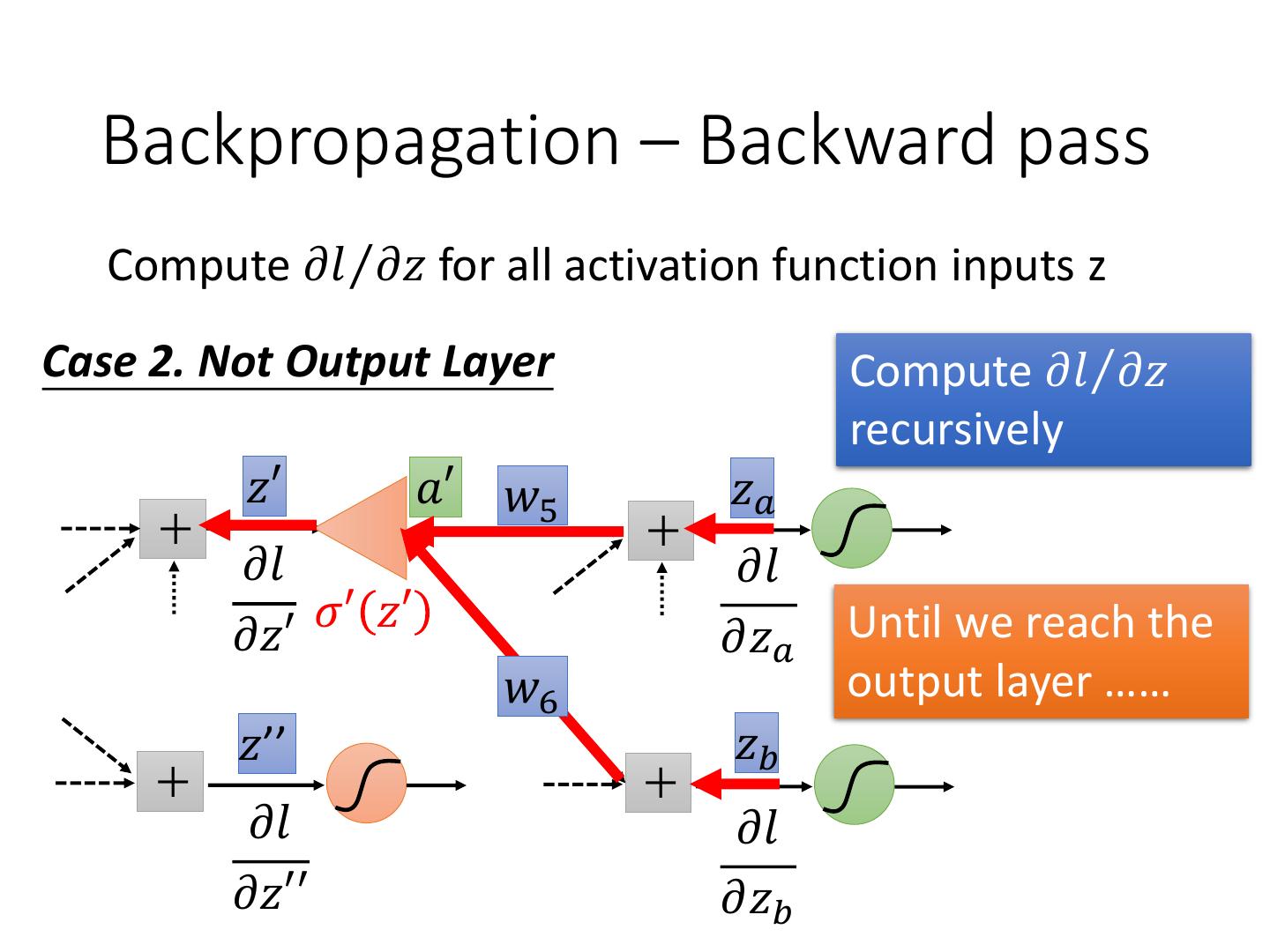
15 . Backpropagation – Backward pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z Case 2. Not Output Layer Compute 𝜕𝑙 Τ𝜕𝑧 recursively 𝑧′ 𝑎′ 𝑤5 𝑧𝑎 𝜕𝑙 𝜕𝑙 𝜕𝑧′ 𝜎′ 𝑧′ Until we reach the 𝜕𝑧𝑎 𝑤6 output layer …… 𝑧’’ 𝑧𝑏 𝜕𝑙 𝜕𝑙 𝜕𝑧′′ 𝜕𝑧𝑏
16 .Backpropagation – Backward Pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z Compute 𝜕𝑙 Τ𝜕𝑧 from the output layer 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑧1 𝜕𝑧3 𝜕𝑧5 𝑧1 𝑧3 𝑧5 𝑥1 𝑦1 𝑥2 𝑦2 𝑧2 𝑧4 𝑧6 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑧2 𝜕𝑧4 𝜕𝑧6
17 .Backpropagation – Backward Pass Compute 𝜕𝑙 Τ𝜕𝑧 for all activation function inputs z Compute 𝜕𝑙 Τ𝜕𝑧 from the output layer 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑧1 𝜕𝑧3 𝜕𝑧5 𝑧1 𝑧3 𝑧5 𝑥1 𝑦1 𝜎′ 𝑧1 𝜎′ 𝑧3 𝜎′ 𝑧2 𝜎′ 𝑧4 𝑥2 𝑦2 𝑧2 𝑧4 𝑧6 𝜕𝑙 𝜕𝑙 𝜕𝑙 𝜕𝑧2 𝜕𝑧4 𝜕𝑧6
18 .Backpropagation – Summary Forward Pass Backward Pass … … … 𝑎 … 𝜕𝑧 𝜕𝑙 𝜕𝑙 =𝑎 X = 𝜕𝑤 𝜕𝑧 𝜕𝑤 for all w