展开查看详情
1 .1 第七章 非线性方程 ( 组 ) 数值解法 —— 二分法 —— 不动点迭代及其加速
2 .2 内容提要 非线性方程求解基本概念 二分法 不动点迭代法及其加速 牛顿法、弦截法、抛物线法 求根问题的敏感性与多项式的零点 非线性方程组的数值求解
4 .4 基本概念 若 f ( x ) 是一次多项式，则称为 线性方程 ； 否则称为 非线性方程 f ( x ) = 0 代数方程： n =1, 2, 3, 4 时有相应的求根公式， n 5 时不存在求根公式 非线性方程可能有 ( 无穷 ) 多个解，一般要强调 求解区间 非线性方程一般没有直接解法，通常 用迭代法求数值解
5 .5 基本概念 实根 与 复根 根的 重数 ：若 且 , 则 为 的 重根 有根区间 ： 上至少存在 的一个实根 研究内容：在 有根 的前提下求出方程的 近似根
6 .6 二分法（对分法） 基本思想、数学原理、计算过程 收敛性分析
7 .7 二分法（对分法） 基本思想 将 有根区间 对分，并找出根所在的小区间，然后再对该小区间对分，依次类推，直到有根区间的长度足够小为止。 数学原理： 介值定理 设 在 上连续，且 ，则由介值定理可得，在 内至少存在一点 使得 适用范围 求有根区间内的 单重实根 或 奇重实根，即 用二分法求根，通常先给出 草图以确定有根区间
8 .8 二分法（对分法） x 1 x 2 x 3
9 .9 二分法 算法 ： (二分法 ) (1) 计算 f ( a ) ， f ( b ) ，若 f ( a ) f ( b ) >0 ，则算法失效，停止计算 (2) 令 ，计算 f ( x ) (3) 若 | f ( x )|< 或 | b-a |< ，停止计算，输出近似解 x (4) 若 f ( a ) · f ( x ) < 0 ，则令 b = x ; 否则令 a = x 优点： 简单易用，总是收敛 缺点： 收敛慢，不能求复根和偶数重根，一次只能求一个根 总结： 一般用来计算解的一个粗糙估计 (5) 返回第 2 步
10 .10 误差分析 记 a 1 = a , b 1 = b, 第 k 步的有根区间为 [ a k , b k ] 结论： 二分法总是收敛的！ ( 条件：函数满足介值定理 )
11 .11 不动点迭代 基本思想 迭代格式 收敛性分析（全局收敛与局部收敛）
12 .12 不动点迭代基本思想 构造 f ( x ) = 0 的一个等价方程： ( x ) 的不动点 f ( x ) = 0 x = ( x ) 等价变换 f ( x ) 的零点
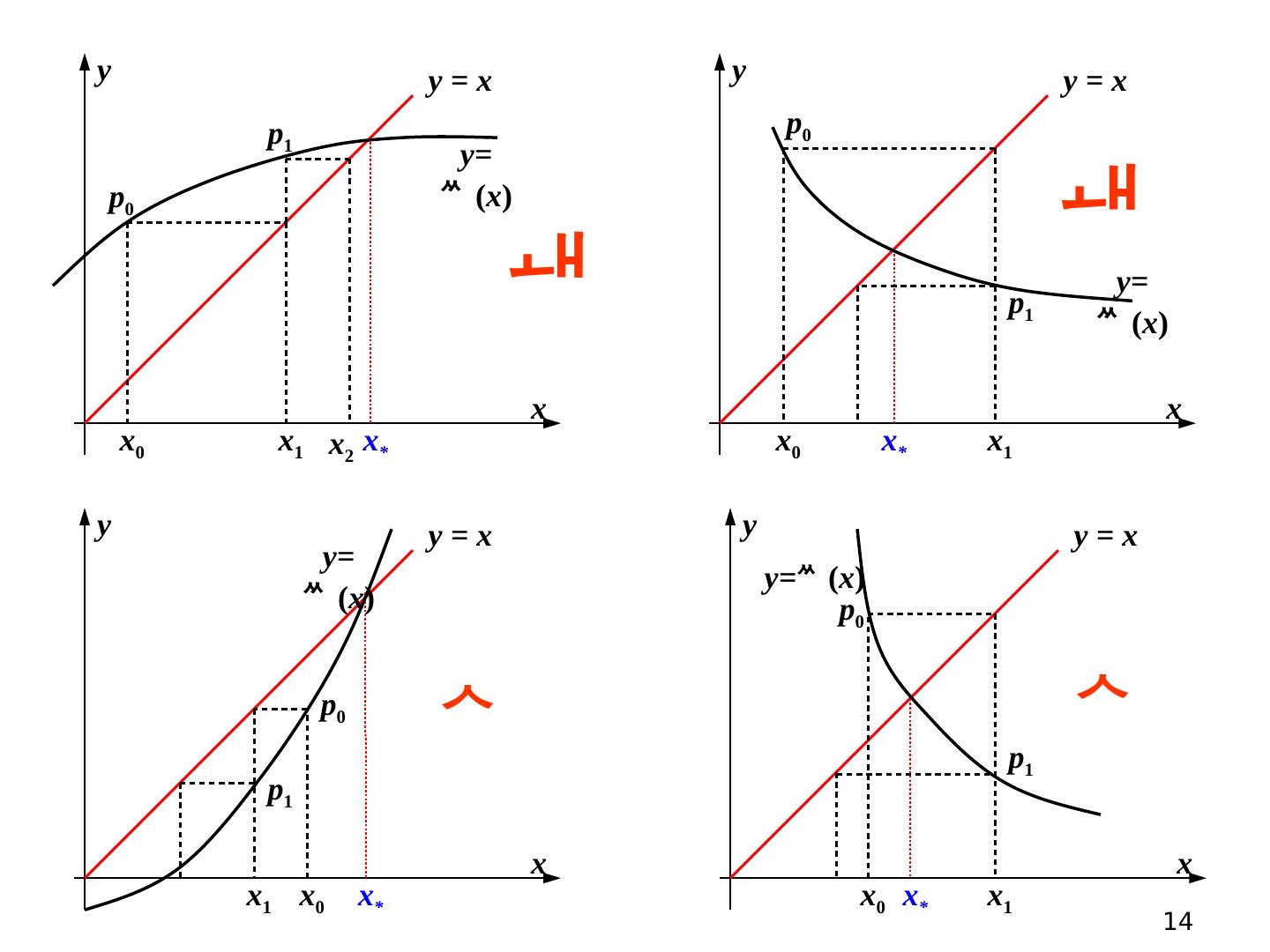
13 .13 不动点迭代格式 任取一个迭代初始值 x 0 ，计算 得到一个迭代序列： x 0 ， x 1 ， x 2 ， . . . ， x n ， . . . k = 0, 1, 2, ... ... 几何含义： 求曲线 y = ( x ) 与直线 y = x 的交点。
14 .14 x y y = x x y y = x x y y = x x y y = x x * x * x * x * y= ( x ) y= ( x ) y= ( x ) y= ( x ) x 0 p 0 x 1 p 1 x 0 p 0 x 1 p 1 x 0 p 0 x 1 p 1 x 0 p 0 x 1 p 1 x 2
15 .15 收敛性分析 设 ( x ) 连续，若 收敛，即 ，则 即 性质： 若 ，则不动点迭代 收敛 ，且 x * 就是 f ( x )=0 的解；否则迭代法 发散 。
16 .16 解的存在唯一性 定理 ： 设 ( x ) C [ a , b ] 且满足 对任意的 x [ a , b ] 有 ( x ) [ a , b ] 存在常数 0< L <1 ，使得任意的 x, y [ a , b ] 有 则 ( x ) 在 [ a , b ] 上存在 唯一的不动点 x * 证明：板书
17 .17 不动点迭代的收敛性判断 定理 ： 设 ( x ) C [ a , b ] 且满足 对任意的 x [ a , b ] 有 ( x ) [ a , b ] 存在常数 0< L <1 ，使得任意的 x, y [ a , b ] 有 则对任意初始值 x 0 [ a , b ] ，不动点迭代 x k +1 = ( x k ) 收敛，且 证明：板书 注： 一般来说， L 越小，收敛越快！
18 .18 不动点迭代的收敛性判断 推论： 若 ，对 任意 有 且对任意 有 则上述定理中的结论成立。 以上两个结论中的 收敛性与初始值的选取无关！ 全局收敛
19 .19 举例 例： 求 f ( x ) = x 3 – x – 1=0 在区间 [1, 2] 中的根 (1) (2) ex71.m 全局收敛
20 .20 不动点迭代的局部收敛 定义 ： 设 x * 是 ( x ) 的不动点，若存 在 x * 的某个 - 邻域 U ( x * ) =[ x * - , x * + ] ，对任意 x 0 U ( x * ) ，不动点迭代 x k +1 = ( x k ) 产生的点列都收敛到 x * ，则称该迭代 局部收敛 。 定理： 设 x * 是 ( x ) 的不动点，若 ’ ( x ) 在 x * 的某个邻域内连续，且 | ’ ( x * )| < 1 则 不动点迭代 x k +1 = ( x k ) 局部收敛 证明：板书
21 .21 收敛速度 定义： 设迭代 x k +1 = ( x k ) 收敛到 ( x ) 的不动点 x * ， 记 e k = x k x * ， 若 其中常数 C > 0 ，则称该迭代为 p 阶收敛 。 当 p =1 且 0< C < 1 时称为 线性收敛 当 p =2 时称为 二次收敛 ，或 平方收敛 当 p >1 或 p =1 且 C =0 时称为 超线性收敛 若 0<| ’ ( x * )|<1 ，则 不动点迭代 x k +1 = ( x k ) 局部线性收敛
22 .22 基本收敛定理 定理： 设 x * 是 ( x ) 的不动点 ， 若 ( p ) ( x ) 在 x * 的某邻域内连续，且 则迭代 x k +1 = ( x k ) 是 p 阶 局部收敛 的。且有 证明：板书
23 .22 基本收敛定理 定理： 设 x * 是 ( x ) 的不动点 ， 若 ( p ) ( x ) 在 x * 的某邻域内连续，且 则迭代 x k +1 = ( x k ) 是 p 阶 局部收敛 的。且有 证明：板书
24 .24 不动点迭代的加速 Aitken 加速技巧 Steffensen 迭代方法
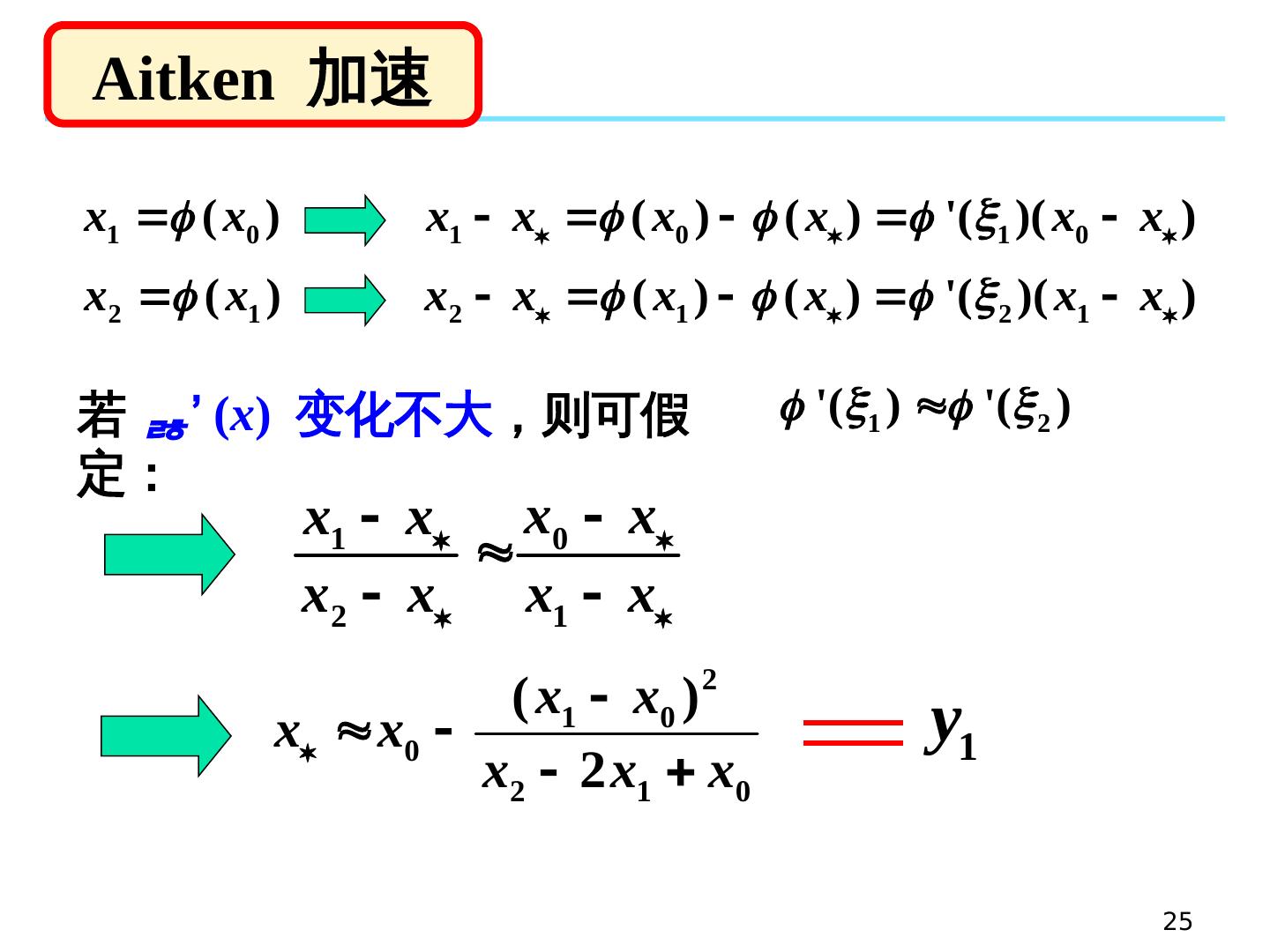
25 .25 Aitken 加速 若 ’ ( x ) 变化不大 ，则可假定： Aitken 加速
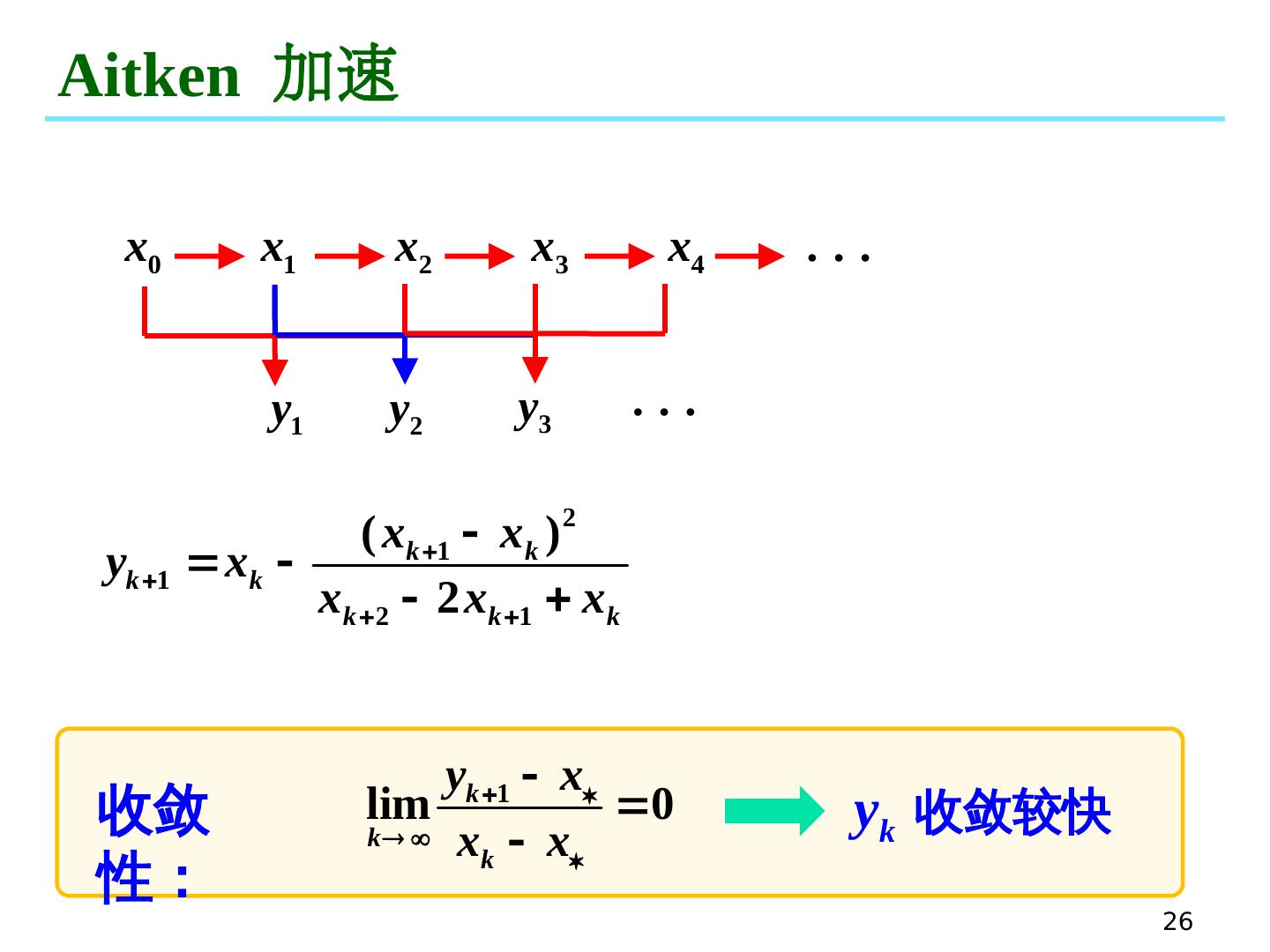
26 .26 Aitken 加速 收敛性： y k 收敛较快
27 .27 Steffenson 加速 基本思想： 将 Aitken 加速技巧与不动点迭代相结合 k = 0, 1, 2, . . . Steffensen 迭代函数： Steffensen 迭代
28 .28 Steffensen 迭代 定理： 若 是 的不动点 ， 则 是 的不动点。反之，若 是 的不动点，且 存在， ，则 是 的不动点。 另外，若原不动点迭代是线性收敛的，则 Steffensen 迭代是二阶收敛的。 若原迭代是 阶收敛的，则 Steffensen 迭代 阶收敛 原来不收敛的迭代， Steffensen 加速可能收敛 证明：略
29 .29 举例 例： 用 Steffensen 迭代法求 在区间 中的根（取 ） 例： 用 Steffensen 迭代法求 在区间 中的根（取 ） ex73.m ex74.m
热门城市
