- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
07-Newton 迭代法-弦截法、抛物线法
展开查看详情
1 .1 第七章 非线性方程 ( 组 ) 数值解法 —— Newton 迭代法 —— 弦截法、抛物线法
2 .2 本讲内容 Newton 法及其收敛性 简化的 Newton 法 Newton 下山法 弦截法与抛物线法
3 .3 基本思想、几何意义 二阶局部收敛性 简化 Newton 法 Newton 下山法 重根情形 Newton 迭代法
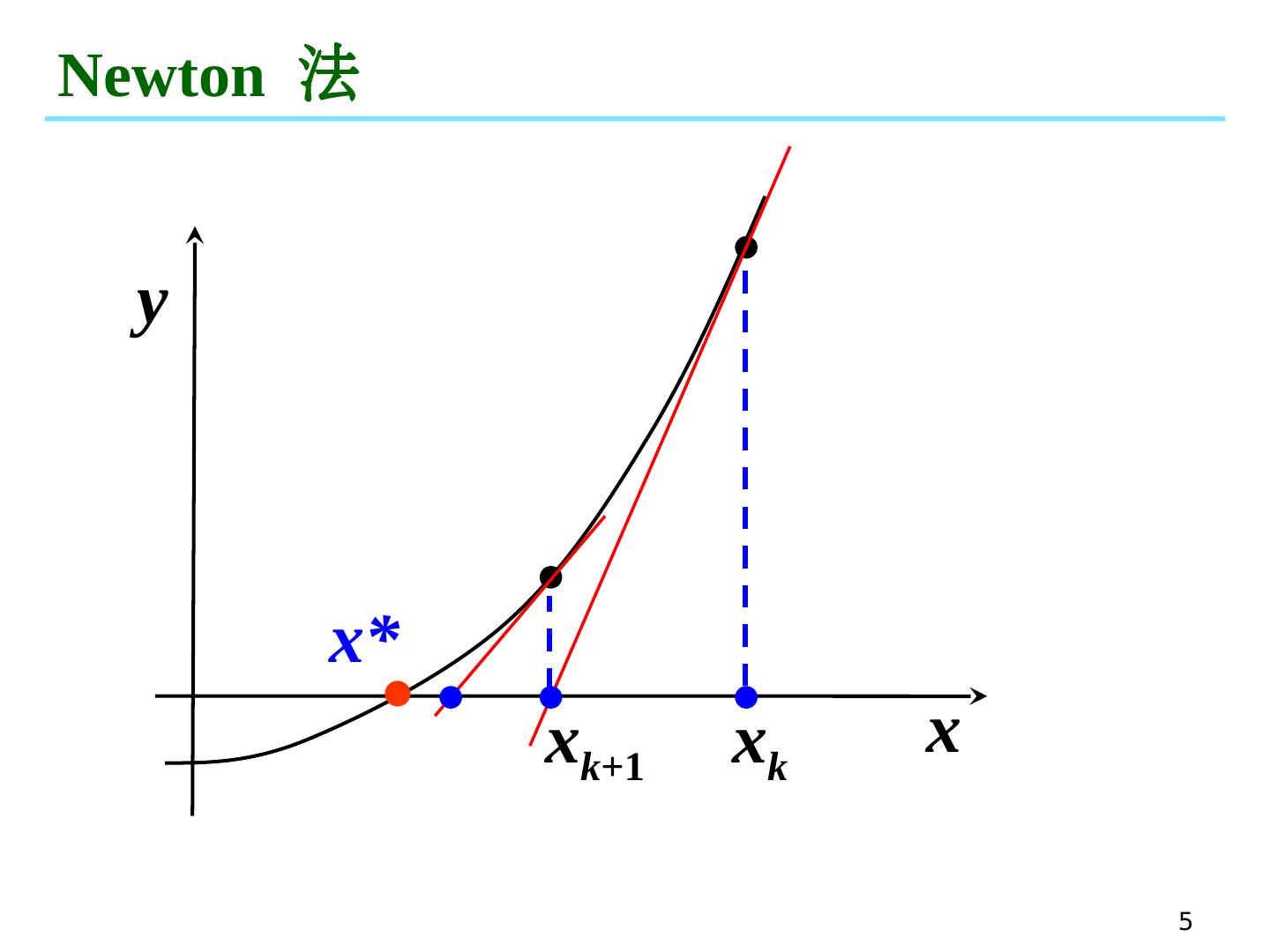
4 .4 Newton 迭代法 基本思想 将非线性方程 线性化 设 x k 是 f ( x )=0 的近似根,将 f ( x ) 在 x k 处 Taylor 展开 令: 条件: f ’ ( x ) 0
5 .5 Newton 法 x y x* x k x k +1
6 .6 Newton 法 算法 : ( Newton 法 ) (1) 任取迭代初始值 x 0 (2) 计算 (3) 判断收敛性:如果 或者 , 则算法收敛,停止计算,输出近似解 x 1 (4) 令 ,返回第二步
7 .7 收敛性 k = 0, 1, 2, . . . 迭代函数 牛顿法至少二阶 局部收敛
8 .8 举例 例: 用 Newton 法求 f ( x ) = x e x – 1=0 的解 ex75.m
9 .9 应用举例:计算平方根 例: 用 Newton 法求 f ( x ) = x 2 – C=0 的正根 解: 对任意 x 0 >0 ,总有 | q |<1 ,即牛顿法收敛
10 .10 牛顿 法 牛顿 的 优点 牛顿 法是目前求解非线性方程 ( 组 ) 的主要方法 至少二阶局部收敛,收敛速度较快,特别是当迭代点充分靠近精确解时。 牛顿 的缺点 对重根收敛速度较慢(线性收敛) 对初值的选取很敏感,要求 初值相当接近真解 先用其它算法获取一个近似解,然后使用牛顿法 每一次迭代都需要计算导数!
11 .11 简化的 Newton 法 线性收敛 基本思想: 用 f ’ ( x 0 ) 替代所有的 f ’ ( x k ) 好处: 只需要计算一次导数,即 f ’ ( x 0 ) 缺点: 只有线性收敛速度(假定方法是收敛的)
12 .12 Newton 下山法 下山因子的取法: 从 =1 开始,逐次减半,直到满足下降条件为止 基本思想: 要求每一步迭代满足下降条件 具体做法: 加 下山因子 保证全局收敛
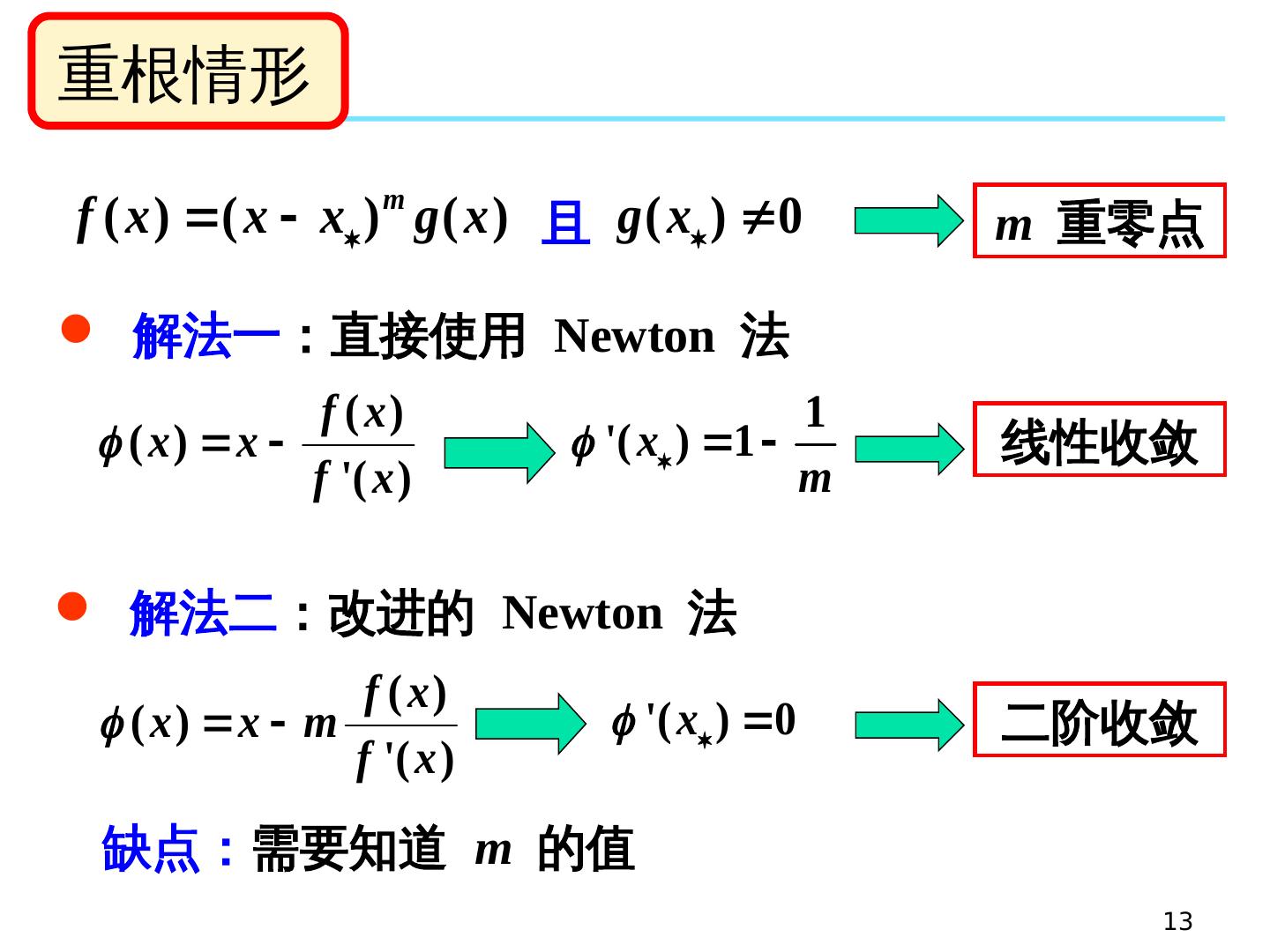
13 .13 重根情形 且 解法一 :直接使用 Newton 法 线性收敛 解法二 :改进的 Newton 法 二阶收敛 缺点: 需要知道 m 的值 m 重零点
14 .14 重根情形 x * 是 ( x )=0 的 单重根 解法三 :用 Newton 法解 ( x ) = 0 ,其中 迭代格式: 二阶收敛
15 .15 举例 例: 求 x 4 - 4 x 2 + 4=0 的二重根 (1) 普通 Newton 法 ex76.m (2) 改进的 Newton 法 (3) 用 Newton 法解 ( x ) = 0
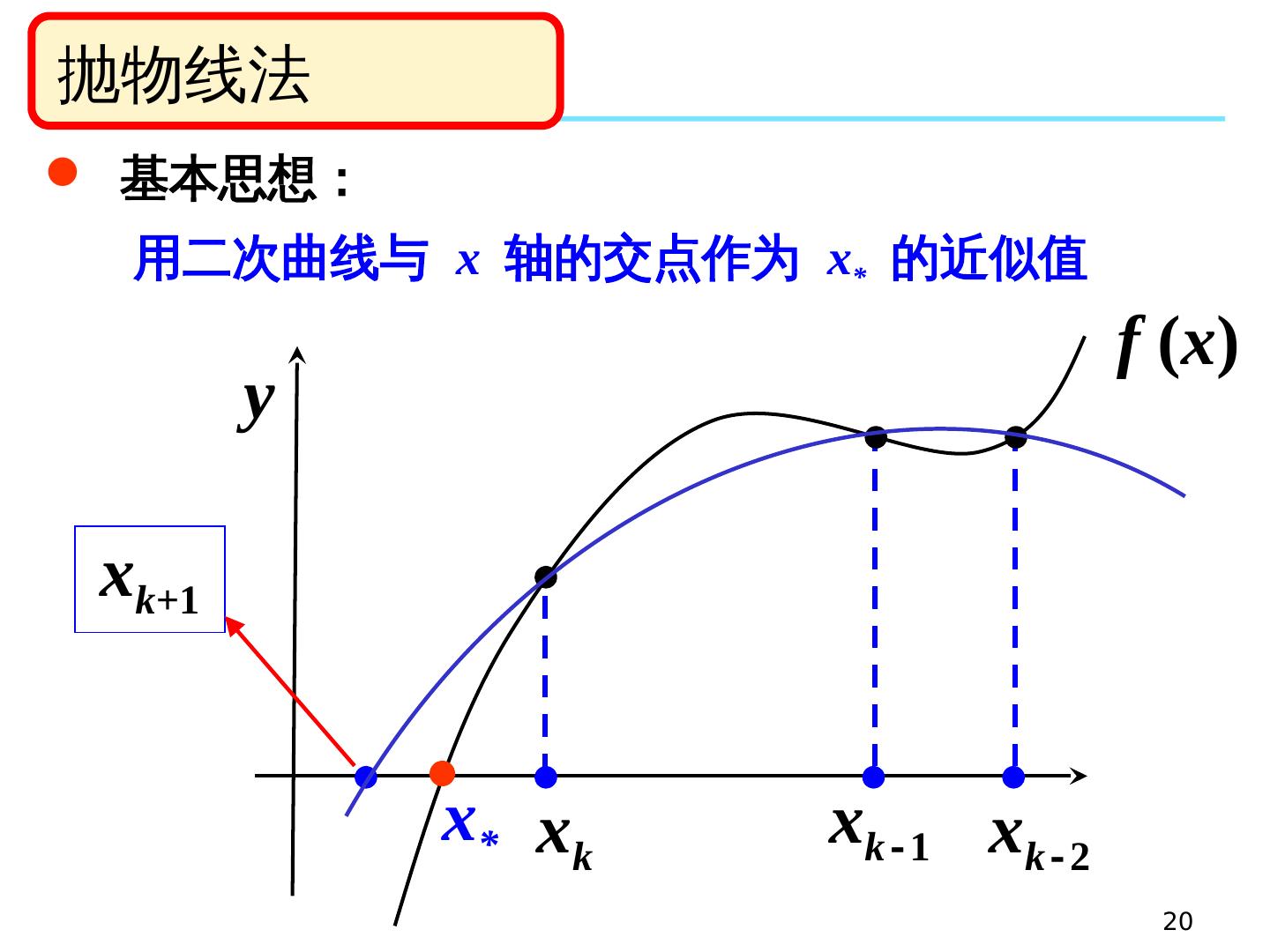
16 .16 弦截法与抛物线法 目的 :避免计算 Newton 法中的导数,并且尽可能地保持较高的收敛性(超线性收敛) 弦截法(割线法): 用差商代替微商 抛物线法: 用二次多项式近似 f ( x )
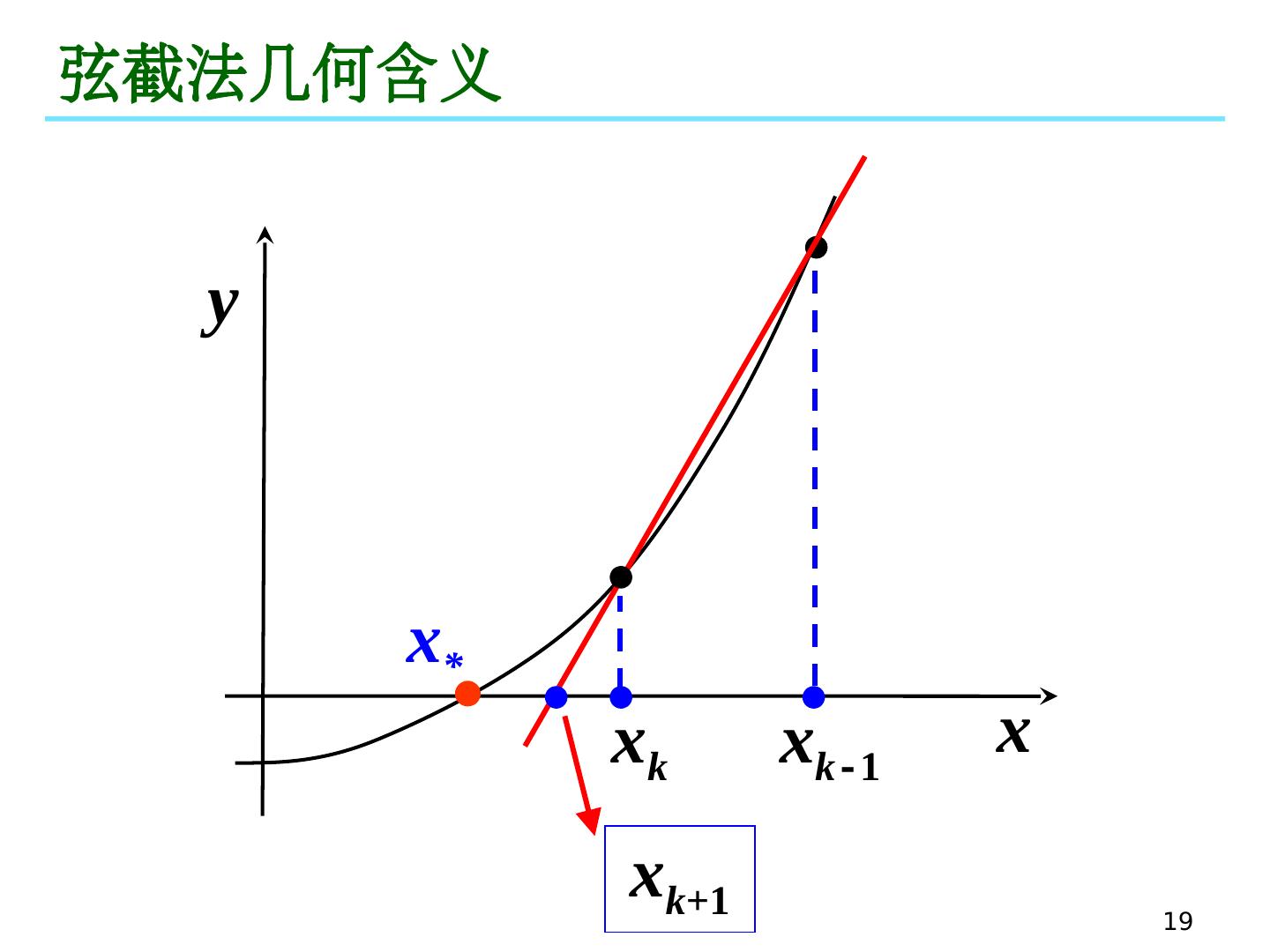
17 .17 弦截法 弦截法迭代格式: k = 1, 2, 3, . . . 注:弦截法需要提供 两个迭代初始值
18 .18 收敛性 定理: 设 x * 是 f ( x ) 的零点 , f ( x ) 在 x * 的某邻域 U ( x * , ) 内有二阶连续导数,且 f ’ ( x ) 0 ,若初值 x 0 , x 1 U ( x * , ) , 则当 充分小时,弦截法具有 p 阶收敛性,其中
19 .19 弦截法几何含义 x y x * x k - 1 x k x k +1
20 .20 抛物线法 基本思想: 用二次曲线与 x 轴的交点作为 x * 的近似值 y x k - 2 x k - 1 x k x k +1 f ( x ) x *
21 .21 抛物线法 计算过程 二次曲线方程 ( 三点 Newton 插值多项式 ) 问题: p 2 ( x ) 与 x 轴有 两个交点 ,取哪个点? 解决方法: 取靠近 x k 的那个点 !
22 .22 抛物线法 取靠近 x k 的那个点 抛物线法可能涉及复数运算,有时可以用来求复根
23 .23 收敛性 在一定条件下可以证明:抛物线法的收敛阶为 与弦截法相比,抛物线法具有更高的收敛阶 抛物线法需提供三个初始值 抛物线法也称为 Muller 法
24 .24 作业 1. 教材第 239 页: 10 , 12 , 15 提示: 第 10 题假定 x 是 单重根,并假定迭代收敛 第 12 题设 a 0 ,讨论全局收敛性,即对任意 x 0 ,收敛性如何? 第 15 题加条件: a 0