- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
06-线性方程组的迭代法--共轭梯度法(CG)
展开查看详情
1 .第六章 线性方程组的迭代法 — 共轭梯度法 ( CG )
2 .2 线性方程组与极值问题 最速下降法 CG 方法(共轭梯度法) CG 方法
3 .2 线性方程组与极值问题 最速下降法 CG 方法(共轭梯度法) CG 方法
4 .4 梯度下降法 基本思想: 选取 一 个初始向量 x (0) (2) 确定一个下降方向 p (0) ,从 x (0) 出发,沿方向 p (0) 找极小点 x (1) (3) 以 x (1 ) 点为新的出发点,确定一个新的下降方向 p (1) ,从 x (1) 出发 , 沿 p (1) 找极小点 x (2) (4) 以此类推,不断寻找新的点 x ( k ) ,直到找出最小值点 x 求解线性方程组 Ax = b 求 ( x ) 的最小值点 ( 极小值点 )
5 .5 两个基本问题 问题一 :如何确定 下降方向 ? 问题二 :如何确定 步长 ?
6 .6 最速下降法 基本思想: 任取一个迭代初始向量 x (0) ,构造迭代序列 x (0) , x (1) , x (2 ) , . . . , 使得 ( x (0) ) > ( x (1) ) > ( x (2) ) > . . . ,且每一步都 以 最快 的 速度 下降 到 ( x ) 的极小值。 具体作法: 设 x ( k ) 已经求得,计算 x ( k +1) : ( x ) 沿 x ( k ) 处的 最速下降 方向,即 负梯度方向 r ( k ) = -( Ax ( k ) - b ) 的 最小值点,即
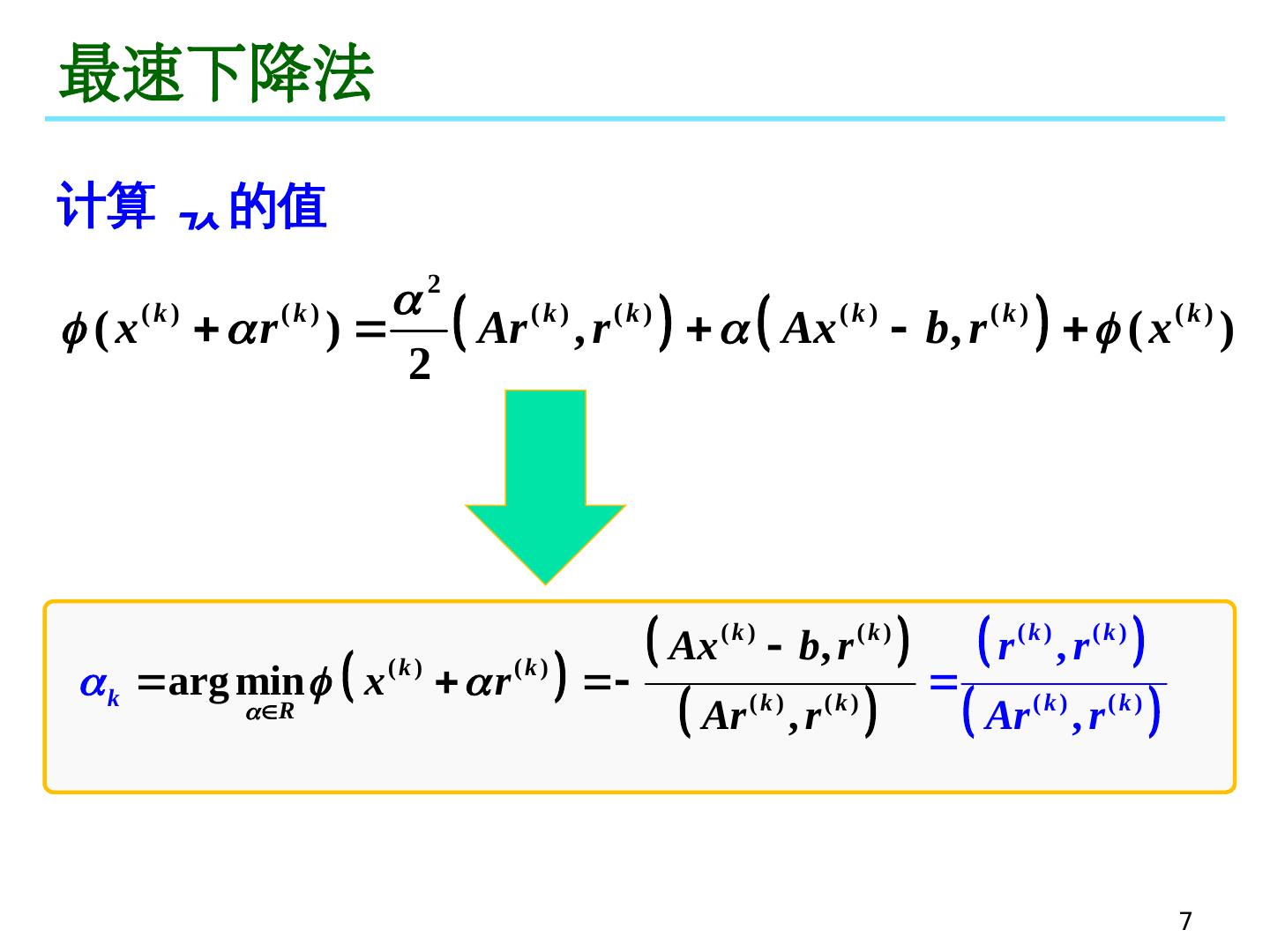
7 .7 最速下降法 计算 的值
8 .8 最速下降法 算法 : (最速下降法) (3) 对 k = 0, 1, 2, ... , 计算 若 ,则输出 x x ( k +1) ,停止 计算。 给定初值 x (0 ) 和精度要求 计算
9 .9 最速下降法的收敛性 定理 : 设 A 对称正定 ,其特征值为 则由最速下降法产生的序列满足 且有 缺点 : (1) 若 1 >> n ,则收敛很 慢,并可能出现不稳定现象 ( 舍入误差 ) (2) 每次的下降方向为 局部下降最快 ,并非全局最快
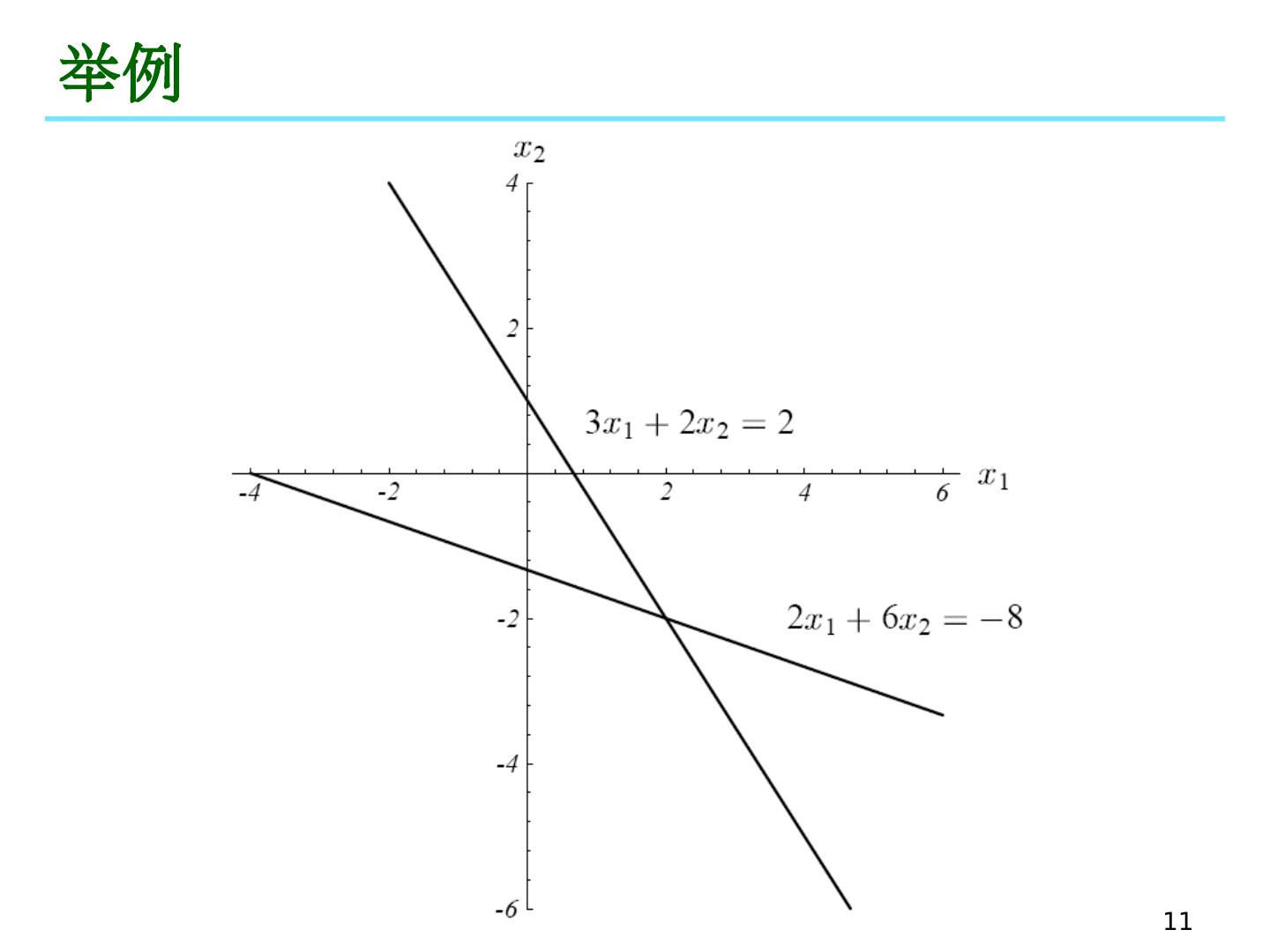
10 .10 举例
11 .11 举例
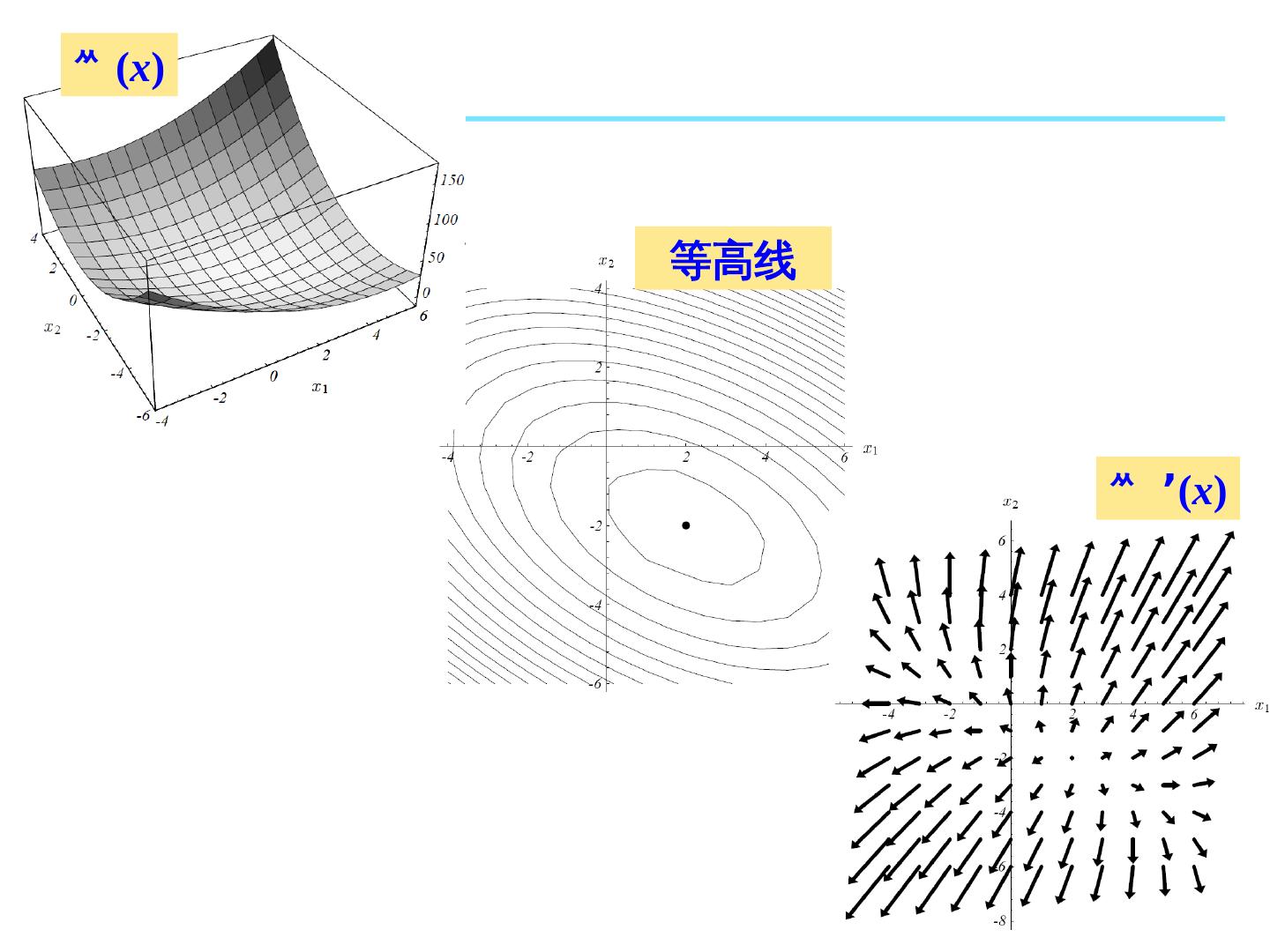
12 .12 举例 等高线 ’ ( x ) ( x )
13 .13 举例 最 速 下 降 法
14 .14 共轭梯度法 出发点 : 在确定 x ( k +1) 时,不沿负梯度方向取极小,而是寻找一个更好的方向 p ( k ) ,使得 ( x ) 下降得更快! 定义 : 设 A 对称正定 ,若 ( x , Ay ) =0 ,则称 x , y 关于 A 正交 ( A- 正交 ) 或 A - 共轭 ,若 z 1 , z 2 , . . . , z n 相互 A - 共轭,则称 z 1 , z 2 , . . . , z n 构成 A - 正交向量组或 A - 共轭向量 组 。
15 .15 共轭梯度法 具体作法 : 令 p (0) = r (0) ,设 x ( k ) 已经求得,则 x ( k +1) 由下面的公式确定: 其中
16 .16 共轭梯度法 定理: 设 A 对称正定 ,则由 CG 算法产生的序列满足 (1) 当 i j 时, ( r ( i ) , r ( j ) ) =0 ,即 r (0) , r (1) , r (2) , . . . 相互正交 (2) 当 i j 时, ( p ( i ) , Ap ( j ) ) =0 ,即 p (0) , p (1) , p (2) , . . . 相互 A- 共轭 证明 :略 参数的新计算公式:
17 .17 共轭梯度法 算法 : (共轭梯度法) (3) 对 k = 0, 1, 2, ... , 计算 给定初值 x (0 ) 和精度要求 计算 ,令 若 ,则输出 x = x ( k +1) ,停止 计算 。
18 .18 共轭梯度 法 的收敛性 定理 : 设 A 对称正定 ,则共轭梯度法至多 n 步就能找到精确解。 定理 : 设 A 对称正定 , x 为精确解, x ( k ) 为共轭梯度法的数值解,则有 其中