06-线性方程组的迭代法--Jacobi, G-S and SOR

1 .1 第六章 线性方程组的迭代法 — Jacobi , G-S and SOR

2 .2 本讲内容 Jacobi 迭代法 Gauss-Seidel 迭代法 SOR （超松弛）迭代法 迭代法收敛性分析 几类基本迭代法

3 .3 Jacobi, G-S, SOR

4 .4 Jacobi 迭代 考虑线性方程组 Ax = b 其中 A =[ a ij ] n  n 非奇异，且对角线元素全不为 0 将 A 分裂成 A = D - L - U ， 其中 Jacobi 迭代法

5 .5 Jacobi 迭代 k = 0 , 1, 2, … 取 M = D ， N = L + U ，可得 雅可比 (Jacobi) 迭代方法 迭代矩阵记为： 分量形式： i = 1, 2, … , n ， k = 0 , 1, 2, … Jacobi 迭代法

6 .6 Gauss-Seidel 迭代 在计算 时 ，如果用 代替 ， 则可能会得到更好的收敛效果。

7 .7 Gauss-Seidel 迭代 写成矩阵形式 : 此迭代方法称为 高斯 - 塞德尔 ( G auss - S eidel ) 迭代法 k = 0 , 1, 2, … 可得 迭代矩阵记为： Gauss-Seidel 迭代

8 .8 SOR 迭代 为了得到更好的收敛效果，可在修正项前乘以一个 松弛因子  ，于是可得迭代格式 G-S 迭代法的分量形式

9 .9 SOR 迭代 写成矩阵形式 : 可得 —— SOR ( S uccessive O ver- R elaxation ) 迭代方法 迭代矩阵记为： SOR 的优点 ： 通过选取合适的  ，可获得更快的收敛速度 SOR 的缺点 ： 最优参数  的 选取比较困难 SOR 迭代

10 .10 Jacobi 、 G-S 、 SOR Jacobi 迭代 SOR 迭代 G-S 迭代

11 .11 举例 例 ： 分别用 Jacobi 、 G-S 、 SOR (  = 1.1 ) 迭代解线性方程组 取初始向量 x (0) = [0 , 0, 0] T ， 迭代过程中小数点后保留 4 位。 解： Jacobi 迭代： 计算可 得： x (1) = [ 0.5000, 2.6667, -2.5000 ] T x (21) = [ 2.0000, 3.0000, -1.0000 ] T

12 .12 举例 G-S 迭代： x (1) = [ 0.5000, 2.8333, -1.0833 ] T x (9) = [ 2.0000, 3.0000, -1.0000 ] T 迭代可得：

13 .13 举例 SOR 迭代： 取  = 1.1 ，迭代可得 x (1) = [ 0.5500, 3.1350, -1.0257 ] T x (7) = [ 2.0000, 3.0000, -1.0000 ] T 如何确定 SOR 的 最优松弛因子是一 件 非常困难 的 事！

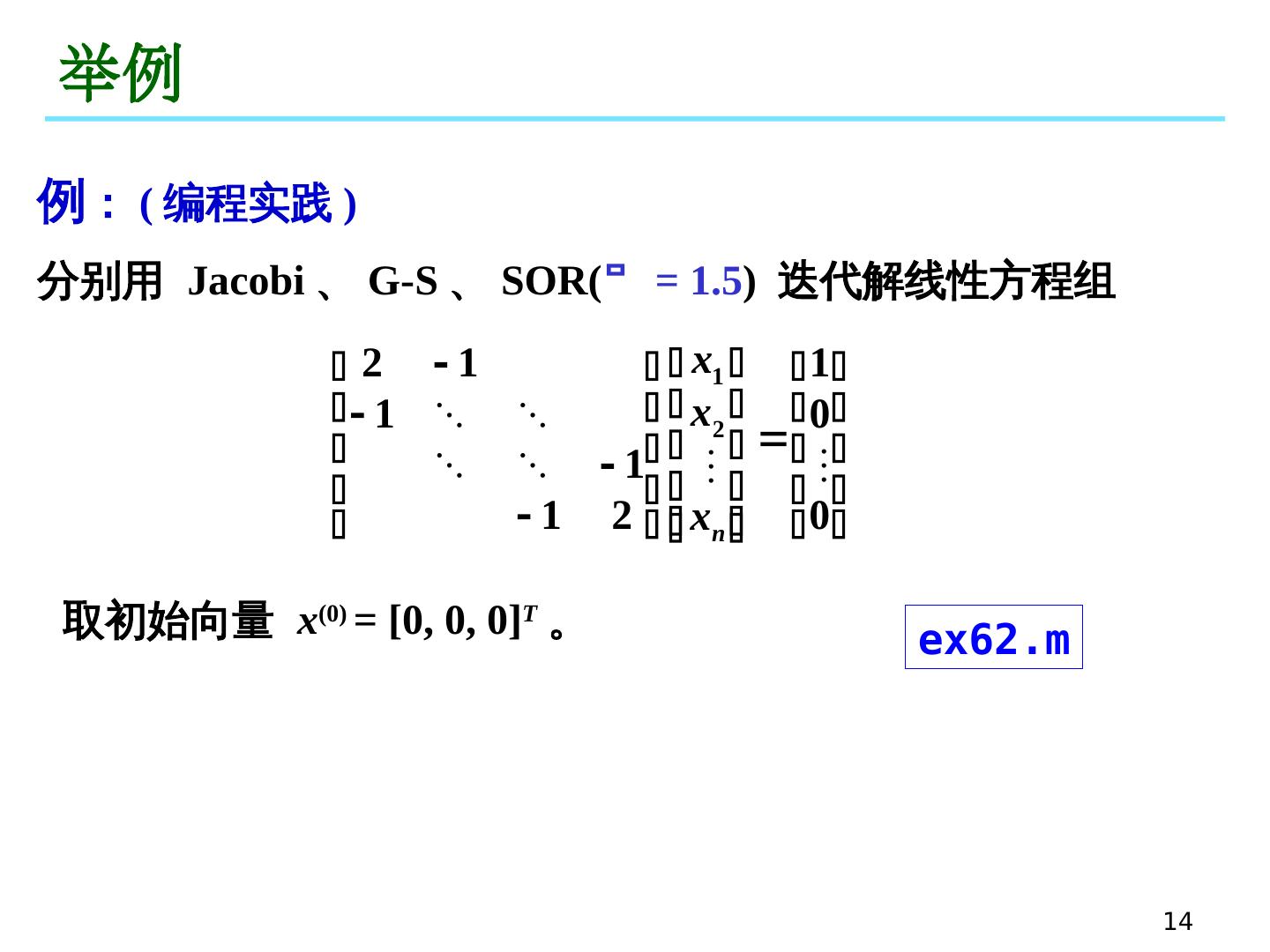
14 .14 举例 例 ： ( 编程实践 ) 分别 用 Jacobi 、 G-S 、 SOR(  = 1.5 ) 迭代解线性方程组 取初始向量 x (0) = [0 , 0, 0] T 。 ex62.m

15 .15 迭代方法的收敛性 Jacobi 迭代收敛的 充要 条件  ( J )<1 G-S 迭代收敛的 充要 条件  ( G )<1 SOR 迭代收敛的 充要 条件  ( L  )<1 Jacobi 迭代收敛的 充分 条件 || J|| <1 G-S 迭代收敛的 充分 条件 ||G || < 1 SOR 迭代收敛的 充分 条件 || L  || < 1 对角占优、不可约矩阵 对称正定矩阵

16 .16 对角占优矩阵 且 至少有一个 不等式严格成立，则称 A 为 弱对角占优 ； 若 所有不等式 都严格成立，则称 A 为 严格对角占优 。 ( i = 1, 2, ... , n ) 定义 ： 设 A R n  n ，若

17 .17 可 约矩阵与 不可 约矩阵 定义 ： 设 A R n  n ，若 存在置换矩阵 P 使得 则称 A 为 可约矩阵 ； 否则称为 不可约矩阵 。 如果 A 是可约矩阵，则方程组 Ax = b 等价于 y 即可以把原方程组化成两个 低阶 的方程组来处理。 f

18 .18 可约 矩阵的几个简单判别方法 性质： 设 A R n  n ， 若 A 的所有元素都非零，则 A 不可约。 性质： 设 A R n  n ，且 n 2 。 若 A 可约，则 A 的零元素个数大于等于 n -1 。 性质： 设 A R n  n 是 三对角矩阵，且三条对角线元素均非零，则 A 不可约。 思考： 如 A 是 三对角矩阵，上、下 次对角线 元素均非零，则 A 是不是不可约？

19 .19 Jacobi 、 G-S 收敛性 定理 ： 若 A 严格对角占优 或 不可约弱对角占优 ，则 A 非奇异 定理 ： 若 A 严格对角占优 或 不可约弱对角占优 ，则 Jacobi 迭代和 G-S 迭代均收敛 证明 ：仅证明严格对角占优情形 证明：板书 对角占优情形

20 .20 Jacobi 、 G-S 收敛性 定理 ： 设 A 对称且 D 正定，则 Jacobi 迭代收敛的 充要条件 是 A 和 2 D  A 都正定。 证明：略 定理 ： 设 A 对称且 D 正定，则 G-S 迭代收敛的 充要条件 是 A 正定。 证明：略 对称正定情形

21 .21 SOR 收敛性 定理 ： 若 SOR 迭代收敛，则 0 <  < 2 。 SOR 收敛的必要条件 定理 ： 若 A 对称正定，且 0 <  < 2 ， 则 SOR 迭代收敛。 SOR 收敛的充分条件 定理 ： 若 A 严格对角占优或不可约弱对角占优，且 0 <   1 ， 则 SOR 迭代收敛。 证明：板书 证明：板书 证明：略

22 .22 收敛性小结 A 严格对角占优或不可约弱对角占 优且 0 <   1 A 对称 正定，则 SOR 迭代 收敛 0 <  < 2 A 对称且对角线元素为正，则 Jacobi 迭代 收敛 A 正定 且 2 D - A 正定 G-S 迭代 收敛 A 正定 A 严格对角占优或不可约弱对角占 优 Jacobi 和 Gauss-Seidel 迭代收敛 SOR 迭代 收敛

23 .23 举例 例 ： 设 ，给出 Jacobi 和 G-S 收敛的充要条件 解： A 对称，且对角线元素均大于 0 ，故 (1) Jacobi 收敛的充要条件是 A 和 2D-A 均正定 (2) G-S 收敛的充要条件是 A 正定 A 正定 2 D - A 正定 Jacobi 收敛的充要条件是： -0.5< a <0.5 G-S 收敛的充要条件是： -0.5< a <1

24 .24 举例 解法二： Jacobi 的迭代矩阵为 设  是 J 的特征值，则由 det(  I - J ) = 0 可得 (  - a ) 2 (  +2 a ) = 0 Jacobi 收敛的充要条件是  ( J )<1  | |<1 ， 即 -0.5< a <0.5

25 .25 补：算法的实施 停机准则 ： 算法 ： Jacobi 给定初值 x (0 ) 和精度要求 tol 计算 (3) 对 k = 0, 1, 2, ... , 计算 若 ，则输出 x   x ( k +1) ，停止 计算。 ， i = 1, 2, ..., n （ G-S 和 SOR 的实施类似）

26 .26 作业 1. 教材第 209 页： 1(1) ， 2 ， 3 ， 4 2. 已知线性方程组如下，写出 Jacobi ， Gauss-Seidel 和 SOR （  =1.5 ） 方法的分量格式，并判断这三个 方法 的收敛性 注： 第 1 题 , 系数矩阵改为 第 2(1) 、 2(2) 题中 的 系数矩阵分别改为 和 第 4 题中 的系数矩阵分别改为