06-迭代法基本概念

1 .1 第六章 线性方程组的迭代解法 — 迭代法基本概念

2 .2 本章内容提要 迭代算法基本概念 Jacobi 迭代法和 Gauss-Seidel 迭代法 SOR （超松弛）迭代法 共轭梯度法

3 .3 本讲内容 向量序列与矩阵序列的极限 迭代法的构造 迭代法的收敛性判断 迭代法的基本概念

4 .4 向量序列的收敛 矩阵序列的收敛

5 .5 向量序列的极限 定义 ： 设向量序列 ， ， 若存在向量 ，使得 i = 1, 2, … , n 则称向量序列 收敛到 x ，记作 每个分量组成的序列都收敛 称 x 是向量序列 x ( k ) 的 极限

6 .6 矩阵序列的极限 定义 ： 设矩阵序列 ，若存在矩阵 ，使得 则称矩阵序列 { A k } 收敛到 A ，记作 i , j = 1, 2, … , n 例： 设 0 < | a| < 1 ，考察下面矩阵序列的极限

7 .7 矩阵极限判断 定理 ： 证明：只需证明无穷范数情形 ( 其中 || · || 为任一矩阵范数 ) 推论 ： 推论 ：

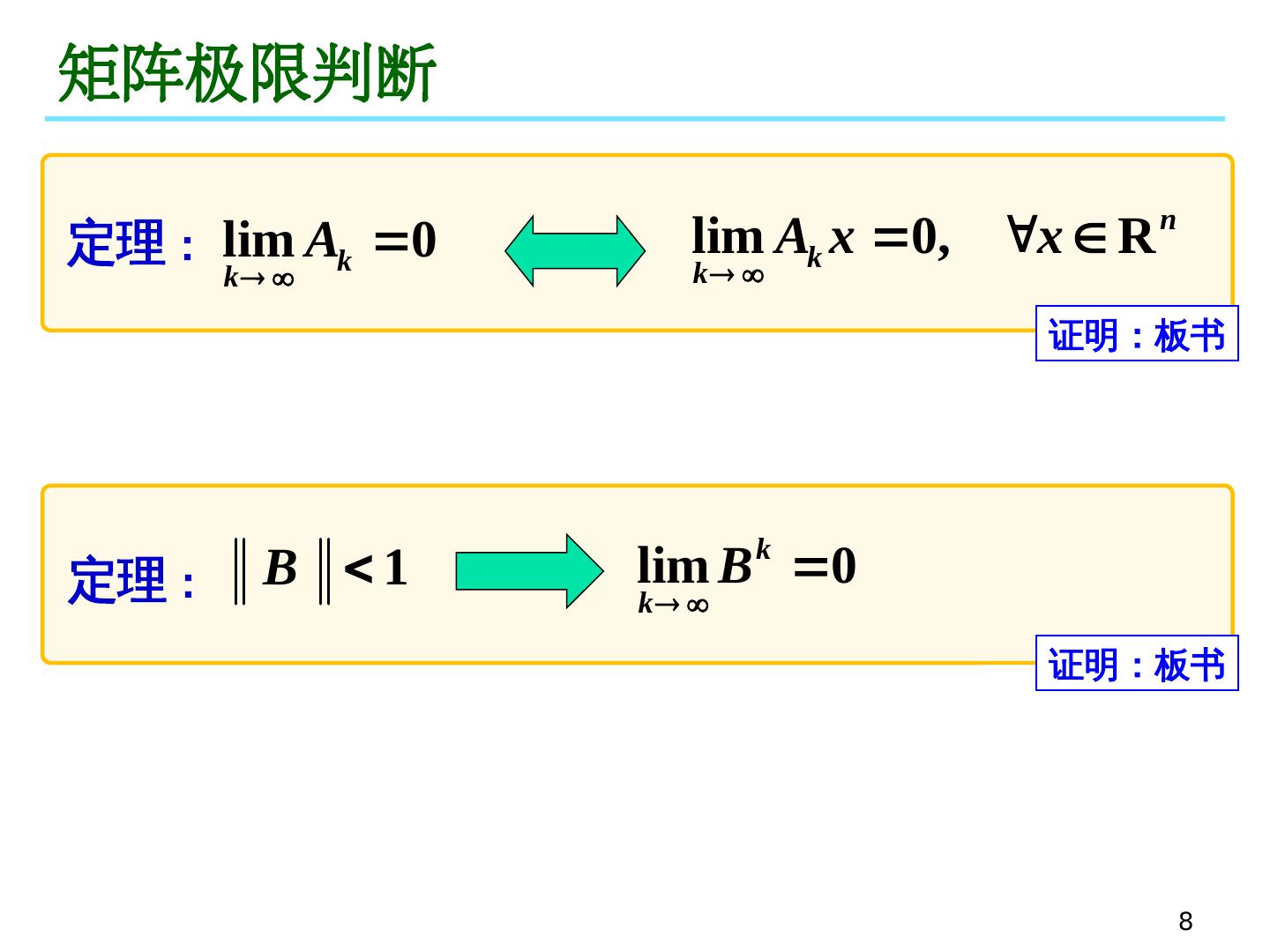
8 .8 矩阵极限判断 定理 ： 证明：板书 定理 ： 证明：板书

9 .9 矩阵极限判断 定理 ： 定理 ： ( 其中 || · || 为任一矩阵范数 ) 证明：板书 定理 ： 存在某算子范数 ，使得 自行证明 证明：板书

10 .10 线性方程组 迭代法

11 .11 线性方程组迭代法 运算量大，不适合大规模的线性方程组求解 无法充分利用系数矩阵的稀疏性 直接法的缺点 从一个初始向量出发，按照一定的迭代格式，构造出一个趋向于真解的向量序列。 只需存储系数矩阵中的非零元素 运算量不超过 O ( kn 2 ) ，其中 k 为迭代步数 迭代法是目前求解大规模线性方程组的主要方法 迭代法

12 .12 迭代法的构造 矩阵分裂迭代法基本思想 Ax = b k = 0 , 1, 2, … 给定一个初始向量 x (0) ，可得 迭代格式 其中 B = M -1 N 称为 迭代矩阵 A = M - N Mx = Nx + b M 非奇异 A 的一个 矩阵分裂

13 .13 矩阵分裂迭代法 k = 0 , 1, 2, … 定义 ： 若 存在，则称该迭代法 收敛 ，否则称为 发散 性质 ： 若 ，则 x * 为原方程组 Ax = b 的解 注：这里用 x * 表示真解，教材上用 x *

14 .14 迭代法的收敛性 定理 ： 对任意初始向量 x (0) ，上述迭代格式收敛的充要条件是 定理 ： 若存在算子范数使得 ||B|| < 1 ，则上述迭代格式收敛。 例 ： 考虑迭代法 x ( k +1) = Bx ( k ) + f 的收敛性，其中 证明：板书

15 .15 迭代法的收敛性 B = M -1 N 定理 ： 若存在算子范数 || · || ，使得 ||B|| = q <1 ，则 迭代法收敛 证明：板书

16 .16 收敛速度 第 k 步的误差： 平均每次迭代后的误差压缩率约为： 若要求 k 步迭代后上述误差比值不超过  ，则 迭代法的收敛速度

17 .17 收敛速度 定义 ： 迭代法 x ( k +1) = Bx ( k ) + f 的平均收敛速度定义为 渐进收敛速度为  ( B ) 越小，迭代收敛越快 迭代法的收敛速度

18 .18 作业 1. 教材第 210 页： 5 ， 9 注： 第 5 题中的系数矩阵改为