05-矩阵三角分解法

1 .1 第五章 线性方程组直接解法 — 矩阵三角分解法

2 .2 本讲内容 LU 分解与 PLU 分解 一般线性方程组 Cholesky 分解 －－ 平方根法 对称正定线性方程组 追赶法 对角占优三对角线性方程组

3 .3 LU 分解 将一个矩阵分解成结构简单的 三角矩阵的乘积 什么是矩阵的三角分解 矩阵的 LU 分解 矩阵的 LDR 分解 克洛脱 ( Crout ) 分解 Gauss 消去法对应的矩阵三角分解

4 .4 矩阵的 LU 分解 LU 分解 --- 待定系数法（ Doolittle 分解 ） 列主元 LU 分解

5 .5 LU 分解 利用矩阵乘法直接计算 LU 分解 —— 待定系数法 L  U = A  比较等式两边的 第一行 得： u 1 j = a 1 j 比较等式两边的 第一列 得：  比较等式两边的 第二行 得： 比较等式两边的 第二列 得： ( j = 1,…, n ) ( i = 2,…, n ) ( j = 2,…, n ) ( i = 3,…, n ) U 的第一行 L 的第一列 U 的第二行 L 的第二列

6 .6 计算 LU 分解 第 k 步：此时 U 的前 k -1 行和 L 的前 k -1 列已经求出 比较等式两边的 第 k 行 得： 比较等式两边的 第 k 列 得： 直到第 n 步，便可求出矩阵 L 和 U 的所有元素。 ( j = k , …, n ) ( i = k +1, …, n ) 这种计算 LU 分解的方法也称为 Doolittle 分解

7 .7 LU 分解 算法 ： ( LU 分解 ) for k = 1 to n end j = k , …, n i = k +1, …, n ex51.m 运算量： ( n 3 - n )/3 为了节省存储空间，通常用 A 的绝对下三角部分来存放 L ( 对角线元素无需存储)，用 A 的上三角部分来存放 U

8 .8 LU 分解算法 算法 ： ( LU 分解求解方程组 ) % 先计算 LU 分解 for k = 1 to n end % 解三角方程组 Ly = b 和 Ux = y

9 .9 PLU 分解 for k = 1 to n end i = k , k +1, …, n j = 1, 2, …, n i = k +1, …, n j = k +1, …, n 列主元 Gauss 消去法 —— PLU 分解 此算法可以用于计算矩阵的行列式和逆 Matlab 程序：上机练习

10 .10 PLU 分解算法 for k = 1 to n end % 解三角方程组 Ly = Pb 和 Ux = y 算法 ： ( P LU 分解求解方程组 )

11 .11 对称正定矩阵 Cholesky 分解 平方根法 改进的平方根法

12 .Cholesky 分解 对称正定矩阵的三角分解 —— Cholesky 分解 定理： ( Cholesky 分解 ) 若 A 对称正定，则 A 可唯一分解为 其中 L 为下三角矩阵，且对角元素都大于 0 A = LL T 证明 : 板书 定理： 设 A 是对称矩阵，若 A 的所有顺序主子式都不为 0 ，则 A 可唯一分解为 其中 L 为单位下三角阵， D 为对角矩阵 A = LDL T 证明 : 自行练习

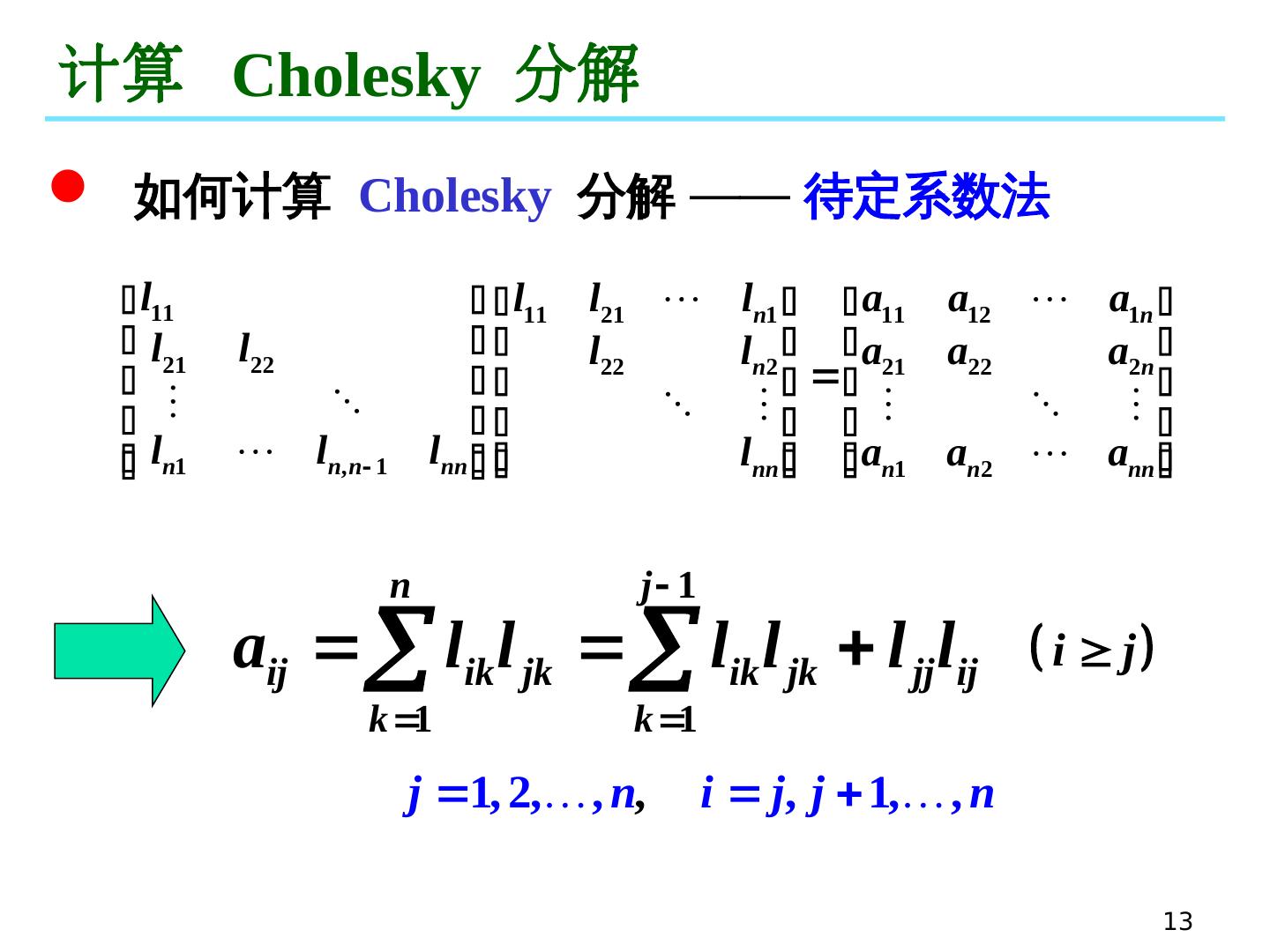
13 .13 计算 Cholesky 分解 如何计算 Cholesky 分解 —— 待定系数法

14 .14 Cholesky 分解 算法 for j = 1 to n end i = j +1, …, n 算法 ： ( Cholesky 分解 )

15 .15 平方根法 A 对称正定 先计算 A 的 Cholesky 分解 然后解方程： Ly = b 和 L T x = y i = 2, 3, …, n 算法 ： ( 解对称正定线性方程组的 平方根法 ) i = n- 1, …, 2, 1 用 Cholesky 分解求解线性方程组 —— 平方根法

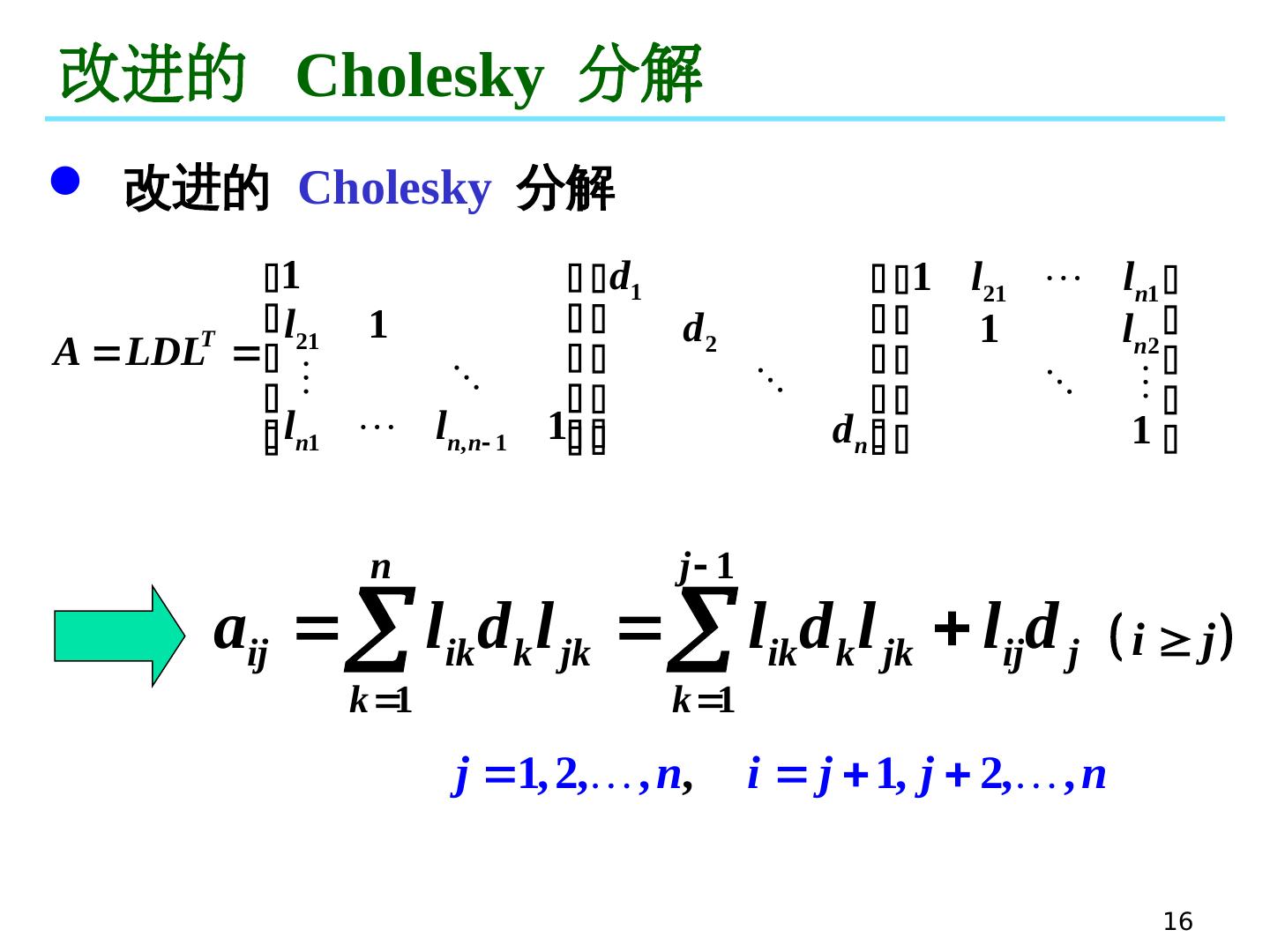
16 .16 改进 的 Cholesky 分解 改进的 Cholesky 分解

17 .17 改进 的 Cholesky 分解 for j = 1 to n end i = j +1, …, n 算法 ： ( 改进的 Cholesky 分解 ) 优点： 避免开方运算

18 .18 改进的平方根法 A 对称正定 先计算 改进的 Cholesky 分解 然后解方程组： Ly = b 和 DL T x = y i = 2, 3, …, n 算法 ： ( 解对称正定线性方程组的 改进的平方根法 ) i = n- 1, …, 2, 1 改进的平方根法

19 .19 三对角矩阵 Crout 分解 追赶 法

20 .20 三对角矩阵 LU 分解 计算过程 i = 2, 3, …, n -1 对角占优的 不可约 三对角矩阵的 Crout 分解 (1) 第一步： (2) 第二步： (3) 第三步： 为了编程方便，这里 a 的下标从 1 开始（教材是从 2 开始） 关于对角占优、不可约等性质，会在第六章详细讲述

21 .21 追赶法 A 三对角矩阵（对角占优不可约） i = 2, 3, …, n 算法 ： ( 追赶法 ) i = n- 1, …, 2, 1 i = 2, 3, …, n -1 运算量：约 5n+3n 三对角线性方程组的求解 —— 追赶法 追 追 赶

22 .22 作业 1. 教材第 177 页： 8 ， 9 ， 10 注： 第 8 题的方程组改为 ，计算精确解。 第 9 题的方程组改为 ，计算精确解。 第 10 题的方程组改为 ，计算精确解。