- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
05-Gauss 消去法
展开查看详情
1 .1 第五章 线性方程组直接解法 — Gauss 消去法
2 .2 内容提要 矩阵基础知识 Gauss 消去法 矩阵三角分解 向量与矩阵范数 误差分析
3 .3 本讲内容 向量与矩阵 特征值与谱半径 一些特殊矩阵 矩阵基础知识 Gauss 消去法 一般过程 对应的矩阵三角分解 列主元 Gauss 消去法
4 .4 线性方程组直接解法 自然科学和工程计算中 , 很多问题最终都需要求解一个或多个线性代数方程组。 (1) 直接法 : 适合低阶方程组或某些特殊大型稀疏方程组 目前常用的数值求解方法 : ( 2) 迭代法 : 解大型稀疏线性方程组的主流算法 注:在本章中,我们总是假定 A 是 n 阶非奇异方阵。
5 .5 预备知识 向量与矩阵: 定义,基本运算,行列式 特征值与特征向量,特征多项式,特征方程,矩阵相似 矩阵的谱: ( A ) = { A 的所有特征值 } 矩阵的迹: 矩阵的谱半径:
6 .6 A T 与 A 有相同的特征值,但特征向量不同 A -1 的特征值与特征向量 矩阵的迹与特征值 矩阵行列式与特征值 相似矩阵的特征值与特征向量 矩阵基本性质
7 .7 一些特殊矩阵 对角矩阵、三角矩阵、三对角矩阵 对称矩阵、 Hermite 对称矩阵、对称正定矩阵 正交矩阵、酉矩阵 初等置换阵、置换阵(排列阵) 上 Hessenberg 矩阵
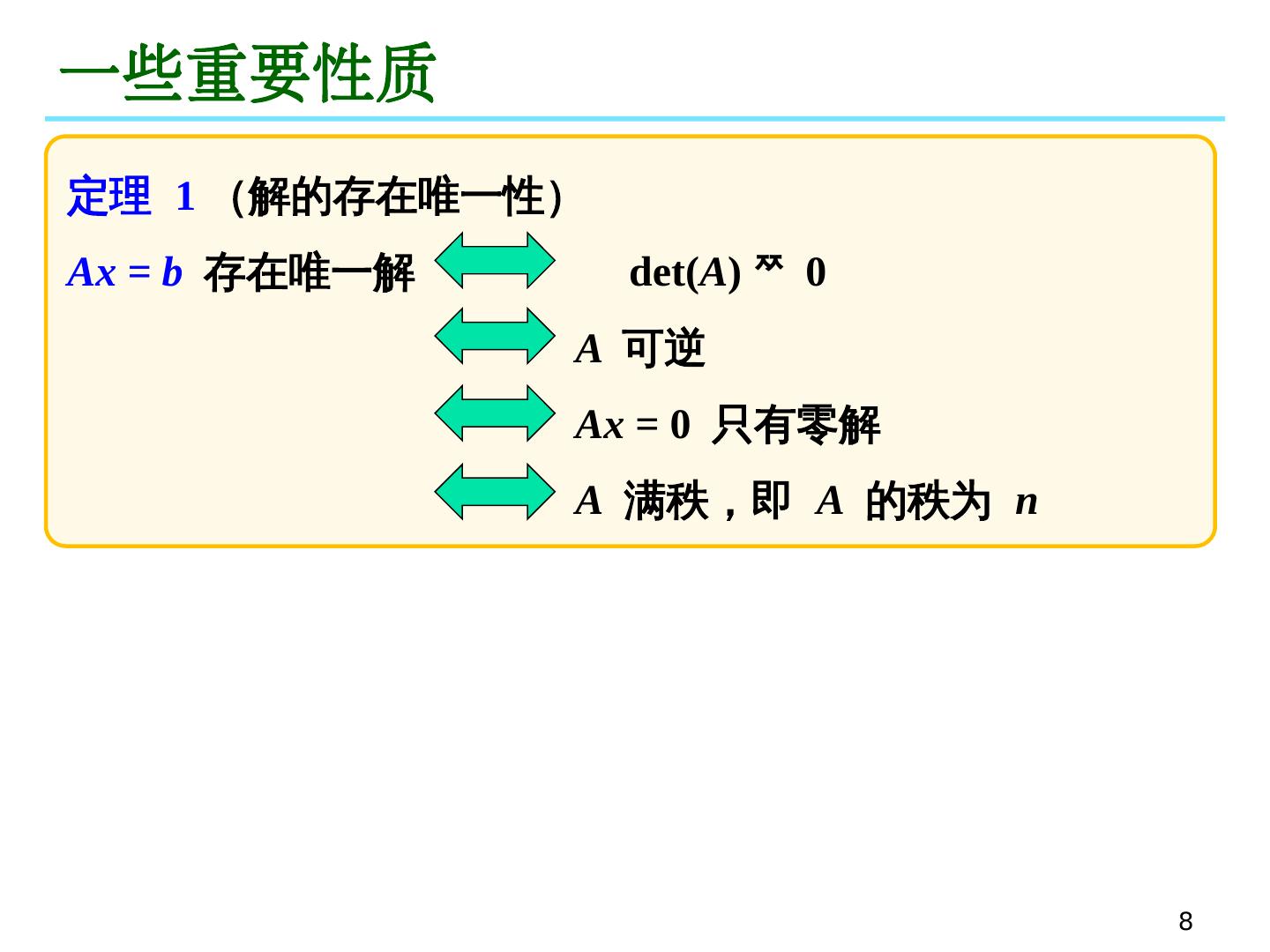
8 .8 一些重要性质 定理 1 (解的存在唯一性) Ax = b 存在唯一解 det ( A ) 0 A 可逆 Ax = 0 只有零解 A 满秩,即 A 的秩为 n
9 .9 一些重要性质 定理 2 (对称正定矩阵的性质) 若 A 对称正定,则 (1) A 非奇异,且 A 也对称正定; (2) A 的所有顺序主子矩阵都对称正定; (3) A 的所有特征值都是正实数; (4) A 的所有顺序主子式都大于 0. 定理 3 (对称正定矩阵的判定) (1) 若 A 对称,且所有顺序主子式都大于 0 ,则 A 对称正定。 (2) 若 A 对称,且所有特征值都大于 0 ,则 A 对称正定。
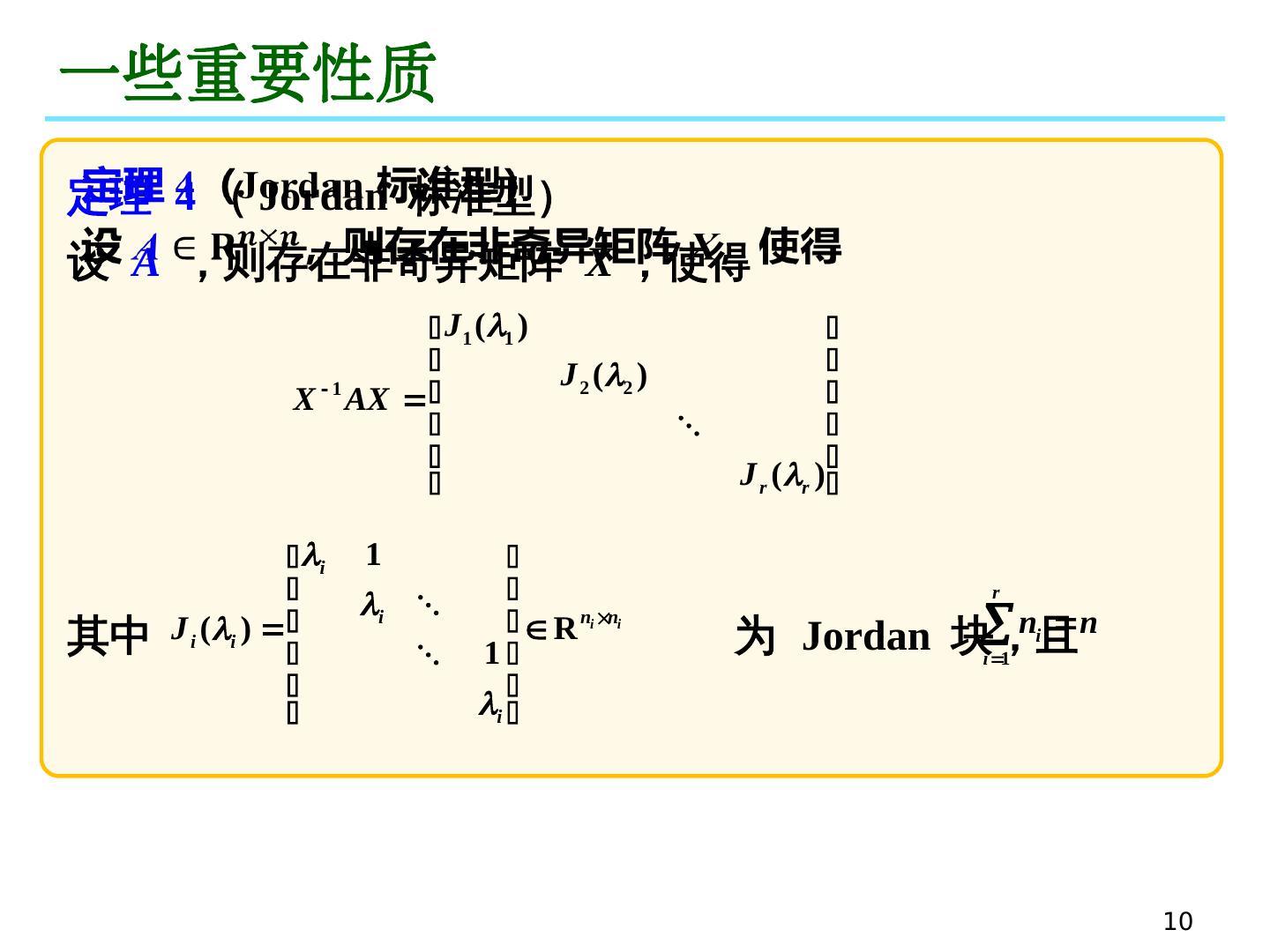
10 .10 一些重要性质 定理 4 ( Jordan 标准型) 设 A ,则存在非奇异矩阵 X ,使得 其中 为 Jordan 块,且
11 .11 Gauss 消去法 例: 用直接法解线性方程组 解:
12 .12 Gauss 消去法 高斯消去法的主要思路: 将系数矩阵 A 化为上三角矩阵,然后回代求解 考虑 n 阶线性方程组: 矩阵形式 =
13 .13 Gauss 消去法 依次将增广矩阵的 第 i 行 - m i 1 第 1 行 ,得 设 ,计算 其中 记 ,即 第 1 步:消第 1 列
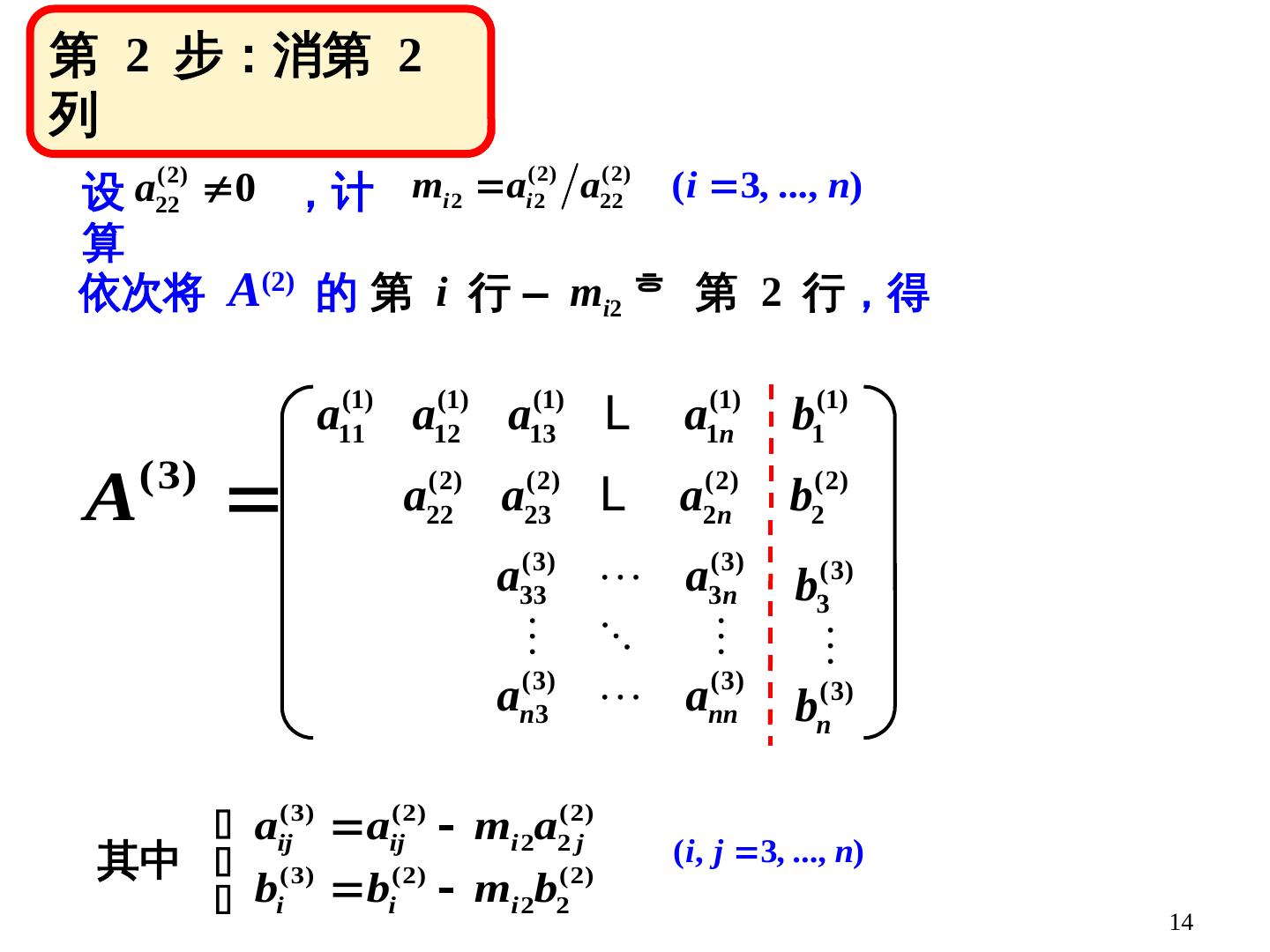
14 .14 Gauss 消去法 依次将 A (2) 的 第 i 行 – m i 2 第 2 行 ,得 其中 第 2 步:消第 2 列 设 ,计算
15 .15 Gauss 消去法 第 k 步:消第 k 列 依此类推, 第 k -1 步 后可得 设 ( i = k +1, …, n ) 先计算: 再计算: ( i = k +1, …, n )
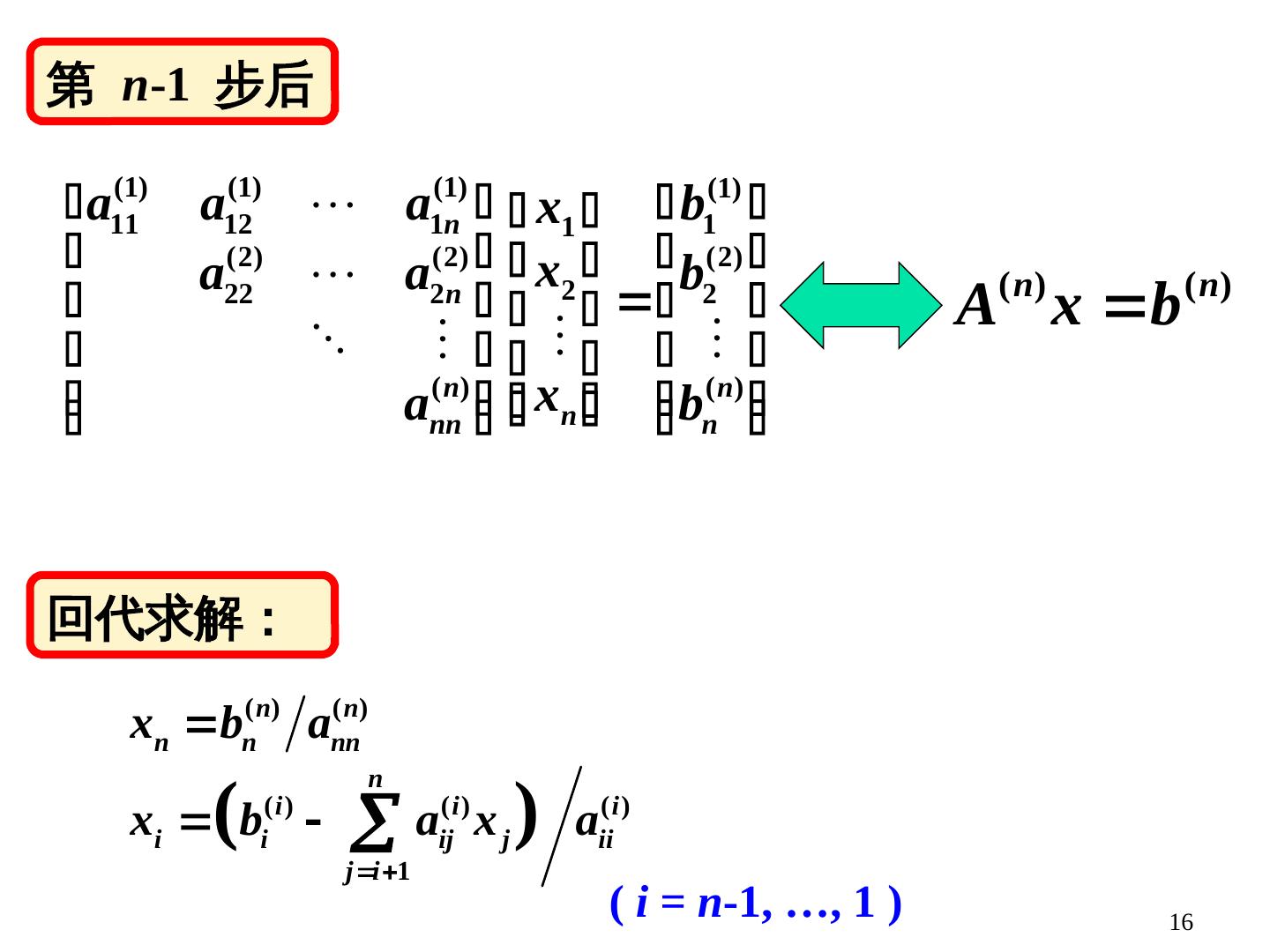
16 .16 Gauss 消去法 第 n -1 步后 回代求解: ( i = n -1, …, 1 )
17 .17 几点注记 主元: Gauss 消去法能进行到底的条件: 主元全不为 0 定理: ( i = 1, 2, ..., n ) 的充要条件是 A 的顺序主子式不为零,即 推论 :
18 .18 运算量 第 k 步: 消第 k 列 计算 计算 ( i = k +1, …, n ) 回代求解: ( i = n -1, …, 2,1 ) n – k 次 ( n – k ) 2 次 n – k 次 n ( n+ 1)/2 次 Gauss 消去法的乘除运算量为: 乘除运算 的次数 加减运算 的次数
19 .19 LU 分解 换个角度看 Gauss 消去法 矩阵的 三角分解 过程 矩阵分解 ,即将一个较复杂的矩阵分解成若干结构简单的矩阵的乘积,是矩阵计算中的一个很重要的技术。
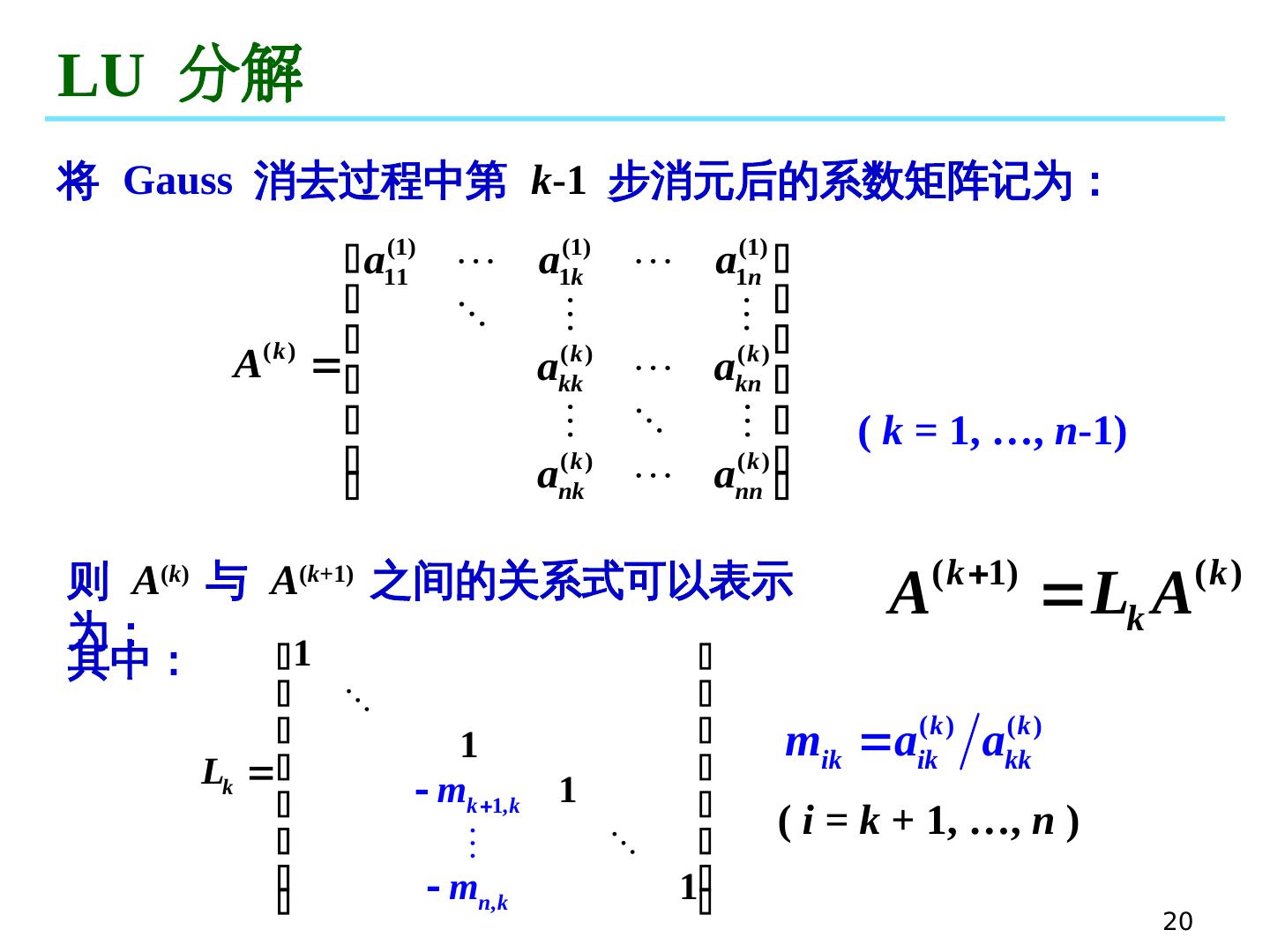
20 .20 LU 分解 则 A ( k ) 与 A ( k +1) 之间的关系式可以表示为: 其中: ( i = k + 1, …, n ) 将 Gauss 消去过程中第 k -1 步消元后的系数矩阵记为: ( k = 1, …, n -1)
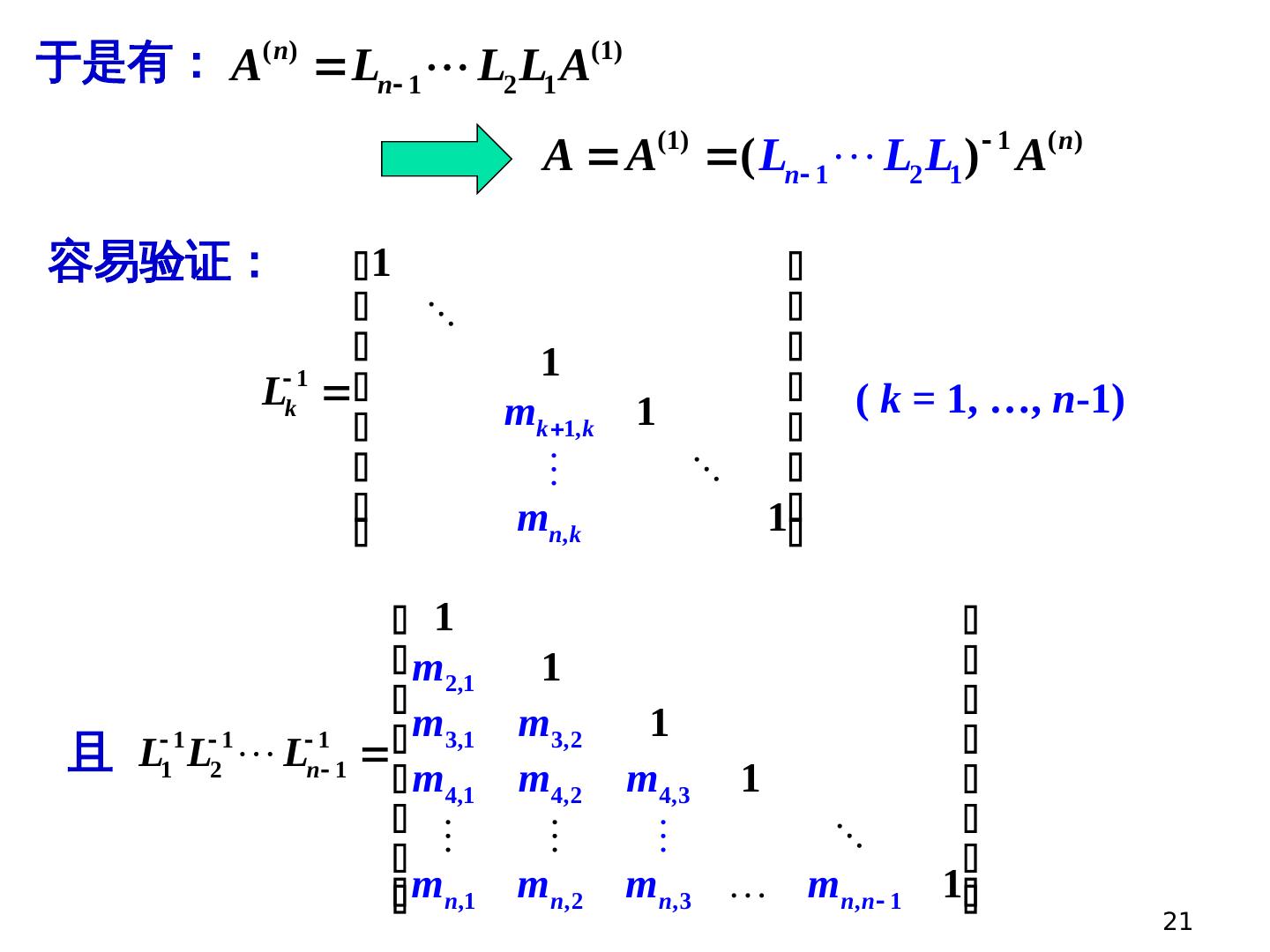
21 .21 LU 分解 LU 分解 于是有: 容易验证: ( k = 1, …, n -1) 且
22 .22 LU 分解 其中: L --- 单位下三角矩阵 , U --- 非奇异上三角矩阵 LU 分解 记: ,则 注: LU 分解中要求 L 是单位下三角, U 是非奇异上三角!
23 .23 LU 分解存在唯一性 LU 分解 存在 高斯消去法不被中断 定理: A 存在唯一的 LU 分解的充要条件是 A 的所有顺序主子式都不为零。 证明:板书 所有顺序主子式不为零
24 .24 列主元 Gauss 消去法 Gauss 消去法有效的条件是 主元全不为零! 例: 解线性方程组 ① 先选取 列主元 : ② if i k k then 交换 第 k 行 和 第 i k 行 ③ 消元 列主元 Gauss 消去法 在第 k 步消元时,在第 k 列的剩余部分选取主元 为什么要选主元?
25 .25 列主元 Gauss 消去法 算法 (列主元 Gauss 消去法 ) for k =1 to n -1 if then stop if i k k then swap k -th and i k -th row (including b ) for i = k +1 to n end end find
26 .26 PLU 分解 列主元 Gauss 消去法对应的矩阵分解为 PLU 分解 定理 :若 A 非奇异,则存在排列矩阵 P ,使得 PA = LU 其中 L 为单位下三角矩阵, U 为上三角矩阵 列主元 Gauss 消去法比普通 Gauss 消去法要多一些比较运算,但比普通高斯消去法稳定 列主元 Gauss 消去法是目前直接法的首选算法 (板书:列主元 Gauss 消去法对应的矩阵分解)
27 .27 全主元 Gauss 消去法 全主元高斯消去法 第 k 步消元时,在剩余的 n - k 阶子矩阵中选取主元 ① 先选取 全主元 : if i k k then 交换 第 k 行 和 第 i k 行 if j k k then 交换 第 k 列 和 第 j k 列 ③ 消元 列交换改变了 x i 的顺序,须记录交换次序,解完后再换回来 全主元高斯消去法具有更好的稳定性,但很费时,在实际计算中一般很少采用
28 .28 作业 1. 教材第 175 页: 1 , 2 , 5 , 7 , 11 提示: 第 5 题 : 只需 考虑 U 是下三角 情形。 第 11 题:只需判断是否存在 LU 分解,要求 L 单位下三角, U 非 奇异 上 三 角矩阵。