展开查看详情
1 .1 第四章 数值积分与数值微分 — 复合求积公式 — Romberg 算法
2 .2 本讲内容 复合梯形公式 复合 Simpson 公式 复合求积公式 Romberg （龙贝格）算法 梯形法的递推化计算 Romberg 算法基本思想 : 外推技巧 Romberg 算法 : 计算过程
3 .3 复合求积公式 提高积分计算精度的常用两种方法 用 复合公式 用 非等距节点 将积分区间分割成多个小区间 在每个小区间上使用低次 Newton-Cotes 求积公式 什么是复合求积公式 复合求积公式 复合求积公式 (Composite Numerical Integration) 也称为 复化求积公式
4 .4 复合梯形公式 将 [ a , b ] 分成 n 个小区间 [ x i , x i +1 ] ，其中 通常是 n 等分 取等距节点
5 .5 余项公式 当 x i 其中为等距节点时，即
6 .6 复合 Simpson 公式 取等距节点 注：复合 Simpson 公式实际使用了 2 n +1 个节点
7 .7 余项公式 性质： 复合梯形公式和复合 Simpson 公式都是收敛的， 也都是稳定的。
8 .8 举例 例： 设 ，利用下表中的数据分别用复合梯形公式和复合 simpson 公式计算定积分 ，并估计误差。 x i 0 1/8 2/8 3/8 4/8 5/8 6/8 7/8 1.0 f ( x i ) 1 0.997 0.990 0.977 0.954 0.936 0.909 0.877 0.841 解：
10 .10 举例 例： 计算定积分 用复合梯形公式和复合 simpson 公式时， n 分别取多大时才能使得误差不超过 0.5 10 -5 解： 要使误差不超过 0.5 10 -5 ，需要 取 n =213 复合梯形公式 213 等分
11 .11 举例 复合 simpson 公式 要使误差不超过 0.5 10 -5 ，需要 故取 n =4 8 等分
12 .12 本讲内容 复合梯形公式 复合 Simpson 公式 复合求积公式 Romberg （龙贝格）算法 梯形法的递推化计算 Romberg 算法基本思想 : 外推技巧 Romberg 算法 : 计算过程
13 .13 Romberg 算法 太 大 利用复合梯形公式、复合 simpson 公式、复合 Cotes 公式等计算定积分时， 如何选取步长 h ？ 计算精度难以保证 太 小 增加额外的计算量 解决办法：采用 变步长算法 通常采取将区间 不断对分 的方法，即取 n = 2 k ， 反复使用复合求积公式 ，直到所得到的计算结果满足指定的精度为止。
14 .x i +1/2 x i x i +1 14 梯形法递推公式 步长折半： [ x i , x i +1/2 ] ， [ x i +1/2 , x i +1 ] 将 [ a , b ] 分成 n 等分 [ x i , x i +1 ] ，
17 .17 举例 解： 例： 用梯形法的递推公式计算定积分 , 要求计算精度满足 ex42.m k T ( k ) 0 0.920735492 1 0.939793285 2 0.944513522 3 0.945690864 4 0.945985030 5 0.946058561 6 0.946076943 7 0.946081539 8 0.946082687 9 0.946082975 10 0.946083046
18 .18 梯形法的加速 但收敛速度较 慢 定理 ：设 f ( x ) C [ a , b ], 记 T n = T ( h ), 则有 梯形法递推公式算法简单，编程方便 梯形法的加速－－ 龙贝格 ( Romberg) 算法 证明：略（利用 Taylor 展开即可）
19 .19 梯形法的加速 Richardson 外推算法
20 .20 举例 例： 计算定积分 ex43.m k T 0 ( k ) 0 0.920735492 1 0.939793285 2 0.944513522 3 0.945690864 4 0.945985030 5 0.946058561 6 0.946076943 7 0.946081539 8 0.946082687 9 0.946082975 10 0.946083046
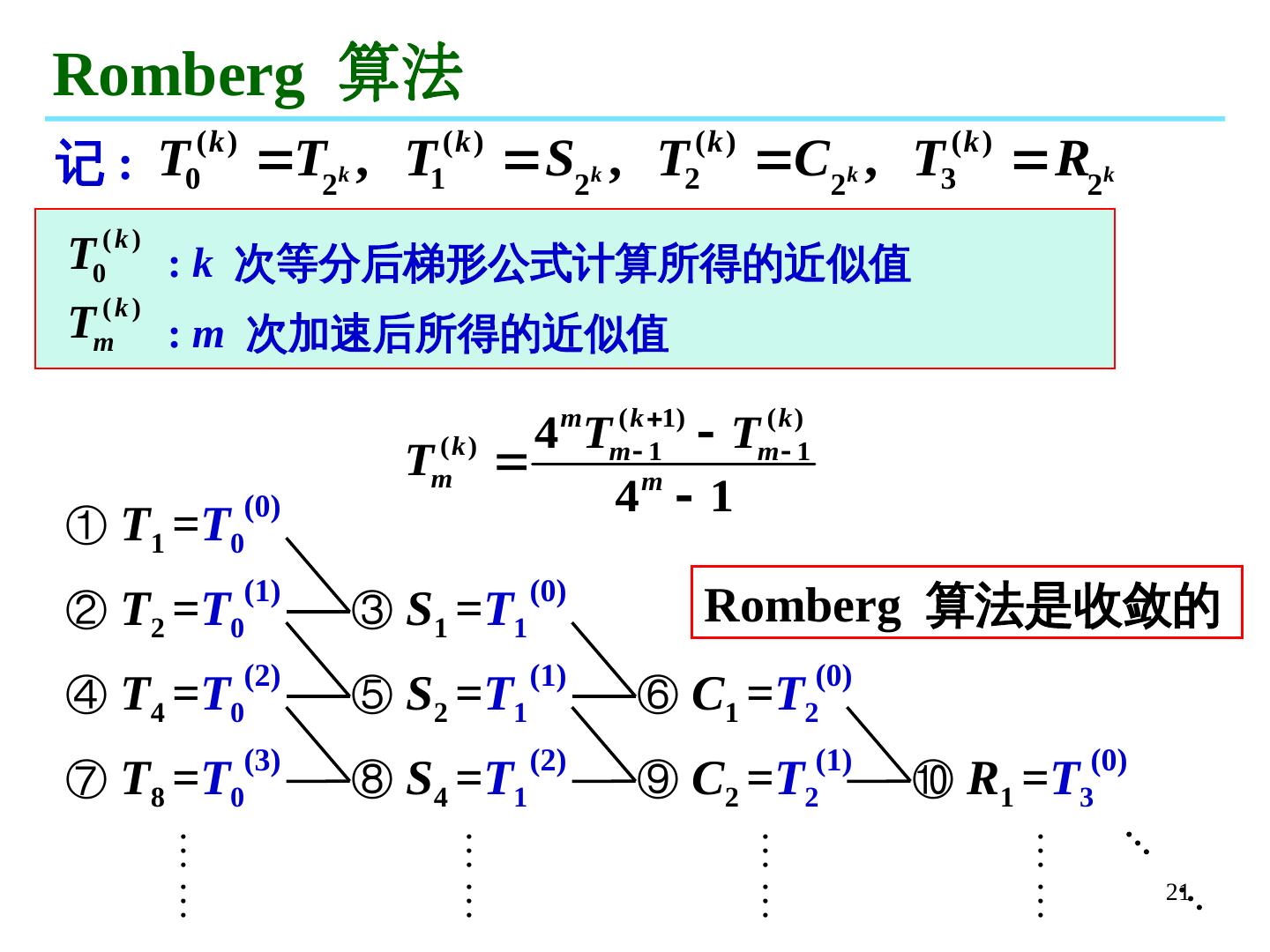
21 .21 Romberg 算法 ① T 1 = T 0 (0) ② T 2 = T 0 (1) ③ S 1 = T 1 (0) ④ T 4 = T 0 (2) ⑤ S 2 = T 1 (1) ⑥ C 1 = T 2 (0) ⑦ T 8 = T 0 (3) ⑧ S 4 = T 1 (2) ⑨ C 2 = T 2 (1) ⑩ R 1 = T 3 (0) 记: : k 次等分后梯形公式计算所得的近似值 : m 次加速后所得的近似值 Romberg 算法是收敛的
22 .22 举例 例： 用 Romberg 算法计算定积分 , 要求计算精度满足 ex44.m k 0 0.50000000 1 0.42677670 0.40236893 2 0.40701811 0.40043192 0.40030278 3 0.40181246 0.40007725 0.40005361 0.40004965 4 0.40046340 0.40001371 0.40000948 0.40000878 0.40000862 5 0.40011767 0.40000243 0.40000168 0.40000155 0.40000152 0.40000152 解： 逐步计算可得 ( k ) T 0 ( k ) T 1 ( k ) T 2 ( k ) T 3 ( k ) T 4 ( k ) T 5
23 .23 作业 1. 教材第 135 页： 2(1) ， 2(2) 注： 习题 2 (1) 积分区间改为 [0,2] ，区间等分数改为 n=4 ，计算过程中保留小数点后 3 位数字 习题 2 (2) 积分区间改为 [1,7] ，区间等分数改为 n=6 ，计算过程中保留小数点后 2 位数字
热门城市
