展开查看详情
1 .1 第四章 数值积分与数值微分 — 基本概念 — Newton-Cotes 公式
2 .2 内容提要 数值积分 数值微分 基本概念 Newton-Cotes 求积公式 复合求积公式 Romberg 求积公式 Gauss 求积公式 自适应积分方法 多重积分
3 .3 本讲内容 为什么要数值积分 数值积分基本思想 代数精度 插值型求积公式 收敛性与稳定性 数值积分基本概念 公式介绍，代数精度 余项表达式 Newton-Cotes 公式
4 .4 数值积分 微积分基本公式： ( 3) f ( x ) 表达式未知 ，只有通过测量或实验得来的数据表 但是在许多实际计算问题中 ( 2) F ( x ) 难求！ 甚至有时不能用初等函数表示。 如 (1) F ( x ) 表达式较复杂 时，计算较困难。如
5 .5 几个简单公式 矩形公式 梯形公式 抛物线公式 基本思想 （左矩形公式，左点法） （右矩形公式，右点法） （中矩形公式，中点法） （ Simpson 公式）
6 .6 数值积分一般公式 求积节点 求积系数 机械求积公式 将定积分计算转化成被积函数的 函数值 的计算 无需求原函数，易于计算机实现 一般地，用 f ( x ) 在 [ a , b ] 上的一些离散点 a x 0 < x 1 < ··· < x n b 上的函数值的加权平均作为 f ( ) 的近似值，可得 注：求积公式并不局限于机械求积公式 !
7 .7 代数精度 定义 ： 如果对于所有次数不超过 m 的多项式 f ( x ) ，求积公式 都精确成立，但对次数为 m +1 的多项式不精确成立，则称该求积公式具有 m 次代数精度 将 f ( x ) = 1, x , x 2 , … , x m 依次代入，公式精确成立 ; 将 f ( x ) = x m +1 代入，公式不精确成立。 代数精度的验证方法
8 .8 举例 例： 试确定 A i ， 使得下面的求积公式具有尽可能高的代数精度 解： 依次将 f ( x )＝ 1, x , x 2 , … , x n 代入求积公式，使其精确成立，可得 … … 存在唯一解： 所以求积公式为： 具有至少 n 次代数精度
9 .9 举例 例： 试确定系数 A i ， 使得下面的求积公式具有尽可能高的代数精度，并求出此求积公式的代数精度。 解：将 f ( x )＝1, x , x 2 代入求积公式，使其精确成立，可得 解得 A 0 =1/3, A 1 =4/3, A 2 =1/3 。所以求积公式为 将 f ( x )＝ x 3 代入可得：公式左边 =0 ，公式右边 =0 ，公式精确成立。 将 f ( x )＝ x 4 代入可得：公式左边 =2/5 ，公式右边 =2/3 ，公式不精确成立。 所以此求积公式具有 3 次代数精度。
10 .10 举例 例： ( 教材第 100 页，非机械求积公式 ) 试确定下面求积公式中的系数 ， 使其具有尽可能高的代数精度。 将 f ( x )＝ x 3 代入可得，公式左边 =1/4 ，公式右边 =1/3 ，公式不精确成立。 所以该求积公式具有 2 次代数精度。 解：将 f ( x )＝1, x , x 2 代入求积公式，使其精确成立，可得 解得 A 0 = 2/3, A 1 = 1/3, B 0 =1/ 6 。所以求积公式为
11 .11 代数精度 可以 验证： 左矩形公式 和 右矩形公式 具有 零次 代数精度 中矩形公式 和 梯形公式 具有 一次 代数精度 性质： 任意 具有 m ( 0 ) 次代数精度的机械 求积公式一定满足 练习： 抛物线公式 具有 几次 代数精度？
12 .12 插值型求积公式 设求积节点为： a x 0 < x 1 < ··· < x n b 若 f ( x i ) 已知，则可做 n 次多项式插值： 其中 余项： 其中
13 .13 插值型求积公式 当 f ( x )＝ 1, x , x 2 , … , x n 时，有 即公式精确成立 性质： 插值型求积公式具有至少 n 次代数精度 定理： 下面的求积公式具有至少 n 次代数精度的充要条件是该公式是插值型的 证明：板书 当 机械求积公式 具有尽可能高的代数精度时 , 它总是 插值型 的
14 .14 求积公式余项 注意： 教材上 101 页的公式 (1.8) 无法验证 后面所有求积公式的 余项估计都不能使用这个方法！
15 .15 求积公式的收敛性 定义 ： 如果求积公式 满足 则称该求积公式是 收敛的 。 设求积节点为： a x 0 < x 1 < ··· < x n b ，令 x i = x i – x i -1
16 .16 求积公式的稳定性 定义 ： 对 > 0 ，若存在 > 0 ，使得当 ( i = 0, 1, … , n ) 时，有 则称该求积公式是 稳定的 。 定理： 若 A i > 0, i = 0, 1, … , n ， 则下面的求积公式是稳定的 证明：板书
17 .17 Newton-Cotes 公式 基于等分节点的插值型求积公式就称为 Newton-Cotes 公式 积分区间： [ a , b ] 求积节点： x i = a + i h 求积公式： Cotes 系数
18 .18 Newton-Cotes 公式 n = 1: 代数精度 = 1 梯形公式 代数精度 = 3 n = 2: 抛物线公式 Simpson 公式 n = 4: 科特斯 ( Cotes) 公式 代数精度 = 5
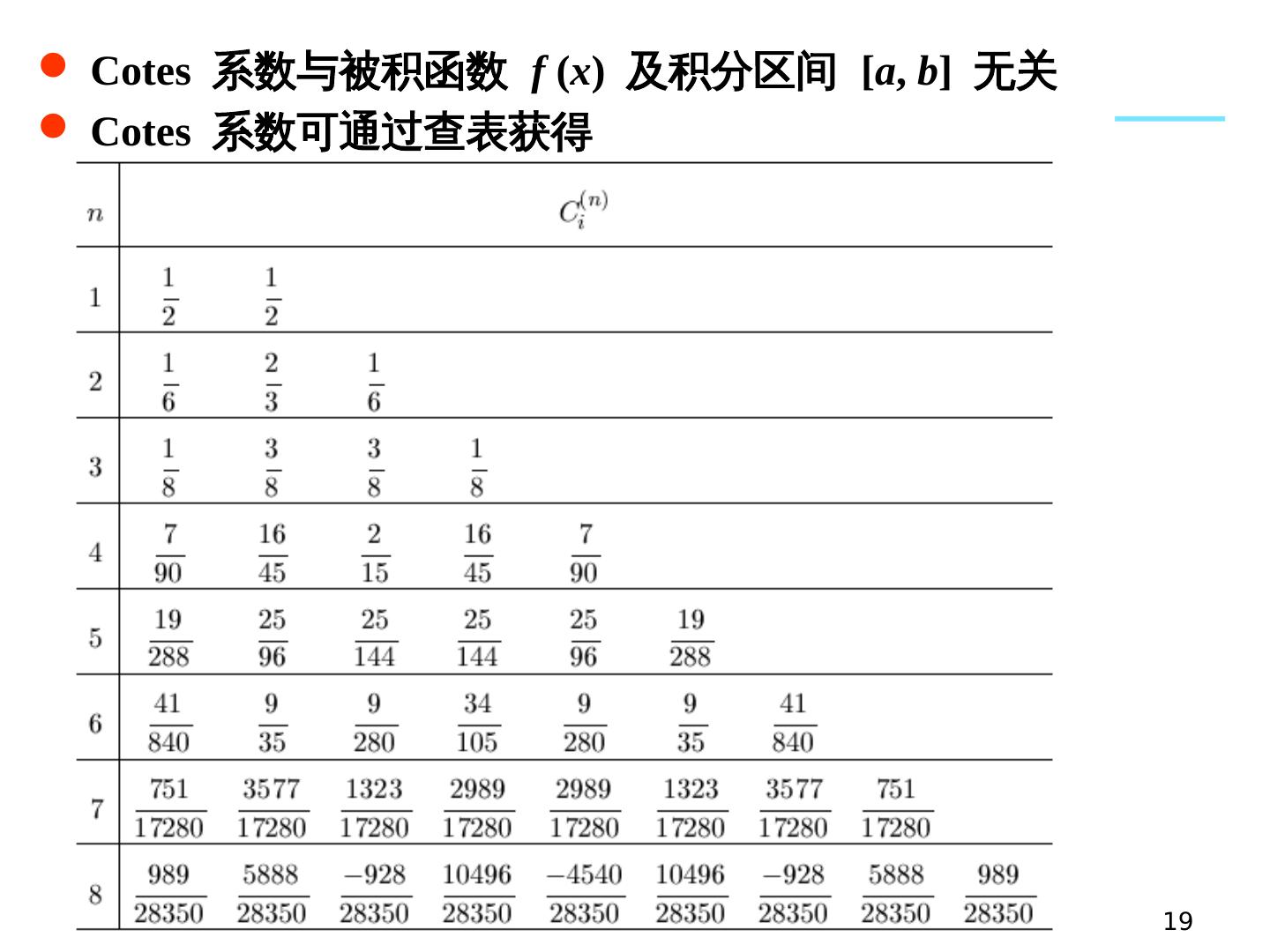
19 .19 Cotes 系数表 Cotes 系数与被积函数 f ( x ) 及积分区间 [ a , b ] 无关 Cotes 系数可通过查表获得
20 .20 N-C 公式 Cotes 系数具有以下特点： (1) (2) (3) 当 n 8 时，出现负数， 稳定性得不到保证 。而且当 n 较大时，由于 Runge 现象， 收敛性也无法保证 。 当 n 7 时， Newton-Cotes 公式是稳定的 一般不采用高阶的牛顿-科特斯求积公式
21 .21 N-C 公式代数精度 定理： 当 n 为偶数时， Newton-Cotes 公式至少有 n +1 次代数精度 定理： n 阶 Newton-Cotes 公式至少有 n 次代数精度 证： 只要证明当 n 为偶数时，公式对 f ( x )＝ x n +1 精确成立。 x = a + t h t = n - s 即
22 .22 余项估计 例： 试确定梯形公式的余项表达式 板书 例： 试确定 Simpson 公式的余项表达式 板书
23 .23 余项估计三步曲 求积公式余项估计三步曲： (1) 计算 代数精度，设为 m (2) 构造 f ( x ) 的 m 次插值多项式 p m ( x ) ，使得 ，求插值余项 注 1 ：根据求积公式中的函数值或导数值，确定插值条件 注 2 ：确保插值余项中的 n ( x ) 在求积区间内不变号 (3) 计算求积公式的余项：
24 .24 余项估计 — 非机械求积公式 例： 试确定下面的求积公式的余项表达式 板书
25 .25 N-C 公式的余项 定理： 当 n 是奇数时，设 f ( x ) C n +1 [ a , b ] ，则 N-C 公式的余项可表示为 当 n 是偶数时，设 f ( x ) C n +2 [ a , b ] ，则 N-C 公式的余项可表示为 证明：略 注： 不适用 非等步长 的求积公式和 非机械 求积公式！
26 .26 作业 1. 教材第 135 页： 1 、 4 、 5(1) 、 5(3) 、 7 注： 习题 4 的积分区间改为 [1,2] ，计算过程中保留小数点后 3 位数字，估计误差时保留 3 位有效数字。 习题 5 使用余项估计的一般方法 ，不要使用 Taylor 展开。
热门城市
