04-多重积分/数值微分

1 .1 第四章 数值积分与数值微分 — 多重积分 — 数值微分

2 .2 本讲内容 基本思想 计算方法 二重积分 问题描述 计算方法 数值微分

3 .3 二重积分 基本思想： 先化累次积分，然后数值积分

4 .4 举例 例： 用两点 Gauss 求积公式计算二重积分 令 ，可得 令 ，可得 解：

5 .5 复合公式 复合公式 为了提高计算精度，在计算累次积分时，也可以使用复合求积公式

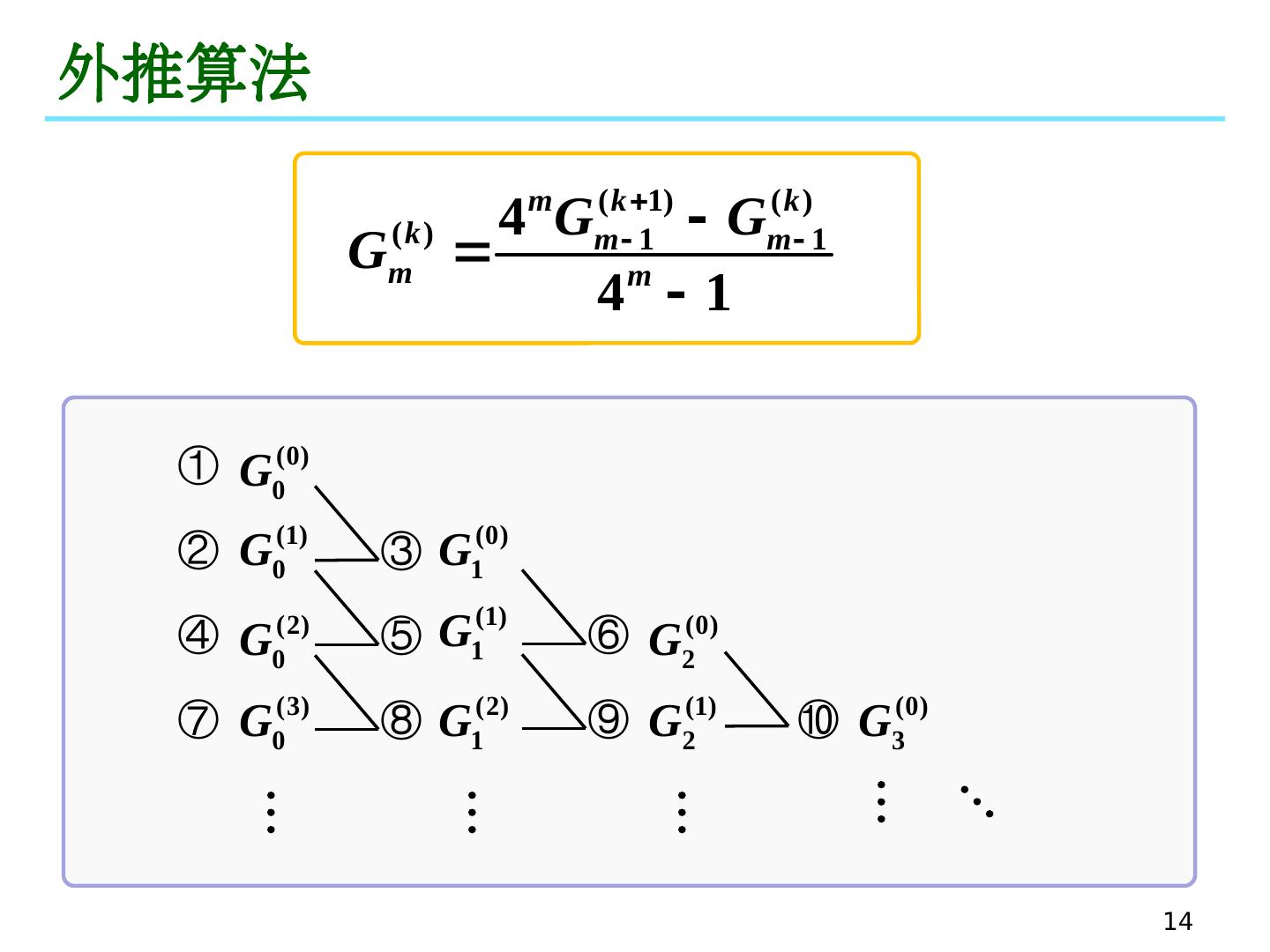
6 .6 数值微分 已知 f ( x ) 在节点 a  x 0 < x 1 < ··· < x n  b 上的函数值， 对于 [ a , b ] 中的任意一点 ， 如何计算函数在这点的导数？ 插值型求导公式 构造出 f ( x ) 的插值多项式 p n ( x ) 用 p n ( x ) 的导数来近似 f ( x ) 的导数 外推算法 基本思想： 用函数值的线性组合来近似函数的导数值

7 .7 插值型求导公式 插值型求导公式的余项 在节点 x i 处的余项 我们只考察节点处的导数值！

8 .8 两点公式 节点 x 0 , x 1 ， 步长 h = x 1 - x 0

9 .9 三点等距公式 步长 h ， 节点 x i = x 0 + ih ， i = 0, 1, 2 变量代换： x = x 0 + th

10 .10 三点等距公式 分别令 t = 0, 1, 2 , 可得

11 .11 高阶导数的近似 二阶导数的近似

12 .12 用差商近似导数 向前差商 向后差商 中心差商

13 .13 外推算法

14 .14 外推算法 ① ② ③ ④ ⑤ ⑥ ⑦ ⑧ ⑨ ⑩

15 .15 作业 1. 教材第 137 页： 17 ， 18 提示： 习题 17 ：利用插值多项式 习题 18 ，改为用三点公式计算 f ( x ) 在 x =1.2 处的一阶导数和二阶导数，并估计误差，函数值如下： f (1.1)=0.227, f (1.2)=0.207, f (1.3)=0.189