展开查看详情
2 .2 内容提要 正交多项式 正交函数族与正交多项式 Legendre 正交多项式 Chebyshev 正交多项式 Chebyshev 零点插值 第二类 Chebyshev 正交多项式（了解） Laguerre 正交多项式（了解） Hermite 正交多项式（了解）
3 .3 正交函数族 函数的正交 定义 ： 设 f ( x ), g ( x ) C [ a , b ] ， ( x ) 是 [ a , b ] 上的权函数，若 则称 f ( x ) 与 g ( x ) 在 [ a , b ] 上 带权 ( x ) 正交
4 .4 正交函数族 定义 ： 设函数 0 ( x ), 1 ( x ), , k ( x ) , C [ a , b ] ， ( x ) 是 [ a , b ] 上的权函数，若 则称 { k ( x )} 是 [ a , b ] 上 带权 ( x ) 的正交函数族 若所有 A i =1 ，则称为 标准正交函数族
5 .5 正交函数举例 例： 三角函数系 1， cos x ， sin x ， cos 2 x ， sin 2 x ， … 在 [- , ] 上是带权 ( x ) =1 的正交函数族 证： ( m, n = 1, 2, 3, … ) ( m, n = 0, 1, 2, … )
6 .6 正交多项式 定义 ： 设 n ( x ) 是 首项系数不为 0 的 n 次多项式 ， ( x ) 是 [ a , b ] 上的权函数，若 则称 为 [ a , b ] 上 带权 ( x ) 正交， 称 n ( x ) 为 n 次正交多项式。
7 .7 正交多项式 性质 1 ： 设 为 [ a , b ] 上带权 ( x ) 正交多项式， H n 为所有次数不超过 n 的多项式组成的线性空间，则 构成 H n 的一组基 性质 2 ： 设 为 [ a , b ] 上带权 ( x ) 正交多项式，则对 p ( x ) H n -1 ，有
8 .8 正交多项式 性质 3 ： 设 为 [ a , b ] 上带权 ( x ) 正交多项式，且 首项系数 均 为 1 ，则 其中 n = 0, 1, 2, … 这就是正交多项式的 三项递推公式 ！即所有 首项系数为 1 的正交多项式族都满足这个公式，该公式也给出了正交多项式的一个计算方法。 证明： 板书
9 .9 正交多项式 性质 4 ： 设 为 [ a , b ] 上带权 ( x ) 正交多项式，则 n ( x ) 在 ( a , b ) 内有 n 个不同的零点 证明： 板书
10 .10 几类重要的正交多项式 Legendre 多项式 Chebyshev 多项式 第二 类 Chebyshev 多项式（了解） Laguerre 多项式（了解） Hermite 多项式（了解）
11 .11 勒让德（ Legendre ）多项式 P n ( x ) 的首项 x n 的系数为： 在 [-1 , 1] 上带权 ( x )=1 的正交多项式称为 勒让德多项式 x [-1 , 1] ， n = 1, 2, … 记为： P 0 , P 1 , P 2 , ... 则 是 首项系数为 1 的勒让德多项式 令
12 .12 Legendre 多项式 勒让德多项式的性质 (1) 正交性： ( 3) 递推公式： 其中 P 0 ( x ) = 1, P 1 ( x ) = x ， n = 1, 2, … ( 4) P n ( x ) 在 (-1,1) 内有 n 个不同的零点 ( 2) 奇偶性： P 2 n ( x ) 只含偶次幂， P 2 n +1 ( x ) 只含奇次幂，故
13 .13 Legendre 多项式 ex31.m 勒让德多项式的表达式
14 .14 切比雪夫 （ Chebyshev ）多项式 在 [-1 , 1] 上带权 ( x ) 的正交多项式称为 切比雪夫多项式 ，其中 x [-1 , 1] ， n = 0, 1, 2, … Chebyshev 多项式 的表达式
15 .15 Chebyshev 多项式 Chebyshev 多项式 的性质 (1) 正交性： ( 3) 递推公式： 其中 T 0 ( x ) = 1, T 1 ( x ) = x ， n = 1, 2, … ( 2) 奇偶性： T 2n ( x ) 只含偶次幂， T 2n +1 ( x ) 只含奇次幂，故 cos( n +1) + cos( n -1) = 2 cos cos n x = cos
16 .16 Chebyshev 多项式 ( 4) T n ( x ) 在 (-1,1) 内有 n 个不同的零点 : ( k = 1, 2, … , n ) ( 5) T n ( x ) 在 [-1 , 1] 上有 n+1 个极值点 : ( k = 0, 1, … , n ) ( 6) T n ( x ) 的首项系数为 2 n -1 ，且 | T n ( x ) | 1
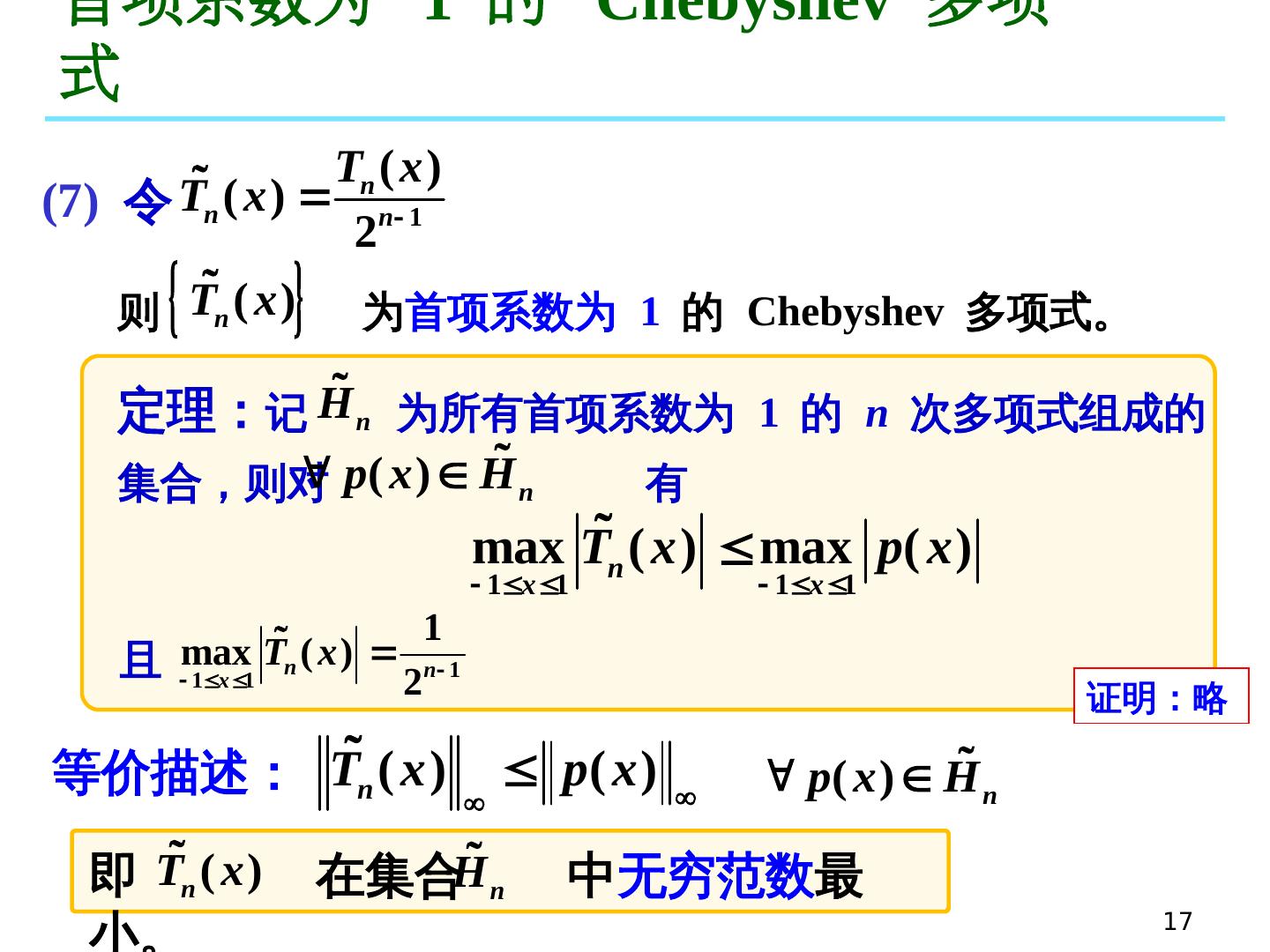
17 .17 定理： 记 为 所有首项系数 为 1 的 n 次多项式组成的集合 ，则 对 有 首项系数为 1 的 Chebyshev 多项式 ( 7) 令 则 为 首项系数为 1 的 Chebyshev 多项式。 且 即 在集合 中 无穷范数 最小。 等价描述： 证明 ：略
18 .18 首项系数为 1 的 Chebyshev 多项式 ① 这里的无穷范数是指 C[-1, 1] 上的无穷范数。 ② 定理中的结论可推广为“ 在所有次数不 超过 n 的首项系数 为 1 的 多项式中 ， 的 无穷范数最小 ” ③ 该结论可用于计算 n 次多项式在 [-1,1] 上 的 n -1 次 最佳一致逼近多项式 。 性质： 设 f ( x ) H n ，且首项系数为 a n 0 ，则 f ( x ) 在 [-1,1] 上的 n -1 次最佳一致逼近多项式为 证明：留作练习 几点注记：
19 .19 Chebyshev 多项式 例： 求 f ( x )=2 x 3 + x 2 +2 x -1 在 [-1,1] 上的 二次最佳一致逼近多项式。 解： 设 p ( x ) 是 f ( x ) 在 [-1,1] 上的 二次最佳一致逼近多项式，则由前面的性质可知 思考 ： 如何计算 n 次多项式在 [ a , b ] 上 的 n -1 次最佳一致逼近 多项式？
20 .20 Chebyshev 多项式 Chebyshev 多项式 的表达式 ex32.m
21 .21 Chebyshev 零点 插值 以 Chebyshev 多项式的 零点 作为 插值节点 进行插值 好处： 所有插值多项式中 , 总体插值误差最小 定理： 设 f ( x ) C n +1 [-1, 1] ，插值节点 x 0 , x 1 , … , x n 为 T n +1 ( x ) 的 n +1 个零点，则 用 Chebyshev 多项式的零点插值
22 .22 Chebyshev 零点 插值 若 f ( x ) C n +1 [ a , b ] ，怎么办？ 作变量替换 插值节点 ( k = 0, 1, … , n ) 插值误差
23 .23 举例 例： ( 教材 64 页，例 4) 求 在 [0 , 1 ] ，上的四次 Chebyshev 插值多项式 L 4 ( x ) ，并估计误差。 解：板书 例： ( 教材 65 页，例 5 ，上机 ) 函数 ，插值区间 [- 5, 5 ] ，试分别用等距节点和 Chebyshev 节点作 10 次多项式插值，画图比较两种插值的数值效果。 ex33.m
24 .24 其他正交多项式 第二类 Chebyshev 多项式 Laguerre 多项式 Hermite 多项式 其他 正交多项式 （了解）
25 .25 第二类 Chebyshev 第二类 Chebyshev 多项式 x [-1 , 1] ， n = 0, 1, 2, … 递推公式： 在 [-1 , 1] 上带权 正交，即 其中 U 0 ( x ) = 1, U 1 ( x ) = 2 x ， n = 1, 2, …
26 .26 Laguerre 多项式 拉盖尔（ Laguerre ） 多项式 x [ 0, ] ， n = 0, 1, 2, … 递推公式： 其中 L 0 ( x ) = 1, L 1 ( x ) = 1- x ， n = 1, 2, … 在 [ 0, ] 上带权 正交，即
27 .27 Hermite 多项式 埃尔米特（ Hermite ） 多项式 x (-,+) ， n = 0, 1, 2, … 递推公式： 其中 H 0 ( x ) = 1, H 1 ( x ) = 2 x ， n = 1, 2, … 在 (-,+) 上带权 正交，即
28 .28 作业 1. 教材第 94 页： 7 ， 8 ， 11 2. 补充题：证明 下面的结论 性质： 设 f ( x ) H n ，且首项系数为 a n 0 ，则 f ( x ) 在 [-1,1] 上的 n -1 次最佳一致逼近多项式为 提示： 第 8 题可利用正交多项式的递推公式 (P. 58, 定理 4, 注 : 该定理只对首项系数为 1 时成立 ) 注： 教材 P. 63 例 3 指的是二次最佳 一致 逼近多项式。
热门城市
