展开查看详情
2 .2 内容提要 基本概念与预备知识 正交多项式 最佳平方逼近 曲线拟合与最小二乘 有理逼近与 Pade 逼近 三角多项式逼近与快速 Fourier 变换
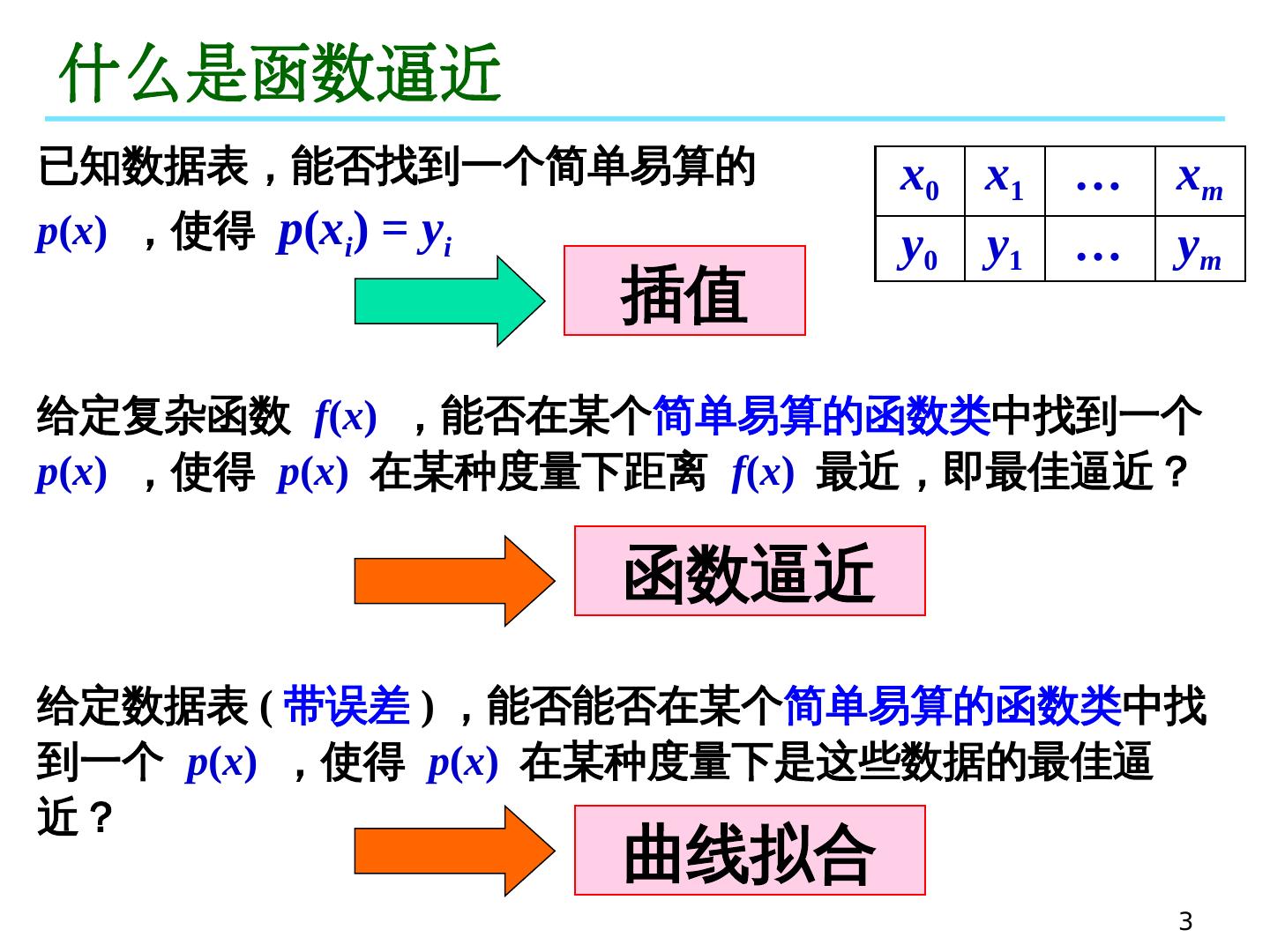
3 .3 什么是函数逼近 已知数据表，能否找到一个简单易算的 p ( x ) ，使得 p ( x i ) = y i x 0 x 1 … x m y 0 y 1 … y m 给定 复杂函数 f ( x ) ，能否 在某个 简单易算 的函数类 中 找到一个 p ( x ) ，使得 p ( x ) 在某种度量下距离 f ( x ) 最近，即最佳逼近？ 给定数据表 ( 带误差 ) ， 能否 能否 在某个 简单易算 的函数类 中 找到一个 p ( x ) ，使得 p ( x ) 在某种度量下是这些数据的最佳逼近？ 插值 函数逼近 曲线拟合
4 .4 预备知识 线性空间 范数 内积、带权内积 常见内积空间
5 . 5 预备 知识 线性空间、线性相关、线性无关 基、维数、有限维空间与无限维空间 常见线性空间： R n 、 C n 、 H n 、 C [ a , b ] 、 C n [ a , b ] 定理： （ Weierstrass 定理） 设 f ( x ) C [ a , b ] ，则对 > 0 ，总存在一个多项式 p ( x ) ，使得 在 [ a , b ] 上一致成立。 证明 ：略
6 . 6 范数与 赋范线性空间 定义： 设 S 为线性空间， x S ，若存在唯一实数 || · || ，满足 || x || 0 ， 等号当且仅当 x = 0 时成立 （正定性） || x || = | | · || x || ， R （ 齐次性 ） || x+y || || x || + || y || （三角不等式） 则称 || · || 为 S 上的范数， ( S , || · ||) 称为 赋范线性空间
7 .7 赋范线性空间 R n 线性空间 R n 上常见的范数有 1 - 范数 ： 2- 范数： - 范数（有时也称最大范数）： p - 范数：
8 .8 赋范线性空间 C[a,b] 线性空间 C [ a , b ] 上 的常见范数有 1- 范数： 2- 范数： - 范数： p - 范数：
9 .9 ， 等号当且仅当 u = 0 时成立 内积与内积空间 定义： 设 X 是数域 K ( K 可以是 R 或 C ) 上的线性空间，对 u , v X ， 有 K 中的一个数 ( u , v ) 与之对应，且满足 称 ( u , v ) 为 X 上的内积，定义了内积的线性空间称为 内积空间 实数域上的内积空间称为 欧氏空间 复数域上的内积空间称为 酉空间
10 .10 常见内 积空间 内积空间 R n 内积空间 C n 内积空间 C[ a , b ]
11 .11 正交与 Cauchy-Schwarz 不等式 定义 ： 设 X 是内 积空间 , u , v X ，若 ( u , v ) = 0 ， 则 称 u , v 正交。 定理 （ Cauchy-Schwarz 不等式 ） 设 X 是数 域 K 上 的内积空间，则对任意 u , v X ，有 思考： 等号 成立的充要条件是什么 ? 注：正交是向量相互垂直概念的推广。 证明：板书（教材有小错误）
12 .12 定理 ： G 非 奇异当且仅当 u 1 , u 2 , , u n 线性无关 。 Gram 矩阵 设 X 是内积空间， u 1 , u 2 , , u n X ，定义 Gram 矩阵 证明： 板书
13 .13 设 X 是内积空间，对任意 u X ， 定义 可以验证它是一个范数，称为 内积导出范数 。 内积与导出范数 例： R n 上的内积： 导出的范数为 ，即 2- 范数。
14 .14 设 x , y R n ，给定 正实数 1 , 2 , , n , 称 为带权 内积， 1 , 2 , , n 称为 权系数 带权内积 C n 上的带权内积 注：权系数必须全部是正数！ （思考：为什么）
15 .15 定义： 设 ( x ) 是 [ a , b ] 上的非负函数，满足 则称 ( x ) 是 [ a , b ] 上一个权函数 权函数 存在且为有限值 对 [ a , b ] 上的任意非负连续函数 g ( x ) ，满足 [ a , b ] 可以是无限区间，即 a 可以是负无穷 , b 可以 是正无穷 权函数非负 权函数与 定义区间有关 若 ， 则 ( k = 0, 1, 2, … )
17 .17 C[ a , b ] 带权内积 带权内积 设 ( x ) 是 [ a , b ] 上的权函数， f ( x ), g ( x ) C [ a , b ] 导出范数
18 .18 性质： 设 0 , 1 , , n C [ a , b ] ，则 0 , 1 , , n 线性无关当且仅当 det ( G ) 0 ，其中 G 为 Gram 矩阵，即 C[ a , b ] 带权内积
19 .19 函数逼近 最佳逼近函数 最佳逼近多项式 最佳平方逼近多项式 最佳一致逼近多项式
20 .20 函数逼近 定义： 记 为某个函数空间，给定函数 f ( x ) C [ a , b ] ，若 g* ( x ) 使得 则称 g* ( x ) 为 f ( x ) 在 中的 [ a , b ] 上的 最佳逼近函数。 什么是最佳逼近 函数逼近中的关键两点： 确定函数空间，即用什么样的函数来逼近 f ( x ) 确定度量标准，即采用什么样的评判标准
21 .21 最佳逼近多项式 定义： 记 H n 为所有次数不超过 n 的多项式组成的集合，给定函数 f ( x ) C [ a , b ] ，若 p* ( x ) H n 使得 则 称 p* ( x ) 为 f ( x ) 在 [ a , b ] 上的 n 次最佳逼近多项式 。 注 ：取不同的范数，可以定义不同的最佳逼近方式
22 .22 最佳逼近多项式 最佳一致逼近 多项式 最佳 平方逼近多项式
23 .23 曲线拟合 称 g * ( x ) 为 f ( x ) 的 最小二乘拟合 。 寻找 g* ( x ) ，使得 给定 f ( x ) C [ a , b ] 的数据表 最小二乘拟合 x 0 x 1 … x m y 0 y 1 … y m 若 = H n , 则称 g* ( x ) 为 n 次最小二乘拟合 多项式
24 .24 作业 1. 教材 第 94 页： 3 ， 4 ， 5 ， 6 提示： 第 6 题：如果 不是，说明原因；如果是，给出证明。
热门城市
