02-函数插值--分段低次插值

1 .1 第二章 函数 插值 — 分段 低次 插值

2 .为什么分段低次插值 2 高次多项式插值的病态性质： n   时 L n ( x ) 不一定收敛于 f ( x ) 插值多项式的次数并非越高越好！ 例： Runge 函数的等距节点插值多项式 ex22.m

3 .Runge 现象 3

4 .Runge 现象 4

5 .Runge 现象 5

6 .分段 低次插值 6 用 分段 低次多项式 函数来逼近原函数 f ( x ) 常见的分段低次插值 分段线性插值 分段三次 Hermite 插值 — 每个小区间上用 线性多项式 来逼近 f ( x ) — 每个小区间上用 三次 Hermite 多项式 来逼近 f ( x ) 三次样条插值 — 要求插值函数在整个插值区间上都 二阶连续可导

7 .内容提要 7 分段低次插值 分段线性插值 分段三次 Hermite 插值（两点三次 Hermite ） 三次样条插值（见下一节）

8 .8 分段 线性插值 设 a  x 0 < x 1 < ··· < x n  b 为 [ a , b ] 上的互异节点 f ( x ) 在这些节点上的函数值为 y 0 , y 1 , … , y n 记 ， 求分段函数 I h ( x ) 满足 I h ( x ) 在每个小区间 [ x k , x k+ 1 ] 上是线性函数 分段线性插值

9 .9 分段 线性插值 由以上条件直接可得 I h ( x ) 在小区间 [ x k , x k+ 1 ] 上的表达式 x  [ x k , x k+ 1 ] ， k = 0, 1, … , n -1

10 .10 误差估计 在小区间 [ x k , x k+ 1 ] 上有 当 h  0 时， I h ( x ) 在 [ a , b ] 上 一致收敛 到 f ( x ) 分段线性插值的缺点： I h ( x ) 在节点 不可导 误差估计

11 .10 误差估计 在小区间 [ x k , x k+ 1 ] 上有 当 h  0 时， I h ( x ) 在 [ a , b ] 上 一致收敛 到 f ( x ) 分段线性插值的缺点： I h ( x ) 在节点 不可导 误差估计

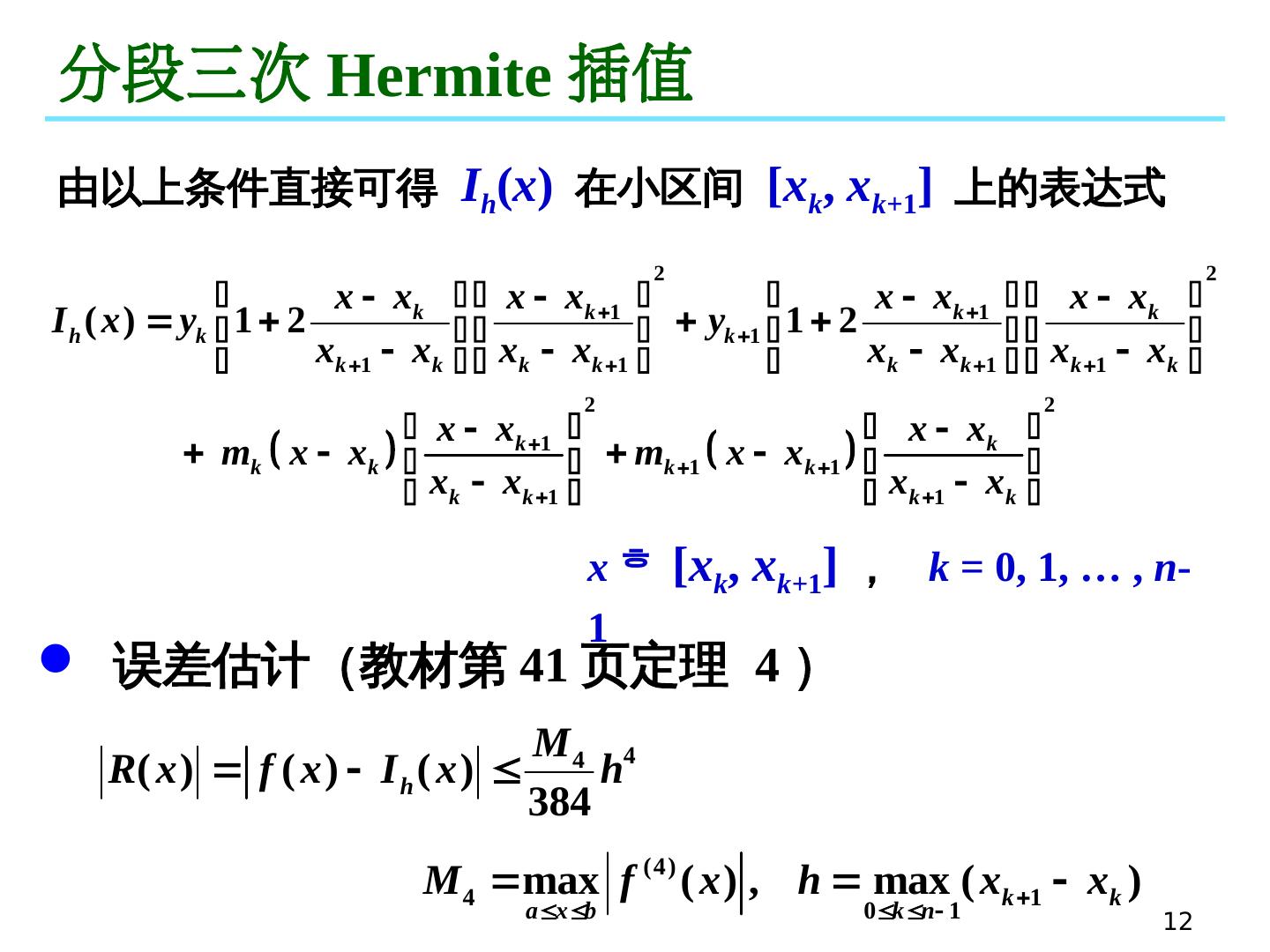
12 .12 分段 三次 Hermite 插值 由以上条件直接可得 I h ( x ) 在小区间 [ x k , x k+ 1 ] 上的表达式 x  [ x k , x k+ 1 ] ， k = 0, 1, … , n -1 误差估计（教材第 41 页定理 4 ）

13 .13 插值举例 例： 函数 ， 插值区间 [- 5, 5 ] ，取等距节点（将插值区间 10 等分），试分别用分段线性插值和分段三次 Hermite 插值画出 f ( x ) 的近似图像。 ex27.m

14 .14 分段插值注记 分段三次 Hermite 插值比分段线性插值效果更好 但公式较复杂，且需要额外信息（导数） 基本思想： 用分段低次多项式来代替单个多项式 具体作法： 优点： 公式简单 、 运算量小 、 稳定性好、收敛性 … (1) 把整个插值区间分割成多个小区间 (2) 在每个小区间上作低次插值多项式 (3) 将所有插值多项式拼接成一个多项式

15 .15 作业 1. 教材第 48 页： 15 ， 17 ， 18 ， 19 提示： 第 15 题：参考 Lagrange 插值余项公式的证明 思想。 第 17 题：写出 I h ( x ) 在小区间 [ x k , x k +1 ] 上的 表达式，分别计算 I h ( x ) 和 f ( x ) 在每个小区间中点处的值（可以借助计算器），用 表格 形式给出，误差通过 插值余项 来估计。 第 18 题和 19 题： 写出插值函数在小区间 [ x k , x k +1 ] 上的表达式即 可。 第 19 题：分段 两点三次 Hermite 插值 思考： 给出等距分段抛物插值多项式的误差上界 。