展开查看详情
1 .1 第二章 函 数 插 值 — Newton 插值
2 .为什么 Newton 插值 2 Lagrange 插值简单易用，但若要增加一个节点时，全部基函数 l k ( x ) 都需重新计算，很不方便 ! 设计一个可以逐次生成插值多项式的算法，即 p n +1 ( x ) = p n ( x ) + u n +1 ( x ) 其中 p n +1 ( x ) 和 p n ( x ) 分别为 n +1 次和 n 次插值多项式 解决办法 更换基函数 可行 方案： Newton 插值
3 .3 新的基函数 设 插值节点： x 0 , … , x n ， Newton 插值采用的基函数为： 优点： 当增加一个节点 x n+ 1 时，只需加上基函数
4 .4 Newton 插值 此时 f ( x ) 的 n 次插值多项式为 需要解决的问题 怎样确定系数 a 0 , … , a n ? 如何 从 p n ( x ) 得到 p n +1 ( x ) ? 工具： 差商 ( 均差 )
5 .内容提要 5 差商与 Newton 插值 差商（均差）及其计算方法 Newton 插值公式 差分与等距 Newton 插值
6 .6 什么是差商 设函数 f ( x ) ，节点 x 0 , … , x n f ( x ) 关于点 x i , x j 的 一阶差商 f ( x ) 关于点 x i , x j , x k 的 二阶差商 k 阶差商 差商的一般定义
7 .7 差商的性质 差商可以表示为函数值的线性组合： 用归纳法可以证明 差商与节点的排序无关，即差商具有 对称性 其中 i 0 , i 1 , … , i k 是 0 , 1, … , k 的一个任意排列 差商的等价定义： ( 教材上的所采用的定义 )
8 .8 差商的性质 k 阶差商与 k 阶导数之间的关系： 若 f ( x ) 在 [ a , b ] 上 具有 k 阶导数，则至少存在一点 ( a , b ) ， 使得 若 h ( x ) = c f ( x ) ，则 若 h ( x ) = f ( x ) + g ( x ) ，则 该 性质后面有证明
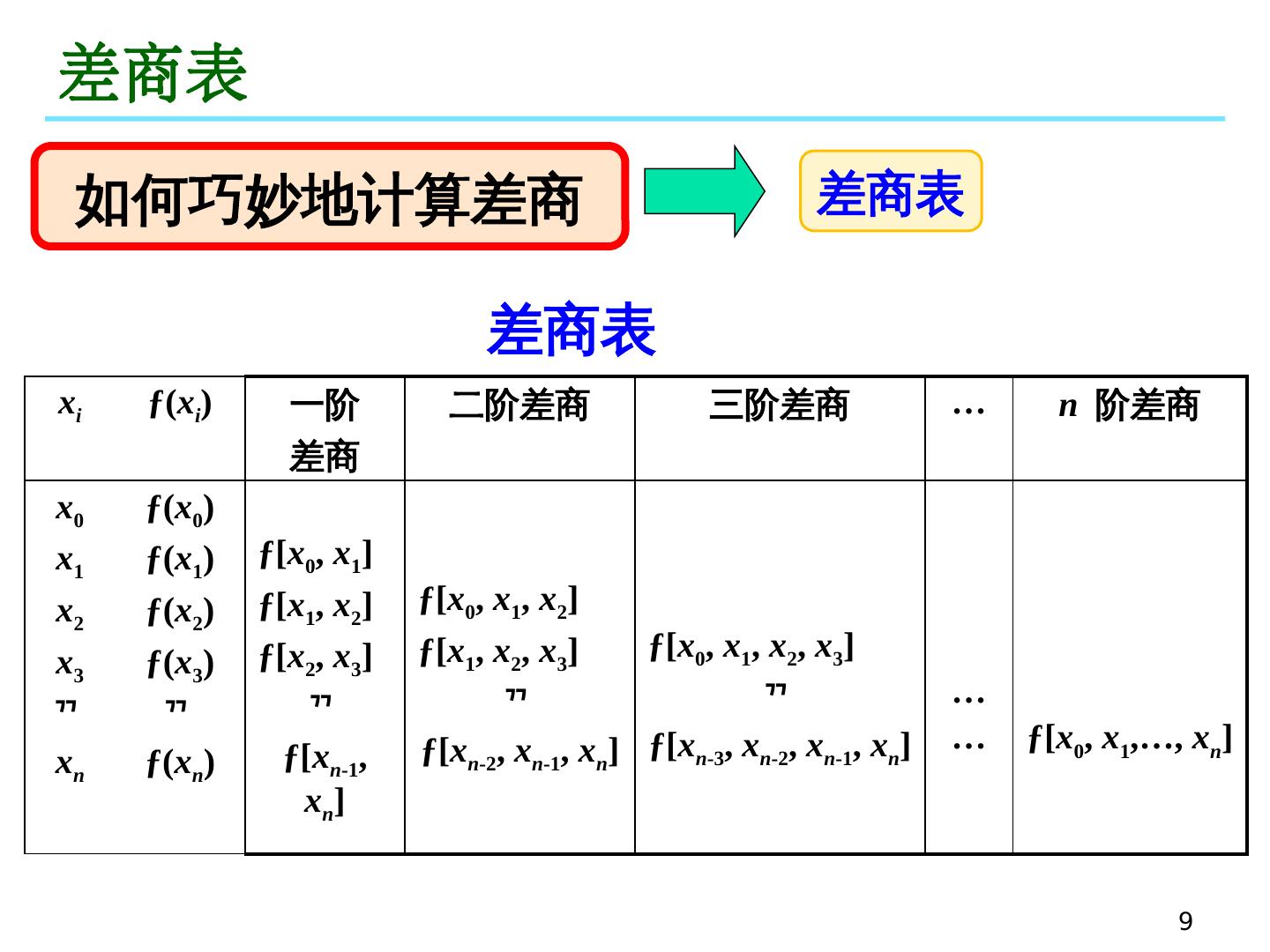
9 .9 差商表 如何巧妙地计算差商 差商表 x i ƒ( x i ) 一阶 差商 二阶差商 三阶差商 … n 阶差商 x 0 x 1 x 2 x 3 x n ƒ( x 0 ) ƒ( x 1 ) ƒ( x 2 ) ƒ( x 3 ) ƒ( x n ) ƒ[ x 0 , x 1 ] ƒ[ x 1 , x 2 ] ƒ[ x 2 , x 3 ] ƒ[ x n -1 , x n ] ƒ[ x 0 , x 1 , x 2 ] ƒ[ x 1 , x 2 , x 3 ] ƒ[ x n -2 , x n -1 , x n ] ƒ[ x 0 , x 1 , x 2 , x 3 ] ƒ[ x n -3 , x n -2 , x n -1 , x n ] … … ƒ[ x 0 , x 1 ,…, x n ] 差商表
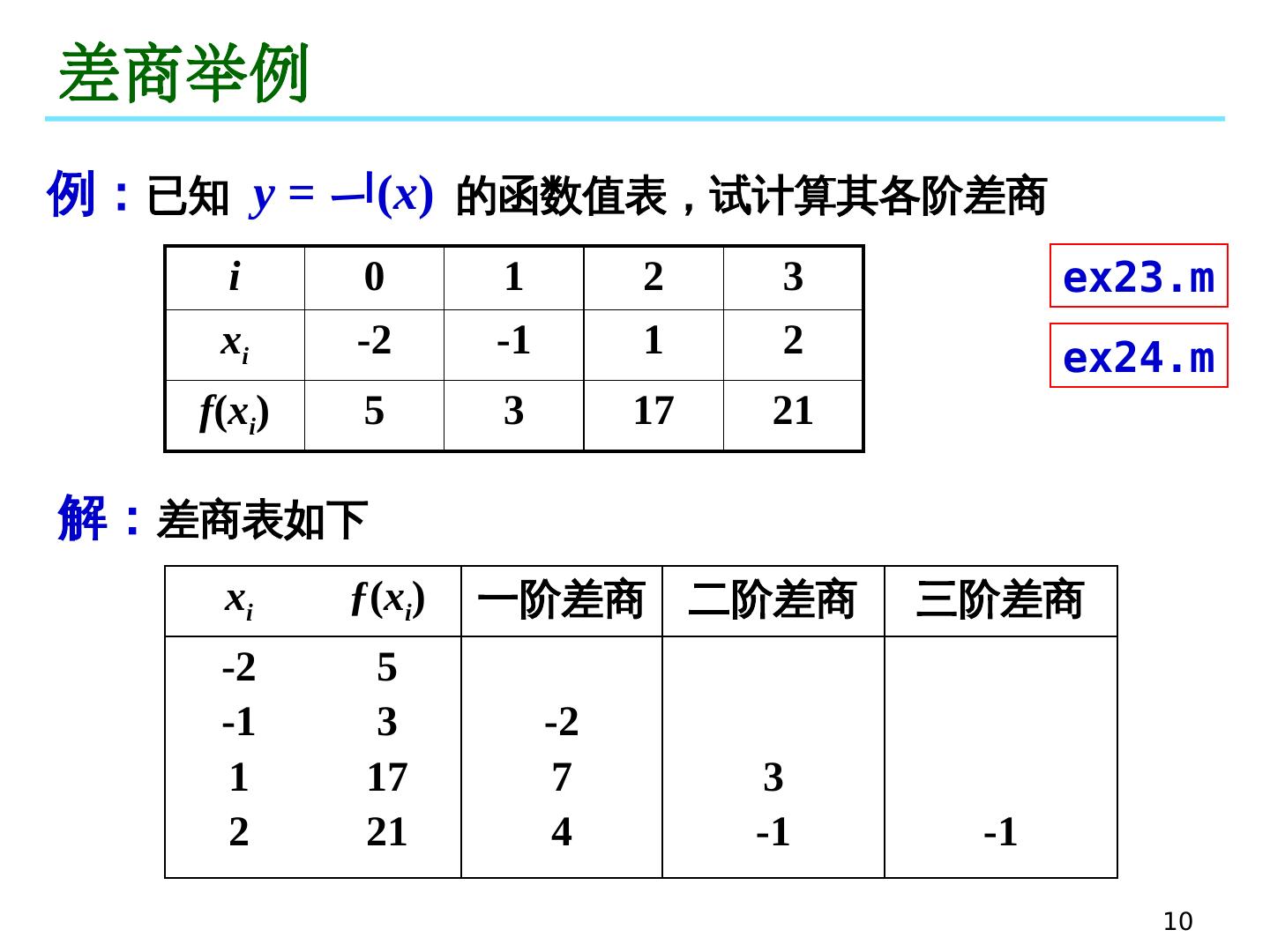
10 .10 差商举例 例： 已知 y = ( x ) 的函数值表， 试计算其各阶差商 i 0 1 2 3 x i -2 -1 1 2 f ( x i ) 5 3 17 21 解： 差商表如下 x i ƒ ( x i ) 一阶差商 二阶差商 三阶差商 -2 -1 1 2 5 3 17 21 -2 7 4 3 -1 -1 ex24.m ex23.m
11 .11 Newton 插值 公式 由差商的定义可得 1 2 … … n 1 1 + ( x x 0 ) 2 + … … + ( x x 0 )…( x x n 1 ) n 1 N n ( x ) R n ( x )
12 .12 Newton 插值 公式 f ( x ) = N n ( x ) + R n ( x ) 重要 性质： N n ( x i ) = f ( x i ) ， i = 0, 1, 2, …, n 其中 N n ( x ) 是 f ( x ) 的 n 次插值多项式
13 .13 Newton VS Lagrange N n ( x ) L n ( x ) 且余项相同 f ( x ) 在 x 0 , x 1 , … , x n 上的 n 次插值多项式是唯一的！
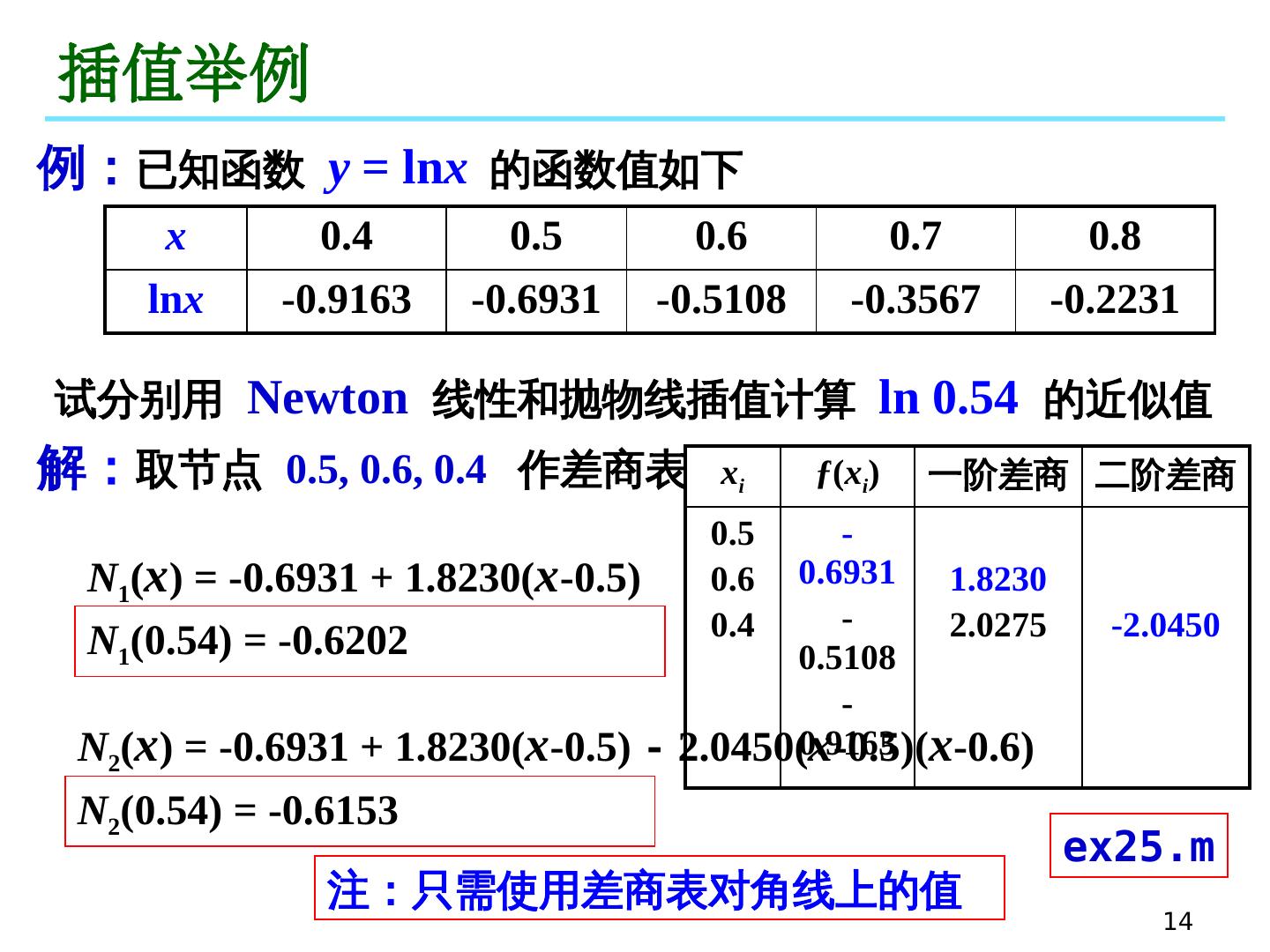
14 .14 插值举例 例： 已知函数 y = ln x 的函数值如下 解 ： 取节点 0.5, 0.6, 0.4 作差商表 试分别用 Newton 线性和抛物线插值计算 ln 0.54 的近似值 x 0.4 0.5 0.6 0.7 0.8 ln x -0.9163 -0.6931 -0.5108 -0.3567 -0.2231 x i ƒ ( x i ) 一阶差商 二阶差商 0.5 0.6 0.4 -0.6931 -0.5108 -0.9163 1.8230 2.0275 -2.0450 N 1 ( x ) = -0.6931 + 1.8230 ( x -0.5) N 1 (0.54) = -0.6202 N 2 ( x ) = -0.6931 + 1.8230 ( x -0.5) - 2.0450 ( x -0.5)( x -0.6) N 2 (0.54) = -0.6153 ex25.m 注：只需 使用差商表 对角线 上 的 值
15 .15 Newton 插值 可以看出，当增加一个节点时，牛顿插值公式只需在原来的基础上增加一项，前面的计算结果仍然可以使用。与拉格朗日插值相比，牛顿插值具有 灵活增加节点 的优点！ 注： 增加插值节点时， 须 排 在 已有插值节点的 后面 ！
16 .16 向前差分 在实际应用中，通常采用 等距 节点： x i = x 0 + i h ， i = 1, 2, …, n h> 0 ， 称为步长 此时，可以使用 差分 来简化 Newton 插值公式 向前差分（ 教材上简称为 差分 ） 定义为 f ( x ) 在 x i 处步长为 h 的 一阶向前差分
17 .17 高阶差分 二阶向前差分 n 阶向前差分 规定 高阶差分
18 .18 差分与函数值 定义不变算子 I 与移位算子 E ，即 n 阶差分的具体表达式 反之，有
19 .19 差分与 差商 之间的关系 m = 1, 2, 3, …
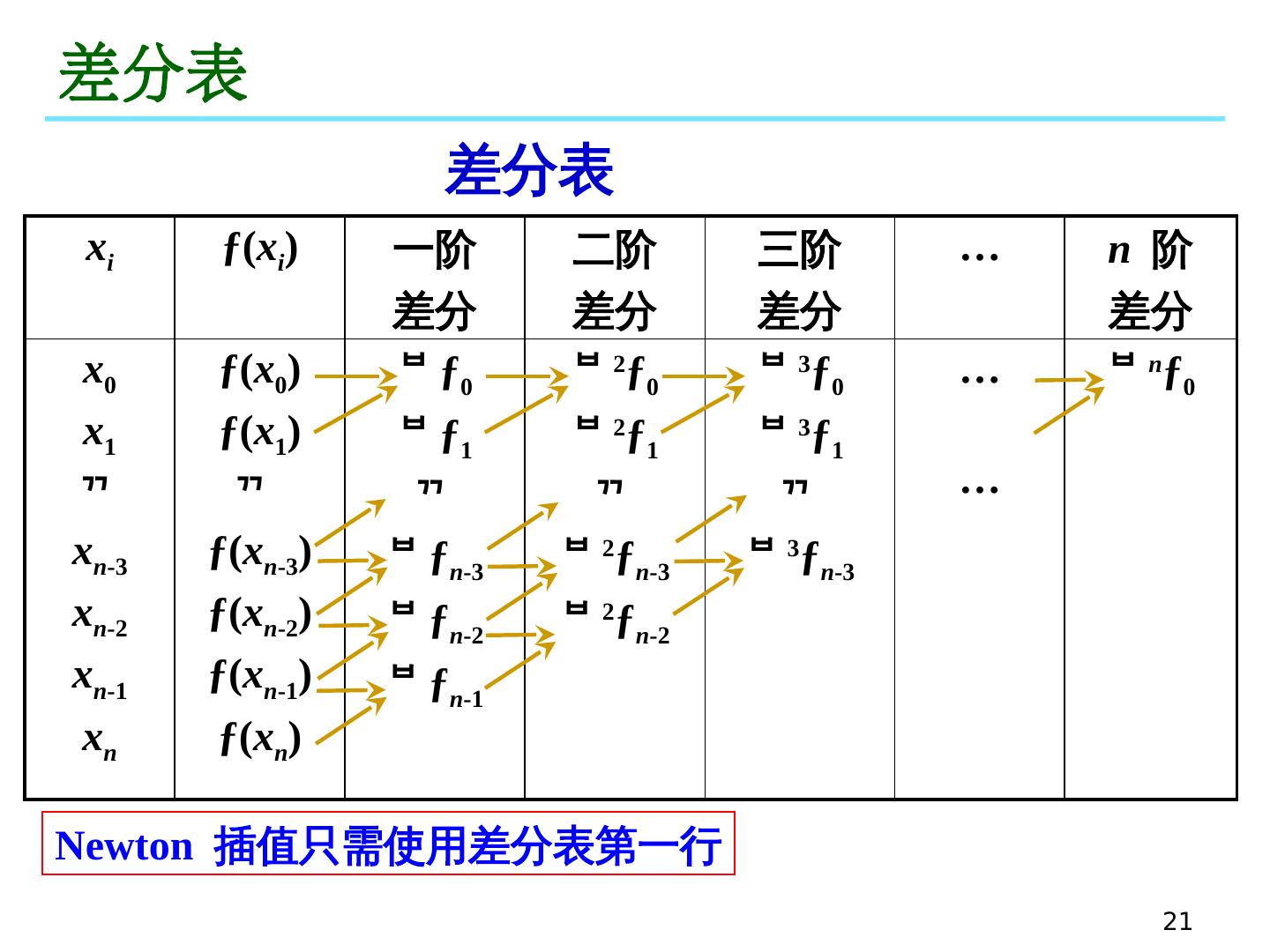
21 .21 差分表 差分表 x i ƒ( x i ) 一阶 差分 二阶 差分 三阶 差分 … n 阶 差分 x 0 x 1 x n -3 x n -2 x n -1 x n ƒ( x 0 ) ƒ( x 1 ) ƒ( x n -3 ) ƒ( x n -2 ) ƒ( x n -1 ) ƒ( x n ) ƒ 0 ƒ 1 ƒ n -3 ƒ n -2 ƒ n -1 2 ƒ 0 2 ƒ 1 2 ƒ n -3 2 ƒ n -2 3 ƒ 0 3 ƒ 1 3 ƒ n -3 … … n ƒ 0 Newton 插值只需 使用差分表第一行
22 .22 等距牛顿插值 牛顿 向前 插值 公式 设 则 用 向前差分 表示的 等距 牛顿插值公式
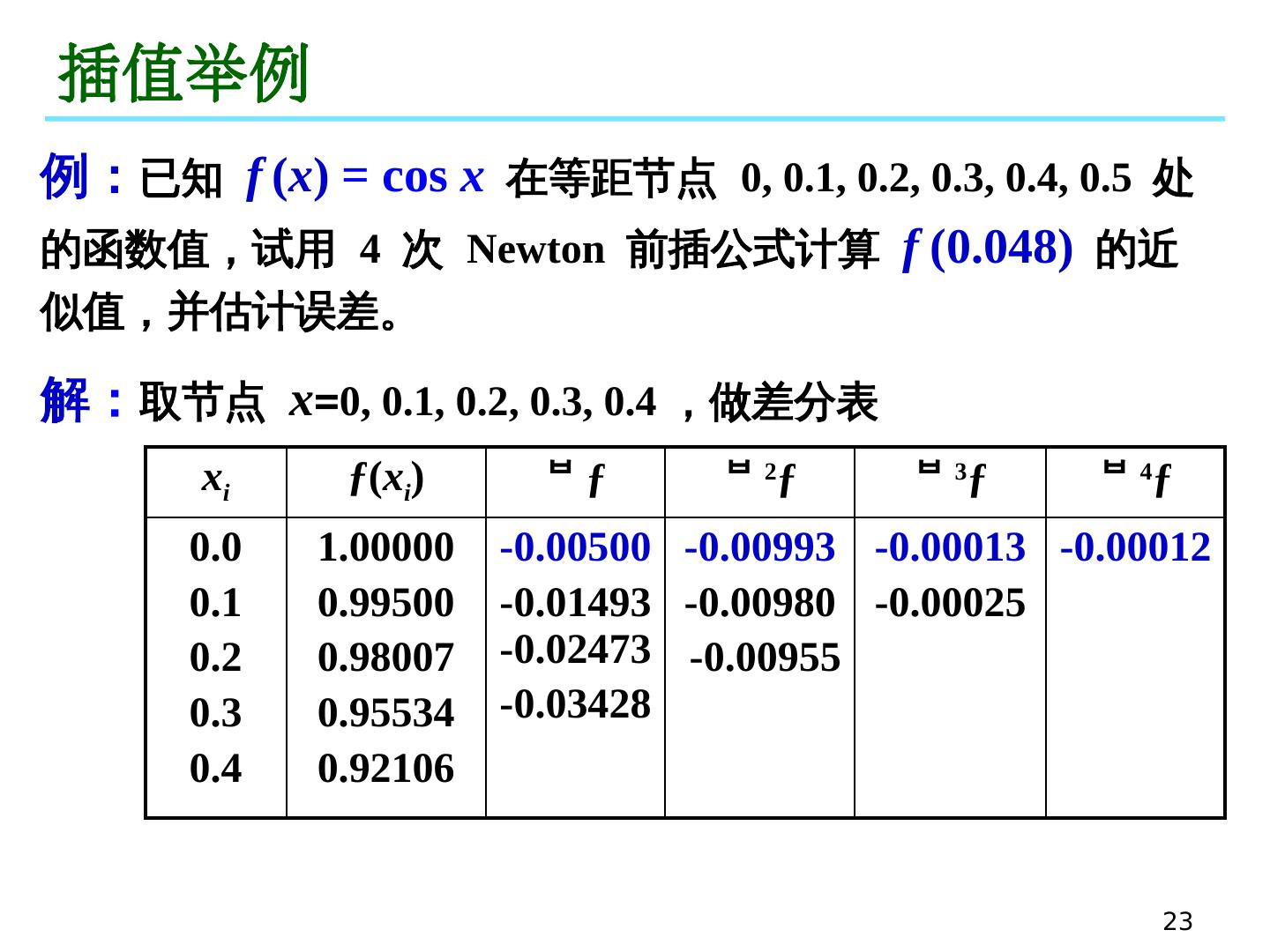
23 .23 插值举例 例 ： 已知 f ( x ) = cos x 在等距节点 0, 0.1, 0.2, 0.3, 0.4, 0.5 处的函数值，试用 4 次 Newton 前插公式计算 f (0.048) 的近似值，并估计误差。 x i ƒ ( x i ) ƒ 2 ƒ 3 ƒ 4 ƒ 0.0 0.1 0.2 0.3 0.4 1.00000 0.99500 0.98007 0.95534 0.92106 -0.00500 -0.01493 -0.02473 -0.03428 -0.00993 -0.00980 -0.00955 -0.00013 -0.00025 -0.00012 解 ： 取节点 x = 0, 0.1, 0.2, 0.3, 0.4 ，做差分表
24 .24 插值举例 ex26.m N 4 (0.048) = 1.00000 + 0.48*( - 0.00500) + = 0.99884 |R 4 (0.048)| t ( t -1) ( t -2) ( t -3) ( t -4) h 5 M 5 / 5! 1.09212 10 -7 插值点 x = 0. 048 t =( x - x 0 ) / h = 0. 48
25 .25 补充知识：向后差分 与中心差分 ( k = 1, 2, …, n ) 向 后 差分 中心 差分 ( k = 1, 2, …, n )
26 .26 作业 1. 教材 第 48 页： 1 ， 8 ， 9 ， 10 ， 12 提示： 第 1 题：单项式基底是指 1, x , x 2 第 8 题 ： 有巧妙方法， 不 要死算 第 10 题 ： 可以 利用 第 9 题的结论
热门城市
