- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
02-函数插值
展开查看详情
1 .1 第二章 函 数 插 值 — 多项式 插值 — Lagrange 插值
2 .为什么插值 2 大多数实际 问题都可用函数来表示某种内在规律的数量关系 但 函数通常无法 给出,只有通过实验或观测得到的数据表 如何根据这些数据推测或估计其它点的函数值? 例: 已测得在某处海洋不同深度处的水温如下: 深度( M) 466 741 950 1422 1634 水温( o C ) 7.04 4.28 3.40 2.54 2.13 根据这些数据,希望合理地估计出其它深度(如 500、600、 800 米…)处的水温。 数学工具 :数值插值技术
3 .如果存在一个 简单易算 的函数 p ( x ) , 使得 p ( x i ) = f ( x i ), i = 0, 1, ... , n 则称 p ( x ) 为 f ( x ) 的 插值函数 什么是插值 3 已知函数 y = f ( x ) 在 [ a , b ] 上有定义,且已经测得在点 a x 0 < x 1 < ··· < x n b 处的函数值为 y 0 = f ( x 0 ),… , y n = f ( x n ) [ a , b ] 为插值区间, x i 为插值节点, p ( x i ) = f ( x i ) 为插值条件 插值节点 无需递增排列 ,但必须确保 互不相同 ! 求插值函数 p ( x ) 的方法就称为 插值法
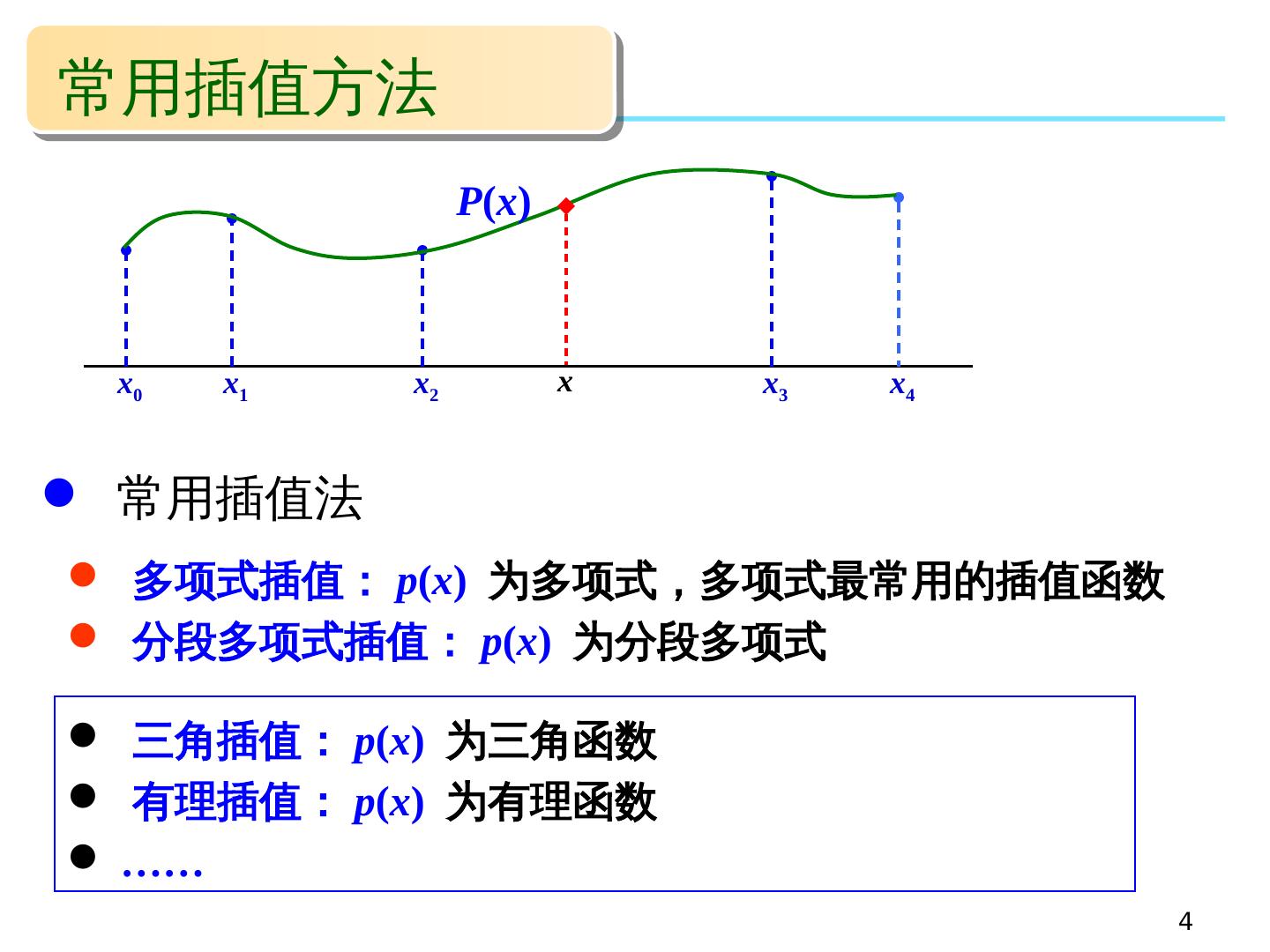
4 .常用插值方法 4 x 0 x 1 x 2 x 3 x 4 x 多项式插值: p ( x ) 为多项式,多项式最常用的插值函数 分段多项式插值 : p ( x ) 为分段多项式 三角插值: p ( x ) 为三角函数 有理插值: p ( x ) 为有理函数 …… P ( x ) 常用插值法
5 .内容提要 5 多项式插值 Lagrange 插值 差商与 Newton 插值 Hermite 插值 分段低次插值 三次样条插值
6 .6 多项式插值 多项式插值 已知函数 y = f ( x ) 在 [ a , b ] 上 n + 1 个点 a x 0 < x 1 < · · · < x n b 处的函数值为 y 0 = f ( x 0 ),… , y n = f ( x n ) 求次数 不超过 n 的多项式 p ( x ) = c 0 + c 1 x + · · · + c n x n , 使得 p ( x i ) = y i , i = 0, 1, ... , n 注意: p ( x ) 的次数有可能小于 n
7 .7 多项式插值 定理 (多项式插值的存在唯一性) 满足上述条件的多项式 P ( x ) 存在且唯一。 注:该定理的证明过程事实上也给出了一种求 p ( x ) 的方法,但较复杂,一般不用!后面将给出较简单的求法 证明 :板书( Vandermonde 行列式)
8 .线性插值 例 ( 板书 ): 线性插值,即求一次多项式 p ( x ) ,满足 p ( x 0 ) = y 0 , p ( x 1 ) = y 1 p ( x 0 ) = y 0 p ( x 1 ) = y 1 点斜式 重新整理 我们注意到, p ( x ) 是两个一次多项式的线性组合 令 则 进一步观察可知: 为什么能写成这个形式?
9 .9 抛物线插值 例: 抛物线插值,即 求二次 多项式 p ( x ) ,满足 p ( x 0 ) = y 0 , p ( x 1 ) = y 1 , p ( x 2 ) = y 2 想法:如果能构造三个二次多项式 l 0 ( x ), l 1 ( x ), l 2 ( x ), 满足 问题:如何构造 l 0 ( x ), l 1 ( x ), l 2 ( x ) ? 待定系数法
10 .10 内容提要 多项式插值 Lagrange 插值 差商与 Newton 插值 Hermite 插值 分段低次插值 三次样条插值 基函数法 Lagrange 基函数 Lagrange 插值余项与误差估计
11 .11 基函数插值法 基函数 插值法 通过基 函数来构造 插值多项式的方法 就 称为 基函数 插值 法 记 Z n ( x ) = { 次数不超过 n 的多项式的全体 } n +1 维 设 z 0 ( x ), z 1 ( x ), ... , z n ( x ) 构成 Z n ( x ) 的一组基,则插值多项式可表示为 p ( x ) = a 0 z 0 ( x ) + a 1 z 1 ( x ) + · · · + a n z n ( x ) 寻找合适的基函数 确定插值多项式在这组基下的线性表示系数
12 .12 Lagrange 插值 Lagrange 基函数 定义: 设 l k ( x ) 是 n 次多项式, 在节点 x 0 , x 1 , … , x n 上满足 则 称 l k ( x ) 为节点 x 0 , x 1 , … , x n 上的 n 次 Lagrange 插值 基函数 通过构造法,可求得
13 .13 Lagrange 插值 两点说明 l 0 ( x ) , l 1 ( x ) , … , l n ( x ) 构成 Z n ( x ) 的一组 基 l 0 ( x ) , l 1 ( x ) , … , l n ( x ) 与插值节点有关,但与 f ( x ) 无关
14 .14 Lagrange 插值 如何用 Lagrange 基函数求 P ( x ) 设 p ( x ) = a 0 l 0 ( x ) + a 1 l 1 ( x ) + · · · + a n l n ( x ) 将 p ( x i ) = y i , i = 0, 1, ... , n 代入,可得 a i = y i , i = 0, 1, ... , n p ( x ) = y 0 l 0 ( x ) + y 1 l 1 ( x ) + · · · + y n l n ( x ) L n ( x ) 就称为 f ( x ) 的 Lagrange 插值多项式
15 .15 线性与抛物线插值 两种特殊情形 线性插值多项式(一次插值多项式): n = 1 抛物线插值多项式(二次插值多项式): n = 2 注: n 次插值多项式 L n ( x ) 通常是 n 次的,但有时也会低于 n 次。如:二次插值中,如果三点共线,则 L n ( x ) 为直线
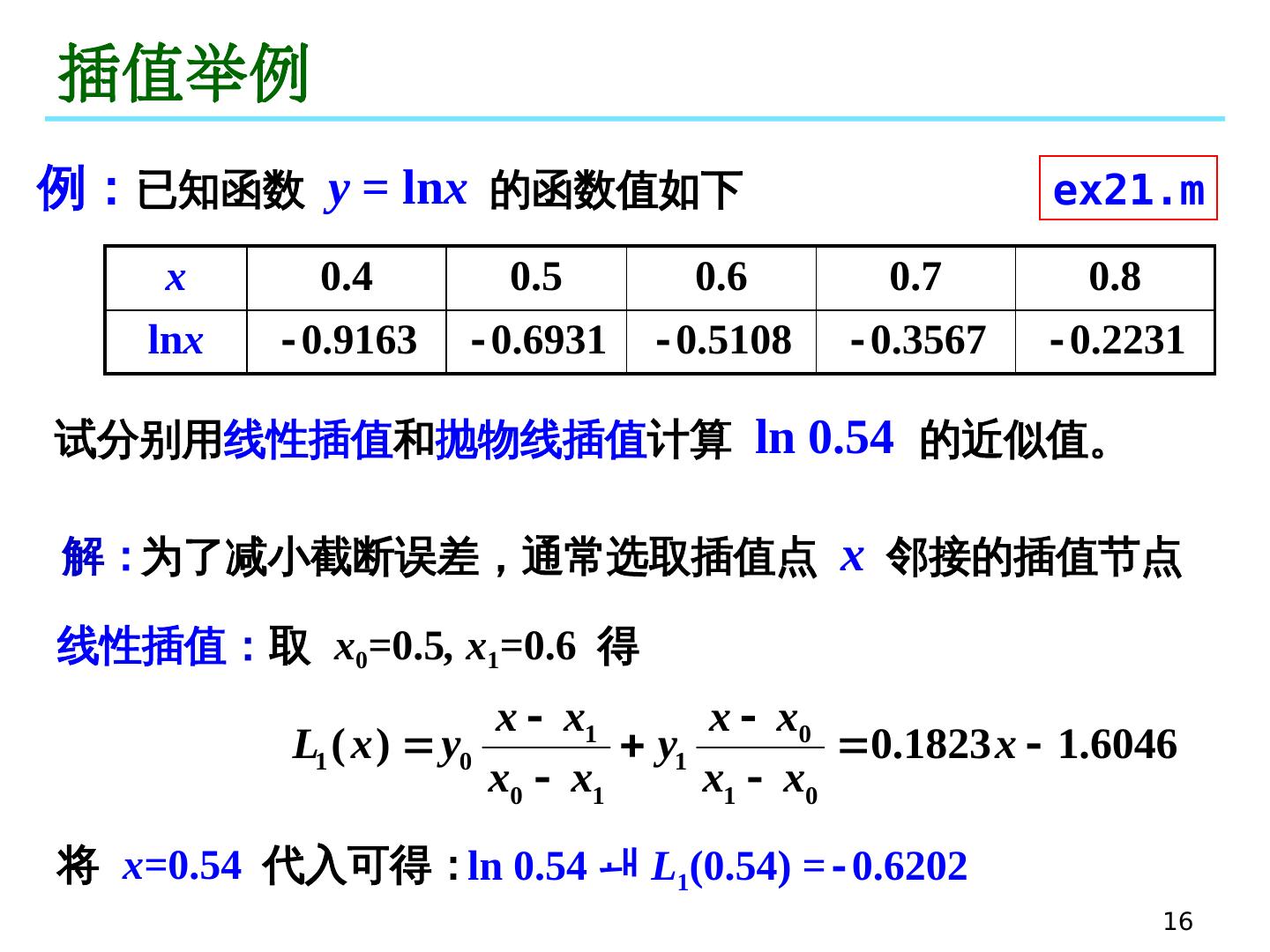
16 .16 插值举例 例: 已知函数 y = ln x 的函数值如下 解 : x 0.4 0.5 0.6 0.7 0.8 ln x - 0.9163 - 0.6931 - 0.5108 - 0.3567 - 0.2231 试分别用 线性插值 和 抛物线插值 计算 ln 0.54 的 近似值。 线性插值 : 取 x 0 = 0.5 , x 1 = 0.6 得 将 x= 0.54 代入可得: ln 0.54 L 1 (0.54) = - 0.6202 为了减小截断误差,通常选取插值点 x 邻接的插值节点 ex21.m
17 .17 插值举例 抛物线插值 : 取 x 0 = 0.4 , x 1 = 0.5 , x 2 = 0.6, 可得 ln 0.54 L 2 (0.54) = - 0.6153 在实际计算中,一般不需要给出插值多项式的具体表达式 ln 0.54 的精确值为: - 0.616186 ··· 可见,抛物线插值的精度比线性插值要高 Lagrange 插值简单方便,只要取定节点就可写出基函数,进而得到插值多项式,易于计算机 实现。
18 .18 误差估计 估计误差 插值余项 定理: 设 f ( x ) C n [ a , b ] ( n 阶连续可微 ) ,且 f ( n +1) ( x ) 在 ( a , b ) 内存在,则对 x [ a,b ] ,存在 x ( a , b ) 使得 其中 证明 : 板书 注:余项中的 x 与 x 是相关的
19 .19 插值余项 由插值条件可知: R n ( x i )=0, i =0, 1, …, n R n ( x ) 在[ a , b ] 上至少有 n +1 个零点 对任意给定的 x [ a,b ] ( x x i , i =0, 1, ..., n ) ,构造辅助函数 则 在 [ a, b ] 中有 n +2 个互不相同的零点: x, x 0 , … , x n R n ( x ) 可写成 罗尔 定理
20 .20 插值余项 由 Rolle 定理 可知 在 ( a , b ) 内至少有 n +1 个不同的零点; 同理可知 在 ( a , b ) 内至少有 n 个零点; 又 条件: f ( x ) C n [ a , b ] ,且 f ( n +1) ( x ) 在 ( a , b ) 内存在 以此类推,可知 在 ( a , b ) 内至少有一个零点,设为 x , 即 , x ( a , b ) 。
21 .21 插值余项 线性插值(两点插值,即 n =1 ) 两个特例 抛物线插值(三点插值,即 n =2 )
22 .22 插值余项 余项公式只有当 f ( x ) 的高阶导数存在时才能使用 几点说明 计算点 x 上的近似值时,应尽量选取与 x 相近插值节点 若 , 则 x 与 x 有关,通常无法确定 , 实际使用中通常是估计其上界
23 .23 Lagrange 基函数性质 Lagrange 基函数的两个重要性质 当 f ( x ) 为一个次数 n 的多项式时,有 故 即 n 次插值多项式对于次数 n 的 多项式是 精确 的 若 f ( x ) = x k , k n ,则有 特别地,当 k = 0 时有
24 .24 插值误差举例 例: 已知函数 y = ln x 的函数值如下 x 0.4 0.5 0.6 0.7 0.8 ln x - 0.9163 - 0.6931 - 0.5108 - 0.3567 - 0.2231 试估计 线性插值 和 抛物线插值 计算 ln 0.54 的误差 解 : 线性插值 x 0 = 0.5 , x 1 = 0.6, (0.5, 0.6)
25 .25 插值误差举例 抛物线插值 : x 0 = 0.4 , x 1 = 0.5 , x 2 = 0.6, (0.4, 0.6) 抛物线插值 通常 优于线性插值。 但绝对不是次 数越高就越好, 嘿嘿 …
26 .26 插值误差举例 例: 函数 ,插值区间 [- 5, 5 ] ,取等距节点, 试画出插值多项式 L 的图像 ex22.m 例 : 设 l i ( x ) 是关于点 x 0 , x 1 , … , x 5 的 Lagrange 插值基函数 . 证明 : 证明 : 板书
27 .27 插值误差举例 例 : 设 f ( x ) C 2 [ a , b ] (二 阶 连续可导) , 证明 : 其中 板书
28 .28 作业 教材第 48 页: 3 、 4 (2) 、 5 、 6 提示: 第 3 题: ① 等距 节点 插值,假定节点上的函数值是已知的; ② 将 度数转化为弧度,要 考虑插值误差和所给数据的舍入误差 第 6 题:等距 节点 插值 ,假定节点上的函数值是已知 的,且没有误差