01-线性代数基础

1 .第一讲 线性代数基础 1 向量范数与矩阵范数 2 矩阵与投影 3 矩阵标准型 4 数值域 5 Chebyshev 多项式 

2 .1 向量范数与矩阵范数 1.1 向量范数 1.2 矩阵范数 1.3 序列的收敛 2/67 

3 .1.1 向量范数 定义 1 (向量范数) 若函数 f : Cn → C 满足 (1) f (x) ≥ 0, ∀ x ∈ Cn 且等号当且仅当 x = 0 时成立; (非负性, nonnegativity) (2) f (αx) = |α| · f (x), ∀ x ∈ Cn , α ∈ C (正齐次性, homogeneity) (3) f (x + y) ≤ f (x) + f (y), ∀x, y ∈ Cn ; (三角不等式, triangular inequality) 则称 f (x) 为 Cn 上的 范数 (norm ), 通常记作 ∥ · ∥. † 相类似地, 我们可以定义实数空间 Rn 上的向量范数. † 如果 f 只满足 f (x) ≥ 0, 正齐次性和三角不等式, 则称为 半范数 (seminorm ). 例 1 常见的向量范数: • 1-范数: ∥x∥1 = |x1 | + |x2 | + · · · + |xn |; √ • 2-范数: ∥x∥2 = |x1 |2 + |x2 |2 + · · · + |xn |2 ; • ∞-范数: ∥x∥∞ = max |xi |; 1≤i≤n ( )1/p ∑ n • p-范数: ∥x∥p = |xi |p , 1 ≤ p < ∞. i=1 容易证明, 任何一个内积都可以定义一个相应的范数. √ 推论 1 设 (·, ·) 是 Cn 上的内积, 则 ∥x∥ (x, x) 是 Cn 上的一个向量 范数. 3/67 

4 .定义 2 (范数的等价性) 设 ∥ · ∥α 与 ∥ · ∥β 是 Cn 空间上的两个向量范数, 若存在正常数 c1 , c2 , 使得 c1 ∥x∥α ≤ ∥x∥β ≤ c2 ∥x∥α 对任意 x ∈ Cn 都成立, 则称 ∥ · ∥α 与 ∥ · ∥β 是等价的. 定理 2 Cn 空间上的所有向量范数都是等价的, 特别地, 有 √ ∥x∥2 ≤ ∥x∥1 ≤ n ∥x∥2 , ∥x∥∞ ≤ ∥x∥1 ≤ n ∥x∥∞ , √ ∥x∥∞ ≤ ∥x∥2 ≤ n ∥x∥∞ . † 有限维赋范线性空间上的所有范数都是等价的. 定理 3 (Cauchy-Schwartz 不等式) 设 (·, ·) 是 Cn 上 的 内 积, 则 对 任 意 x, y ∈ Cn , 有 |(x, y)|2 ≤ (x, x) · (y, y) 且等号成立的充要条件是 x 与 y 线性相关. 更一般地, 我们有下面的 Holder 不等式. 定理 4 (Holder 不等式) 设 (·, ·) 是 Rn 上 的 Euclidean 内 积, 则 对 任 意 x, y ∈ Rn , 有 |(x, y)|2 ≤ ∥x∥p · ∥y∥q , 1 1 其中 p, q > 0, 且 + = 1. p q 4/67 

5 .定理 5 (范数的连续性) 设 ∥ · ∥ 是 Cn 上的一个向量范数, 则 f (x) ∥x∥ 是 Cn 上的连续函数. 5/67 

6 .1.2 矩阵范数 定义 3 若函数 f : Cm×n → C 满足 (1) f (A) ≥ 0, ∀ A ∈ Cm×n 且等号当且仅当 A = 0 时成立; (2) f (αA) = |α| · f (A), ∀ A ∈ Cm×n , α ∈ C; (3) f (A + B) ≤ f (A) + f (B), ∀A, B ∈ Cm×n ; 则称 f (x) 为 Cm×n 上的范数, 通常记作 ∥ · ∥. 设 ∥ · ∥ 是 Cm×n 上的范数, 若对任意 A ∈ Cm×n 和任意 x ∈ Cn , 有 ∥Ax∥ ≤ ∥A∥ · ∥x∥, (1.1) 则称矩阵范数 ∥ · ∥ 与向量范数相容, 这里的 ∥Ax∥ 和 ∥x∥ 分别为 Cm 和 Cn 上的向量范数. † 类似地, 我们可以定义 Rm×n 上的矩阵范数. 设 f 是 Cn×n 上的范数, 如果 f 还满足 (4) f (AB) ≤ f (A)f (B), ∀ A, B ∈ Cn×n 则称 f 是相容的矩阵范数. † 在本讲义中, 如果不加特别指出, 所涉及的矩阵范数都是指相容的矩 阵范数. 例 2 常见的矩阵范数: • F -范数 ∑ n ∑ n ∥A∥F = |aij |2 ; i=1 j=1 • p-范数 ∥Ax∥p ∥A∥p = sup . x̸=0 ∥x∥p 6/67 

7 .一类常用的矩阵范数就是由向量范数导出的算子范数. 引理 1 (算子范数, 诱导范数, 导出范数) 设 ∥ · ∥ 是 Rn 上的向量范数, 则 ∥Ax∥ ∥A∥ sup = max ∥Ax∥ x∈Rn , x̸=0 ∥x∥ ∥x∥=1 是 Rn×n 上的范数, 称为算子范数, 或诱导范数, 导出范数. 引理 2 可以证明: ( n ) ∑ (1) 1-范数 (列范数): ∥A∥1 = max |aij | ; 1≤j≤n  i=1  ∑ n (2) ∞-范数 (行范数): ∥A∥∞ = max  |aij | ; 1≤i≤n j=1 √ (3) 2-范数: ∥A∥2 = ρ(A A) . 计算 2-范数时需要求谱半径, 因此通常比计算 1-范数和 ∞-范数更困难. 但在某些情况下可以用下面的范数等价性来估计一个矩阵的 2-范数. 定理 6 (矩阵范数的等价性) Rn×n 空间上的所有范数都是等价的, 特别 地, 有 1 √ √ ∥A∥1 ≤ ∥A∥2 ≤ n ∥A∥1 , n 1 √ √ ∥A∥∞ ≤ ∥A∥2 ≤ n ∥A∥∞ , n 1 ∥A∥∞ ≤ ∥A∥1 ≤ n ∥A∥∞ , n 1 √ √ ∥A∥1 ≤ ∥A∥F ≤ n ∥A∥2 . n 除此之外, 我们还有下面的性质. 7/67 

8 .引理 3 设 A ∈ Rn×n , 则 ∥A∥22 ≤ ∥A∥1 · ∥A∥∞ , 且 max {|aij |} ≤ ∥A∥2 ≤ n max {|aij |}. 1≤i,j≤n 1≤i,j≤n 定理 7 范数的性质: (1) 对任意相容范数 ∥ · ∥, 有 ∥Ak ∥ ≤ ∥A∥k ; (2) 对任意算子范数 ∥ · ∥, 有 ∥Ax∥ ≤ ∥A∥ · ∥x∥, ∥AB∥ ≤ ∥A∥ · ∥B∥, 即算子范数是相容范数; (3) ∥Ax∥2 ≤ ∥A∥F · ∥x∥2 , ∥AB∥F ≤ ∥A∥F · ∥B∥F , 即 F -范数是相容 范数; (4) F -范数不是算子范数; (5) ∥ · ∥2 和 ∥ · ∥F 是酉不变范数, 即对任意酉矩阵 U , V , 有 ∥U A∥2 = ∥AV ∥2 = ∥U AV ∥2 = ∥A∥2 , ∥U A∥F = ∥AV ∥F = ∥U AV ∥F = ∥A∥F (6) ∥A ∥2 = ∥A∥2 , ∥A ∥1 = ∥A∥∞ ; (7) 若 A 是正规矩阵, 则 ∥A∥2 = ρ(A), 因此, ∥A∥2 ≤ ∥A∥, 其中 ∥ · ∥ 是任意算子范数. 8/67 

9 .1.3 序列的收敛 首先给出向量序列收敛的定义. { }∞ 定义 4 (向量序列的收敛) 设 x(k) k=1 是 Cn 中的一个向量序列. 如果 存在向量 x = [x1 , x2 , . . . , xn ] ∈ Cn 使得 (k) lim xi = xi , i = 1, 2, . . . , n, k→∞ (k) { } 其中 xi 表示 x(k) 的第 i 个分量. 则称 x(k) (按分量) 收敛到 x, 即 x 是 x(k) 的极限, 记为 lim x(k) = x. k→∞ 相类似地, 我们可以给出矩阵序列收敛的定义. { [ ]}∞ (k) 定义 5 (矩阵序列的收敛) 设 A(k) = aij 是 Cm×n 中的一个矩 k=0 阵序列. 如果存在矩阵 A = [aij ] ∈ Cm×n 使得 (k) lim aij = aij , i = 1, 2, . . . , m, j = 1, 2, . . . , n, k→∞ 则称 A(k) 收敛到 A, 即 A 是 A(k) 的极限, 记为 lim A(k) = A. k→∞ 关于向量序列和矩阵序列的收敛性, 我们有下面的结论 [268]. { [ ]}∞ 定理 8 设向量序列 {x(k) }∞ (k) k=0 ⊂ C , 矩阵序列 A ⊂ n (k) = aij k=0 C m×n ,则 (1) lim x(k) = x ⇐⇒ lim ∥x(k) − x∥ = 0, 其中 ∥ · ∥ 为任一向量范 k→∞ k→∞ 数; (2) lim A(k) = A ⇐⇒ lim ∥A(k) − A∥ = 0, 其中 ∥ · ∥ 为任一矩阵 k→∞ k→∞ 9/67 

10 . 范数; (3) lim A(k) = 0 ⇐⇒ lim A(k) x = 0, ∀ x ∈ Rn . k→∞ k→∞ 下面是关于 收敛速度 的定义. 定义 6 设点列 {εk }∞ k=1 收敛, 且 lim εk = 0. 若存在一个有界常数 k=∞ 0 < c < ∞, 使得 |εk+1 | lim = c, k→∞ |εk |p 则称点列 {εk } 是 p 次 (渐进) 收敛的. 若 1 < p < 2 或 p = 1 且 c = 0, 则 称点列是超线性收敛的. 10/67 

11 .2 矩阵与投影 2.1 特征值与特征向量 2.2 对称正定矩阵 2.3 投影变换与投影矩阵 2.4 不变子空间 11/67 

12 .2.1 特征值与特征向量 定义 7 设 A ∈ Cn×n , 称 pA (λ) = det(A − λI) 为 A 的特征多项式, 其零 点就是 A 的特征值. 定理 9 (Cayley-Hamilton) [135] 设 pA (λ) 是 A ∈ Cn×n 的特征多项式, 则 pA (A) = 0. 由 Cayley-Hamilton 定理可知, 总存在一个多项式 p(t) 使得 p(A) = 0. 我 们称满足 p(A) = 0 的首项系数为 1 的次数最低的多项式为 A 的最小多 项式. 最小多项式可以通过 Jordan 标准型来计算, 见定理 29. 定义 8 设 A ∈ Cn×n . 若存在 λ ∈ C 和非零向量 x, y ∈ Cn , 满足 Ax = λx, y ∗ A = λy ∗ , 则称 λ 为 A 的特征值, x 为 A 对应于 λ 的（右）特征向量, y 为 A 对应 于 λ 的左特征向量, 并称 (λ, x) 为 A 的一个特征对 (eigenpair). 关于特征值的几个说明: • 只有当 A 是方阵时, 才具有特征值与特征向量; • 实矩阵的特征值与特征向量有可能是复的; • n 阶矩阵总是存在 n 个特征值（其中可能有相等的）; • 特征值有代数重数和几何重数; • 相似变换不改变矩阵的特征值; • 矩阵 A 的所有特征值组成的集合称为 A 的谱, 通常记为 σ(A). 定义 9 设 A ∈ Rn×n . 若存在一个非奇异矩阵 X ∈ Cn×n , 使得 X −1 AX = Λ, (1.2) 其中 Λ ∈ Cn×n 是对角矩阵. 则称 A 是可对角化的, 矩阵 Λ 的对角线元 12/67 

13 .素即为 A 的特征值, 分解 (1.2) 称为矩阵 A 的特征值分解或谱分解. 定理 10 设 A ∈ Cn×n . 则 (1) A 可对角化当且仅当 A 有 n 个线性无关的特征向量; (2) A 可对角化当且仅当 A 的所有特征值的代数重数与几何重数都 相等; (3) 若 A 有 n 个互不相等的特征值, 则 A 可对角化. 1 1 定理 11 (Bendixson) 设 A ∈ Cn×n , 令 H = (A + A∗ ), S = (A − A∗ ). 2 2 则有 λmin (H) ≤ Re(λ(A)) ≤ λmax (H), λmin (iS) ≤ Im(λ(A)) ≤ λmax (iS), 其中 Re(·) 和 Im(·) 分别表示实部和虚部. 这个定理告诉我们, 一个矩阵的特征值的实部的取值范围由其 Hermite 部 分确定, 而虚部则由其反 Hermite 部分确定. 定理 12 矩阵的特征值关于矩阵元素是连续的. 即当矩阵的元素发生变 化时, 其特征值的变化是连续的. 该结论可以通过多项式零点关于多项式系数的连续性得到. 13/67 

14 .2.2 对称正定矩阵 定义 10 设 A ∈ Cn×n . • 若对所有向量 x ∈ Cn 有 Re(x∗ Ax) ≥ 0, 则称 A 是半正定的; 进一 步, 若对所有非零向量 x ∈ Cn 有 Re(x∗ Ax) > 0, 则称 A 是正定的. • 若 A 是 Hermite 的且半正定, 则称 A 为 Hermite 半正定; • 若 A 是 Hermite 的且正定, 则称 A 为 Hermite 正定; † 若对所有向量 x ∈ Cn 有 x∗ Ax ∈ R, 则 A∗ = A. 因此, 若 A 是 Hermite (半) 正定的, 则 A 必定是 Hermite 矩阵. † 正定和半正定矩阵不一定对称或 Hermite . 定理 13 设 A ∈ Cn×n . 则 A 正定 (半正定) 的充要条件是矩阵 H = 1 (A + A∗ ) 正定 (半正定). 2 定理 14 设 A ∈ Rn×n . 则 A 正定 (半正定) 的充要条件是对任意非零向 量 x ∈ Rn 有 x Ax > 0 (x Ax ≥ 0). 如果 A 是 Hermite (半) 正定矩阵, 则可以定义其平方根, 即存在唯一的 Hermite (半) 正定矩阵 B, 使得 B 2 = A. 事实上, 我们有下面更一般的性 质. 定理 15 设 A ∈ Cn×n 是一个 Hermite 半正定矩阵, k 是一个给定的正 整数. 则存在一个唯一的 Hermite 半正定矩阵 B ∈ Cn×n 使得 B k = A. 同时, 我们还有下面的性质: (1) BA = AB, 且存在一个多项式 p(t) 使得 B = p(A); 14/67 

15 . (2) rank(B) = rank(A), 因此, 若 A 是正定的, 则 B 也正定; (3) 如果 A 是实矩阵的, 则 B 也是实矩阵. 证明. 可参见 [135]. 1 特别地, 当 k = 2 时, 称 B 为 A 的平方根, 通常记为 A 2 . 15/67 

16 .2.3 投影变换与投影矩阵 设 S1 和 S2 是内积空间 S 的两个子空间, 且 S = S1 ⊕ S2 , 则 S 中的任意 向量 x 都可唯一表示为 x = x1 + x2 , x1 ∈ S1 , x2 ∈ S2 . 我们称 x1 为 x 沿 S2 到 S1 上的 投影, 记为 x|S1 . 设线性变换 P : S → S. 如果对任意 x ∈ S, 都有 P x = x|S1 , 则称 P 是从 S 沿子空间 S2 到子空间 S1 上的 投影变换 (也称 投影算子 或 投影矩阵), 对应的变换矩阵称为 投影矩阵. † 线性变换在不同的基下对应不同的变换矩阵. 在不加特别指出时, 本讲义中如果线性空间是 Rn 或 Rm×n , 我们采用单位标准基, 如 {e1 , e2 , . . . , en } . 设 P 是从 S 沿子空间 S2 到子空间 S1 上的投影变换, 则对任意 x ∈ S1 都 有 P x = x. 因此, S1 ⊆ Ran(P ). 又由定义可知 Ran(P ) ⊆ S1 , 所以 S1 = Ran(P ). 类似地, 我们也可以验证 S2 = Ker(P ). 于是存在直和分解 S = Ran(P ) ⊕ Ker(P ). 若 S = Rn , 则立即可以得到下面的结论. 引理 4 设 P ∈ Rn×n 是一个投影矩阵, 则 Rn = Ran(P ) ⊕ Ker(P ). (1.3) 反之, 若 (1.3) 成立, 则 P 是沿子空间 Ker(P ) 到子空间 Ran(P ) 上的投影 16/67 

17 .变换. 下面的性质说明, 投影矩阵由其像空间和零空间唯一确定. 引理 5 若 S1 和 S2 是 Rn 的两个子空间, 且 Rn = S1 ⊕ S2 , 则存在唯一 的投影矩阵 P , 使得 Ran(P ) = S1 , Ker(P ) = S2 , 即对任意向量 x ∈ Rn , 有 P x ∈ S1 , x − P x ∈ S2 . 下面给出一个投影矩阵的判别定理. 定理 16 矩阵 P ∈ Rn×n 是投影矩阵的充要条件是 P 2 = P , 即 P 是幂 等矩阵 (Idempotence ). 证明. 必要性: 设 P 是投影矩阵, 则对任意 x ∈ Rn , 都有 P 2 x = P (P x) = P x. 因此 P 2 = P . 充分性: 设 P 2 = P . 我们只需证明 Ran(P ) + Ker(P ) = Rn . 显然 Ran(P ) + Ker(P ) ⊆ Rn , 因此只要证明 Rn ⊆ Ran(P ) + Ker(P ). 对任意 x ∈ Rn , 有 x = P x + (x − P x). 由 P (x − P x) = P x − P 2 x = 0 可知 x − P x ∈ Ker(P ). 因此 Rn ⊆ Ran(P ) + Ker(P ). 所以结论 Ran(P ) + Ker(P ) = Rn 成立. 引理 6 设 P ∈ Rn×n 是一个投影矩阵, 则 (1) I − P 也是一个投影矩阵, 且 Ker(P ) = Ran(I − P ); (2) P 也是一个投影矩阵. 设 S1 和 S2 是 Rn 的两个 m 维子空间. 如果 S1 ∩ S2⊥ = {0} (或 Rn = 17/67 

18 .S1 ⊕ S2⊥ ), 则存在唯一的投影矩阵 P , 使得 Ran(P ) = S1 , Ker(P ) = S2⊥ . 此 时, 我 们 称 P 是 S1 上 与 S2 正 交的 投 影 矩 阵. 令 v1 , v2 , . . . , vm 和 w1 , w2 , . . . , wm 分别是 S1 和 S2 的一组基, 则 P 可以由这两组基来表 示. 定理 17 设 P ∈ Rn×n 是 S1 上与 S2 正交的投影矩阵, 则 P = V (W V )−1 W , (1.4) 其中 V = [v1 , v2 , . . . , vm ], W = [w1 , w2 , . . . , wm ]. † 虽然投影矩阵 P 由子空间 S1 和 S2 唯一确定, 但其矩阵表示形式 (1.4) 并不唯一. 定理 18 (正交投影) 设 S1 是内积空间 S 的一个子空间, x ∈ S, 则 x 可 唯一分解成 x = x1 + x2 , x1 ∈ S1 , x2 ∈ S1⊥ , 其中 x1 称为 x 在 S1 上的正交投影. 若 P 是从 S 沿子空间 S1⊥ 到子空间 S1 上的投影变换, 则称 P 为子空间 S1 上的 正交投影变换 (也称 正交投影算子, 对应的矩阵称为 正交投影矩 阵), 记为 PS1 . 如果 P 不是正交投影变换, 则称其为斜投影变换 (oblique projector ) 定理 19 投影矩阵 P ∈ Rn×n 是正交投影矩阵的充要条件 P = P . 由定理 17 可立即得到下面的结论. 18/67 

19 .推论 20 设 P 是子空间 S1 上的 正交投影变换. 令 v1 , v2 , . . . , vm 是 S1 的一组标准正交基, 则 P =VV . 正交投影的一个基本性质是 定理 21 设 P ∈ Rn×n 是一个正交投影矩阵, 则 ∥P ∥2 = 1, 且对 ∀ x ∈ Rn , 有 ∥x∥22 = ∥P x∥22 + ∥(I − P )x∥22 . 下面是关于正交投影的一个很重要的应用. 定理 22 设 S1 是 Rn 的一个子空间, z ∈ Rn 是一个向量. 则最佳逼近问 题 min ∥x − z∥2 x∈S1 的唯一解为 x∗ = PS1 z. 即 S1 中距离 z 最近 (2-范数意义下) 的向量是 z 在 S1 上的正交投影. 上述结论可推广到一般能量范数情形. 推论 23 设 A ∈ Rn×n 对称正定, S1 是 Rn 的一个子空间, 向量 x∗ ∈ S1 ⊆ Rn . 则 x∗ 是最佳逼近问题 min ∥x − z∥A x∈S1 的解的充要条件是 A(x∗ − z) ⊥ S1 . 19/67 

20 . 1 这里 ∥x − z∥A ∥A 2 (x − z)∥2 . 20/67 

21 .2.4 不变子空间 定义 11 设 A ∈ Rn×n , 子空间 S ⊆ Rn . 若 AS ⊆ S, 即对任意 x ∈ S, 都 有 Ax ∈ S, 则称 S 为 A 的一个不变子空间. 由特征向量张成的子空间是不变子空间. 定理 24 设 x1 , x2 , . . . , xm 是 A 的一组线性无关的特征向量, 则 span{x1 , x2 , . 是 A 的一个 m 维不变子空间. 定理 25 设 A ∈ Rn×n , X ∈ Rn×k 且 rank(X) = k. 则 span(X) 是 A 的 不变子空间的充要条件是存在一个矩阵 B ∈ Rk×k 使得 AX = XB, 此时, B 的特征值都是 A 的特征值. 证明. 可参见《矩阵计算讲义》[272]. 推论 26 设 A ∈ Rn×n , X ∈ Rn×k 且 rank(X) = k. 若存在一个矩阵 B ∈ Rk×k 使得 AX = XB, 则 (λ, v) 是 B 的一个特征对当且仅当 (λ, Xv) 是 A 的一个特征对. 21/67 

22 .3 矩阵标准型 3.1 Jordan 标准型 3.2 Schur 标准型 22/67 

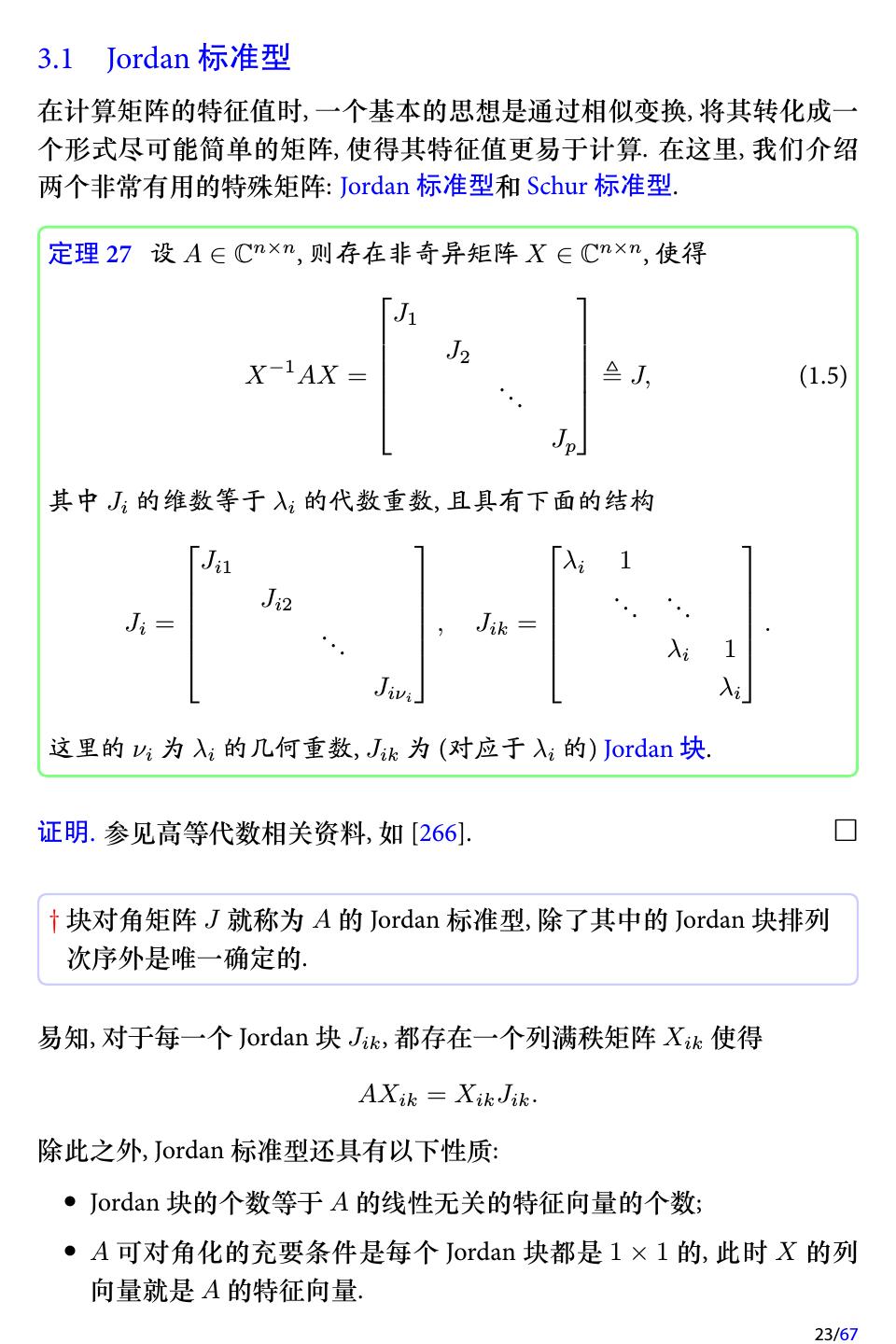
23 .3.1 Jordan 标准型 在计算矩阵的特征值时, 一个基本的思想是通过相似变换, 将其转化成一 个形式尽可能简单的矩阵, 使得其特征值更易于计算. 在这里, 我们介绍 两个非常有用的特殊矩阵: Jordan 标准型和 Schur 标准型. 定理 27 设 A ∈ Cn×n , 则存在非奇异矩阵 X ∈ Cn×n , 使得   J1    J2  −1 X AX =    J, (1.5) ..   .  Jp 其中 Ji 的维数等于 λi 的代数重数, 且具有下面的结构     Ji1 λi 1    .. ..   Ji2   . .  Ji =   ..  , Jik =    .   .   λi 1 Jiνi λi 这里的 νi 为 λi 的几何重数, Jik 为 (对应于 λi 的) Jordan 块. 证明. 参见高等代数相关资料, 如 [266]. † 块对角矩阵 J 就称为 A 的 Jordan 标准型, 除了其中的 Jordan 块排列 次序外是唯一确定的. 易知, 对于每一个 Jordan 块 Jik , 都存在一个列满秩矩阵 Xik 使得 AXik = Xik Jik . 除此之外, Jordan 标准型还具有以下性质: • Jordan 块的个数等于 A 的线性无关的特征向量的个数; • A 可对角化的充要条件是每个 Jordan 块都是 1 × 1 的, 此时 X 的列 向量就是 A 的特征向量. 23/67 

24 .推论 28 所有可对角化矩阵组成的集合在所有矩阵组成的集合中是稠 密的. 可通过矩阵的 Jordan 标准型来计算最小多项式. 定理 29 设 λ1 , λ2 , . . . , λp 为 A ∈ Cn×n 的互不相等的特征值, 则 A 的最 小多项式为 ∏ p qA (t) = (t − λi )ri , i=1 其中 ri 是 λi 的最大 Jordan 块的维数. 24/67 

25 .3.2 Schur 标准型 Jordan 标准型在理论研究中非常有用, 但数值计算比较困难, 目前还没有 找到十分稳定有效的数值算法. 下面我们介绍一个比较实用的标准型: Schur 标准型. 定理 30 设 A ∈ Cn×n , 则存在一个酉矩阵 U ∈ Cn×n 使得   λ1 r12 · · · r1n    0 λ2 · · · r2n  ∗  ..  ∗ U AU =  . . ..  R 或 A = U RU , (1.6)  . . .  0 · · · 0 λn 其中 λ1 , λ2 , . . . , λn 是 A 的特征值 (可以按任意顺序排列). 证明. 可参见《矩阵计算讲义》[272]. 关于 Schur 标准型的几点说明: • Schur 标准型可以说是酉相似变化下的最简形式; • 定理中的 U 和 R 不是唯一的, 其中 R 的对角线元素可以按任意顺序 排列. 推论 31 设 A ∈ Cn×n , 则 • A 是正规矩阵当且仅当 (1.6) 中的 R 是对角矩阵, 即 A 可酉对角化 当且仅当 A 是正规矩阵; • A 是 Hermite 矩阵当且仅当 (1.6) 中的 R 是实对角矩阵. 众所周知, 当 A 是实矩阵时, 其特征值和特征向量仍可能是复的. 在实 际计算中, 我们希望避免复数运算. 下面我们给出实 Schur 标准型 (或拟 Schur 标准型). 25/67 

26 .定理 32 设 A ∈ Rn×n , 则存在正交矩阵 Q ∈ Rn×n , 使得 Q AQ = T, (1.7) 其中 T ∈ Rn×n 是 拟上三角矩阵, 即 T 是块上三角的, 且对角块为 1 × 1 或 2 × 2 的块矩阵. 若对角块是 1 × 1 的, 则其就是 A 的一个特征值, 若 对角块是 2 × 2 的, 则其特征值是 A 的一对共轭复特征值. 证明. 可参见《矩阵计算讲义》[272]. 易知, 若 A 的实 Schur 标准型 T 是对角矩阵, 则 A 的特征值都是实的. 反 之, 结论也成立. 推论 33 设 A ∈ Rn×n 的特征值都是实的, 则存在正交矩阵 Q ∈ Rn×n 和上三角矩阵 R ∈ Rn×n 使得 Q AQ = R, 其中 R 的对角线元素即为 A 的特征值. ¶ 若 A 是实正规矩阵, 则其 Schur 分解中的 U 和 R 是否也都可以是实 的? 26/67 

27 .4 数值域 4.1 基本概念与性质 4.2 数值域的凸性 4.3 矩阵乘积的数值域 27/67 

28 .4.1 基本概念与性质 设 A ∈ Cn×n , 非零向量 x ∈ Cn . 则 A 关于 x 的 Rayleigh 商 (Rayleigh Quotient) 定义为 x∗ Ax q(x) . x∗ x 易知, q(·) 是 Cn 上的零次齐次函数, 即 q(αx) = q(x), ∀ α ∈ C, α ̸= 0. 定义 12 设 A ∈ Cn×n . 则 A 的数值域 (Numerical Range, Field of Values) 定义为 F(A) {x∗ Ax : x ∈ Cn , x∗ x = 1}, 相应地, A 的 数值域半径 (Numerical Radius) 定义为 r(A) max{|µ| : µ ∈ F (A)}. 显然数值域是 C 中的一个连续集合. 数值域可以用来研究矩阵的性质, 如 特征值分布, 范数估计, 谱半径估计等. 有时能提供一些特征值无法提供 的信息. 28/67 

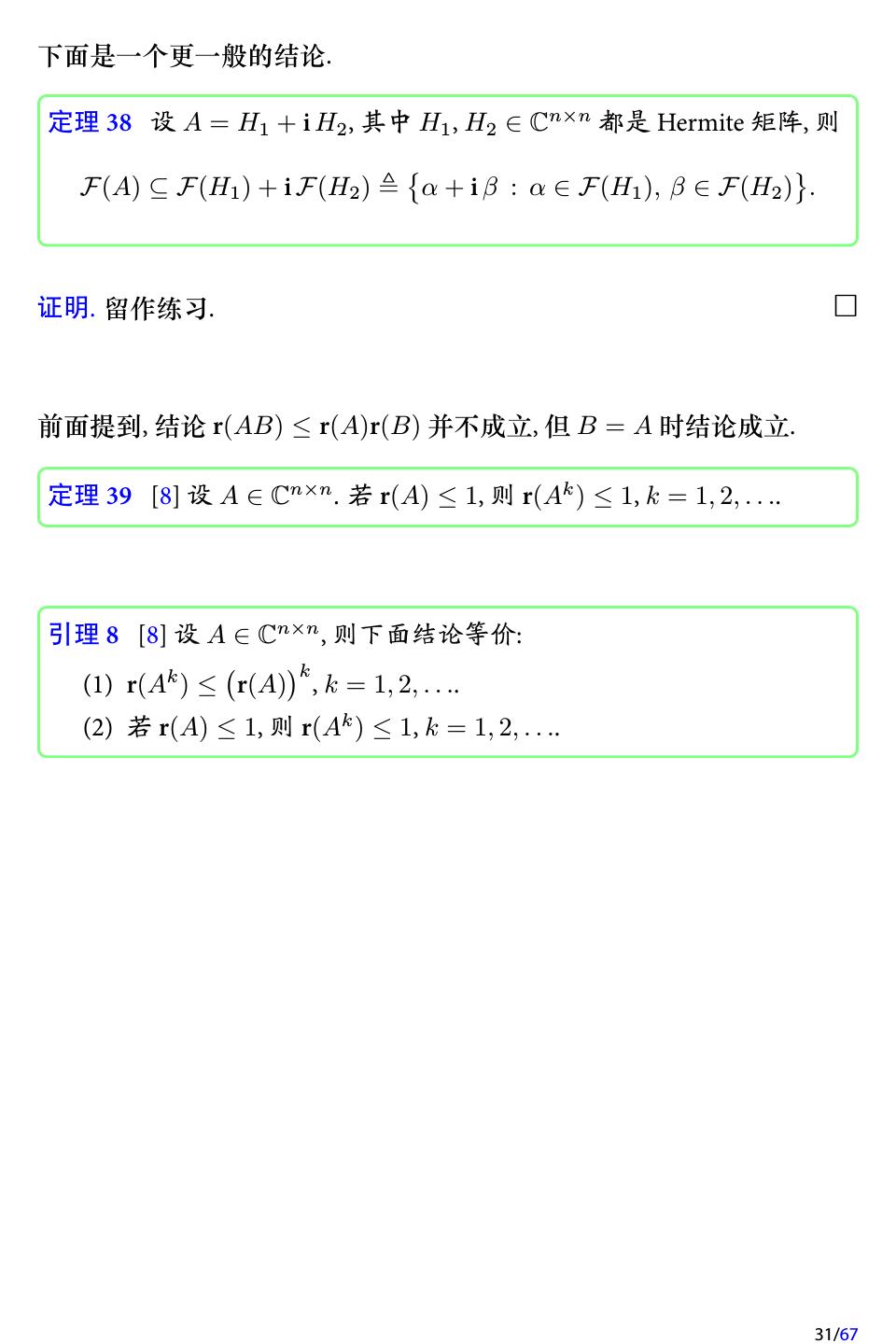
29 .我们记矩阵的谱为 σ(A), 即 σ(A) {λ1 , λ2 , . . . , λn }, 其中 λi 是 A 的特征值. 易知 σ(A) 是一个离散的点集. 下面给出数值域与数值域半径的一些基本性质 [8, 118, 127, 136]. 引理 7 设 A ∈ Cn×n , 则下面结论成立. (1) σ(A) ⊆ F (A); (2) F(A + αI) = F(A) + α, ∀ α ∈ C; (3) F(αA) = αF(A), ∀ α ∈ C; (4) F(A ) = F(A), F(A∗ ) = F(A); (5) 设 U 是酉矩阵, 则 F(U AU ∗ ) = F(A), 即数值域在酉相似变换下 是不变的; (6) 设 X ∈ Cn×k 是列正交的, 即 X ∗ X = I, 其中 k ≤ n, 则 F(X ∗ AX) ⊆ F(A), 特别地, 对任意主子矩阵 Ak , 都有 F(Ak ) ⊆ F (A); (7) 若 A 是正规矩阵, 则 F(A) = F(diag(λ1 , λ2 , . . . , λn )), 其中 λi (1 ≤ i ≤ n) 是 A 的特征值; (8) F(A) 是线段 (射线, 或直线) 当且仅当存在常数 α, β ∈ C (α ̸= 0) 使得 αA + βI 是 Hermite 的, 特别地 • F(A) = {α} ⇐⇒ A = αI, • F(A) ⊆ R ⇐⇒ A 是 Hermite, • F(A) ⊆ (0, ∞) ⇐⇒ A 是 Hermite 正定, • F(A) ⊆ [0, ∞) ⇐⇒ A 是 Hermite 半正定. 证明. 直接验证即可, 留作练习. 29/67