展开查看详情
1 .1 数 值 分 析 Numerical Analysis 潘建瑜 华东师范大学数学系
2 .科学计算 计算机 硬件 软件： 核心是算法 数值算法 非数值算法 计算机硬件所追求的是快而稳定 软件则是利用计算机高速的简单运算去 实现各种复杂 的功能 和 解决 各种复杂的问题 2
3 .科学计算 3 借助计算机高速计算的能力，解决现代科学、工程、经济或人文中的复杂问题，是计算机与数学的有机结合 科学计算 是 20 世纪重要科学技术进步之一 ，已 与 理论研究 和 实验研究 相并列成为 科学研究的第三种 方法 。 现今 科学计算已是体现国家科学技术核心竞争力的重要标志，是国家科学技术创新发展的关键 要素 。 —— 国家自然科学基金委员会， 2014 年重大研究计划项目指南 在 迅猛发展的高性能计算技术推动下 , 计算科学 将 是 21 世纪确保国家核心竞争能力的战略技术之一 。 —— 计算 科学 : 确保美国 竞争力， 2005 年美国总统信息技术咨询 委员会
4 .科学计算 4 科学计算的 核心 / 数学基础： 计算 数学 传统的科学计算 是 针对科学和工程中的 数学问题， 设计 / 分析有效的求解算法， 即 为 数值分析 / 计算方法
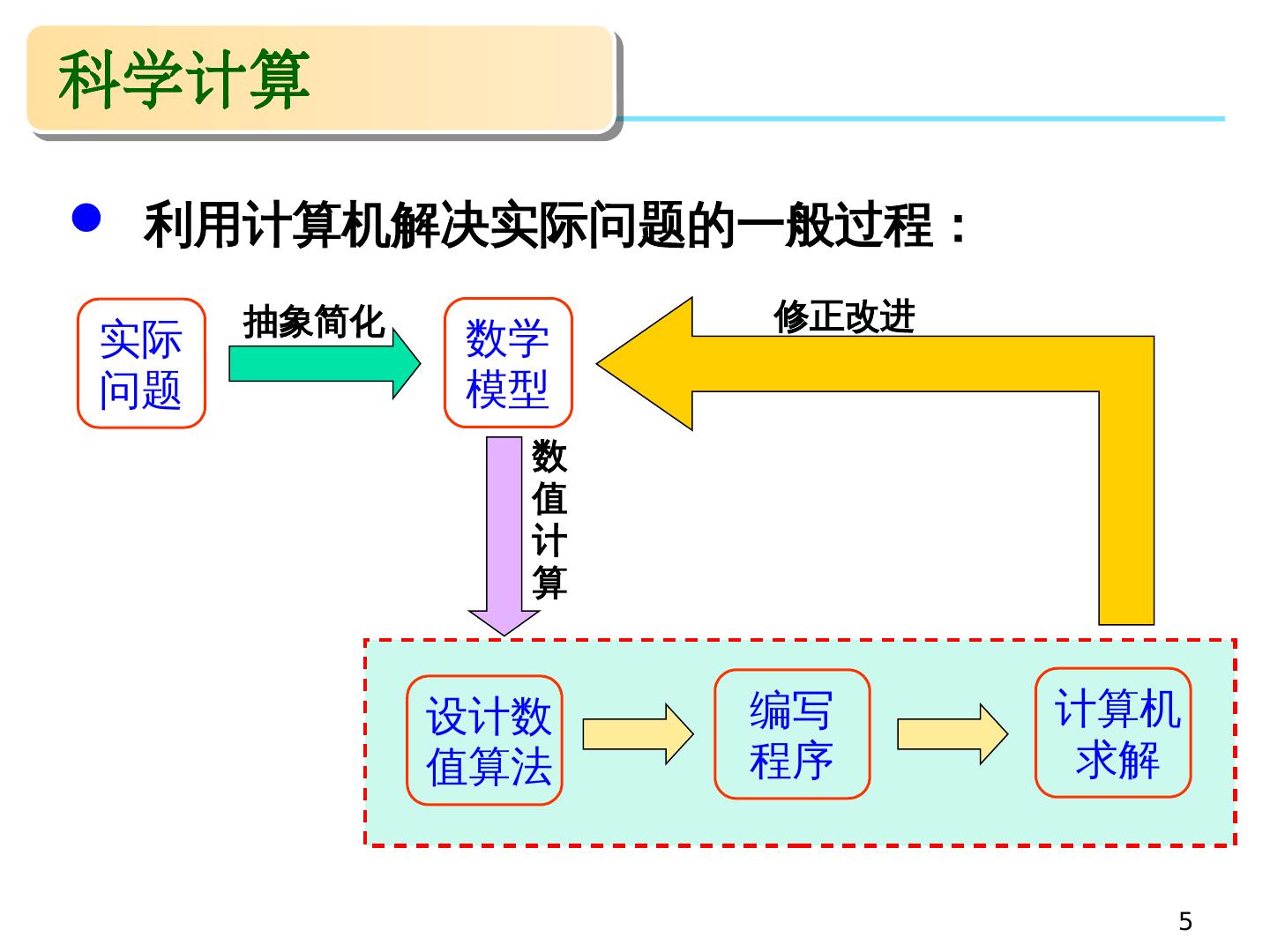
5 .科学计算 5 利用计算机解决实际问题的一般过程： 抽象简化 数 值 计 算 修正改进 实际 问题 数学 模型 设计数 值算法 编写 程序 计算机 求解
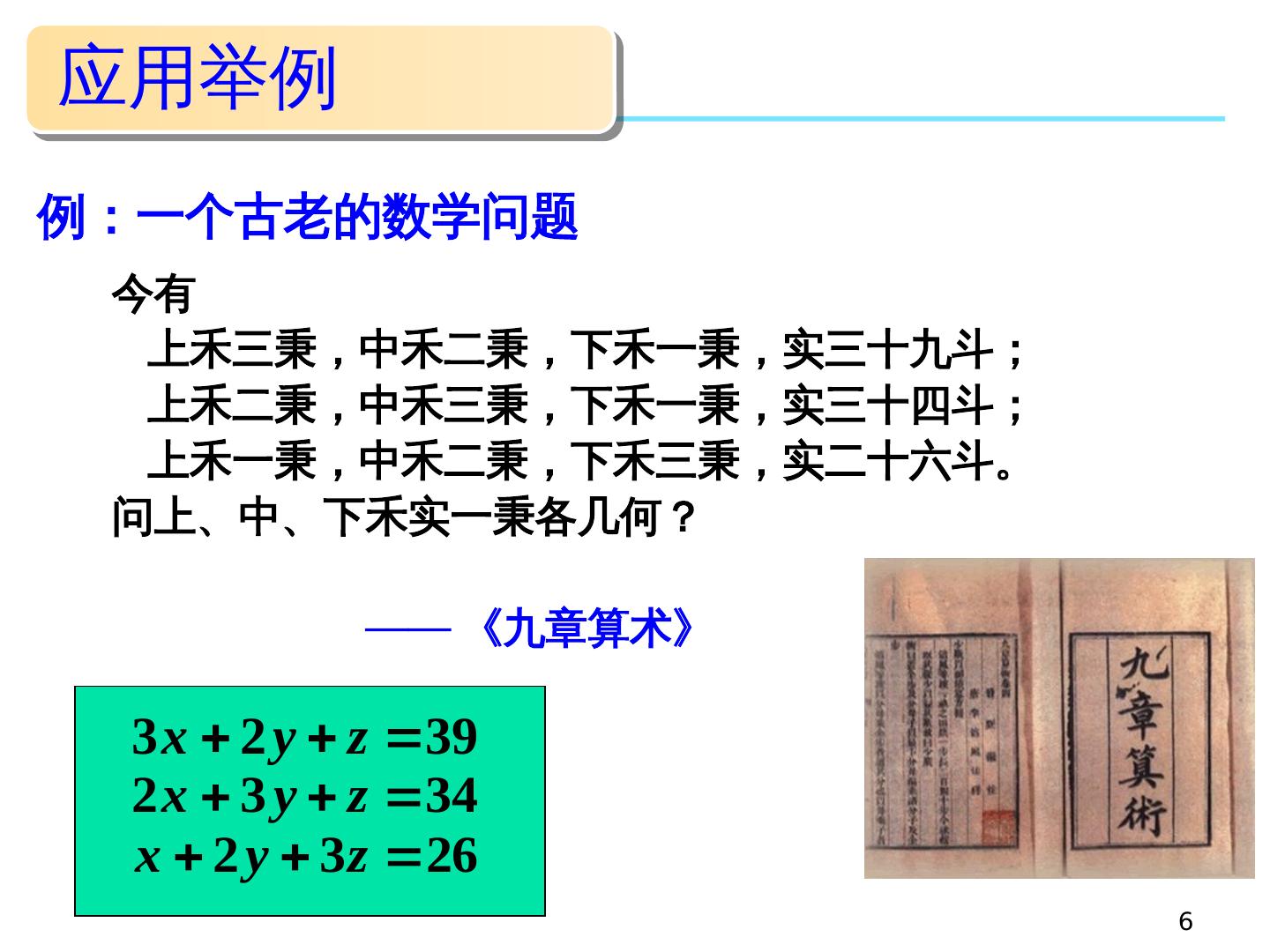
6 .应用举例 6 今 有 上禾三秉，中禾二秉，下禾一秉，实三十九斗； 上禾二秉，中禾三秉，下禾一秉，实三十四斗； 上禾一秉，中禾二秉，下禾三秉，实二十六斗。 问上、中、下禾实一秉各几何？ —— 《 九章算术 》 例：一个古老的数学问题
7 .应用举例 7 线性方程组 数值 求解 —— 教材第五、 六 章
8 .应用举例 8 非线性方程数值解法 —— 教材 第七章 例： 怎样计算平方根？如
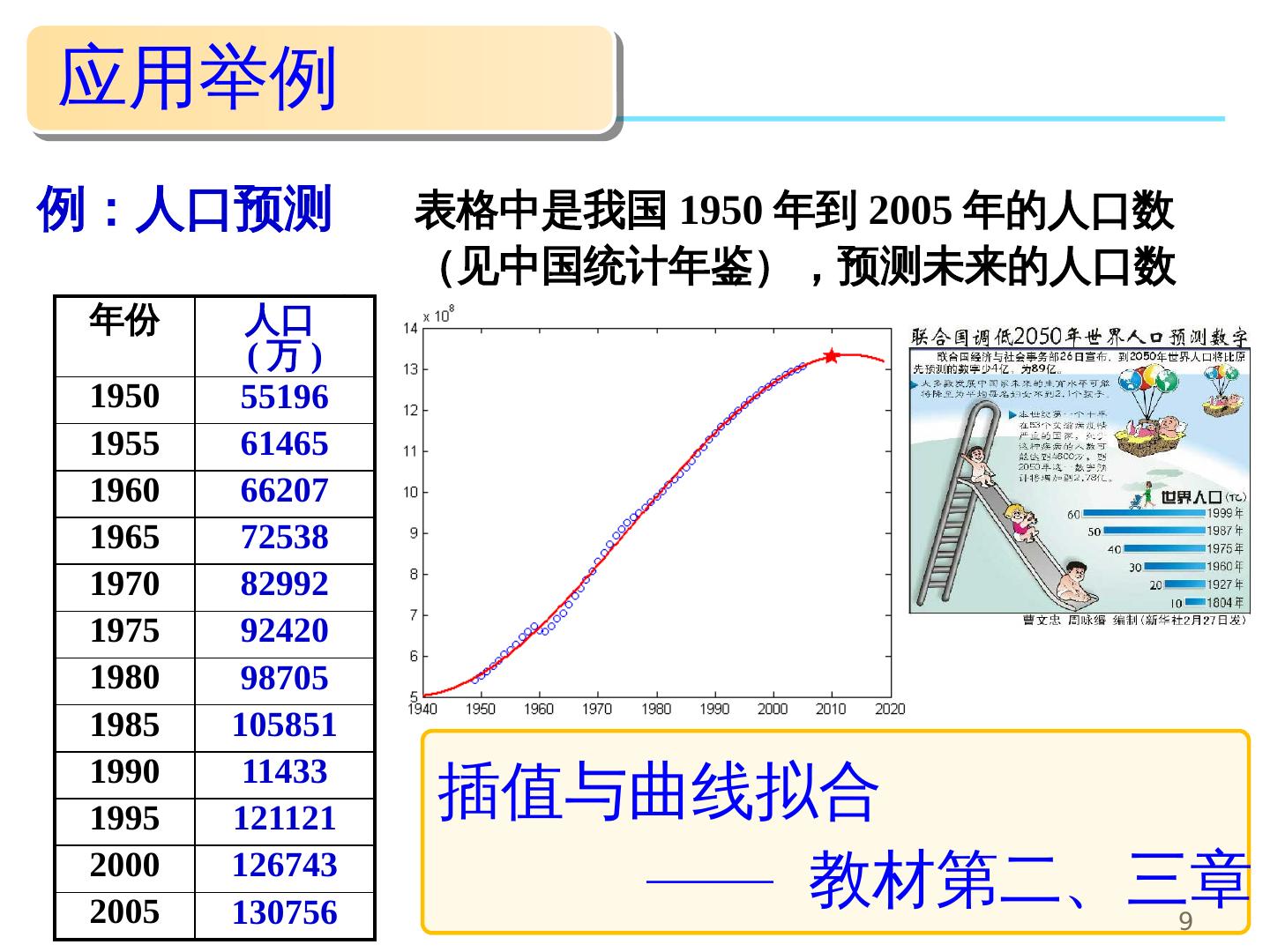
9 .应用举例 9 例：人口预测 表格中是我国 1950 年到 2005 年的人口 数 （ 见中国统计年鉴 ），预测 未来的人口数 年份 人口 ( 万 ) 1950 55196 1955 61465 1960 66207 1965 72538 1970 82992 1975 92420 1980 98705 1985 105851 1990 11433 1995 121121 2000 126743 2005 130756 插值 与 曲线拟合 —— 教材第二、三章
10 .应用举例 10 例：G oogle 搜索引擎 1998 年创立， 市值 8151 亿 ( 2018.01.28) G : Google Matrix, “the world’s largest matrix computation” x : PageRank vector “ The $25,000,000,000 Eigenvector” —— SIAM Review ， 2006 G x = x , e T x =1 矩阵特征值计算 —— 教材第八 章
11 .数值分析 11 数值分析 / 计算方法的任务 设计求解各种实际问题的 高效可靠 的数值方法 可靠 ：收敛性稳定性等有数学理论保证 高效：尽可能地节省计算时间和 存储空间 对求得的 数值 解的精度进行评估 研究数值算法 在计算机上 的 实现 对于同一个问题，不同的算法在计算 性能上可能相差百万倍或者更多！
12 .数值分析 12 例： 求解一个 n 阶线性方程组 ，若使用 克莱姆法则 ，需要计算 n +1 个 n 阶行列式，在不计加减运算情况下 ，需要 n !( n 2 -1) 次乘除运算。而使用高斯消去法，只需 约 2 n 3 /3 次乘除 运算。 用每秒运算 30 亿次（主频 3.0G） 的计算机求解时，大约需要10000年的时间 当 n =20 时， 如果使用高斯消去法，不到一秒钟就能完成！
13 .数值方法 13 数值方法的特点 方法是近似的 ，所以求出的解是有误差的 与计算机紧密结合 ：易于上机 实现 熟悉一门语言： C 语言或 Fortran 语言 掌握一种数学软件： Matlab ， Maple 或 Mathematica Matlab 优点： 用 Matlab 处理矩阵 —— 容易 用 Matlab 绘图 —— 轻松 用 Matlab 编程 —— 简洁 用 Matlab 的工具箱 —— 高效
14 .几个基本概念 14 解析解、精确解、真解、真值 数值解、近似解 数值方法 / 算法：求问题的数值解的方法 算法的可靠性包括：收敛性，稳定性，误差估计等 算法的评价（优劣） 时间复杂度 （计算机运行时间） 空间复杂度 （所占用的计算机存储空间） 逻辑复杂度 （影响程序开发的周期以及维护的难易程度）
15 .课程基本信息 15 教材 ： 电子讲义 + 数值分析 （第五 版 , 李 庆扬 等 , 2008 ） 上机 ： 第十一周开始 课程主页 ： http ://math.ecnu.edu.cn/~jypan/Teaching / 参考资料： 见课程主页 考核方式 ： 平时 40% （期 中 , 作业 , 上机 , 考勤） + 期末 60% 答疑 ： 周三晚 19:00—21:00 ，数学楼 229
16 .课程内容 16 函数插值 函数逼近 数值积分和数值微分 线性方程组的直接解法和迭代解法 非线性方程（组）的数值求解 矩阵特征值与特征向量的计算 常微分方程的数值解法
17 .预备知识 17 数学分析 高等 代数（线性代数） 常微分方程 Matlab 编程
18 .学习建议 18 注意掌握数值方法的基本 思想和原理 注意数值方法处理 的 常用技巧 注重必要的数值 计算训练 （手算能力，编程能力） 要重视 误差分析 、 收敛性 和 稳定性 的基本 理论
热门城市
