- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
05_对称特征值
展开查看详情
1 .第五讲 对称特征值问题 1 Jacobi 迭代 2 Rayleigh 商迭代 3 对称 QR 迭代 4 分而治之法 5 对分法和逆迭代 6 奇异值分解 7 扰动分析
2 .关于对称特征值问题的常用算法有 (直接法): • Jacobi 迭代: 最古老, 收敛速度较慢, 但精度较高, 且很适合并行计算. • Rayleigh 商迭代: 一般具有三次收敛性, 但需要解方程组. • 对称 QR 迭代: 对称矩阵的 QR 方法. 对于对称三对角矩阵, 若只计算 特征值, 则速度最快 (运算量为 O(n2 )). 如果还需要计算特征向量, 则 运算量约为 6n3 . • 分而治之法 (Divide-and-Conquer) : 同时计算特征值和特征向量的一 种快速算法. 基本思想是将大矩阵分解成小矩阵, 然后利用递归思想 求特征值. 在最坏的情形下, 运算量为 O(n3 ). 在实际应用中, 平均为 O(n2.3 ). 如果使用快速多极子算法 (FMM) 后, 理论上的运算量可降 低到 O(n logp n), 其中 p 是一个较小的整数, 这使得分而治之算法成 为目前计算对称三对角矩阵的特征值和特征向量的首选方法. 2/102
3 .• 对分法和反迭代: 对分法主要用于求解对称三对角矩阵在某个区间 中的特征值, 运算量约为 O(kn), 其中 k 为所需计算的特征值的个数. 反迭代用于计算特征向量, 在最佳情况下, 即特征值 “适当分离” 时, 运算量约为 O(kn), 但在最差情况下, 即特征值成串地紧靠在一起时, 运算量约为 O(k 2 n), 而且不能保证特征向量的精度 (虽然实际上它 几乎是精确的). † 除了 Jacobi 迭代和 Rayleigh 商迭代外, 其余算法都需要先将对称矩 4 阵三对角化, 这个过程大约需花费 n3 的工作量, 如果需要计算特征 3 8 3 向量的话, 则运算量约为 n . 3 3/102
4 .1 Jacobi 迭代 基本思想: 通过一系列的 Jacobi 旋转 将 A 正交相似于一个对角矩阵: A(0) = A, A(k+1) = JkT A(k) Jk , k = 0, 1, . . . , 且 A(k) 收敛到一个对角矩阵, 其中 Jk 为 Jacobi 旋转, 即 Givens 变换: ik jk I cos θk · · · − sin θk ik Jk = G(ik , jk , θk ) = .. .. .. . . . jk sin θk · · · cos θk I 4/102
5 .引理 设 A ∈ R2×2 是对称矩阵, 则存在 Givens 变换 G ∈ R2×2 使得 GT AG 为对角阵. (板书) 5/102
6 .为了使得 A(k) 收敛到一个对角矩阵, 其非对角元素必须趋向于 0. 记 off(A) 为所有非对角元素的平方和, 即 ∑ ∑ n off(A) = a2ij = ∥A∥2F − a2ii , i̸=j i=1 我们的目标就是使得 off(A) 尽快趋向于 0. 引理 设 A = [aij ]n×n ∈ Rn×n 是对称矩阵, Aˆ = [ˆ aij ]n×n = J T AJ, J = G(i, j, θ), 其中 θ 的选取使得 a ˆji = 0, 则 ˆij = a ˆ = off(A) − 2a2 . off(A) ij (板书) 6/102
7 .算法 1.1 Jacobi 迭代算法 1: Given a symmetric matrix A ∈ Rn×n 2: if eigenvectors are desired then 3: set J = I and shif t = 1 4: end if 5: while not converge do 6: choose an index pair (i, j) such that aij ̸= 0 7: τ = (aii − ajj )/(2aij ) √ 8: t = sign(τ )/(|τ | + 1 + τ 2 ) % 计算 tan θ √ 9: c = 1/ 1 + t2 , s = c · t % 计算 Givens 变换 10: A = G(i, j, θ)T AG(i, j, θ) % 实际计算时不需要做矩阵乘积 11: if shif t = 1 then 12: J = J · G(i, j, θ) 13: end if 14: end while
8 .aij 的选取问题 一种直观的选取方法就是使得 aij 为所有非对角元素中绝对值最大的一 个, 这就是经典 Jacobi 算法. 8/102
9 .算法 1.2 经典 Jacobi 迭代算法 1: Given a symmetric matrix A ∈ Rn×n 2: if eigenvectors are desired then 3: set J = I and shif t = 1 4: end if 5: while off(A)> tol do 6: choose (i, j) such that |aij | = maxk̸=l |akl | 7: τ = (aii − ajj )/(2aij ) √ 8: t = sign(τ )/(|τ | + 1 + τ 2 ) √ 9: c = 1/ 1 + t2 , s = c · t 10: A = G(i, j, θ)T AG(i, j, θ) 11: if shif t = 1 then 12: J = J · G(i, j, θ) 13: end if 14: end while
10 .可以证明, 经典 Jacobi 算法至少是线性收敛的. 定理 对于经典 Jacobi 算法 1.2, 有 ( ) 1 n(n − 1) off(A (k+1) )≤ 1− off(A(k) ), N= . N 2 故 k 步迭代后, 有 ( )k ( )k 1 1 off(A(k) ) ≤ 1− off(A(0) ) = 1− off(A). N N (板书) 10/102
11 .事实上, 经典 Jacobi 算法最终是二次局部收敛的. 定理 经典 Jacobi 算法 1.2 是 N 步局部二次收敛的, 即对足够大的 k, 有 ( ) ( ( )) off A(k+N ) = O off2 A(k) . 11/102
12 .经典 Jacobi 算法的每一步都要寻找绝对值最大的非对角元, 费时不实用. 改进: 逐行扫描, 这就是 循环 Jacobi 迭代方法 算法 1.3 循环 Jacobi 迭代算法 (逐行扫描) 1: Given a symmetric matrix A ∈ Rn×n 2: if eigenvectors are desired then 3: set J = I and shif t = 1 4: end if 5: while off(A)> tol do 6: for i = 1 to n − 1 do 7: for j = i + 1 to n do 8: if aij ̸= 0 then 9: τ = (aii − ajj )/(2aij ) √ 10: t = sign(τ )/(|τ | + 1 + τ 2 ) √ 11: c = 1/ 1 + t2 12/102
13 .12: s=c·t 13: A = G(i, j, θ)T AG(i, j, θ) 14: if shif t = 1 then 15: J = J · G(i, j, θ) 16: end if 17: end if 18: end for 19: end for 20: end while 循环 Jacobi 也具有局部二次收敛性 [65, page 270]. 13/102
14 .2 Rayleigh 商迭代 在反迭代方法中, 以 Rayleigh 商作为位移. 关于 Rayleigh 商迭代的收敛性, 我们有下面的结论. 定理 设 A ∈ Rn×n 对 称, 且 特 征 值 都 是 单 重 的. 则 当 误 差 足 够 小 时, Rayleigh 商迭代中每步迭代所得的正确数字的位数增至三倍, 即 Rayleigh 商迭代是局部三次收敛的. (板书) 关于 RQI 算法的全局收敛性, 可参见文献 [49]. 14/102
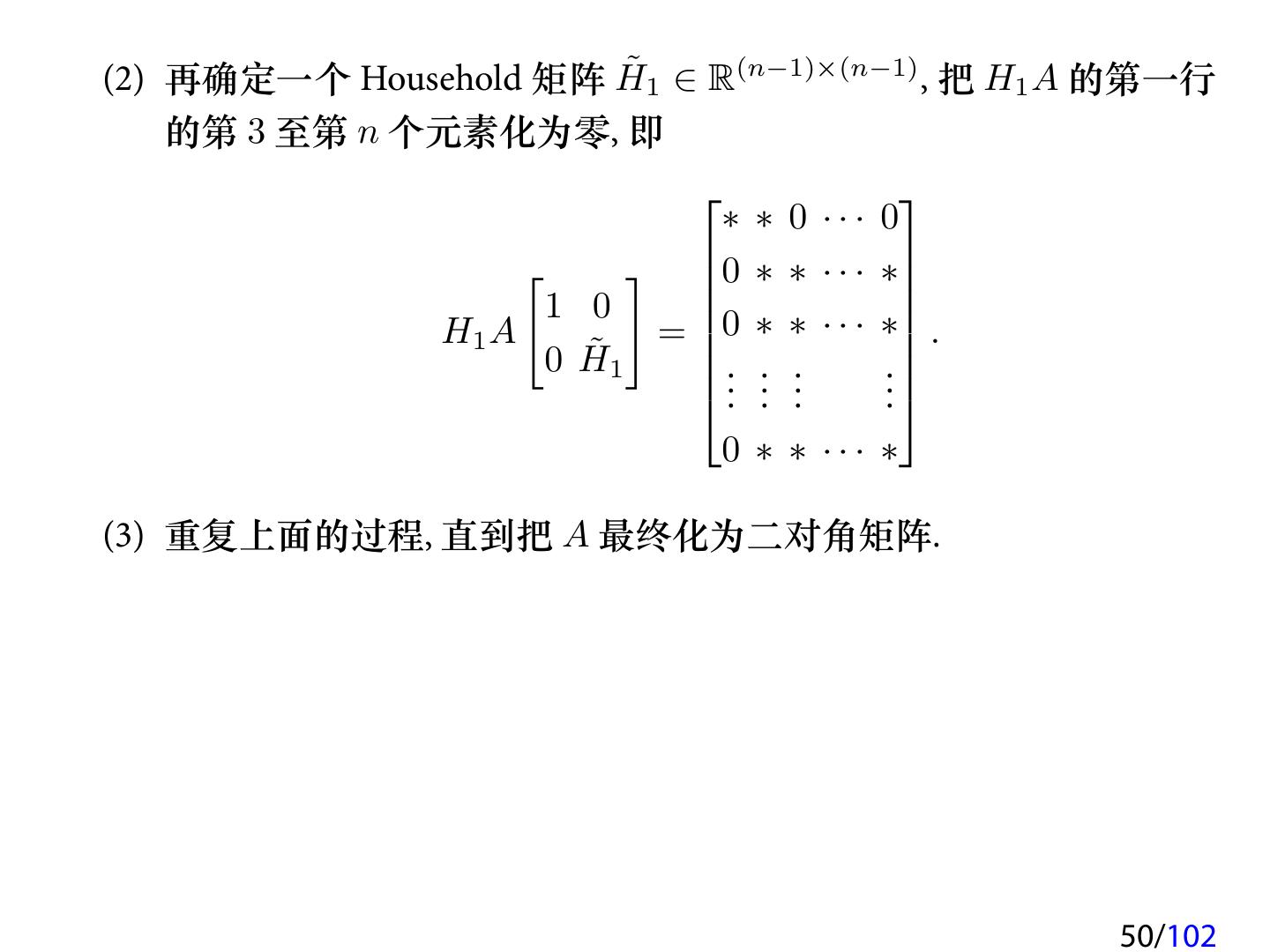
15 .3 对称 QR 迭代 将带位移的隐式 QR 方法运用到对称矩阵, 就得到对称 QR 迭代方法. 基本步骤 1. 对称三对角化: 利用 Householder 变换, 将 A 化为对称三对角矩阵, 即 计算正交矩阵 Q 使得 T = QAQT 为对称三对角矩阵; 2. 使用带 (单) 位移的隐式 QR 迭代算法计算 T 的特征值与特征值向量; 3. 计算 A 的特征向量. 15/102
16 . 对称三对角化 任何一个对称矩阵 A ∈ Rn×n 都可以通过正交变换转化成一个对称三对 角矩阵 T . 这个过程可以通过 Householder 变换来实现, 也可以通过 Givens 变换来实现. 对称 QR 迭代算法的运算量 • 三对角化 4n3 /3 + O(n2 ), 若需计算特征向量, 则为 8n3 /3 + O(n2 ); • 对 T 做带位移的隐式 QR 迭代, 每次迭代的运算量为 6n; • 计算特征值, 假定每个平均迭代 2 步, 则总运算量为 12n2 ; • 若要计算 T 的所有特征值和特征向量, 则运算量为 6n3 + O(n2 ); • 若只要计算 A 的所有特征值, 运算量为 4n3 /3 + O(n2 ); • 若计算 A 的所有特征值和特征向量, 则运算量为 26n3 /3 + O(n2 ); 16/102
17 . 位移的选取 — Wilkinson 位移 位移的好坏直接影响到算法的收敛速度. 我们可以通过下面的方式来选 取位移. 设 (k) (k) a1 b1 b(k) . . . . . . A(k) = 1 , .. .. . . b(k) n−1 (k) (k) bn−1 an (k) (k) 一种简单的位移选取策略就是令 σk = an . 事实上, an 就是收敛到特征 向量的迭代向量的 Rayleigh 商. 这种位移选取方法几乎对所有的矩阵都 有三次渐进收敛速度, 但也存在不收敛的例子, 故我们需要对其做改进. 17/102
18 . [ ] (k) (k) an−1 bn−1 (k) Wilkinson 位移: 取 (k) (k) 的最接近 an 的特征值作为位移. bn−1 an 通过计算可得 Wilkinson 位移为 √ ( )2 (k) 1 (k) n + δ − sign(δ) δ + bn−1 σ = a(k) 其中 − a(k) 2 , δ= (a n ). 2 n−1 出于稳定性方面的考虑, 我们通常用下面的计算公式 ( )2 (k) bn−1 n − σ = a(k) √ ( )2 . (k) δ + sign(δ) δ 2 + bn−1 定理 采用 Wilkinson 位移的 QR 迭代是整体收敛的, 且至少是线性收 敛. 事实上, 几乎对所有的矩阵都是渐进三次收敛的. 18/102
19 .例 带 Wilkinson 位移的隐式 QR 迭代算法收敛性演示. Matlab 代码: Eig_TriQR.m 19/102
20 .4 分而治之法 分而治之法由 Cuppen [16] 于 1981 年首次提出, 但直到 1995 年才出现稳 定的实现方式 [33], 是目前计算 所有特征值和特征向量 的最快算法. 考虑不可约对称三对角矩阵 a1 b1 b ... ... 1 .. . am−1 bm−1 bm−1 am bm T = bm am+1 bm+1 .. .. . . bm+1 .. .. . . bn−1 bn−1 an 20/102
21 . a1 b1 b ... ... 1 .. . am−1 bm−1 bm−1 am − bm bm bm = + am+1 − bm bm+1 bm bm .. .. . . bm+1 .. .. . . bn−1 bn−1 an [ ] T1 0 = + bm vv T , 0 T2 其中 v = [0, . . . , 0, 1, 1, 0, . . . , 0]T . 21/102
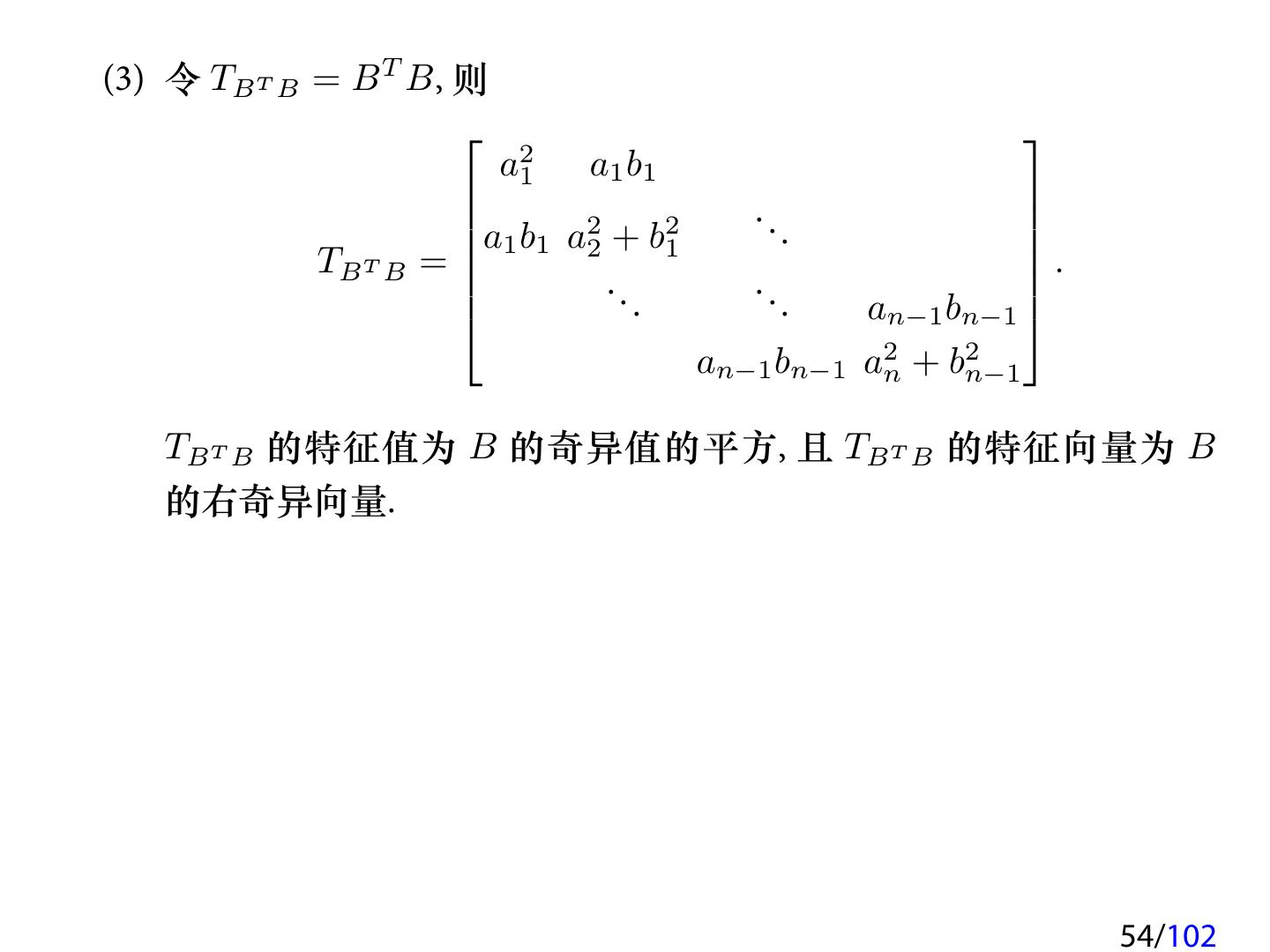
22 .假定 T1 和 T2 的特征值分解已经计算出来了, 即 T1 = Q1 Λ1 QT1 , T2 = Q2 Λ2 QT2 , 下面考虑 T 的特征值分解. [ ] T1 0 T = + bm vv T 0 T2 [ ] Q1 Λ1 QT1 0 = + bm vv T 0 Q2 Λ2 QT2 [ ] ([ ] )[ ]T Q1 0 Λ1 0 T Q1 0 = + bm uu , 0 Q2 0 Λ2 0 Q2 其中 [ ]T [ ] Q1 0 QT1 的最后一列 u= v= . 0 Q2 QT2 的第一列 令 α = bm , D = diag(Λ1 , Λ2 ) = diag(d1 , d2 , . . . , dn ), 并假设 d1 ≥ d2 ≥ · · · ≥ dn . 则 T 的特征值与 D + αuuT 的特征值相同. 22/102
23 .下面考虑 D + αuuT 的特征值. 设 λ 是 D + αuuT 的一个特征值, 若 D − λI 非奇异, 则 det(D + αuuT − λI) = det(D − λI) · det(I + α(D − λI)−1 uuT ). 故 det(I + α(D − λI)−1 uuT ) = 0. 引理 设 x, y ∈ Rn , 则 det(I + xy T ) = 1 + y T x . 于是 ∑ n u2i △ det(I+α(D−λI)−1 uuT ) = 1+αuT (D−λI)−1 u = 1+α = f (λ). i=1 di − λ 故求 A 的特征值等价于求特征方程 f (λ) = 0 的根. 23/102
24 .由于 ∑ n u2i f ′ (λ) = α , i=1 (di − λ)2 当所有的 di 都互不相同, 且所有的 ui 都不为零时, f (λ) 在 λ ̸= di 处都是 严格单调的. 6 4 2 0 −2 −4 −6 −1 0 1 2 3 4 5 6 24/102
25 .所以 f (λ) 在每个区间 (di+1 , di ) 内都有一个根, 共 n − 1 个, 另一个根在 (d1 , ∞) (若 α > 0) 或 (−∞, dn ) (若 α < 0) 中. 由于 f (λ) 在每个区间 (di , di+1 ) 内光滑且严格单调递增 (α > 0) 或递减 (α < 0), 所以在实际计算中, 可以使用对分法, 牛顿法及其变形, 或有理逼 近等算法来求解. 通常都能很快收敛, 一般只需迭代几步即可. 因此, 计算一个特征值的运算量约为 O(n), 计算 D + αuuT 的所有特征值 的运算量约为 O(n2 ). 当所有特征值计算出来后, 我们用下面的引理来计算特征向量. 引理 设 D ∈ Rn×n 为对角矩阵, u ∈ Rn , α ∈ R, 若 λ 是 D + αuuT 的特 征值, 则 (D − λI)−1 u 是其对应的特征向量, 且运算量为 O(n). (板书) 25/102
26 .算法 4.1 计算对称三对角矩阵的特征值和特征向量的分而治之法 1: function [Q, Λ] = dc_eig(T ) % T = QΛQT 2: if T is of 1 × 1 then 3: Q = 1, Λ = T 4: return 5: end if [ ] T1 0 6: form T = + bm vv T 0 T2 7: [Q1 , Λ1 ] = dc_eig(T1 ) 8: [Q2 , Λ2 ] = dc_eig(T2 ) 9: form D + αuuT from Λ1 , Λ2 , Q1 , Q2 compute the eigenvalues Λ and eigenvectors ˆ T 10: [ Q of D] + αuu Q1 0 11: compute the eigenvectors of T with Q = ·Q ˆ 0 Q2 12: end
27 .† 在分而治之法中, 计算特征值和特征值向量是同时进行的. 下面我们详细讨论分而治之算法的几个细节问题: (1) 如何减小运算量; (2) 如何求解特征方程 f (λ) = 0; (3) 如何稳定地计算特征向量. 27/102
28 . (1) 如何减小运算量 — 收缩技巧 (deflation) 分而治之算法的计算复杂性分析如下: 用 t(n) 表示对 n 阶矩阵调用函数 dc_eig 的运算量, 则 t(n) = 2 t(n/2) 递归调用 dc_eig 两次 + O(n2 ) 计算 D + αuuT 的特征值和特征向量 + c · n3 计算 Q. 如果计算 Q 时使用的是稠密矩阵乘法, 则 c = 2; 若不计 O(n2 ) 项, 则由 递归公式 t(n) = 2 t(n/2) + c · n3 可得 t(n) ≈ c · 4n3 /3. 但事实上, 由于收缩 (deflation) 现象的存在, 常数 c 通常比 1 小得多. 28/102
29 .在前面的算法描述过程中, 我们假定 di 互不相等且 ui 不能为零. 事实上, 当 di = di+1 或 ui = 0 时, di 即为 D + αuuT 的特征值, 这种现象 我们称为收缩 (deflation) . 在实际计算时, 当 di − di+1 或 |ui | 小于一个给定的阈值时, 我们就近似认 为 di 为 D + αuuT 的特征值, 即出现收缩现象. 在实际计算中, 收缩现象会经常发生, 而且非常频繁, 所以我们可以而且 应该利用这种优点加快分而治之算法的速度 [16, 53]. 由于主要的计算量集中在计算 Q, 即算法最后一步的矩阵乘积. 如果 ˆ 的第 i 列为 ei , 故计 ui = 0, 则 di 为特征值, 其对应的特征向量为 ei , 即 Q 算 Q 的第 i 列时不需要做任何的计算. 当 di = di+1 时, 也存在一个类似的简化. 29/102