07_子空间迭代

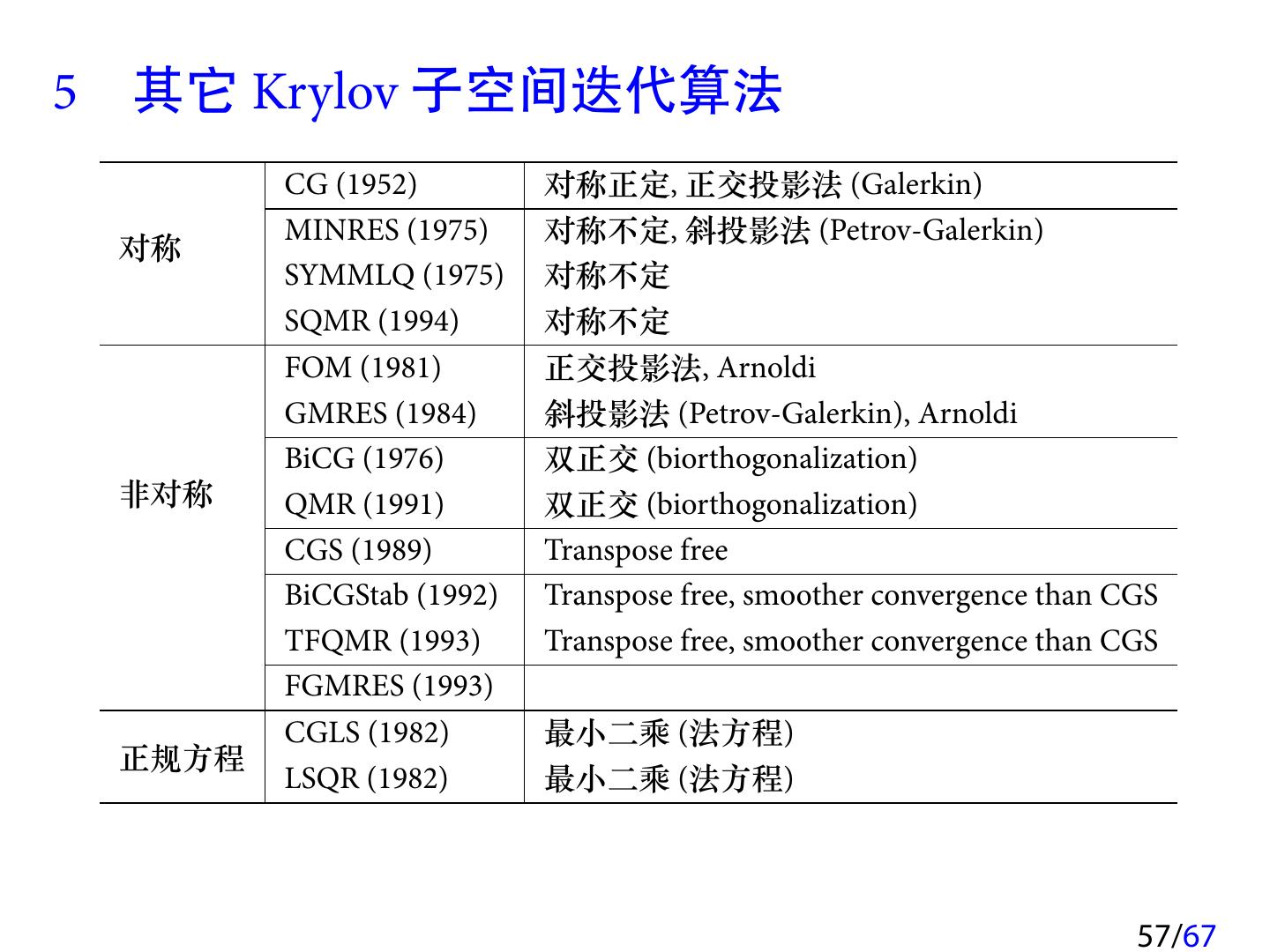
1 .第七讲 子空间迭代方法 1 Krylov 子空间 2 GMRES 算法 3 共轭梯度法 (CG) 4 收敛性分析 5 其它 Krylov 子空间迭代算法 

2 . 基本思想 在一个 维数较低的子空间 中寻找解析解的一个 最佳近似 . 子空间迭代算法的主要过程可以分解为下面三步: (1) 寻找合适的子空间; (2) 在该子空间中求 “最佳近似”; (3) 若这个近似解满足精度要求, 则停止计算; 否则, 重新构造一个新 的子空间, 并返回第 (2) 步. 这里主要涉及到的两个关键问题是: (1) 如果选择和更新子空间; (2) 如何在给定的子空间中寻找 “最佳近似”. 关于第一个问题, 目前较成功的解决方案就是使用 Krylov 子空间 . 2/67 

3 .1 Krylov 子空间 设 A ∈ Rn×n , r ∈ Rn , 则由 A 和 r 生成的 m 维 Krylov 子空间 定义为 Km = Km (A, r) span{r, Ar, A2 r, . . . , Am−1 r}, m ≤ n. 设 dim Km = m, 令 v1 , v2 , . . . , vm 是 Km 的一组基, 则 ∀ x ∈ Km 可表示为 x = y1 v1 + y2 v2 + · · · + ym vm Vm y 寻找 “最佳近似” x(m) 转化为 (1) 寻找一组合适的基 v1 , v2 , . . . , vm ; (2) 求出 x(m) 在这组基下面的表出系数 y (m) . 3/67 

4 . 基的选取: Arnoldi 过程 最简单的基: {r, Ar, A2 r, . . . , Am−1 r} −→ 非正交, 稳定性得不到保证. Arnoldi 过程 : 将 {r, Ar, A2 r, . . . , Am−1 r} 单位正交化 1: v1 = r/∥r∥2 2: for j = 1 to m do 3: z = Avj 4: for i = 1 to j do % MGS 正交化过程 5: hi,j = (vi , z), z = z − hi,j vi 6: end for 7: hj+1,j = ∥z∥2 % if hj+1,j = 0, break, endif 8: vj+1 = z/hj+1,j 9: end for 4/67 

5 . Arnoldi 过程的矩阵表示 记 Vm = [v1 , v2 , . . . , vm ],   h1,1 h1,2 h1,3 ··· h1,m   h2,1 h2,2 h2,3 ··· h2,m     h3,2 h3,3 ··· h3,m    Hm+1,m =  .. .. ..  ∈ R(m+1)×m ,  . . .       hm,m−1 hm,m  hm+1,m 则由 Arnoldi 过程可知 Avj = h1,j v1 + h2,j v2 + · · · + hj,j vj + hj+1,j vj+1 . 所以有 AVm = Vm+1 Hm+1,m = Vm Hm + hm+1,m vm+1 eTm , (7.1) 5/67 

6 .其中 Hm = Hm+1,m (1 : m, 1 : m), em = [0, . . . , 0, 1]T ∈ Rm . 由于 Vm 是列正交矩阵, 上式两边同乘 VmT 可得 VmT AVm = Hm . (7.2) 等式 (7.1) 和 (7.2) 是 Arnoldi 过程的两个重要性质. 6/67 

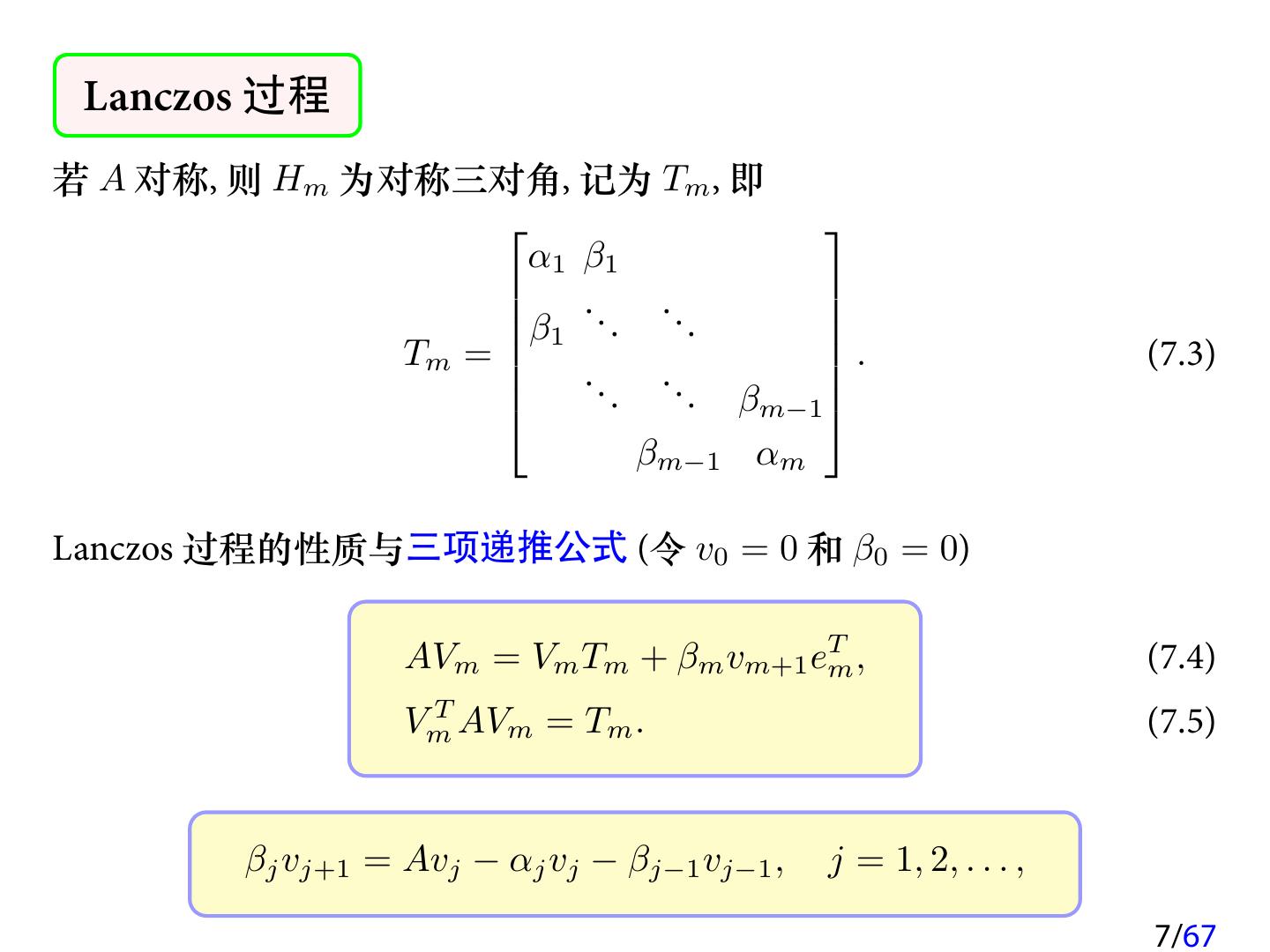
7 . Lanczos 过程 若 A 对称, 则 Hm 为对称三对角, 记为 Tm , 即   α1 β1   β . . . . . .   1  Tm =  . (7.3)  .. ..   . . βm−1  βm−1 αm Lanczos 过程的性质与三项递推公式 (令 v0 = 0 和 β0 = 0) AVm = Vm Tm + βm vm+1 eTm , (7.4) VmT AVm = Tm . (7.5) βj vj+1 = Avj − αj vj − βj−1 vj−1 , j = 1, 2, . . . , 7/67 

8 .Lanczos 过程 1: Set v0 = 0 and β0 = 0 2: v1 = r/∥r∥2 3: for j = 1 to m do 4: z = Avj 5: αj = (vj , z) 6: z = z − αj vj − βj−1 vj−1 7: βj = ∥z∥2 8: if βj = 0 then break, end if 9: vj+1 = z/βj 10: end for 8/67 

9 .Krylov 子空间算法的一般过程 (1) 令 m = 1 (2) 定义 Krylov 子空间 Km (A, r0 ); (3) 找出仿射空间 x(0) + Km 中的 “最佳近似” 解; (4) 如果这个近似解满足精度要求, 则迭代结束; 否则令 m ← m + 1, 返回第 (2) 步. 9/67 

10 .Krylov 子空间迭代算法基本框架 1: Choose an initial guess x(0) 2: computet r0 = b − Ax(0) and v1 = r0 /∥r0 ∥2 3: find the “best” approximate solution x(1) ∈ x(0) +K1 = x(0) +span{v1 } 4: if x(1) is okay then quit end if 5: for m = 2 to n do 6: compute vm with Arnoldi or Lanczos process 7: find the “best” approximate solution 8: x(m) ∈ x(0) + Km = x(0) + span{v1 , . . . , vm } 9: if x(m) is okay then quit end if 10: end for 10/67 

11 . 如何计算 x(0) + Km 中的 “最佳近似” x(m) 首先, 我们必须给出 “最佳” 的定义, 不同的定义会导致不同的算法. 最直接的方式: ∥x(m) − x∗ ∥2 达到最小. 但由于 x∗ 不知道, 因此不实用. 什么是 “最佳” (1) ∥rm ∥2 = ∥b − Ax(m) ∥2 达到最小 A 对称 → MINRES , A 非对称 → GMRES (2) A 对称正定, 极小化 ∥x∗ − x(m) ∥A → CG (共轭梯度法) 本讲主要介绍 GMRES 算法和 CG 算法. 11/67 

12 .2 GMRES 算法 GMRES 算法是目前求解非对称线性方程组的最常用算法之一. “最佳近似” 解的判别方法为 使得 ∥rm ∥2 = ∥b − Ax(m) ∥2 最小 对任意向量 x ∈ x(0) + Km , 可设 x = x(0) + Vm y, 其中 y ∈ Rm . 于是 r = b − Ax = r0 − AVm y = Vm+1 (βe1 − Hm+1,m y) , 这里 β = ∥r0 ∥2 . 由于 Vm+1 列正交, 所以 ∥r∥2 = ∥Vm+1 (βe1 − Hm+1,m y)∥2 = ∥βe1 − Hm+1,m y∥2 . 于是最优性条件就转化为 y (m) = arg minm ∥βe1 − Hm+1,m y∥2 . (7.6) y∈R 用基于 Givens 变换的 QR 分解来求解即可. 12/67 

13 . GMRES 算法的基本框架 算法 2.1 GMRES 迭代算法基本框架 1: 给定初值 x(0) , 停机标准 ε > 0, 以及最大迭代步数 IterMax 2: r0 = b − Ax(0) , β = ∥r0 ∥2 3: v1 = r0 /β 4: for j = 1 to IterMax do 5: w = Avj 6: for i = 1 to j do % Arnoldi 过程 7: hi,j = (vi , w) 8: w = w − hi,j vi 9: end for 10: hj+1,j = ∥w∥2 11: if hj+1,j = 0 then 12: m = j, break 13/67 

14 .13: end if 14: vj+1 = w/hj+1,j 15: relres = ∥rj ∥2 /β % 相对残量 16: if relres< ε then 17: m = j, break 18: end if 19: end for 20: 解最小二乘问题 (7.6), 得到 y (m) 21: x(m) = x(0) + Vm y (m) 14/67 

15 . GMRES 算法的重要性质 定理 设 A ∈ Rn×n , 则 x(m) = arg min ∥b − Ax∥2 (7.7) x∈x(0) +Km 当且仅当 x(m) ∈ x(0) + Km 且 b − Ax(m) ⊥ AKm , (7.8) 其中 AKm = span{Ar, A2 r, . . . , Am r}. 证明: 板书. 15/67 

16 .实施细节 需要解决下面两个问题: (1) 如何计算残量 rm b − Ax(m) 的范数? (2) 如何求解最小二乘问题 (7.6)? 这两个问题可以同时处理. 16/67 

17 . 最小二乘问题的求解 设 Hm+1,m 的 QR 分解为 Hm+1,m = QTm+1 Rm+1,m , 其中 Qm+1 是正交矩阵, Rm+1,m ∈ R(m+1)×m 是上三角矩阵. 则 [ ] Rm ∥βe1 − Hm+1,m y∥2 = ∥βQm+1 e1 − Rm+1,m y∥2 = βq1 − y , 0 2 其中 Rm ∈ R m×m 非奇异 (假定 Hm+1,m 不可约). 所以 −1 y (m) = βRm q1 (1 : m), ∥rm ∥2 = ∥b − Ax(m) ∥2 = ∥βe1 − Hm+1,m y (m) ∥2 = β · |q1 (m + 1)|, 其中 q1 (m + 1) 表示 q1 的第 m + 1 个分量. 17/67 

18 . Hm+1,m 的 QR 分解的递推计算方法 由于 Hm+1,m 是上 Hessenberg 矩阵, 因此我们采用 Givens 变换. [ ] h11 (1) 当 m = 1 时, H21 = , 构造 Givens 变换 G1 使得 h21 [ ] ∗ G1 H21 = = R21 , 即 H21 = GT1 R21 . 0 (2) 假定存在 G1 , G2 , . . . , Gm−1 , 使得 (Gm−1 · · · G2 G1 )Hm,m−1 = Rm,m−1 , 即 Hm,m−1 = (Gm−1 · · · G2 G1 )T Rm,m−1 QTm Rm,m−1 . 18/67 

19 . † 为了书写方便, 这里假定 Gi 的维数自动扩张, 以满足矩阵乘 积的需要. (3) 考虑 Hm+1,m 的 QR 分解. 易知 [ ] Hm,m−1 hm Hm+1,m = , 其中 hm = [h1m , h2m , . . . , hmm ]T . 0 hm+1,m 所以有   [ ] [ ] ˜ m−1 Rm−1 h Qm 0 Rm,m−1 Qm hm  ˆ mm  Hm+1,m = = 0 h , 0 1 0 hm+1,m 0 hm+1,m ˜ m−1 是 Qm hm 的前 m−1 个元素组成的向量, h 其中 h ˆ mm 是 Qm hm 的最后一个元素. 19/67 

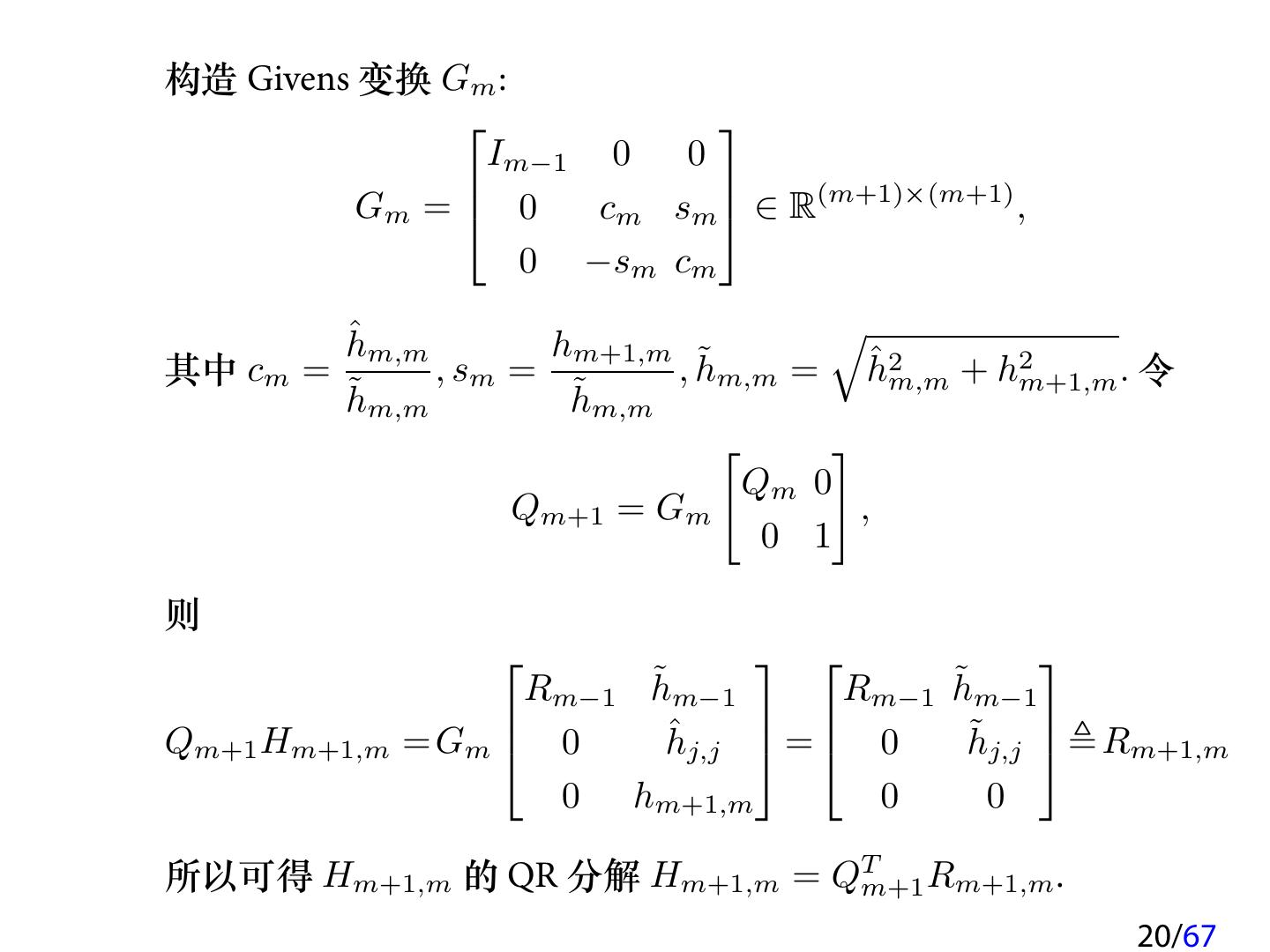
20 .构造 Givens 变换 Gm :   Im−1 0 0   Gm =  0 cm sm  ∈ R(m+1)×(m+1) , 0 −sm cm ˆ m,m √ h hm+1,m ˜ ˆ2 2 其中 cm = , sm = , hm,m = h m,m + hm+1,m . 令 ˜ m,m h ˜ m,m h [ ] Qm 0 Qm+1 = Gm , 0 1 则     ˜ m−1 Rm−1 h ˜ m−1 Rm−1 h  ˆ j,j   ˜ j,j  Qm+1 Hm+1,m = Gm  0 h = 0 h  Rm+1,m 0 hm+1,m 0 0 所以可得 Hm+1,m 的 QR 分解 Hm+1,m = QTm+1 Rm+1,m . 20/67 

21 .† 由 Hm,m−1 的 QR 分解到 Hm+1,m 的 QR 分解, 我们需要 (1) 计算 Qm hm , 即将之前的 m − 1 个 Givens 变换作用到 Hm+1,m 的 最 后 一 列 的 前 m 个 元 素 上, 所 以 我 们 需 要 保 留 所 有 的 Givens 变换; (2) 残量计算: ∥rm ∥2 = |βq1 (m + 1)| = |βQm+1 (m + 1, 1)|, 即 Gm Gm−1 · · · G2 G1 (βe1 ) 的最后一个分量的绝对值. 由于在计算 rm−1 时就已经计算 出 Gm−1 · · · G2 G1 (βe1 ), 因此这里只需做一次 Givens 变换即 可; (3) y (m) 的计算: 当相对残量满足精度要求时, 需要计算 y (m) = −1 Rm q1 (1 : m), 而 q1 即为 Gm Gm−1 · · · G2 G1 (βe1 ). 21/67 

22 . 实用 GMRES 算法 算法 2.2 实用 GMRES 算法 1: 给定初值 x(0) , 停机标准 ε > 0, 最大迭代步数 IterMax 2: r0 = b − Ax(0) , β = ∥r0 ∥2 3: if β < ε then 4: 停止计算, 输出近似解 x(0) 5: end if 6: v1 = r0 /β 7: ξ = βe1 % 记录 q1 8: for j = 1 to IterMax do 9: w = Avj 10: for i = 1 to j do % Arnoldi 过程 11: hi,j = (vi , w) 12: w = w − hi,j vi 22/67 

23 .13: end for 14: hj+1,j = ∥w∥2 15: if hj+1,j = 0 then % 迭代中断 16: m = j, break 17: end if 18: vj+1 = w/hj+1,j 19: for i = 1 to j − 1 do % 计算 Gj−1 · · · G2 G1 Hj+1,j (1 : j, j) [ ] [ ][ ] hij ci si hij 20: = hi+1,j −si ci hi+1,j 21: end for 22: if |hjj | > |hj+1,j | then % 构造 Givens 变换 Gj √ 23: τ = hj+1,j /hjj , cj = 1/ 1 + τ 2 , sj = cj τ 24: else √ 25: τ = hjj /hj+1,j , sj = 1/ 1 + τ 2 , cj = sj τ 26: end if 23/67 

24 .27: hjj = cj hjj + sj hj+1,j % 计算 Gj Hj+1,j (1 : j, j) 28: hj+1,j = 0 [ ] [ ][ ] ξj cj sj ξjj 29: = % 计算 Gj (βGj−1 · · · G2 G1 e1 ) ξj+1 −sj cj ξj+1,j 30: relres = ∥ξj+1 ∥2 /β % 相对残量 31: if relres< ε then 32: m = j, break 33: end if 34: end for 35: m=j 36: y (m) = H(1 : m, 1 : m)\ξ(1 : m) % 最小二乘问题, 回代求解 37: x(m) = x(0) + Vm y (m) 38: if relres< ε then 39: 输出近似解 x 及相关信息 40: else 24/67 

25 .41: 输出算法失败信息 42: end if 25/67 

26 . GMRES 算法的中断 在上面的 GMRES 算法中, 当执行到某一步时有 hj+1,j = 0, 则算法会中断 (breakdown). 如果出现这种中断, 则我们就可以找到精确解. 定理 设 A ∈ Rn×n 非奇异且 r0 ̸= 0. 若 hi+1,i ̸= 0, i = 1, 2, . . . , k − 1, 则 hk+1,k = 0 当且仅当 x(k) 是方程的精确解. (不考虑舍入误差) 证明: 板书. 26/67 

27 . 带重启的 GMRES 算法 由于随着迭代步数的增加, GMRES 算法的每一步所需的运算量和存储量 都会越来越大. 因此当迭代步数很大时, GMRES 算法就不太实用. 重启 : 事先设定一个重启迭代步数 k, 如果 GMRES 达到这个迭代步数时仍不收 敛, 则计算出 x(0) + Kk 中的最佳近似解 x(k) , 然后令 x(0) = x(k) , 重新开 始新的 GMRES 迭代. 27/67 

28 .算法 2.3 带重启的 GMRES 算法 1: 设定重启步数 k (≪ n) 2: 给定初值 x(0) , 停机标准 ε > 0, 最大迭代步数 IterMax 3: r0 = b − Ax(0) , β = ∥r0 ∥2 4: if β < ε then 5: 停止计算, 输出近似解 x = x(0) 6: end if 7: for iter=1 to ceil(IterMax/k) do % 外循环 8: v1 = r0 /β 9: ξ = βe1 10: for j = 1 to k do 11: 调用 GMRES 循环 12: end for 13: m=j 14: y (m) = H(1 : m, 1 : m)\ξ(1 : m) 28/67 

29 .15: x(m) = x(0) + Vm y (m) 16: if relres< ε then % 收敛, 退出循环 17: break 18: end if 19: x(0) = x(m) % 重启 GMRES 20: r0 = b − Ax(0) , β = ∥r0 ∥2 21: end for 22: if relres< ε then 23: 输出近似解 x(m) 及相关信息 24: else 25: 输出算法失败信息 26: end if 29/67