03_线性最小二乘问题

1 .第三讲 线性最小二乘问题 1 引言 2 初等变换矩阵 3 QR 分解 4 奇异值分解 5 线性最小二乘问题的求解方法 6 广义逆与最小二乘 7 最小二乘扰动分析 8 最小二乘问题的推广及其应用 

2 . 最小二乘问题 • 线性最小二乘问题 • 总体最小二乘问题 • 约束最小二乘问题 • ··· ··· 最小二乘问题在统计学, 最优化问题, 材料与结构力学, 信号与图像处理 等方面都有着广泛的应用, 是计算数学的一个重要研究分支, 也是一个活 跃的研究领域. 本讲主要介绍求解线性最小二乘问题的三种直接法. 2/90 

3 .1 引言 考虑线性最小二乘问题 min ∥Ax − b∥22 (3.1) x∈Rn 其中 A ∈ Rm×n , b ∈ Rm . 问题 (3.1) 的解称为最小二乘解. • 当 m = n 且 A 非奇异时, 这就是一个线性方程组, 解为 x = A−1 b; • 当 m < n 时, 未知量个数大于约束个数, 此时我们称问题 (3.1) 为欠 定 (或亚定) 的 (underdetermined). • 当 m > n 时, 约束个数大于未知量个数, 此时我们称问题 (3.1) 为超 定的 (overdetermined); † 为了讨论方便, 本讲总是假定 A 是满秩的. 3/90 

4 .1.1 欠定方程组 若 m < n, 则 Ax = b 存在无穷多个解. 这时我们通常寻求最小范数解, 于 是问题就转化为下面的约束优化问题 1 min ∥x∥22 (3.2) Ax=b 2 对应的 Lagrange 函数为 1 L(x, λ) = ∥x∥22 + λ (Ax − b), 2 其中 λ = [λ1 , λ2 , . . . , λm ] 是 Lagrange 乘子. 此时优化问题 (3.2) 的解就是 L(x, λ) 的鞍点, 即下面方程组的解: ∂L ∂L = x + A λ = 0, = Ax − b = 0. ∂x ∂λ 4/90 

5 .写成矩阵形式为 [ ][ ] [ ] I A x 0 = . A 0 λ b 如果 A (行) 满秩, 即 rank(A) = m, 则系数矩阵非奇异, 上述方程组存在唯 一解. 5/90 

6 .1.2 超定方程组 当 m > n 时, 线性方程组 Ax = b 的解可能不存在. 记 J(x) = ∥Ax − b∥22 . 易知 J(x) 是关于 x 的二次凸函数. 因此, x∗ 是问题 (3.1) 的解当且仅当 x∗ 是 J(x) 的稳定点. 令其一阶导数为零, 可得 A Ax − A b = 0. 于是 (3.1) 就转化为一个 (半正定) 线性方程组. 本讲我们主要讨论超定线性最小二乘问题的求解. 6/90 

7 .2 初等变换矩阵 2.1 初等矩阵 2.2 Gauss 变换 2.3 Householder 变换 2.4 Givens 变换 2.5 正交变换的舍入误差分析 矩阵计算的一个基本思想就是把较复杂的问题转化为等价的较简单的, 易于求解问题. 而完成这个转化的基本工具就是初等变换矩阵, 其中常用 的有三个: Gauss 变换, Householder 变换和 Givens 变换. 7/90 

8 .2.1 初等矩阵 我们考虑初等矩阵 E(u, v, τ ) = I − τ uv ∗ , 其中 u, v ∈ Cn 是非零向量, τ 是一个非零复数. 事实上, E(u, v, τ ) 是单位 矩阵的一个秩 1 扰动. 定理 设 E(u, v, τ ) 是一个初等矩阵, 我们有 (1) det(E(u, v, τ )) = 1 − τ v ∗ u; (2) 若 1 − τ v ∗ u ̸= 0, 则 E(u, v, τ ) 非奇异, 且 τ (E(u, v, τ ))−1 = E(u, v, γ), 其中 γ = . τ v∗ u − 1 (板书) 8/90 

9 .2.2 Gauss 变换 设 lj = [0, . . . , 0, lj+1,j , . . . , ln,j ] , j = 1, 2, . . . , n, 则 Gauss 变换 定义为   1  .   ..       1  △ L(lj ) = E(lj , ej , −1) = I + lj ej =   ,   lj+1,j 1   ..   .. .   .  ln,j 1 向量 lj 称为 Gauss 向量 [Golub-Van Loan 2013]. 由定理 2.1 可知 det(L(lj )) = 1, (L(lj ))−1 = E(lj , ej , 1) = E(−lj , ej , −1) = L(−lj ). Gauss 变换主要用于矩阵的 LU 分解. 9/90 

10 .2.3 Householder 变换 定义 我们称矩阵 2 2 H=I− ∗ vv ∗ = I − vv ∗ , 0 ̸= v ∈ Cn , (3.3) v v ∥v∥22 为 Householder 矩阵 (或 Householder 变换, 或 Householder 反射), 向量 v 称为 Householder 向量. 我们通常将矩阵 (3.3) 记为 H(v). 从几何上看, Householder 变换就是一个关于超平面 span{v}⊥ 的反射. 对任意一个向量 x ∈ Cn , 可将其写为 v∗ x △ x= v + y = αv + y, v∗ v 其中 αv ∈ span{v}, y ∈ span{v}⊥ . 则 2 Hx = x − vv ∗ x = x − 2αv = −αv + y, v∗ v 10/90 

11 .即 Hx 与 x 在 span{v}⊥ 方向有着相同的分量, 而在 v 方向的分量正好相 差一个符号. 也就是说, Hx 是 x 关于超平面 span{v}⊥ 的镜面反射, 见图 2.1. 因此, Householder 矩阵也称为反射矩阵. 图 2.1 Householder 变换的几何意义 11/90 

12 .Householder 矩阵的几个基本性质 定理 设 H ∈ Cn×n 是一个 Householder 矩阵, 则 (1) H ∗ = H, 即 H Hermite 的; (2) H ∗ H = I, 即 H 是酉矩阵; (3) H 2 = I, 所以 H −1 = H ; (4) det(H) = −1; (5) H 有两个互异的特征值: λ = 1 和 λ = −1, 其中 λ = 1 的代数重 数为 n − 1. 12/90 

13 .Householder 矩阵的重要应用: 将一个向量除第一个元素以外的所有元素都化为零 引理 设 x, y ∈ Cn 为任意两个互异的向量, 则存在一个 Householder 矩 阵 H(v) 使得 y = H(v)x 的充要条件是 ∥x∥2 = ∥y∥2 且 x∗ y ∈ R. (取 v = x − y 即可) (板书) 定理 设 x = [x1 , x2 , . . . , xn ] ∈ Rn 是一个非零向量, 则存在 House- holder 矩阵 H 使得 Hx = αe1 , 其中 α = ∥x∥2 (或 α = −∥x∥2 ), e1 = [1, 0, . . . , 0] ∈ Rn . 13/90 

14 .设 x = [x1 , x2 , . . . , xn ] ∈ Rn 是一个实的非零向量, 下面讨论如何计算定 理中的 Householder 矩阵 H(v). 由引理的证明过程可知 v = x − αe1 = [x1 − α, x2 , . . . , xn ] . 在实际计算中, 为了尽可能地减少舍入误差, 我们通常避免两个相近的数 做减法运算, 否则就会损失有效数字. 因此, 我通常取 α = − sign(x1 ) · ∥x∥2 . † 事实上, 我们也可以取 α = sign(x1 )∥x∥2 , 但此时为了减少舍入误差, 我们需要通过下面的公式来计算 v 的第一个分量 v1 α = sign(x1 )∥x∥2 , x21 − ∥x∥22 −(x22 + x23 + · · · + x2n ) v1 = x 1 − α = = . x1 + α x1 + α 14/90 

15 .   x1 − α, if sign(x1 ) < 0 v1 = −(x2 + x2 + · · · + x2 )   2 3 n , otherwise x1 + α 无论怎样选取 α, 我们都有 H = I − βvv ∗ 其中 2 2 2 1 β= ∗ = = =− . v v (x1 − α) + x2 + · · · + xn 2 2 2 2α − 2αx1 2 αv1 15/90 

16 .算法 2.1 计算 Householder 向量 % Given x ∈ Rn , compute β, v such that Hx = ∥x∥2 e1 with H = I − βvv ∗ 1: function [β, v] = house(x) 2: n = length(x) (here length(x) denotes the dimension of x) 3: σ = x22 + x23 + · · · + x2n 4: v = x 5: if σ = 0 then 6: if x1 < 0 then 7: v1 = 2x1 , β = 2/v12 8: else 9: v1 = 0, β = 0 10: end if 11: else √ 12: α = x21 + σ % α = ∥x∥2 13: if x1 < 0 then 16/90 

17 .14: v1 = x1 − α 15: else 16: v1 = −σ/(x1 + α) 17: end if 18: β = 2/(v12 + σ) 19: end if 上 述 算 法 总 运 算 量 大 约 为 3n, 且 具 有 很 好 的 数 值 稳 定 性 ([Wilkinson 1965]). † 在实际计算时, 我们可以将向量 v 单位化, 使得 v1 = 1. 这样, 我们就 无需为 v 另外分配空间, 而是将 v(2 : n) 存放在 x(2 : n) 中, 因为变换 后的向量 x 除第一个分量外, 其它都为零. 17/90 

18 .† 为了避免可能产生的溢出, 可事先将 x 单位化, 即令 x = x/∥x∥2 . 18/90 

19 . Householder 变换的运算量 设 A ∈ Rm×n , H = I − βvv ∗ ∈ Rm , 则 HA = (I − βvv ∗ )A = A − βvv ∗ A = A − βv(A∗ v)∗ . 因此, 在做 Householder 变换时, 并不需要生成 Householder 矩阵, 只需要 Householder 向量即可. 上面矩阵相乘的总运算量大约为 4mn. 19/90 

20 .2.4 Givens 变换   1  ..   .     c s    G(i, j, θ) =   .. .  ∈ Rn×n  (θ ∈ [0, 2π], i ≤ j)    −s c   ..   .  1 Givens 变换 (或 Givens 旋转, 或 Givens 矩阵), 其中 c = cos(θ), s = sin(θ). 定理 G(i, j, θ) 是正交矩阵, 且 det(G(i, j, θ)) = 1. 左乘 Givens 矩阵: 只会影响第 i 行和第 j 行的元素. 右乘 Givens 矩阵: 只会影响第 i 和第 j 列的元素. 20/90 

21 . ] [ c s 例 设 x = [x1 , x2 ] ∈ R , 则存在一个 Givens 变换 G = 2 ∈ R2×2 −s c 使得 Gx = [r, 0] , 其中 c, s 和 r 的值如下: • 若 x1 = x2 = 0, 则 c = 1, s = 0, r = 0 ; • 若 x1 = 0 但 x2 ̸= 0, 则 c = 0, s = x2 /|x2 |, r = |x2 | ; • 若 x1 ̸= 0 但 x2 = 0, 则 c = sign(x1 ), s = 0, r = |x1 | ; √ • 若 x1 ̸= 0 且 x2 ̸= 0, 则 c = x1 /r, s = x2 /r, r = x21 + x22 . 通过 Givens 变换, 我们可以将向量 x ∈ R2 的第二个分量化为 0. 事实上, 对于任意一个向量 x ∈ Rn , 我们都可以通过 Givens 变换将其任 意一个位置上的分量化为 0. 更进一步, 我们也可以通过若干个 Givens 变 换, 将 x 中除第一个分量外的所有元素都化为 0. 21/90 

22 .算法 2.2 Givens 变换 % Given x = [a, b] , compute c, s such that Gx = [r, 0] where r = ∥x∥2 1: function [c, s] = givens(a, b) 2: if b = 0 then 3: if a ≥ 0 then 4: c = 1, s = 0 5: else 6: c = −1, s = 0 7: end if 8: else 9: if |b| > |a| then √ 10: τ = a/b, s = sign(b)/ 1 + τ 2 , c = sτ 11: else √ 12: τ = b/a, c = sign(a)/ 1 + τ 2 , s = cτ 13: end if 14: end if 22/90 

23 .2.5 正交变换的舍入误差分析 引理 设 P ∈ Rn×n 是一个精确的 Householder 或 Givens 变换, P˜ 是其 浮点运算近似, 则 fl(P˜ A) = P (A + E), fl(AP˜ ) = (A + F )P, 其中 ∥E∥2 = O(εu ) · ∥A∥2 , ∥F ∥2 = O(εu ) · ∥A∥2 . 这说明对一个矩阵做 Householder 变换或 Givens 变换是向后稳定的. 考虑对矩阵 A 做一系列的正交变换, 则有 fl(P˜k · · · P˜1 AQ ˜1 · · · Q ˜ k ) = Pk · · · P1 (A + E)Q1 · · · Qk , 其中 ∥E∥2 = O(εu ) · (k∥A∥2 ). 这说明整个计算过程是向后稳定的. 23/90 

24 . ˜ 是其浮点运算近似. 当 X 作 一般地, 假设 X 是一个非奇异的线性变换, X 用到 A 上时, 我们有 = XA + E = X(A + X −1 E) = X(A + F ), △ ˜ fl(XA) 其中 ∥E∥2 = O(εu ) · ∥XA∥2 ≤ O(εu ) · ∥X∥2 · ∥A∥2 , 故 ∥F ∥2 = ∥X −1 E∥2 ≤ O(εu ) · ∥X −1 ∥2 · ∥X∥2 · ∥A∥2 = O(εu ) · κ2 (X) · ∥A∥2 , 因此, 舍入误差将被放大 κ2 (X) 倍. 当 X 是正交变换时, κ2 (X) 达到最小 值 1, 这就是为什么在浮点运算中尽量使用正交变换的原因. 24/90 

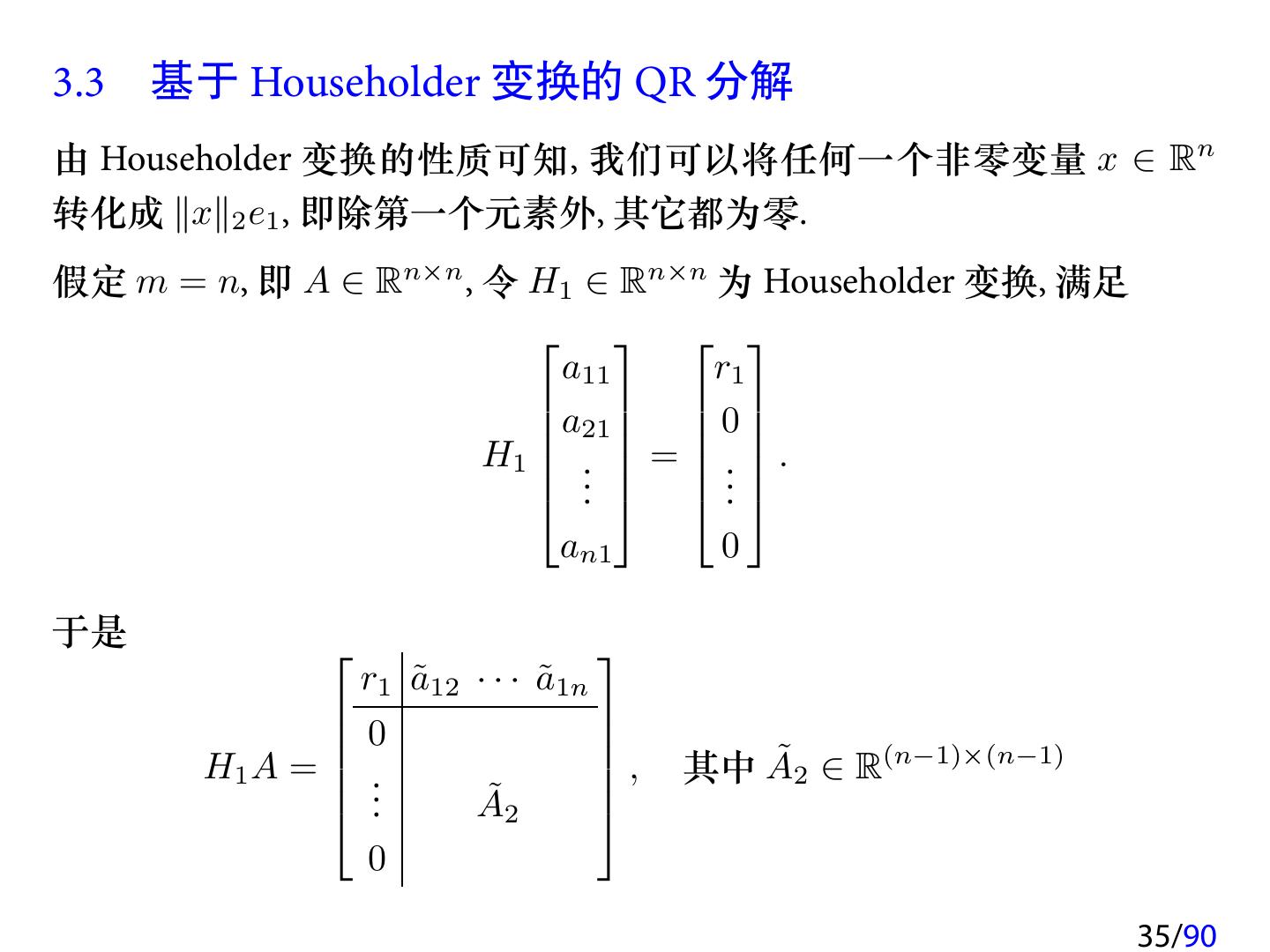
25 .3 QR 分解 3.1 QR 分解的存在唯一性 3.2 基于 MGS 的 QR 分解 3.3 基于 Householder 变换的 QR 分解 3.4 列主元 QR 分解 3.5 基于 Givens 变换的 QR 分解 3.6 QR 分解的稳定性 25/90 

26 .3.1 QR 分解的存在唯一性 定理 (QR 分解) 设 A ∈ Cm×n (m ≥ n). 则存在一个单位列正交矩阵 Q ∈ Cm×n 和一个上三角矩阵 R ∈ Cn×n , 使得 A = QR. (3.4) 证明. 设 A = [a1 , a2 , . . . , an ] ∈ Cm×n . 若 A 列满秩, 即 rank(A) = n. 则 QR 分解 (3.4) 就是对 A 的列向量组进行 Gram-Schmidt 正交化过程的矩阵描述. 具体过程见下面的算法. 26/90 

27 .算法 3.1 Gram-Schmidt Process 1: r11 = ∥a1 ∥2 2: q1 = a1 /r11 3: for j = 2 to n do 4: qj = aj 5: for i = 1 to j − 1 do 6: rij = qi∗ aj % qi∗ 表示共轭转置 7: qj = qj − rij qi 8: end for 9: rjj = ∥qj ∥2 10: qj = qj /rjj 11: end for 27/90 

28 .如果 A 不是列满秩, 我们可以做类似的正交化过程: • 如果 a1 = 0, 则令 q1 = 0; 否则令 q1 = a1 /∥a1 ∥2 ; ∑ • 对于 j = 2, 3, . . . , n, 计算 q˜j = aj − j−1 ∗ i=1 (qi aj )qi . 如果 q˜j = 0, 则令 qj = 0; 否则令 qj = q˜j /∥˜ qj ∥2 . 于是我们有 A = QR, 其中 Q = [q1 , q2 , . . . , qn ] 列正交 (但不是单位列正交, 列向量中可能有零 向量). 这里的 R = [rij ]n×n 是上三角矩阵, 定义如下   q ∗ a , for i ≤ j i j rij =  0, for i > j 易知, 如果 Q 的某一列 qk = 0, 则 R 中对应的第 k 行就全为 0. 28/90 

29 .设 rank(A) = l < n, 则 rank(Q) = l, 即 Q 只有 l 个非零列, 不妨设为 qi1 , qi2 , . . . , qil . 它们构成 Cm 中的一个单位正交向量组. 将其扩展成 Cm 中的一组标准正交基, 即 qi1 , qi2 , . . . , qil , q˜1 , . . . , q˜m−l . 然后我们用 q˜1 替换 Q 中的第一个零列, 用 q˜2 替换 Q 中的第二个零列, 依此类推, 将 Q 中的所有零列都替换掉. 将最后得到的矩阵记为 Q, ˜ 于是 Q∈C ˜ m×n ˜ 单位列正交. 由于 Q 中的新添加的列向量正好与 R 中的零行 相对应, 所以 ˜ = QR = A. QR 这就是 A 的 QR 分解. 29/90