06_线性方程组的迭代解法

1 .第六讲 线性方程组的迭代解法 1 离散 Poisson 方程 2 定常迭代方法 3 收敛性分析 4 加速算法 5 交替方向与 HSS 算法 6 快速 Poisson 算法 

2 .求解线性方程组的常用方法有: • 直接法 : PLU 分解, LDLT 分解, Cholesky 分解等 • 迭代法 : - 经典 (定常, 不动点) 迭代法: Jacobi/Gauss-Seidel, SOR, AOR 等 - Krylov 子空间迭代法: CG, MIRES, GMRES, BiCGStab 等 • 快速算法 : - 基于快速变换, 如 FFT, DCT, DST 等 - 代数多重网格法 (Algebraic multigrid) - 快速多极子算法 (Fast multipole) 有些方法可能只是对某类方程有效, 如快速算法. 在实际应用中, 这些方 法可以结合使用, 如混合 (hybrid) 算法, 预处理算法 (preconditioning) 等. 2/105 

3 .本讲和下一讲将以 Poisson 方程为例, 介绍下面几类算法: • 经典迭代方法: Jacobi, GS, SOR, AOR, SSOR • Krylov 子空间迭代方法: CG, GMRES • 快速 Fourier 变换 (FFT) 和快速 Sine 变换 • 代数多重网格法 更多迭代方法可参见: Templates for the Solution of Linear Systems: Building Blocks for Iterative Methods, SIAM, 1994. 3/105 

4 .1 离散 Poisson 方程 1.1 一维 Poisson 方程 1.2 二维 Poisson 方程 在本讲中, 我们以一个典型的线性方程组为例, 逐个介绍各种迭代方法, 并比较它们之间的性能. 这个方程组就是二维 Poisson 方程经过五点差分 离散后得到的线性方程组. 4/105 

5 .1.1 一维 Poisson 方程 考虑如下带 Dirichlet 边界条件的一维 Poisson 方程  2 − d u(x) = f (x), 0 < x < 1, dx2 (6.1)  u(0) = a, u(1) = b, 其中 f (x) 是给定的函数, u(x) 是需要计算的未知函数. 差分离散 1 取步长 h = n+1 , 节点为 xi = ih, i = 0, 1, 2, . . . , n + 1. 我们采用中心差分离散, 可得 (i = 1, 2, . . . , n) ( ) d2 u(x) 2u(xi ) − u(xi−1 ) − u(xi+1 ) d4 u − = + O h2 · . dx2 xi h2 dx4 ∞ 5/105 

6 .将其代入 (6.1), 舍去高阶项后可得 Poisson 方程在 xi 点的近似离散方程 −ui−1 + 2ui − ui+1 = h2 fi , 其中 fi = f (xi ), ui 为 u(xi ) 的近似. 令 i = 1, 2, . . . , n, 则可得 n 个线性方程, 写成矩阵形式 Tn u = f, (6.2) 其中       2 −1 u1 f1 + u0    u    −1 . . . ..   2   f2   .   .   .  Tn =  ,    u =  ..  , f =  .. . (6.3)  .. ..    . . −1     un−1   fn−1  −1 2 un fn + un+1 6/105 

7 . 系数矩阵 Tn 的性质 引理 Tn 的特征值和对应的特征向量分别为 kπ λk = 2 − 2 cos , n+1 √ [ ]T 2 kπ 2kπ nkπ zk = · sin , sin , . . . , sin , k = 1, 2, . . . , n, n+1 n+1 n+1 n+1 即 Tn = ZΛZ T , 其中 Λ = diag(λ1 , λ2 , . . . , λn ), Z = [z1 , z2 , . . . , zn ]. 证明. 直接代入验证即可. □ 7/105 

8 .引理 更一般地, 设 T = tridiag(a, b, c) ∈ Rn×n , 则 T 的特征值为 √ kπ λk = b − 2 ac cos , k = 1, 2, . . . , n, n+1 对应的特征向量为 zk , 其第 j 个分量为 ( a ) 2j jkπ zk (j) = sin . c n+1 特别地, 若 a = c = 1, 则对应的单位特征向量为 √ [ ]T 2 kπ 2kπ nkπ zk = · sin , sin , . . . , sin . n+1 n+1 n+1 n+1 (证明留作练习) 8/105 

9 .由前面的结论可知, Tn 是对称正定的, 其最大特征值为 ( ) nπ nπ 2 1 − cos = 4 sin2 ≈ 4, n+1 2(n + 1) 最小特征值为 ( ) ( )2 π π π 2 1 − cos 2 = 4 sin ≈ . n+1 2(n + 1) n+1 因此, 当 n 很大时, Tn 的谱条件数约为 4(n + 1)2 κ2 (Tn ) ≈ . π2 9/105 

10 .† 矩阵 Tn 可以分解为 Tn = DDT , 其中   −1 1    −1 1  D=  .. ..  ∈ R n×(n+1) .  . .  −1 1 矩阵 D 也通常称为 差分矩阵. 需要注意的是, D 不是方阵, 因此不能 用这个分解来求解线性方程组 Tn x = b. 10/105 

11 .1.2 二维 Poisson 方程 现在考虑二维 Poisson 方程   2 2 −∆u(x, y) = − ∂ u(x, y) − ∂ u(x, y) = f (x, y), (x, y) ∈ Ω, ∂x2 ∂y 2 (6.4)  u(x, y) = u0 (x, y), (x, y) ∈ ∂Ω 其中 Ω = [0, 1] × [0, 1] 为求解区域, ∂Ω 表示 Ω 的边界. 11/105 

12 . 五点差分离散 1 为了简单起见, 我们在 x-方向和 y-方向取相同的步长 h = n+1 , 节点设为 xi = ih, yj = jh, i, j = 0, 1, 2, . . . , n. 在 x-方向和 y-方向同时采用中心差 分离散可得 ∂ 2 u(x, y) 2u(xi , yj ) − u(xi−1 , yj ) − u(xi+1 , yj ) ≈ ∂x2 (xi ,yj ) h2 2 ∂ u(x, y) 2u(xi , yj ) − u(xi , yj−1 ) − u(xi , yj+1 ) ≈ . ∂y 2 (xi ,yj ) h2 代入 (6.4), 即得二维 Poisson 方程在 (xi , yj ) 点的近似离散方程 4ui,j − ui−1,j − ui+1,j − ui,j−1 − ui,j+1 = h2 fi,j , 其中 fij = f (xi , yj ), ui,j 为 u(xi , yj ) 的近似. 12/105 

13 .写成矩阵形式即为 T u = h2 f, (6.5) 其中 △ T = I ⊗ Tn + Tn ⊗ I, u = [u1,1 , . . . , un,1 , u1,2 , . . . , un,2 , . . . , u1,n , . . . , un,n ]. † 在后面介绍的算法时, 我们都以二维离散 Poisson 方程 (6.5) 为例. 13/105 

14 . 系数矩阵 T 的性质 因为 T = I ⊗ Tn + Tn ⊗ I, 由 Kronecker 乘积的性质即得 定理 设 Tn = ZΛZ T , 其中 Z = [z1 , z2 , . . . , zn ] 为正交阵, Λ = diag(λ1 , λ2 , . . . , λn ) 为对角阵, 则 T 的特征值分解为 T = (Z ⊗ Z)(I ⊗ Λ + Λ ⊗ I)(Z ⊗ Z)T , 即 T 的特征值为 λi + λj , 对应的特征向量为 zi ⊗ zj , i, j = 1, 2, . . . , n. 条件数 nπ nπ 1 − cos sin2 λmax (T ) n+1 = 2(n + 1) 4(n + 1)2 κ(T ) = = π π ≈ . λmin (T ) 1 − cos sin2 π2 n+1 2(n + 1) 故当 n 越来越大时, κ(T ) → ∞, 即 T 越来越病态. 14/105 

15 . 二维离散 Poisson 方程的常用算法 假定网格剖分为 n × n, 并记 ns = n2 . 方法 串行时间 存储空间 直接法 稠密 Cholesky 分解 O(n3s ) O(n2s ) 显式求逆 O(n2s ) O(n2s ) 3/2 带状 Cholesky 分解 O(n2s ) O(ns ) 3/2 稀疏 Cholesky 分解 O(ns ) O(ns log ns ) 经典迭代 Jacobi O(n2s ) O(ns ) Gauss-Seidel O(n2s ) O(ns ) 3/2) SOR O(ns O(ns ) 5/4 带 Chebyshev 加速的 SSOR O(ns ) O(ns ) 3/2 Krylov 子空间迭代 CG (共轭梯度法) O(ns ) O(ns ) 5/4 CG (带修正 IC 预处理) O(ns ) O(ns ) 快速算法 FFT (快速 Fourier 变换) O(ns log ns ) O(ns ) 块循环约化 O(ns log ns ) O(ns ) Multigrid O(ns ) O(ns ) 

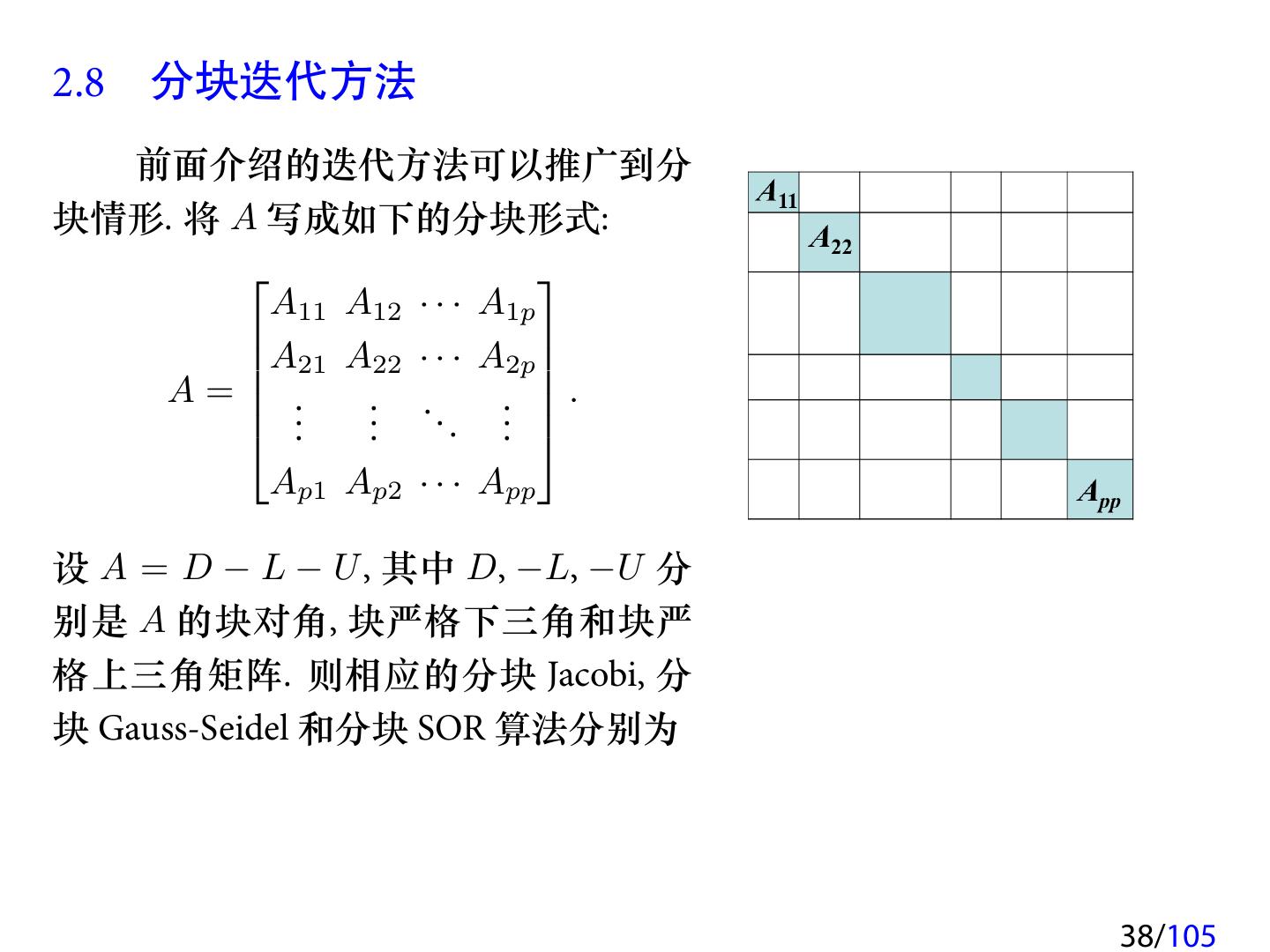
16 .2 定常迭代方法 2.1 矩阵分裂迭代方法 2.2 Jacobi 迭代 2.3 Gauss-Seidel 迭代 2.4 SOR 迭代 2.5 SSOR 迭代方法 2.6 AOR 迭代 2.7 Richardson 算法 2.8 分块迭代方法 16/105 

17 .当直接求解方程组 Ax = b 较困难时, 我们可以求解一个近似方程组 M x = b. 设其解为 x(1) . 易知它与真解之间的误差满足 A(x∗ − x(1) ) = b − Ax(1) . 如果 x(1) 已经满足精度要求, 则停止计算, 否则需要修正. 设修正量为 ∆x. 显然 ∆x 满足方程 A∆x = b − Ax(1) . 但由于直接求解该 方程比较困难, 因此我们还是求解近似 M ∆x = b − Ax(1) . 于是得到修正后的近似解 x(2) = x(1) + ∆x = x(1) + M −1 (b − Ax(1) ). 若 x(2) 已经满足精度要求, 则停止计算, 否则继续按以上的方式进行修正. 17/105 

18 .不断重复以上步骤, 于是, 我们就得到一个序列 x(1) , x(2) , . . . , , x(k) , . . . . 满足以下递推关系 x(k+1) = x(k) + M −1 (b − Ax(k) ), k = 1, 2, . . . . 由于每次迭代的格式是一样的, 因此称为 定常迭代 . 通常, 构造一个好的定常迭代, 需要考虑以下两点: (1) 以 M 为系数矩阵的线性方程组必须要比原线性方程组容易求 解; (2) M 应该是 A 的一个很好的近似, 或者迭代序列 {xk } 要收敛. 18/105 

19 .下面我们就介绍几个常见的基于矩阵分裂的定常迭代方法: • Jacobi 算法 • Gauss-Seidel 算法 • SOR (Successive Over-Relaxation) 算法 • SSOR (Symmetric SOR) 算法 • AOR (Accelerated over-relaxation) 算法 19/105 

20 .2.1 矩阵分裂迭代方法 迭代方法的基本思想: 给定一个迭代初始值 x(0) , 通过一定的迭代格式生 成一个迭代序列 {x(k) }∞ k=0 , 使得 lim x(k) = x∗ ≜ A−1 b. k→∞ 定义 (矩阵分裂 Matrix splitting) 设 A ∈ Rn×n 非奇异, 称 A=M −N (6.6) 为 A 的一个矩阵分裂, 其中 M 非奇异. 原方程组等价于 M x = N x + b. 于是我们就可以构造出以下的迭代格式 x(k+1) = M −1 N x(k) + M −1 b = Gx(k) + g △ , k = 0, 1, . . . , (6.7) 其中 G = M −1 N 称为该迭代格式的迭代矩阵. 20/105 

21 .2.2 Jacobi 迭代 将矩阵 A 分裂为 A=D−L−U , 其中 D 为 A 的对角线部分, −L 和 −U 分别为 A 的严格下三角和严格上 三角部分. 在矩阵分裂 A = M − N 中取 M = D, N = L + U , 则可得 Jacobi 迭代算 法: x(k+1) = D−1 (L + U )x(k) + D−1 b , k = 0, 1, 2, . . . . (6.8) 迭代矩阵为 GJ = D−1 (L + U ) . 21/105 

22 .写成分量形式即为   1  ∑ n aij xj  (k+1) (k) xi = bi − , i = 1, 2, . . . , n. aii j=1,j̸=i (k+1) † 由于 Jacobi 迭代中 xi 的更新顺序与 i 无关, 即可以按顺序 i = 1, 2, . . . , n 计算, 也可以按顺序 i = n, n − 1, . . . , 2, 1 计算, 或者乱序 计算. 因此 Jacobi 迭代非常适合并行计算. 22/105 

23 .算法 2.1 求解线性方程组的 Jacobi 迭代方法 1: Choose an initial guess x(0) 2: while not converge do 3: for i = 1 to n ( do ) ∑ n / (k+1) (k) 4: xi = bi − aij xj aii j=1,j̸=i 5: end for 6: end while 我们也可以将 Jacobi 迭代格式写为 x(k+1) = x(k) + D−1 (b − Ax(k) ) = x(k) + D−1 rk , k = 0, 1, 2, . . . , △ 其中 rk = b − Ax(k) 是 k 次迭代后的残量. 23/105 

24 . 二维离散 Poisson 方程的 Jacobi 迭代方法 算法 2.2 求解二维离散 Poisson 方程的 Jacobi 迭代方法 1: Choose an initial guess v (0) 2: while not converge do 3: for i = 1 to N do 4: for j = 1 to N(do ) (k+1) (k) (k) (k) (k) 5: ui,j = h2 fi,j + ui+1,j + ui−1,j + ui,j+1 + ui,j−1 /4 6: end for 7: end for 8: end while 24/105 

25 .2.3 Gauss-Seidel 迭代 取 M = D − L, N = U , 即可得 Gauss-Seidel (G-S) 迭代算法: x(k+1) = (D − L)−1 U x(k) + (D − L)−1 b . (6.9) 迭代矩阵为 GGS = (D − L)−1 U . 将 G-S 迭代改写为 Dx(k+1) = Lx(k+1) + U x(k) + b, 即可得分量形式   (k+1) 1  ∑ i−1 (k+1) ∑n (k)  xi = bi − aij xj − aij xj , i = 1, 2, . . . , n. aii j=1 j=i+1 25/105 

26 .算法 2.3 求解线性方程组的 G-S 迭代方法 1: Choose an initial guess x(0) 2: while not converge do 3: for i = 1 to n do ( ) (k+1) 1 ∑ i−1 (k+1) ∑n (k) 4: xi = bi − aij xj − aij xj aii j=1 j=i+1 5: end for 6: end while G-S 算法的主要优点是充分利用了已经获得的最新数据. 但由于 G-S 算法中未知量的更新是按自然顺序进行的. 因此不适合并行 计算. 26/105 

27 .G-S 算法的并行计算: 红黑排序 下面我们介绍一种适合并行计算的更 新顺序: 红黑排序, 即将二维网格点依 次做红黑记号, 如右图所示. 在计算过程中, 对未知量的值进行更 新时, 我们可以先更新红色节点, 此时 所使用的只是黑色节点的数据, 然后 再更新黑色节点, 这时使用的是红色 节点的数据. 于是我们得到红黑排序 G-S 迭代方法. 由于在更新红点时, 各个点之间是相 互独立的, 因此可以并行计算. 同样, 在更新黑点时, 各个点之间也是相互 独立的, 因此也可以并行计算. 27/105 

28 .算法 2.4 求解二维离散 Poisson 方程的红黑排序 G-S 迭代方法 1: Choose an initial guess v (0) 2: while not converge do 3: for (i, j) 为红色节点 do (k+1) 1( 2 (k) (k) (k) (k) ) 4: ui,j = h fi,j + ui+1,j + ui−1,j + ui,j+1 + ui,j−1 4 5: end for 6: for (i, j) 为黑色节点 do (k+1) 1( 2 (k+1) (k+1) (k+1) (k+1) ) 7: ui,j = h fi,j + ui+1,j + ui−1,j + ui,j+1 + ui,j−1 4 8: end for 9: end while 28/105 

29 .2.4 SOR 迭代 在 G-S 算法的基础上, 我们可以通过引入一个松弛参数 ω 来加快收敛 速度. 这就是 SOR (Successive Overrelaxation) 算法, 即将 G-S 算法中的第 k + 1 步近似解与第 k 步近似解做一个加权平均: ( ) x(k+1) = (1 − ω)x(k) + ω D−1 (Lx(k+1) + U x(k) ) + D−1 b . (6.10) 整理后即为 ( ) x(k+1) = (D − ωL)−1 (1 − ω)D + ωU x(k) + ω(D − ωL)−1 b, (6.11) 其中 ω 称为松弛参数. 当 ω = 1 时, SOR 即为 G-S 算法, 当 ω < 1 时, 称为低松弛 (under relaxation) 算法, 当 ω > 1 时, 称为超松弛 (over relaxation) 算法. SOR 算法曾经在很长一段时间内是科学计算中求解线性方程组的首选方 法. 在大多数情况下, 当 ω > 1 时会取得比较好的收敛效果. 29/105