04_非对称特征值问题

1 .第四讲 非对称特征值问题 1 幂迭代 2 反迭代 3 正交迭代 4 QR 迭代 5 带位移的隐式 QR 迭代 6 特征向量的计算 7 广义特征值问题 8 应用：多项式求根 

2 . 非对称矩阵特征值/特征向量的计算 基本约定 1： A ∈ Rn×n 、 非对称 、 稠密 基本约定 2： |λ1 | ≥ |λ2 | ≥ · · · ≥ |λn | ≥ 0 本讲主要讨论如何计算 A 的全部特征值和/或特征向量. 主要介绍以下方法: • 幂迭代方法 • 反迭代方法（位移策略，Rayleigh 商迭代） • 正交迭代方法 • QR 方法 2/78 

3 .关于稠密矩阵特征值计算的参考资料有： • J. H. Wilkinson, The Algebraic Eigenvalue Problem, 1965 • B. N. Parlett, The Symmetric Eigenvalue Problem, 2nd Eds., 1998 • G. W. Stewart, Matrix Algorithms, Vol II: Eigensystems, 2001 • G. H. Golub and C. F. Van Loan, Matrix Computations, 2013 • P. Arbenz, The course 252-0504-00 G, Numerical Methods for Solving Large Scale Eigenvalue Problems, 2018. （该课程的主页） 

4 .1 幂迭代 幂迭代 是计算特征值和特征向量的一种简单易用的算法. 虽然简单, 但它却建立了计算特征值和特征向量的算法的一个基本框架. 算法 1.1 幂迭代算法 (Power Iteration) 1: Choose an initial guess x(0) with ∥x(0) ∥2 = 1 2: set k = 0 3: while not convergence do 4: y (k+1) = Ax(k) 5: x(k+1) = y (k+1) /∥y (k+1) ∥2 6: µk+1 = (x(k+1) , Ax(k+1) ) % 内积 7: k =k+1 8: end while 4/78 

5 . 幂迭代的收敛性 假设 1: A ∈ Rn×n 可对角化, 即 A = V ΛV −1 , 其中 Λ = diag(λ1 , . . . , λn ), V = [v1 , . . . , vn ] ∈ Cn×n , ∥vi ∥2 = 1 假设 2: |λ1 | > |λ2 | ≥ |λ3 | ≥ · · · ≥ |λn |. 由于 V 的列向量组构成 Cn 的一组基, 因此 x(0) 可表示为 x(0) = α1 v1 + α2 v2 + · · · + αn vn = V [α1 , α2 , . . . , αn ] . 我们假定 α1 ̸= 0, 即 x(0) 不属于 span{v2 , v3 , . . . , vn } (由于 x(0) 是随机选取的, 从概率意义上讲, 这个假设通常是成立的). 5/78 

6 .于是我们可得       α1 α1 α1 λk1        α2   α2   α2 λk2  Ak x(0) = (V ΛV −1 )k V   k   ..  = V Λ  ..  = V  .   .   .   .   .  αn αn αn λkn   1  ( )k   α2 λ2     k  α1 λ1  = α1 λ1 V  . ..   .     αn ( λn )k  α1 λ1 又 |λi /λ1 | < 1, i = 2, 3, . . . , n, 所以 ( )k λi lim = 0, i = 2, 3, . . . , n. k→∞ λ1 6/78 

7 .故当 k 趋向于无穷大时, 向量 [ ( )k ( )k ] α2 λ2 αn λn 1, , ..., , k = 0, 1, 2, . . . α1 λ1 α1 λ1 收敛到 e1 = [1, 0, . . . , 0] . 所以向量 x(k) = Ak x(0) /∥Ak x(0) ∥2 收敛到 ±v1 , 即 λ1 的特征向量. 而 µk = (x(k) )∗ Ax(k) 则收敛到 v1∗ Av1 = λ1 . † 幂迭代的收敛快慢取决于 |λ2 /λ1 | 的大小, |λ2 /λ1 | 越小, 收敛越快. • 幂迭代只能用于计算 (模) 最大的特征值和其相应的特征向量. • 当 |λ2 /λ1 | 接近于 1 时, 收敛速度会非常慢. • 如果模最大的特征值是一对共轭复数, 则幂迭代可能会失效. 7/78 

8 .1.1 位移策略 出发点: 加快幂迭代算法的收敛速度 ⇐⇒ 尽可能地减小 |λ2 /λ1 | 策略: 位移策略 (shift), 即计算 A − σI 的特征值 我们称 σ 为位移 (shift), 满足 (1) λ1 − σ 是 A − σI 的模最大的特征值; λi − σ (2) max 尽可能地小. 2≤i≤n λ1 − σ 其中第一个条件保证最后所求得的特征值是我们所要的, 第二个条件用 于加快幂迭代的收敛速度. 缺点: (1) σ 很难选取; (2) 加速效果有限 改进方法: 与反迭代相结合, 能起到很好的加速效果 8/78 

9 .2 反迭代 用幂迭代求 A−1 的模最小特征值, 这就是反迭代 算法 2.1 反迭代算法 (Inverse Iteration) 1: Choose a scalar σ and an initial vector x(0) with ∥x(0) ∥2 = 1 2: set k = 0 3: while not convergence do 4: y (k+1) = (A − σI)−1 x(k) 5: x(k+1) = y (k+1) /∥y (k+1) ∥2 6: µk+1 = (x(k+1) , Ax(k+1) ) 7: σ = µk+1 , k = k + 1 8: end while 显然: µk 收敛到距离 σ 最近的特征值, x(k) 收敛到对应的特征向量 9/78 

10 .† 事实上, 反迭代 + 位移策略, 可以计算矩阵的任意一个特征值 优点: • 若 σ 与某个特征值 λk 非常接近, 则反迭代算法的收敛速度非常快. • 只要选取合适的位移 σ, 就可以计算 A 的任意一个特征值. 缺点: • 每步迭代需要解一个线性方程组 (A − σI)y (k+1) = x(k) , 这需要对 A − σI 做 LU 或 PLU 分解. • 与幂迭代一样, 反迭代算法一次只能求一个特征值. • 怎样选取位移 σ? → Rayleigh 商: 动态选取, 自动调整 10/78 

11 .2.1 Rayleigh 商迭代 出发点: 使得 σ 与所求的特征值越靠近越好. 期望能直接给出一个理想位移是不太现实的. 比较现实的方法就是动态 调整, 使得位移逐渐靠近某个特征值. Rayleigh 商迭代: 以 Rayleigh 商 µk 为第 k 步的位移 理由: µk 会逐渐收敛到某个特征值. 11/78 

12 .算法 2.2 Rayleigh 商迭代 (Rayleigh Quotient Iteration, RQI) 1: Choose an initial vector x(0) with ∥x(0) ∥2 = 1 2: set k = 0 3: compute σ = (x(0) )∗ Ax(0) 4: while not converge do 5: y (k+1) = (A − σI)−1 x(k) 6: x(k+1) = y (k+1) /∥y (k+1) ∥2 7: µk+1 = (x(k+1) , Ax(k+1) ) 8: σ = µk+1 9: k =k+1 10: end while 12/78 

13 .RQI 算法的收敛性 一般来说, 如果 Rayleigh 商迭代收敛到 A 的一个单特征值, 则至少是二 次收敛的, 即具有局部二次收敛性. 如果 A 是对称的, 则能达到局部三 次收敛, 详情见后面的对称特征值问题. 缺点: 由于每次迭代的位移是不同的, 因此每次迭代需要求解一个不同的线性 方程组, 这使得运算量大大增加. 因此通常应用于 三对角矩阵 的特征值计算. 13/78 

14 .3 正交迭代 出发点: 同时计算多个特征值/特征向量 策略: 同时采用多个初始向量, 希望收敛到 A 的一个不变子空间 算法 3.1 正交迭代算法 (Orthogonal Iteration) 1: Choose an n × p column orthogonal matrix Z0 2: set k = 0 3: while not convergence do 4: compute Yk+1 = AZk 5: Yk+1 = Zk+1 Rˆ k+1 % QR 分解 6: k =k+1 7: end while 14/78 

15 .说明: 在算法中使用 QR 分解是为了保持 Zk 的列正交性, 使得其列向量组构 成子空间 span{Ak Z0 } 的一组正交基. 一方面提高算法的数值稳定性, 另一方面避免所有列都收敛到最大特征值所对应的特征向量. 15/78 

16 . 收敛性分析 假设 A 是可对角化的, 即 A = V ΛV −1 , 其中 Λ = diag(λ1 , λ2 , . . . , λn ), 且 |λ1 | ≥ · · · ≥ |λp | > |λp+1 | ≥ · · · ≥ |λn |. 则可得 span{Zk } = span{Yk } = span{AZk−1 }, k = 1, 2, . . . , 由此可知 span{Zk } = span{Ak Z0 } = span{V Λk V −1 Z0 }. 我们注意到   (λ1 /λp )k  ..   .  [ ]   (k)   −1 k Wp Λk V −1 Z0 = λkp  △ 1  V Z0 = λ p .   W (k)  ..  n−p  .  (λn /λp )k 16/78 

17 . (k) 由于当 i > p 时有 |λi /λp | < 1, 所以当 k 趋于无穷大时, Wn−p 趋向于 0. 令 V = [Vp , Vn−p ], 则 [ ] Wp (k) ( ) k −1 k k (k) (k) V Λ V Z0 = λp [Vp , Vn−p ] (k) = λ p Vp W p + V n−p W n−p . Wn−p 所以当 k → ∞ 时, 有 span{Zk } = span{V Λk V −1 Z0 } = span{Vp Wp(k) + Vn−p Wn−p } (k) → span{Vp Wp(k) } = span{Vp }, 即 span{Zk } 趋向于 A 的一个 p 维不变子空间 span{Vp }. 定理 给定正整数 p (1 ≤ p ≤ n), 考虑算法 3.1 . 假设 A 是可对角化的, 且 |λ1 | ≥ · · · ≥ |λp | > |λp+1 | ≥ · · · ≥ |λn |. 则 span{Zk } 收敛到 A 的一 个 p 维不变子空间. 17/78 

18 .说明: 如果 A 不可对角化, 利用 Jordan 标准型, 可以到同样的结论, 见 [Watkins 2007, Watkins-Elsner 1991]. † 在正交迭代中, 如果我们取 Z0 = I, 则可得到一类特殊的正交迭代算 法. 此时, 在一定条件下, 正交迭代会收敛到 A 的 Schur 标准型. 18/78 

19 .4 QR 迭代 4.1 算法介绍 4.2 QR 迭代与幂迭代的关系 4.3 QR 迭代与反迭代的关系 4.4 QR 迭代与正交迭代的关系 4.5 QR 迭代的收敛性 4.6 带位移的 QR 迭代 19/78 

20 .4.1 算法介绍 基本思想: 通过不断的正交相似变换, 将 A 转化为 (拟) 上三角形式 算法 4.1 QR 迭代算法 (QR Iteration) 1: Set A1 = A and k = 1 2: while not convergence do 3: Ak = Qk Rk % QR 分解 4: compute Ak+1 = Rk Qk 5: k =k+1 6: end while 20/78 

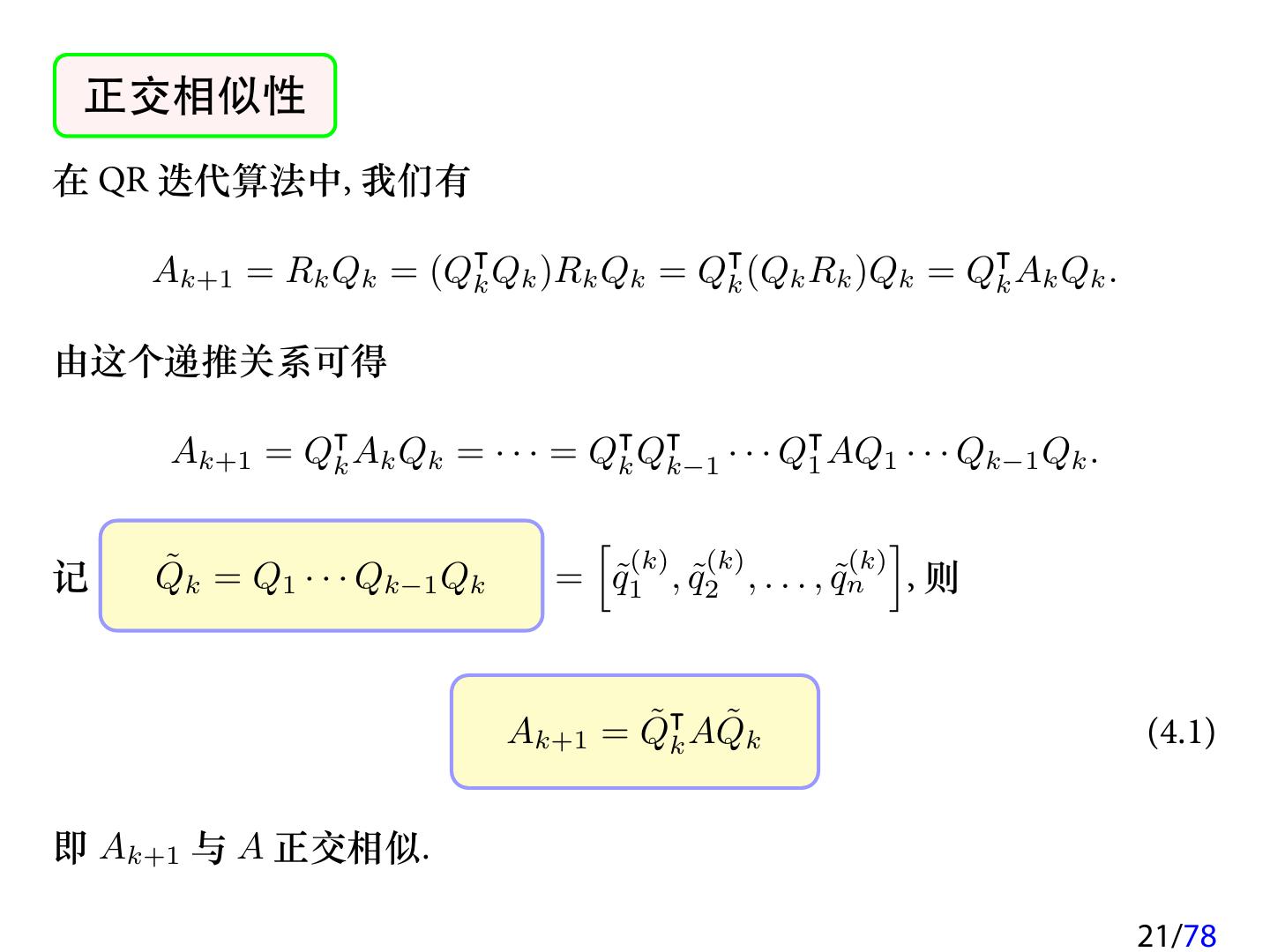
21 . 正交相似性 在 QR 迭代算法中, 我们有 Ak+1 = Rk Qk = (Qk Qk )Rk Qk = Qk (Qk Rk )Qk = Qk Ak Qk . 由这个递推关系可得 Ak+1 = Qk Ak Qk = · · · = Qk Qk−1 · · · Q1 AQ1 · · · Qk−1 Qk . [ ] ˜ k = Q1 · · · Qk−1 Qk (k) (k) (k) 记 Q = q˜1 , q˜2 , . . . , q˜n , 则 ˜ AQ Ak+1 = Q ˜k (4.1) k 即 Ak+1 与 A 正交相似. 21/78 

22 .4.2 QR 迭代与幂迭代的关系 记 ˜ k = Rk Rk−1 · · · R1 R , 则有 ˜kR Q ˜k = Q ˜ k−1 (Qk Rk )R ˜ k−1 = Q ˜ k−1 (Ak )R ˜ k−1 =Q˜ k−1 (Q ˜ AQ˜ k−1 )R ˜ k−1 k−1 ˜ k−1 R = AQ ˜ k−1 , 由此递推下去, 即可得 ˜kR Q ˜ k = Ak−1 Q ˜1R ˜ 1 = Ak−1 Q1 R1 = Ak 故 ˜kR Q ˜ k e 1 = Ak e 1 22/78 

23 .假设 |λ1 | > |λ2 | ≥ · · · ≥ |λn |, 则当 k 充分大时, Ak e1 收敛到 A 的模最大 特征值 λ1 所对应的特征向量. ➩ (k) ˜ k 的第一列 q˜ 也收敛到 λ1 所对应的特征向量 故Q 1 (k) (k) q1 → λ1 q˜1 因此, 当 k 充分大时, A˜ ˜ AQ 由 Ak+1 = Q ˜ k 可知, Ak+1 的第一列 k (k) ˜ ˜(k) = λ1 e1 k q1 → λ1 Qk q ˜ A˜ Ak+1 (:, 1) = Q 1 结论 Ak+1 的第一列的第一个元素收敛到 λ1 , 而其它元素都趋向于 0. 收敛速度取决于 |λ2 /λ1 | 的大小. 23/78 

24 .4.3 QR 迭代与反迭代的关系 ˜ k 的最后一列. 由 Ak+1 = Q 观察 Q ˜ AQ ˜ k 可知 k ˜k = Q AQ ˜ k Ak+1 = Q ˜ k Qk+1 Rk+1 = Q ˜ k+1 Rk+1 , 所以有 ˜ k R−1 . ˜ k+1 = AQ Q k+1 ˜ k+1 和 Q 由于 Q ˜ k 都是正交矩阵, 上式两边转置后求逆, 可得 ( )−1 (( ) )−1 −1 ˜ ˜ k+1 = Q Q ˜ k+1 = R−1 ˜ A Q k+1= (A ) Q kR k k+1 . 观察等式两边矩阵的最后一列, 可得 −1 (k) q˜n(k+1) = c1 (A ) q˜n , (c1 为某个常数) 依此类推, 可知 −k q˜n(k+1) = c (A ) q˜n(1) (c 为某个常数) 24/78 

25 . −1 假定 |λ1 | ≥ · · · ≥ |λn−1 | > |λn | > 0, 则 λ−1 n 是 (A ) 的模最大特征值. 收敛到 λ−1 (k+1) 由幂迭代可知, q˜n n 所对应的特征向量, 即 −1 (k+1) (A ) q˜n → λ−1 n q˜n(k+1) (k → ∞) 所以 A q˜n(k) → λn q˜n(k) (k → ∞) ˜ AQ 由 Ak+1 = Q ˜ k 可知, A k k+1 的最后一列 ˜ A q˜n(k) → λn Q Ak+1 (:, n) = Q ˜ q˜n(k) = λn en . k k 结论 Ak+1 的最后一行的最后一个元素收敛到 λn , 而其它元素都趋向于 0. 收敛速度取决于 |λn /λn−1 | 的大小. 25/78 

26 .4.4 QR 迭代与正交迭代的关系 下面的定理给出了 QR 迭代算法与正交迭代算法 (Z0 = I) 之间的关系. 定理 假定正交迭代算法 3.1 和 QR 算法 4.1 中所涉及的 QR 分解都是唯 一的. Ak 是由 QR 迭代算法 4.1 生成的矩阵, Zk 是由正交迭代算法 3.1 (取 Z0 = I) 生成的矩阵, 则有 Ak+1 = Zk AZk . (板书) 26/78 

27 .4.5 QR 迭代的收敛性 定理 设 A = V ΛV −1 ∈ Rn×n , 其中 Λ = diag(λ1 , λ2 , . . . , λn ), 且 |λ1 | > |λ2 | > · · · > |λn |. 若 V −1 的所有主子矩阵都非奇异（即 V −1 存在 LU 分解）, 则 Ak 的对角线以下的元素均收敛到 0. (板书) 说明: 需要指出的是, 由于 Dk 的元素不一定收敛, 故 Ak+1 对角线以上（不含 对角线）的元素不一定收敛, 但这不妨碍 Ak+1 的对角线元素收敛到 A 的特征值（即 Ak+1 的对角线元素是收敛的）. 27/78 

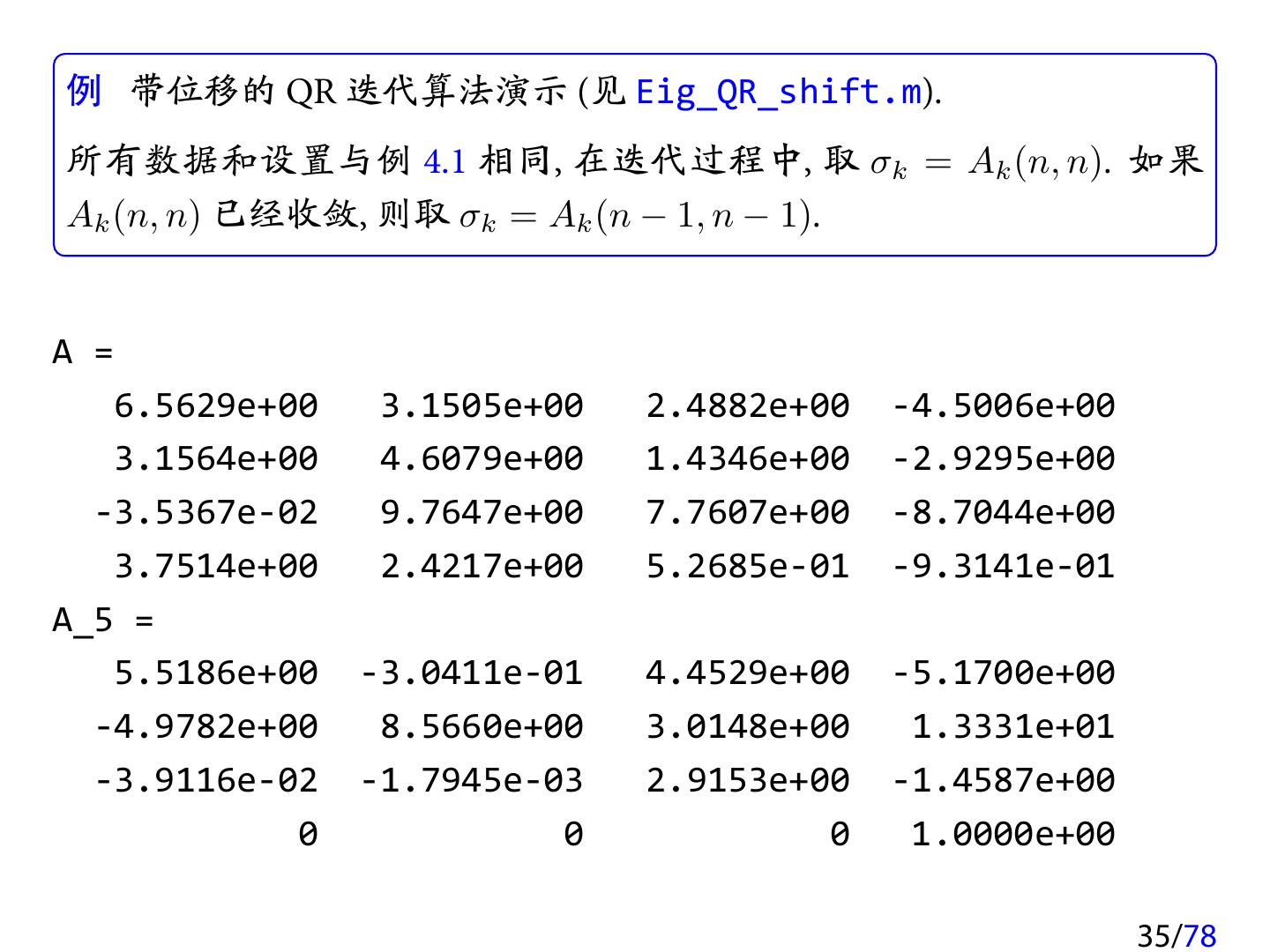
28 .例 QR 迭代算法演示 (见 Eig_QR_demo.m). 设   9  5    −1 A=X X ,  3  1 其中 X 是由 MATLAB 随机生成的非奇异矩阵. 在迭代过程中, 对于 Ak 的下三角部分中元素, 如果其绝对值小于某个阈 值 tol, 则直接将其设为 0, 即 (k) (k) aij = 0 if i > j and |aij | < tol. 这里我们取 tol = 10−6 max {|aij |}, 迭代过程如下: (k) 1≤i,j≤n 28/78 

29 .A = 6.5629e+00 3.1505e+00 2.4882e+00 -4.5006e+00 3.1564e+00 4.6079e+00 1.4346e+00 -2.9295e+00 -3.5367e-02 9.7647e+00 7.7607e+00 -8.7044e+00 3.7514e+00 2.4217e+00 5.2685e-01 -9.3141e-01 A_7 = 1.0079e+01 2.0598e+00 -8.7382e-02 -1.4010e+01 -2.6356e+00 3.9694e+00 5.3709e+00 2.8474e+00 -1.0317e-02 -1.8888e-02 2.9523e+00 -1.4913e+00 0 -1.4296e-05 1.3377e-03 9.9898e-01 A_8 = 9.8306e+00 3.5979e+00 -1.4282e+00 1.4272e+01 -1.1084e+00 4.1983e+00 5.1778e+00 7.8545e-01 -2.9432e-03 -1.2199e-02 2.9714e+00 1.5095e+00 0 0 -4.5563e-04 9.9966e-01 29/78