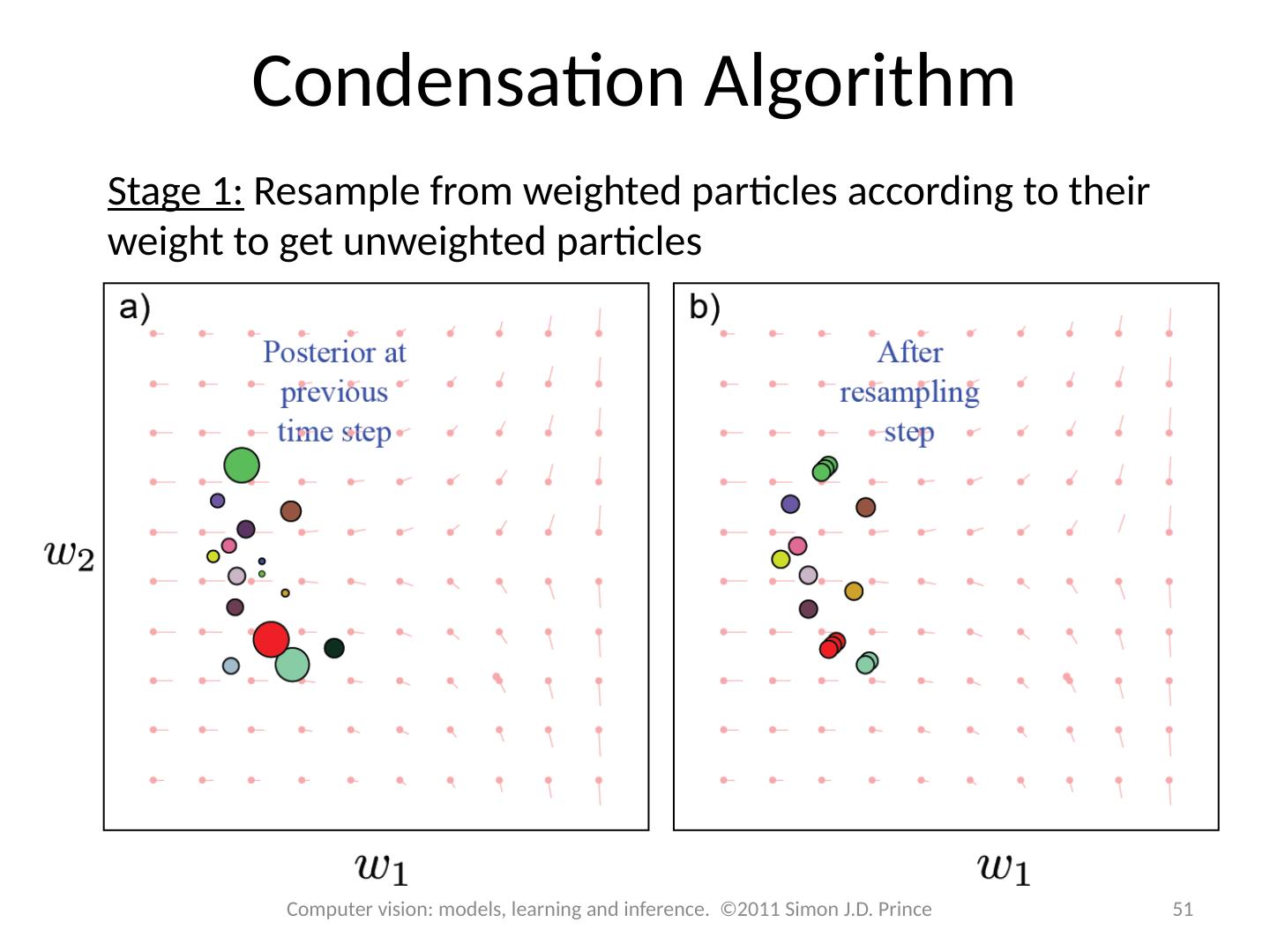
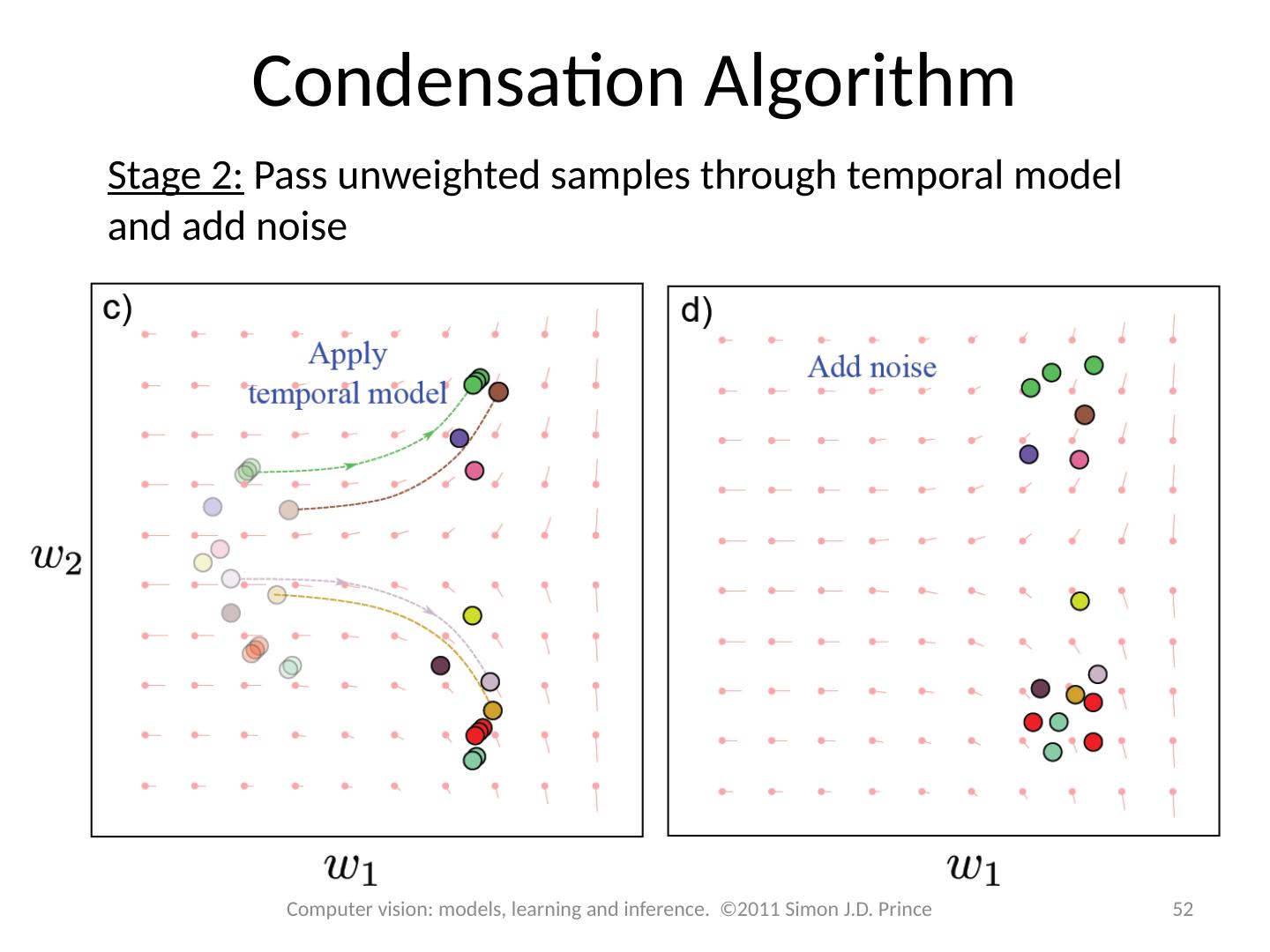
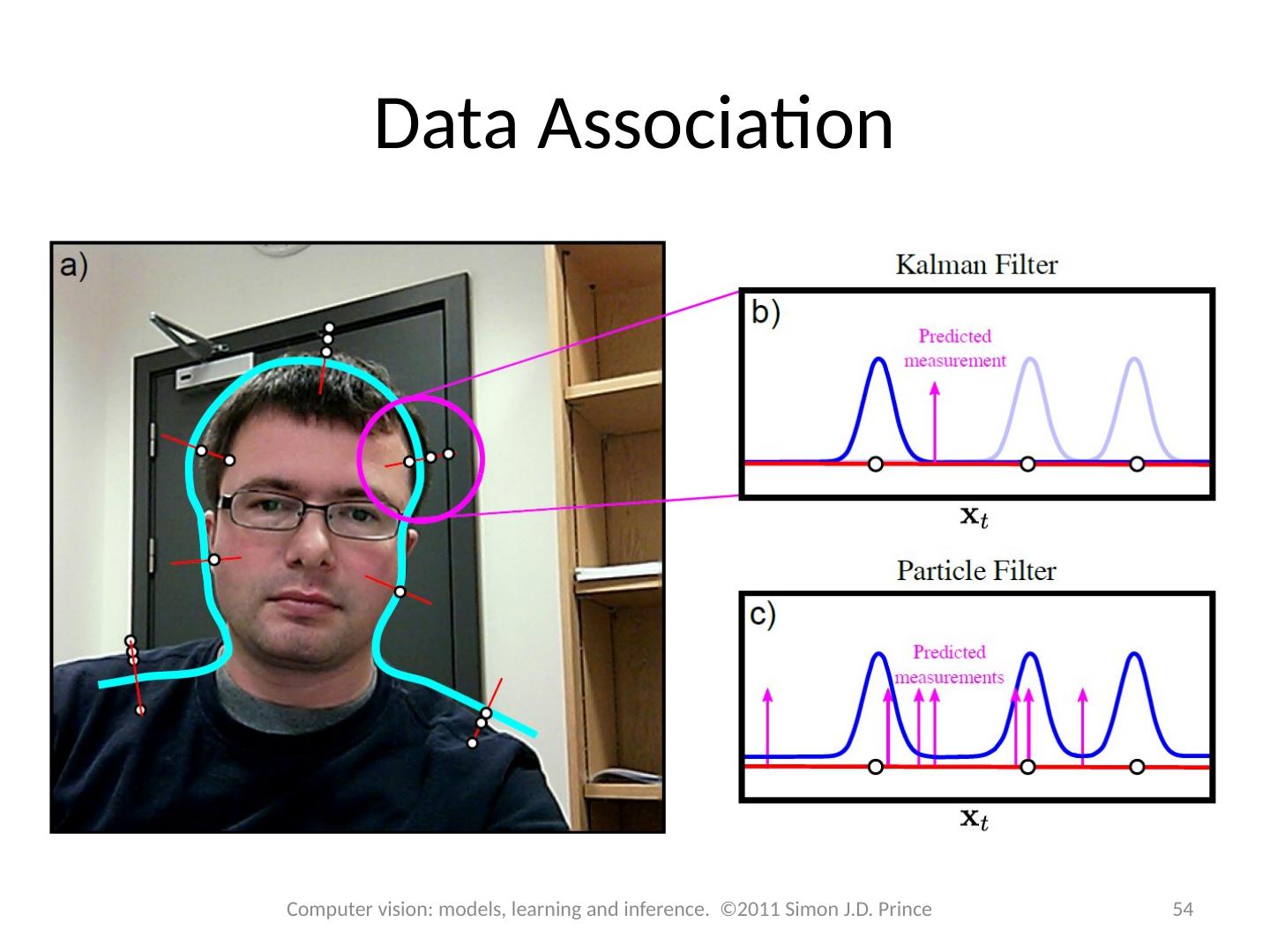
- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
19_Temporal_Models
展开查看详情
1 .Computer vision: models, learning and inference Chapter 19 Temporal models
2 .2
3 .Goal To track object state from frame to frame in a video Difficulties: Clutter (data association) One image may not be enough to fully define state Relationship between frames may be complicated
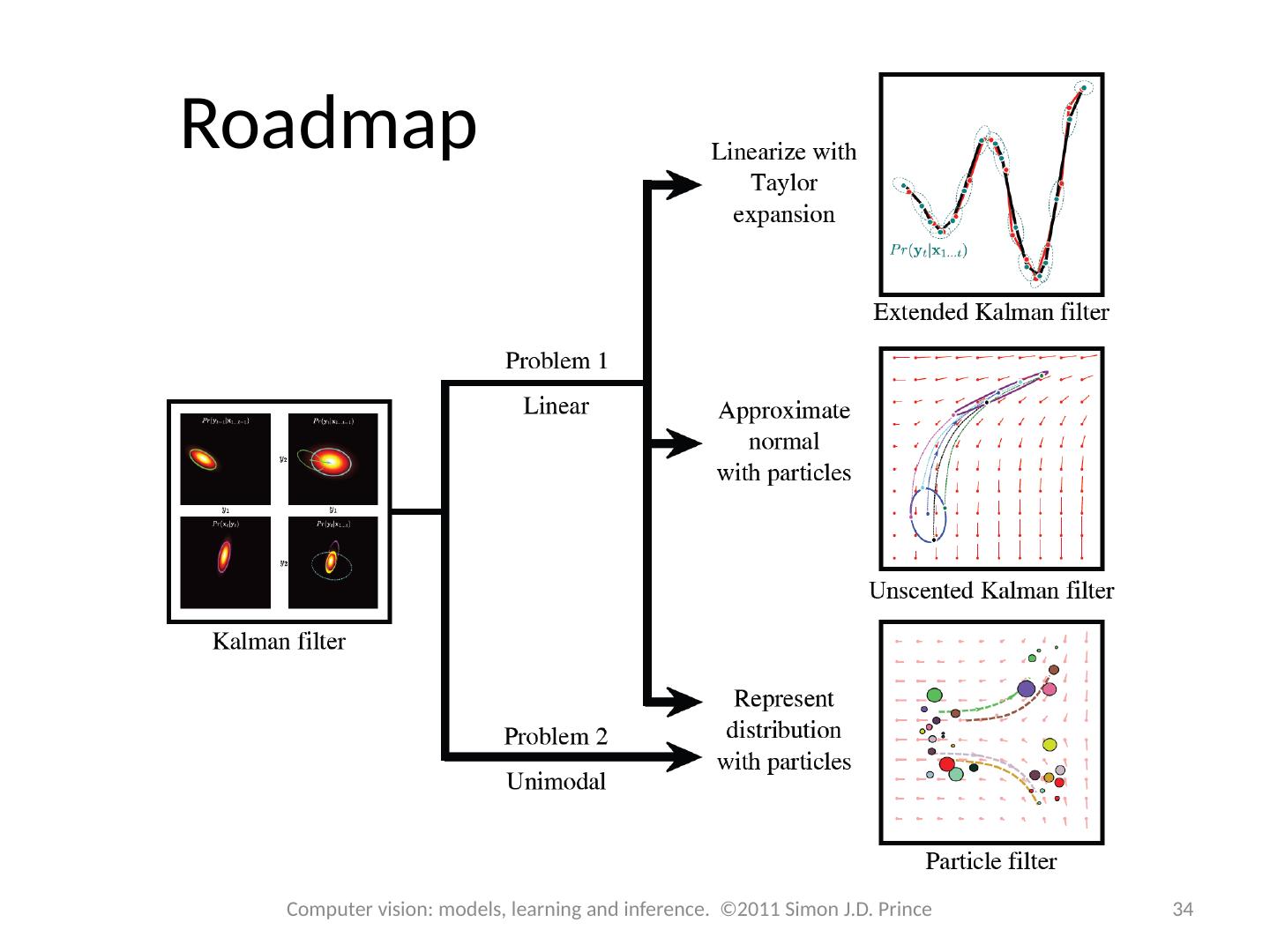
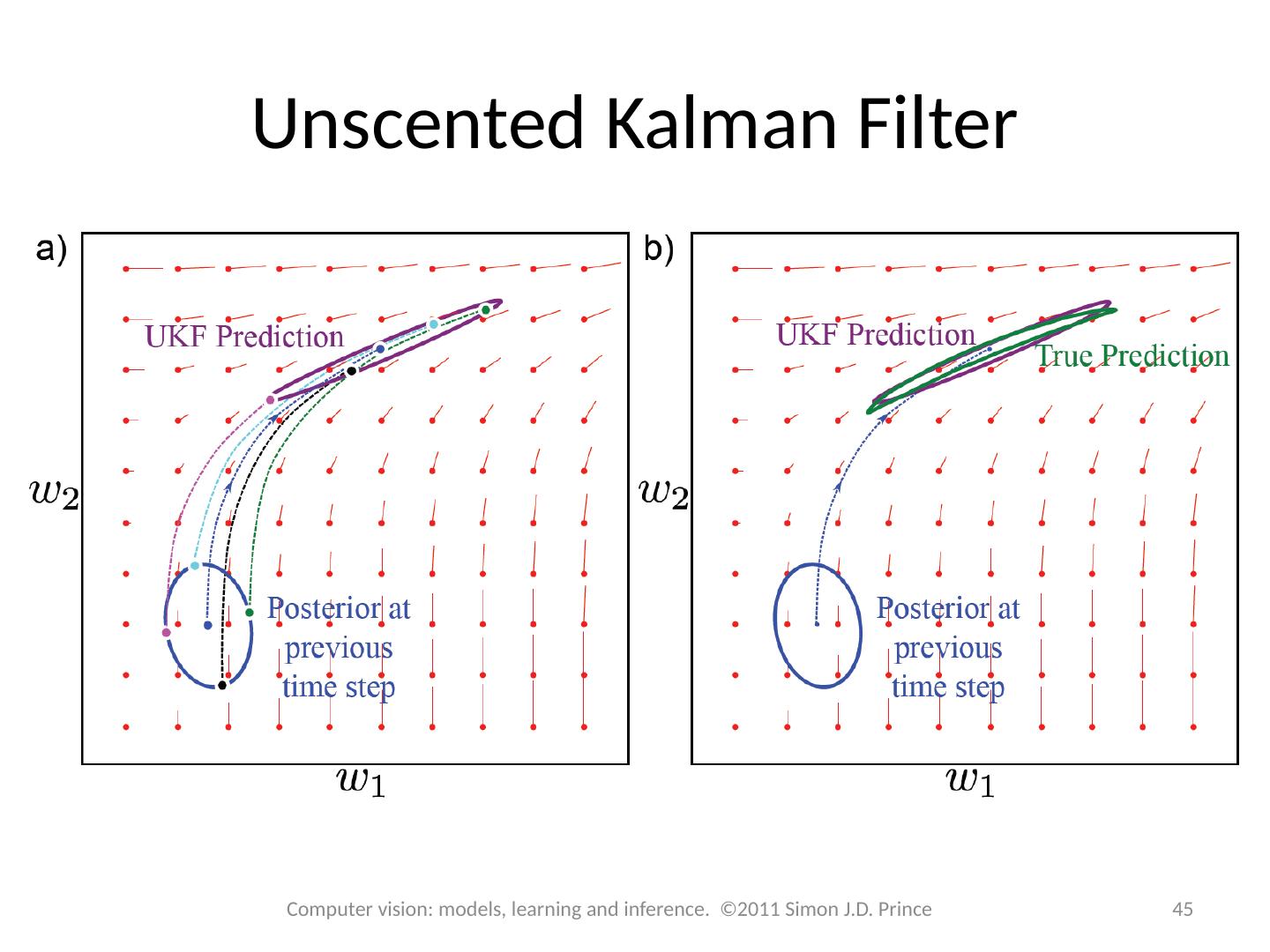
4 .Structure 4 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Temporal models Kalman filter Extended Kalman filter Unscented Kalman filter Particle filters Applications
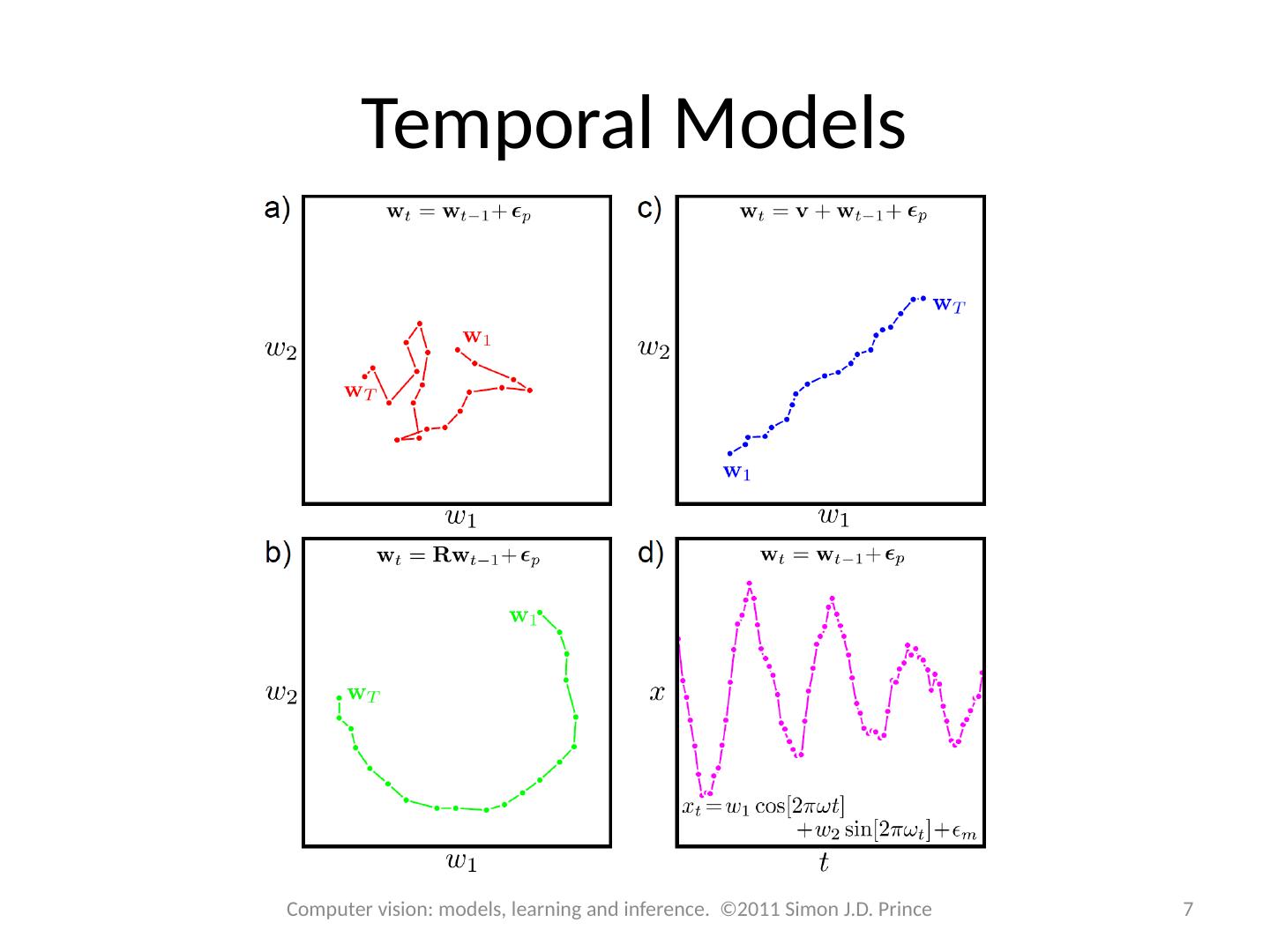
5 .5 Temporal Models Consider an evolving system Represented by an unknown vector, w This is termed the state Examples: 2D Position of tracked object in image 3D Pose of tracked object in world Joint positions of articulated model OUR GOAL: To compute the marginal posterior distribution over w at time t. 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
6 .6 Estimating State Two contributions to estimating the state: A set of measurements x t , which provide information about the state w t at time t. This is a generative model: the measurements are derived from the state using a known probability relation Pr( x t | w 1 … w T ) A time series model , which says something about the expected way that the system will evolve e.g., Pr( w t | w 1 ... w t-1 , w t+1 … w T ) 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
7 .Temporal Models 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
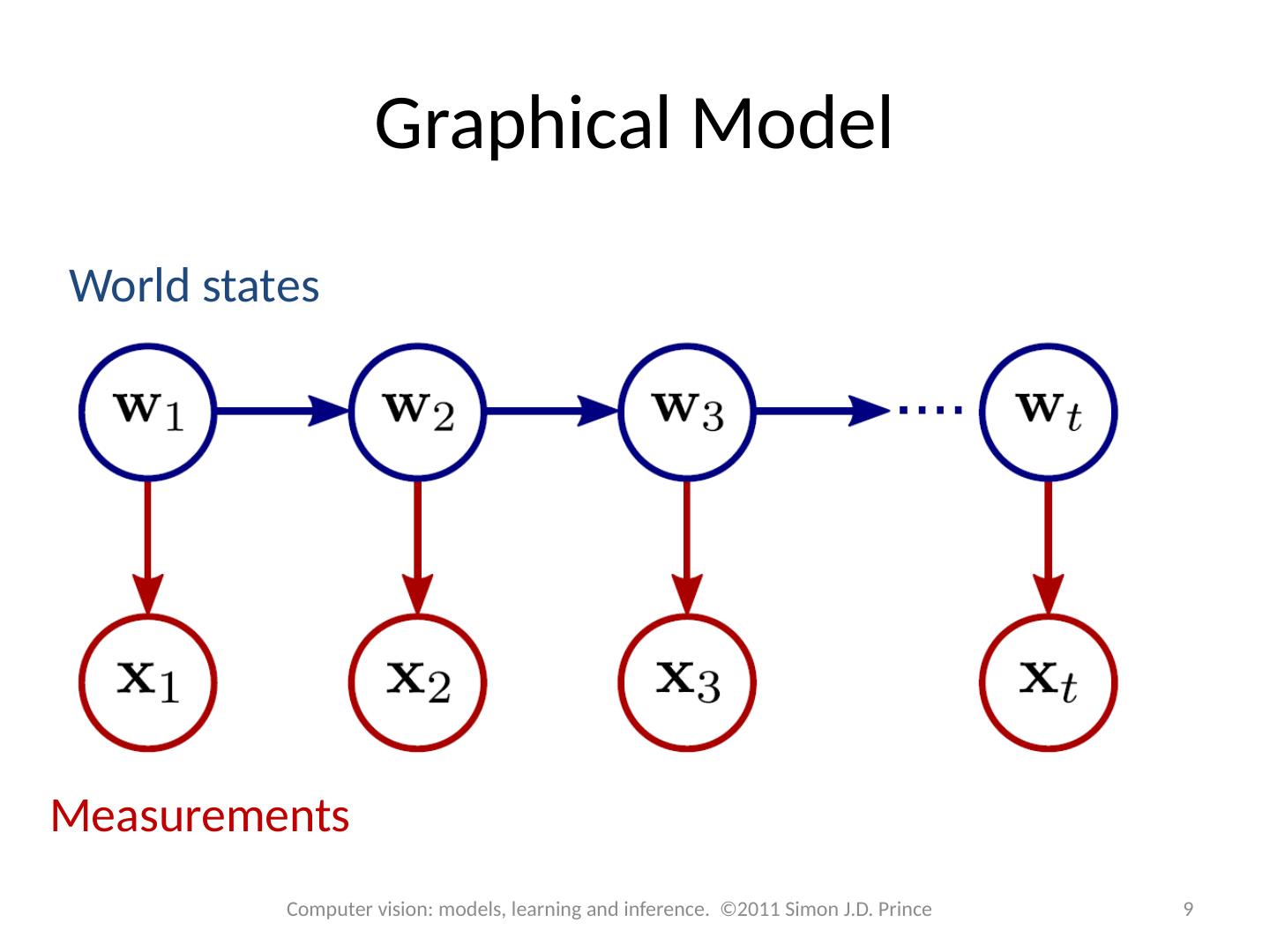
8 .Only the immediate past matters (Markov) the probability of the state at time t is conditionally independent of states at times 1...t-2 given the state at time t-1. Measurements depend on only the current state the likelihood of the measurements at time t is conditionally independent of all of the other measurements and the states at times 1...t-1, t+1..t given the state at time t. Assumptions 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
9 .Graphical Model World states Measurements 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
10 .Recursive Estimation Time 1 Time 2 Time t from temporal model 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
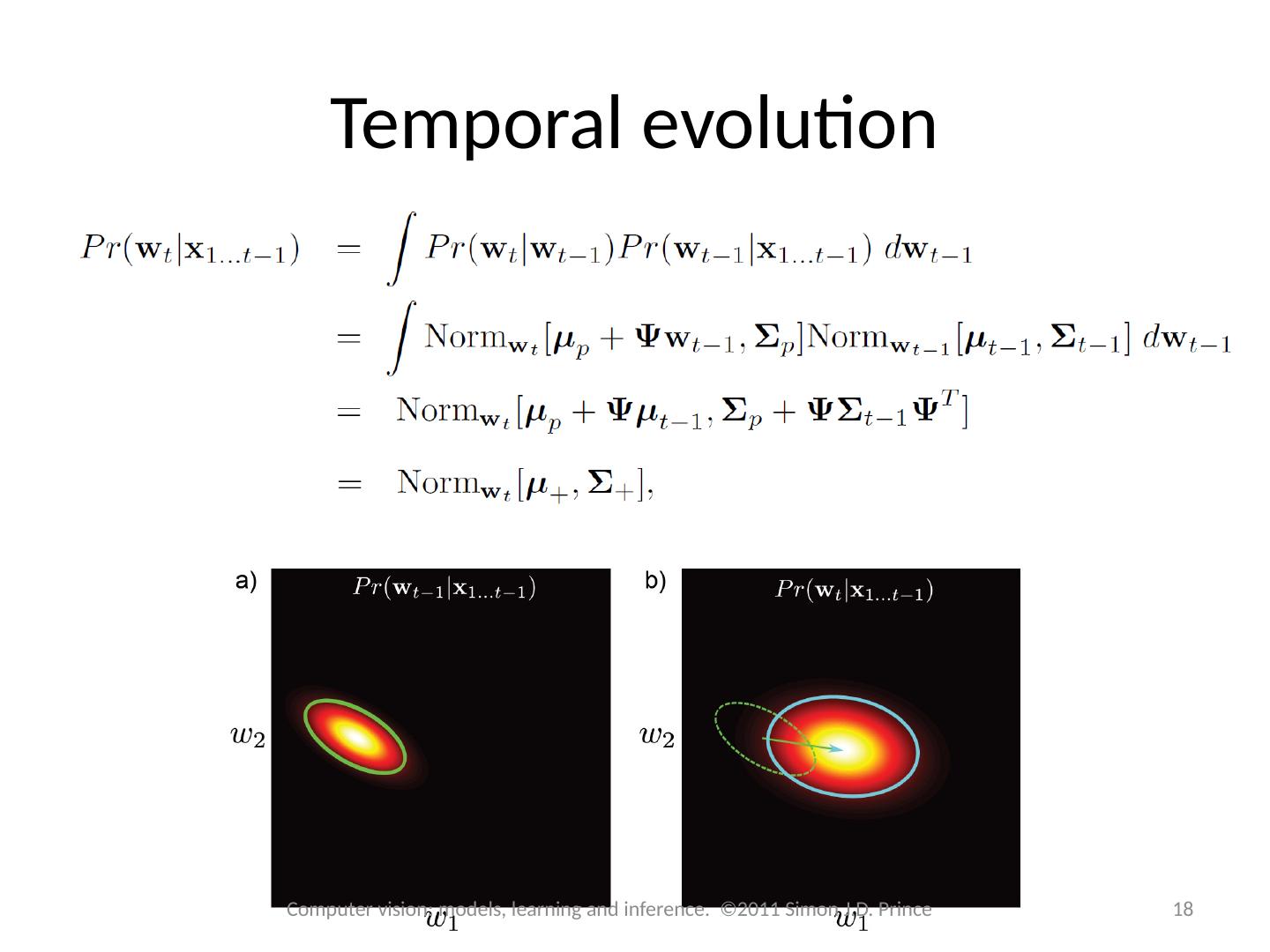
11 .Computing the prior (time evolution) Each time, the prior is based on the Chapman- Kolmogorov equation Prior at time t Temporal model Posterior at time t-1 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
12 .Summary Temporal Evolution Measurement Update Alternate between: Temporal model Measurement model 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
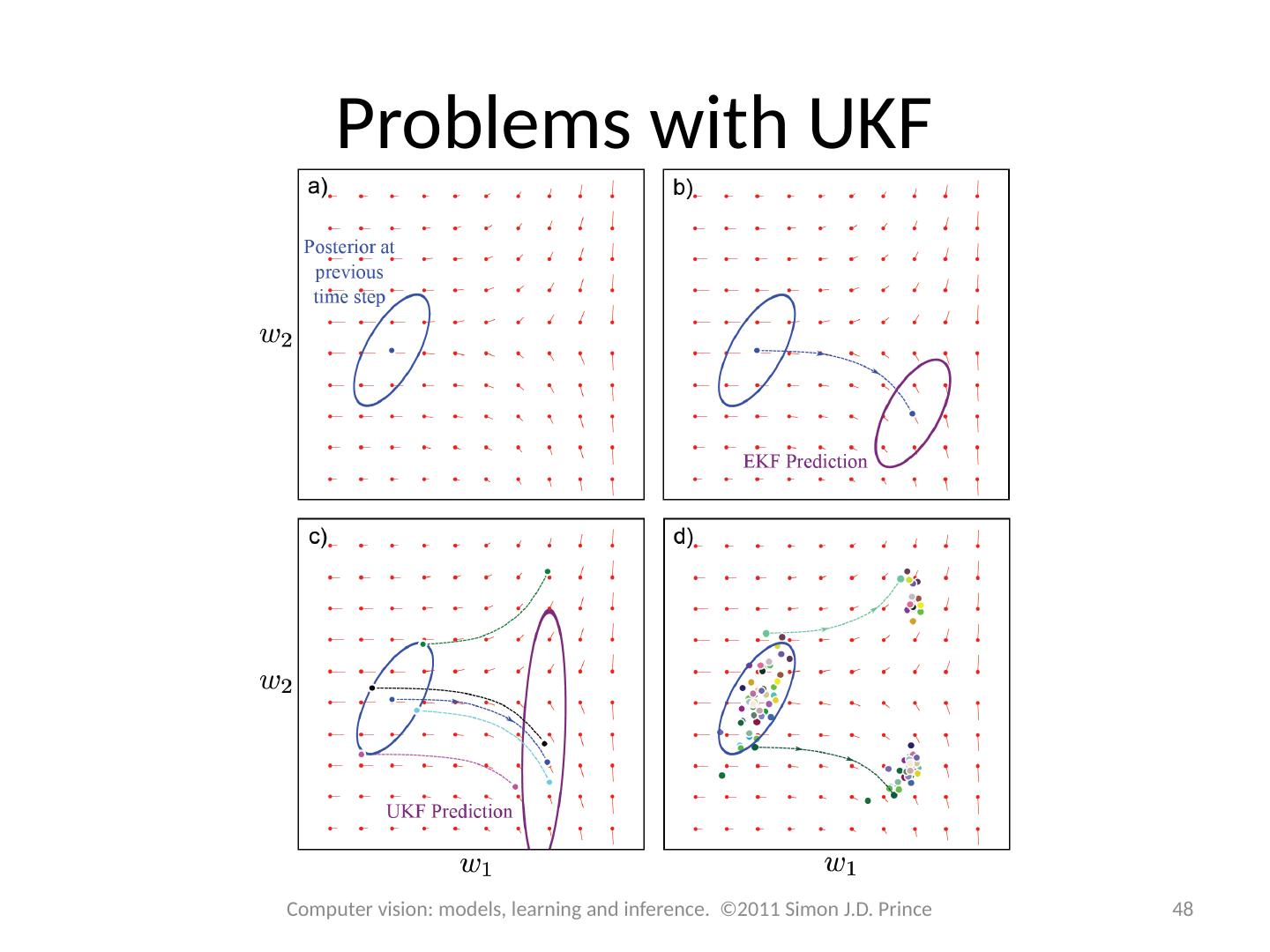
13 .Structure 13 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Temporal models Kalman filter Extended Kalman filter Unscented Kalman filter Particle filters Applications
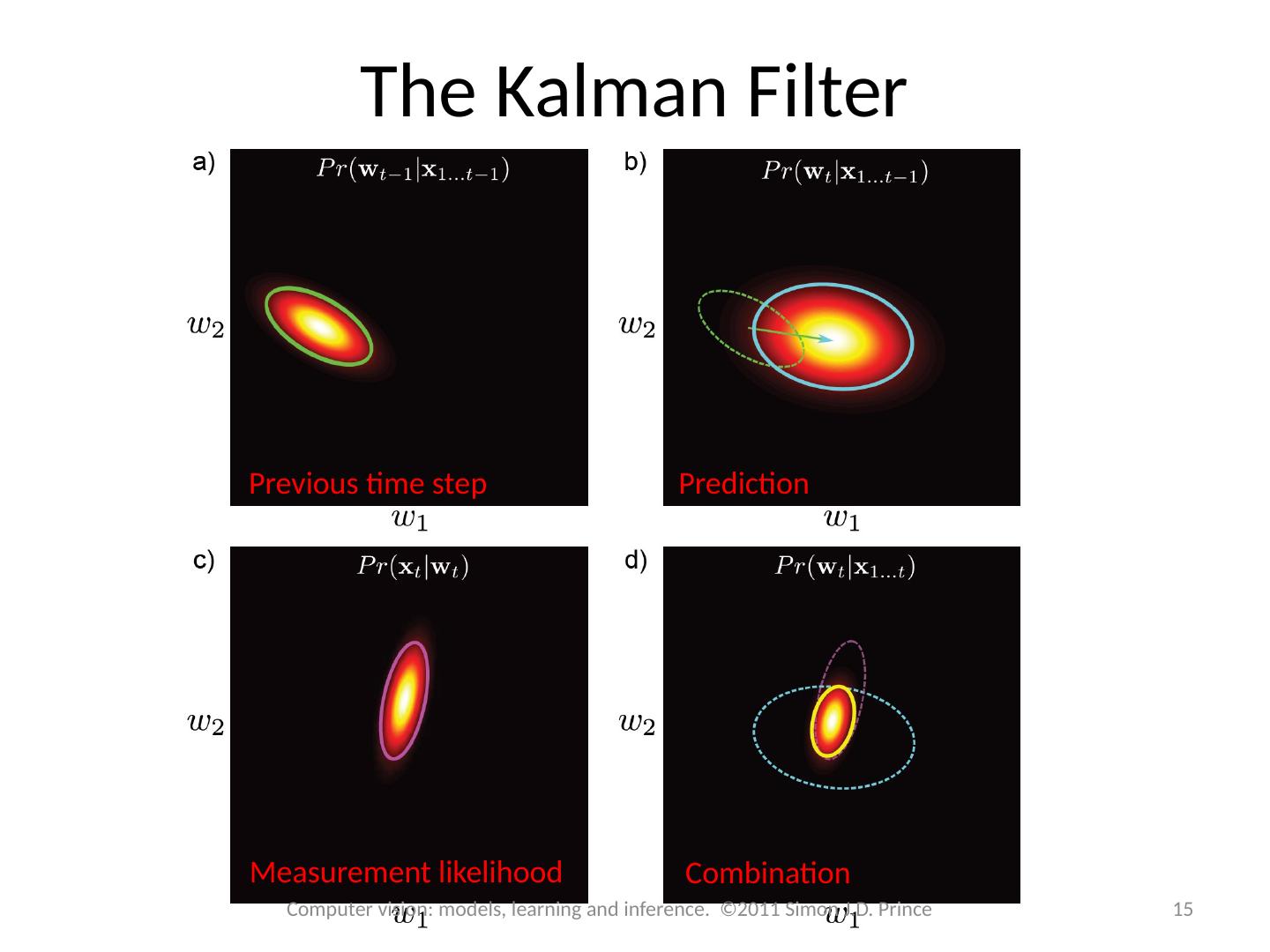
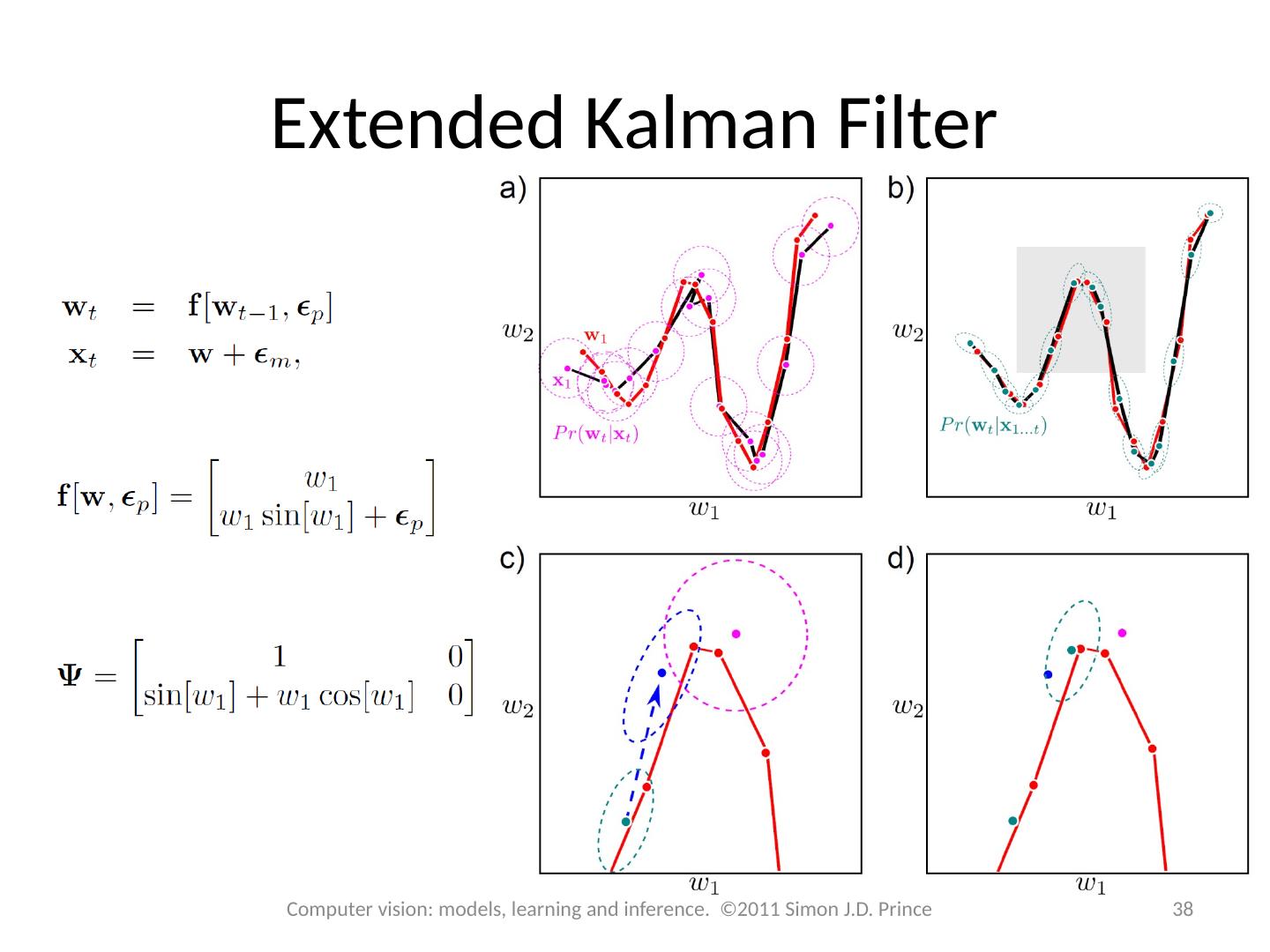
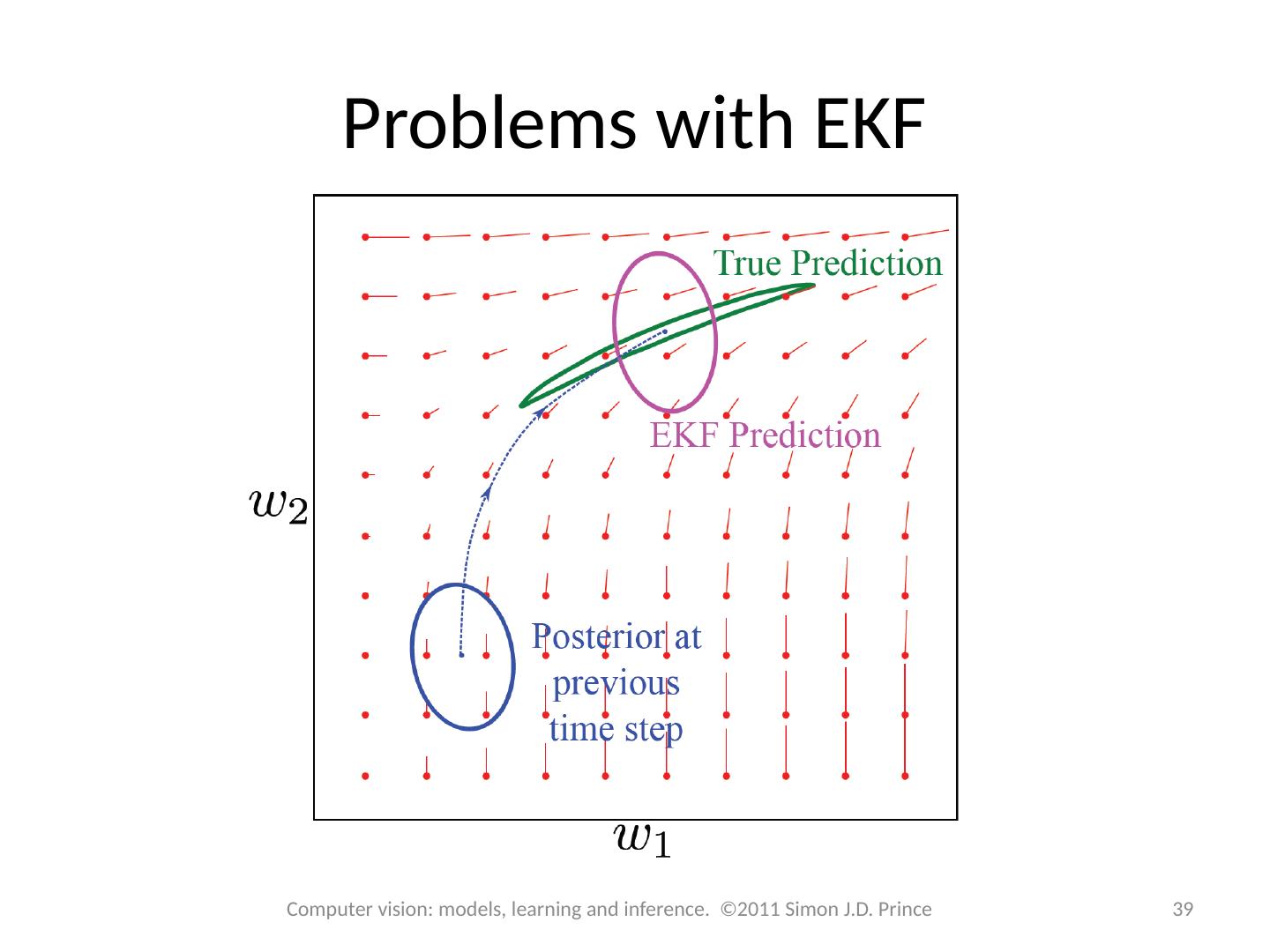
14 .Kalman Filter The Kalman filter is just a special case of this type of recursive estimation procedure. Temporal model and measurement model carefully chosen so that if the posterior at time t-1 was Gaussian then the prior at time t will be Gaussian posterior at time t will be Gaussian The Kalman filter equations are rules for updating the means and covariances of these Gaussians 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
15 .The Kalman Filter Previous time step Prediction Measurement likelihood Combination 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
16 .Kalman Filter Definition Time evolution equation Measurement equation State transition matrix Additive Gaussian noise Additive Gaussian noise Relates state and measurement 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
17 .Kalman Filter Definition Time evolution equation Measurment equation State transition matrix Additive Gaussian noise Additive Gaussian noise Relates state and measurement 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
18 .Temporal evolution 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
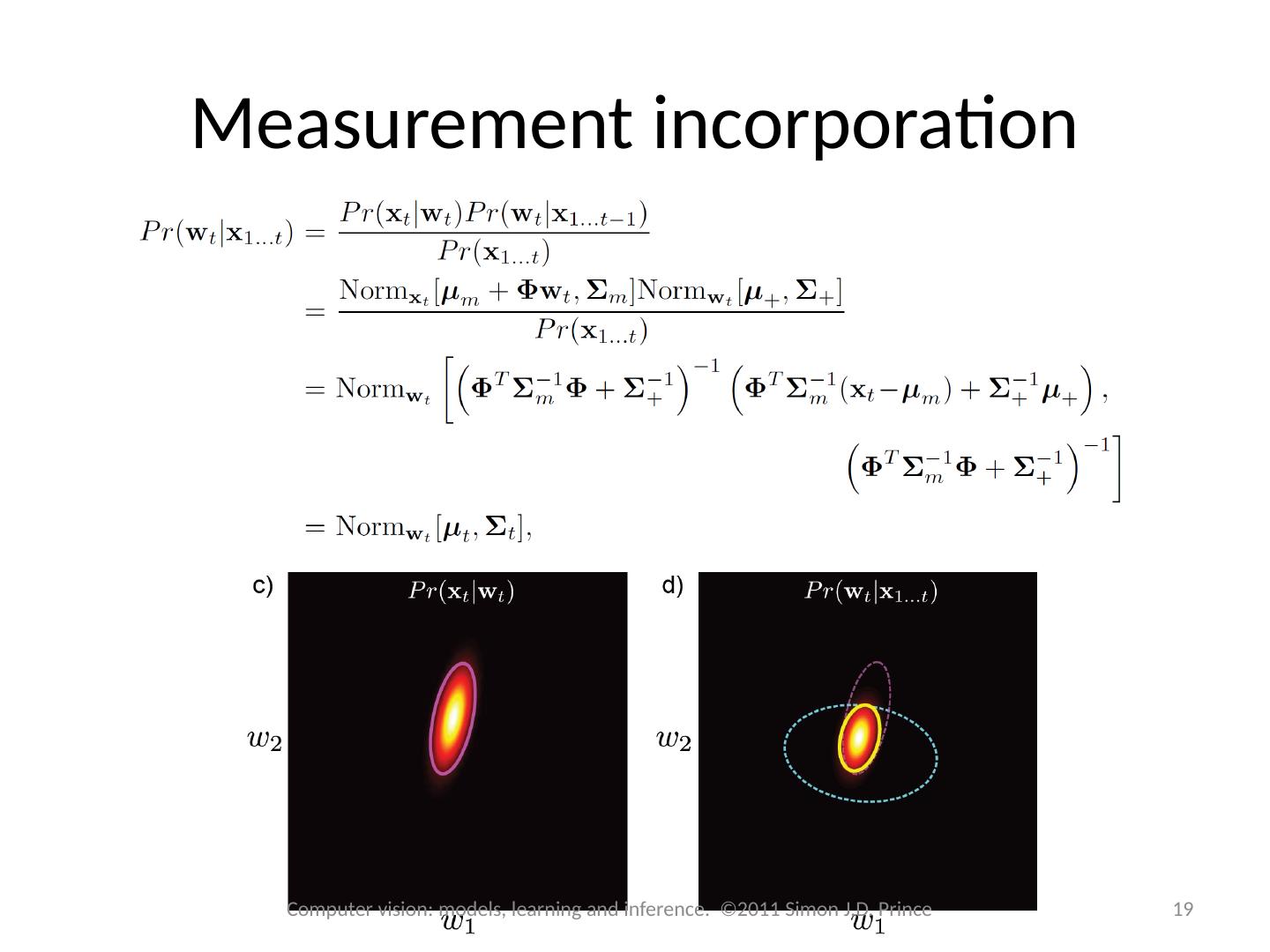
19 .Measurement incorporation 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
20 .Kalman Filter This is not the usual way these equations are presented. Part of the reason for this is the size of the inverses: f is usually landscape and so f T f is inefficient Define Kalman gain: 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
21 .Mean Term Using Matrix inversion relations: 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
22 .Covariance Term Kalman Filter Using Matrix inversion relations: 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
23 .Final Kalman Filter Equation Innovation (difference between actual and predicted measurements Prior variance minus a term due to information from measurement 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
24 .Kalman Filter Summary Time evolution equation Measurement equation Inference 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
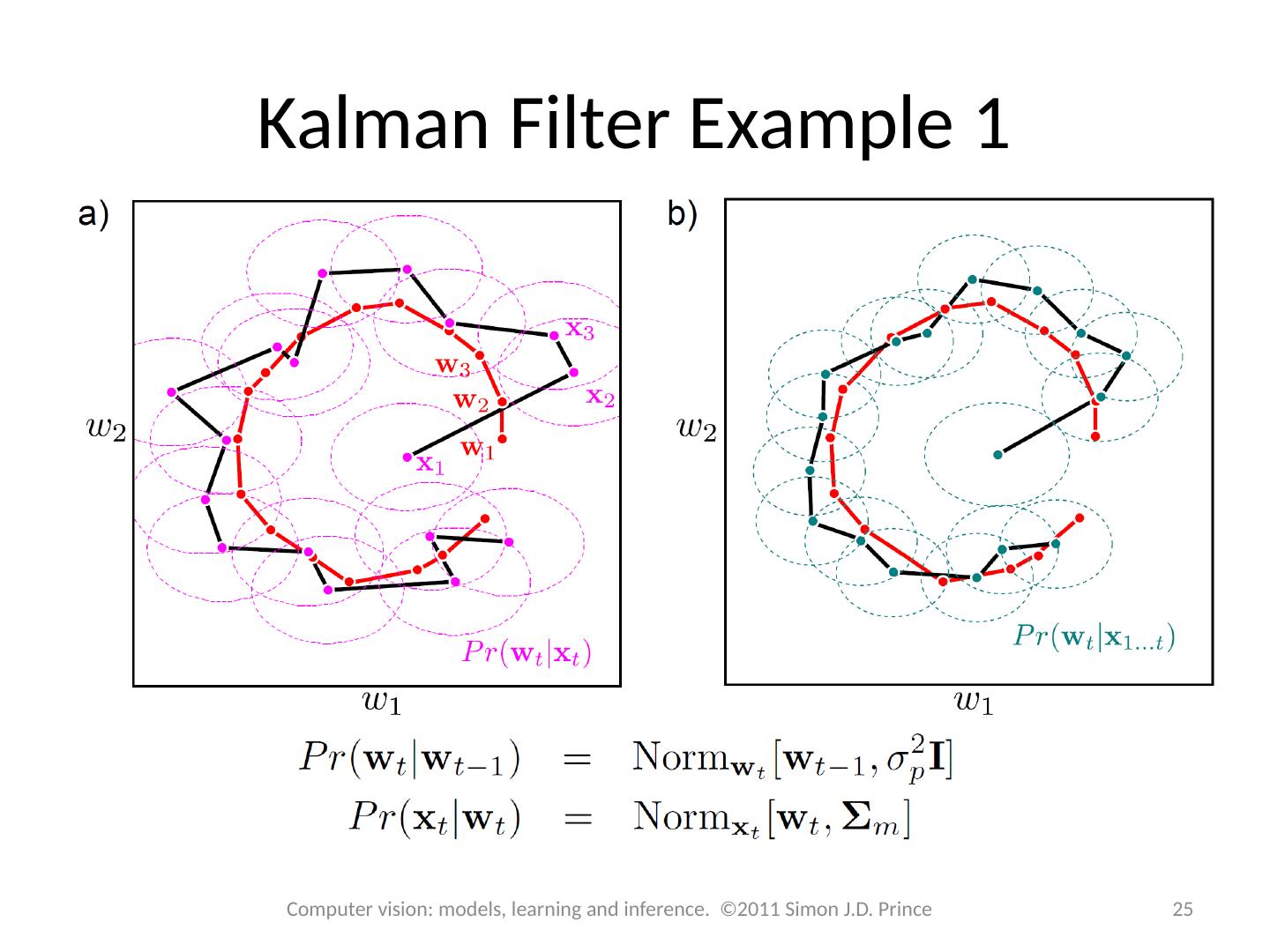
25 .Kalman Filter Example 1 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
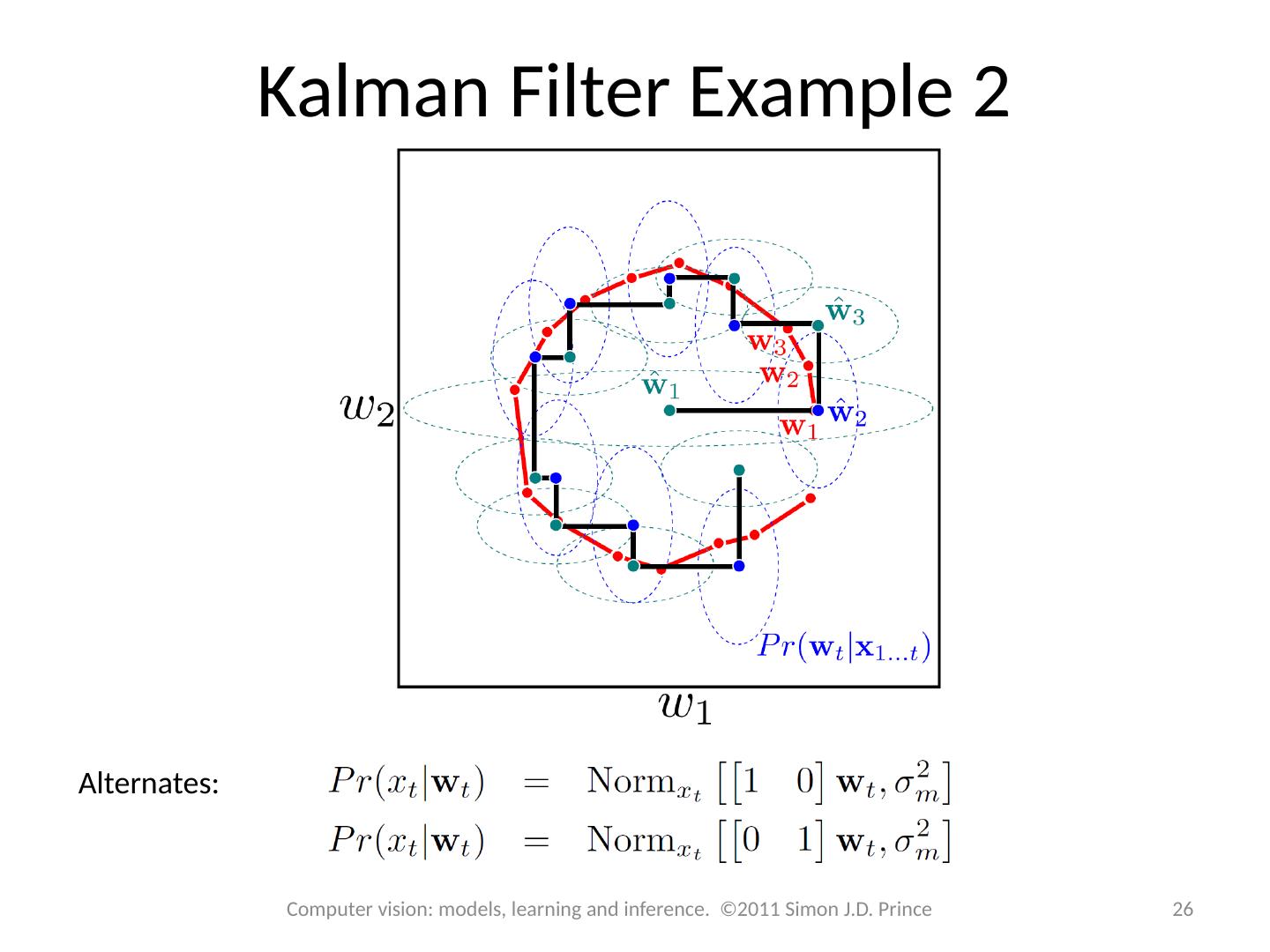
26 .Kalman Filter Example 2 Alternates: 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
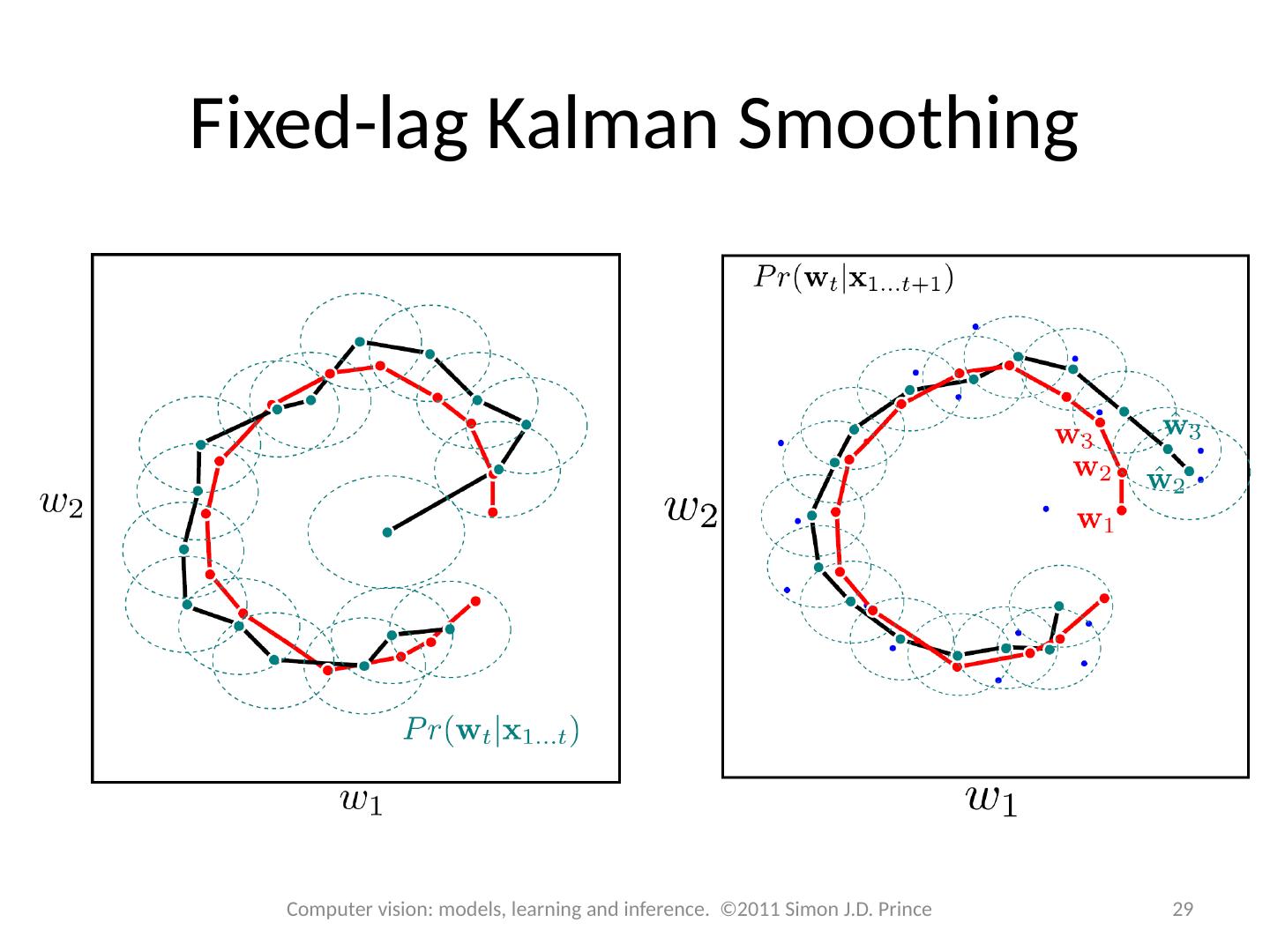
27 .27 Smoothing Estimates depend only on measurements up to the current point in time . Sometimes want to estimate state based on future measurements as well Fixed Lag Smoother : This is an on-line scheme in which the optimal estimate for a state at time t -t is calculated based on measurements up to time t , where t is the time lag. i.e. we wish to calculate Pr ( w t - t |x 1 . . . x t ). Fixed Interval Smoother : We have a fixed time interval of measurements and want to calculate the optimal state estimate based on all of these measurements. In other words , instead of calculating Pr ( w t |x 1 . . . x t ) we now estimate Pr (w t |x 1 . . . x T ) where T is the total length of the interval. 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
28 .28 Fixed lag smoother 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince State evolution equation Measurement equation Estimate delayed by t
29 .Fixed-lag Kalman Smoothing 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince