17_Models_For_Shape

1 .Computer vision: models, learning and inference Chapter 17 Models for shape

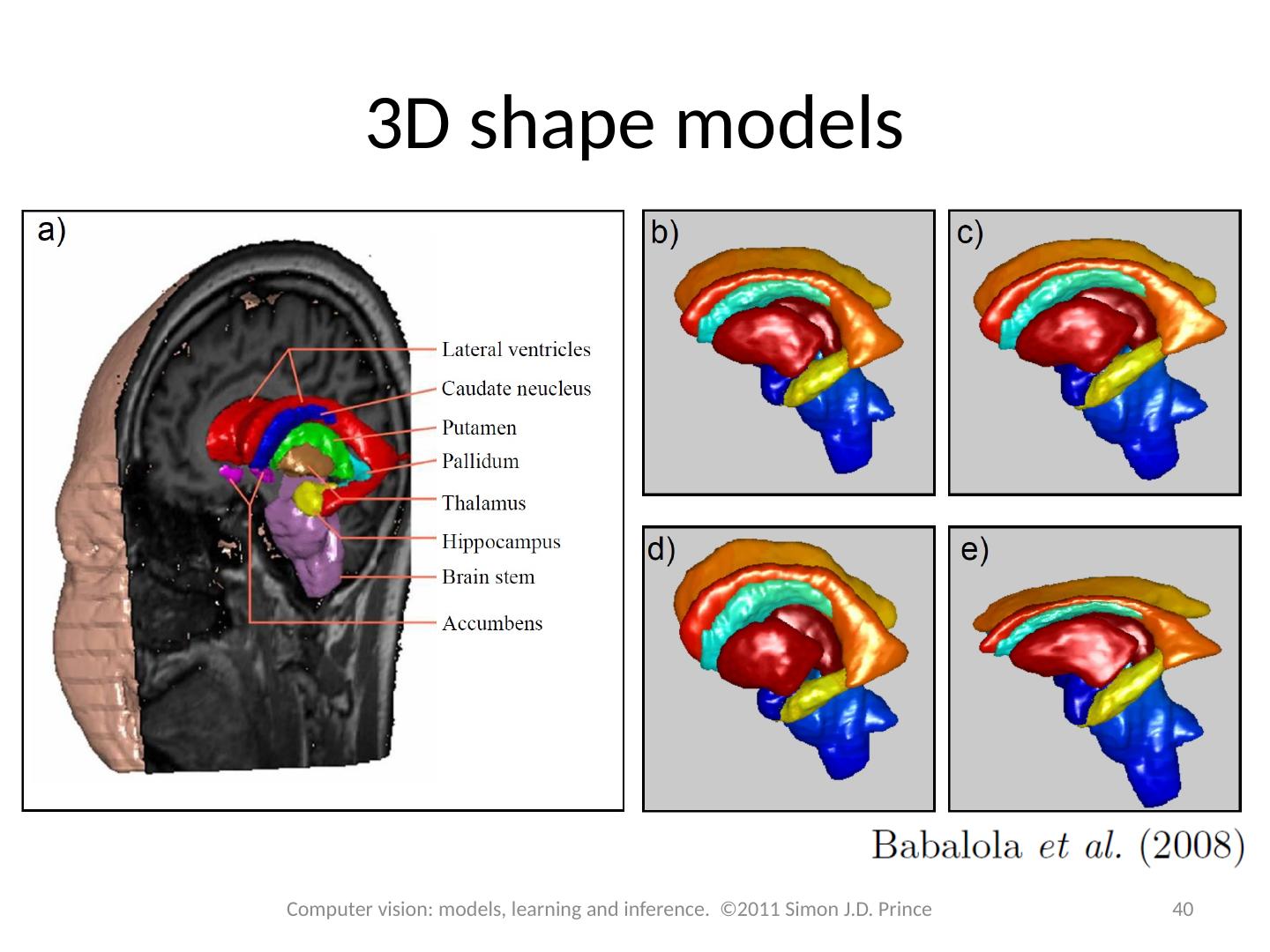
2 .Structure 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Snakes Template models Statistical shape models 3D shape models Models for shape and appearance Non-linear models Articulated models Applications

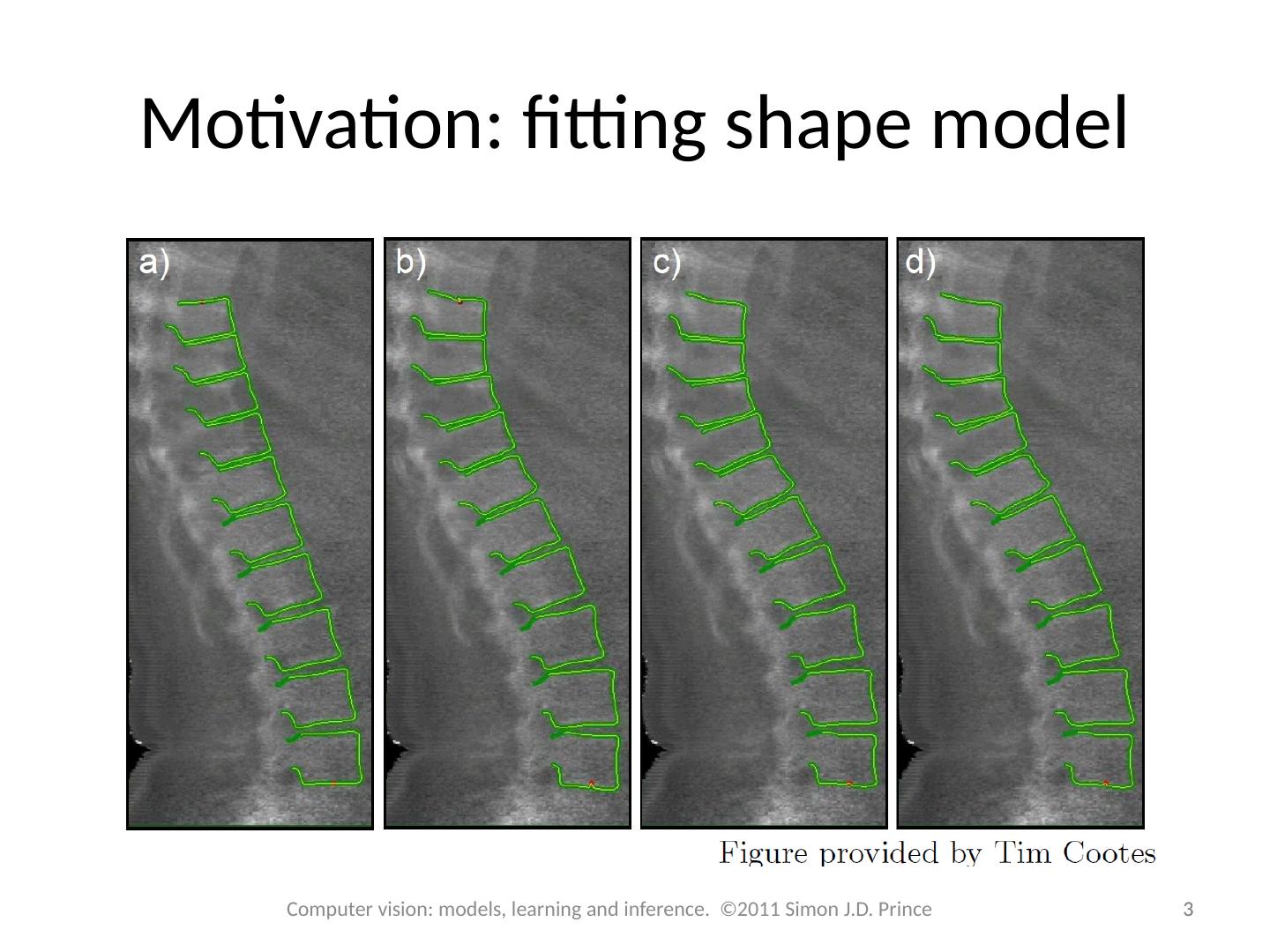
3 .Motivation: fitting shape model 3 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

4 .What is shape? Kendall (1984) – Shape “is all the geometrical information that remains when location scale and rotational effects are filtered out from an object” In other words, it is whatever is invariant to a similarity transformation 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

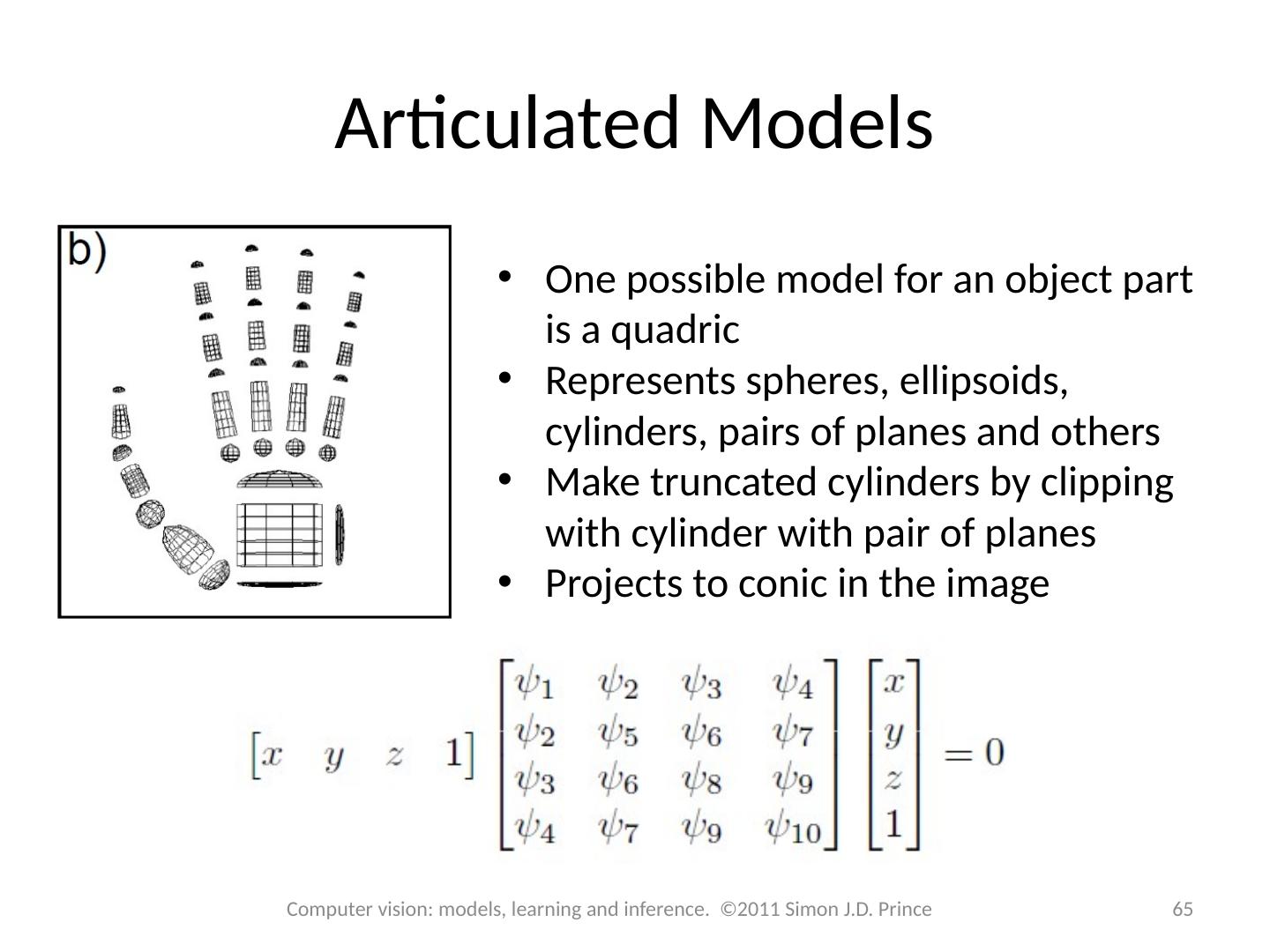
5 .Representing Shape Algebraic modelling Line: Conic: More complex objects? Not practical for spine. 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

6 .Landmark Points 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Landmark points can be thought of as discrete samples from underlying contour Ordered (single continuous contour) Ordered with wrapping (closed contour) More complex organisation (collection of closed and open)

7 .Snakes Provide only weak information: contour is smooth Represent contour as N 2D landmark points We will construct terms for The likelihood of observing an image x given landmark points W . Encourages landmark points to lie on border in the image The prior of the landmark point. Encourages the contours to be smooth. 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

8 .Snakes 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Initialise contour and let it evolve until it grabs onto an object Crawls across the image – hence called snake or active contour

9 .Snake likelihood 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Has correct properties (probability high at edges), but flat in regions distant from the contour. Not good for optimisation.

10 .Snake likelihood (2) 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Compute edges (here using Canny) and then compute distance image – this varies smoothly with distance from the image

11 .Prior Encourages smoothness Encourages equal spacing Encourages low curvature 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

12 .Inference Maximise posterior probability No closed form solution Must use non-linear optimisation method Number of unknowns = 2N 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

13 .Snakes 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Notice failure at nose – falls between points. A better model would sample image between landmark points

14 .Inference Maximise posterior probability Very slow. Can potentially speed it up by changing spacing element of prior: Take advantage of limited connectivity of associated graphical model 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

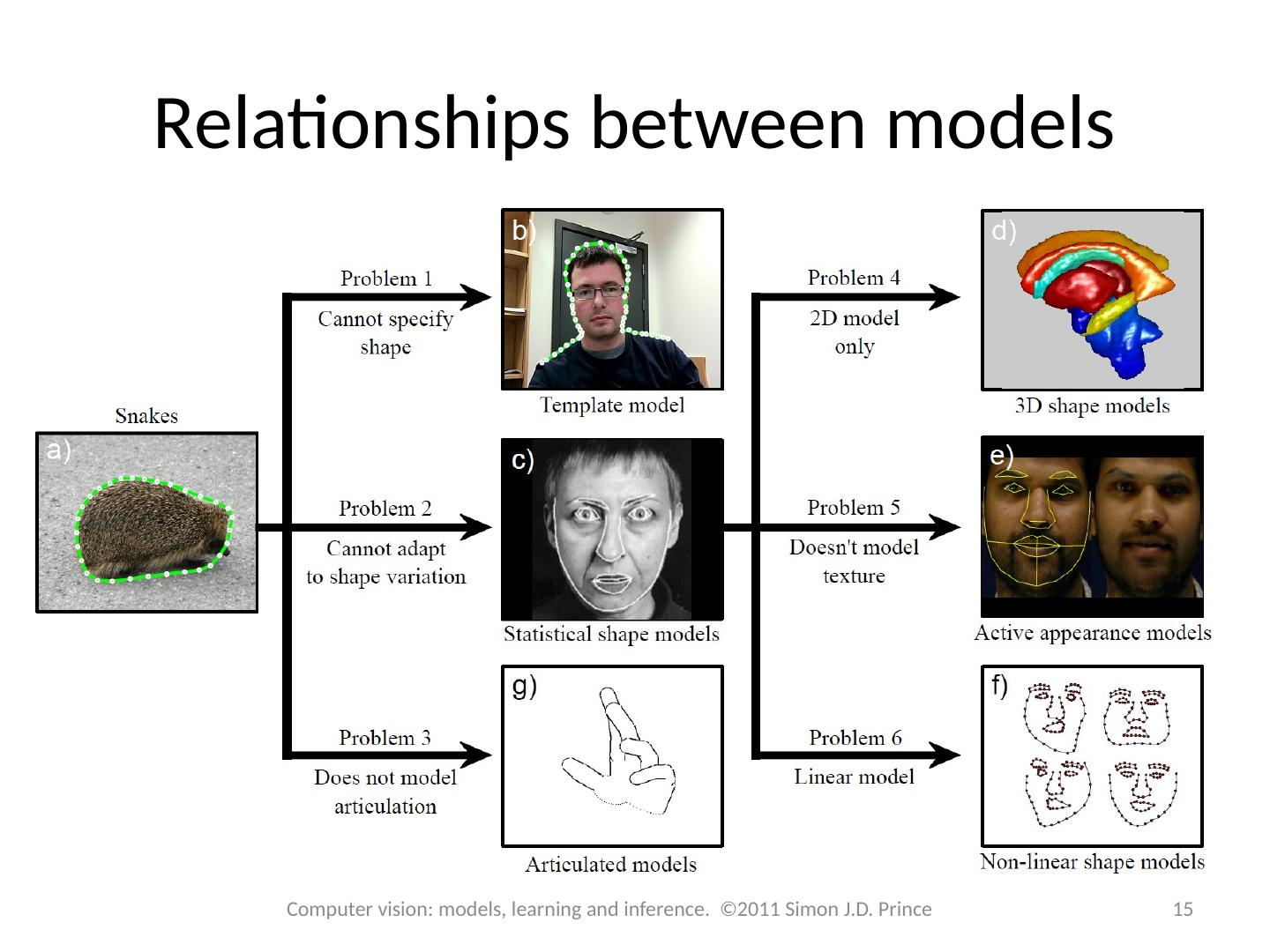
15 .Relationships between models 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

16 .Structure 16 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Snakes Template models Statistical shape models 3D shape models Models for shape and appearance Non-linear models Articulated models Applications

17 .Shape template model Shape based on landmark points These points are assumed known Mapped into the image by transformation What is left is to find parameters of transformation Likelihood is based on distance transform: No prior on parameters (but could have one) 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

18 .Shape template model 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

19 .Inference Use maximum likelihood approach No closed form solution Must use non-linear optimization Use chain rule to compute derivatives 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

20 .Iterative closest points 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Find nearest edge point to each landmark point Compute transformation in closed form Repeat

21 .Structure 21 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Snakes Template models Statistical shape models 3D shape models Models for shape and appearance Non-linear models Articulated models Applications

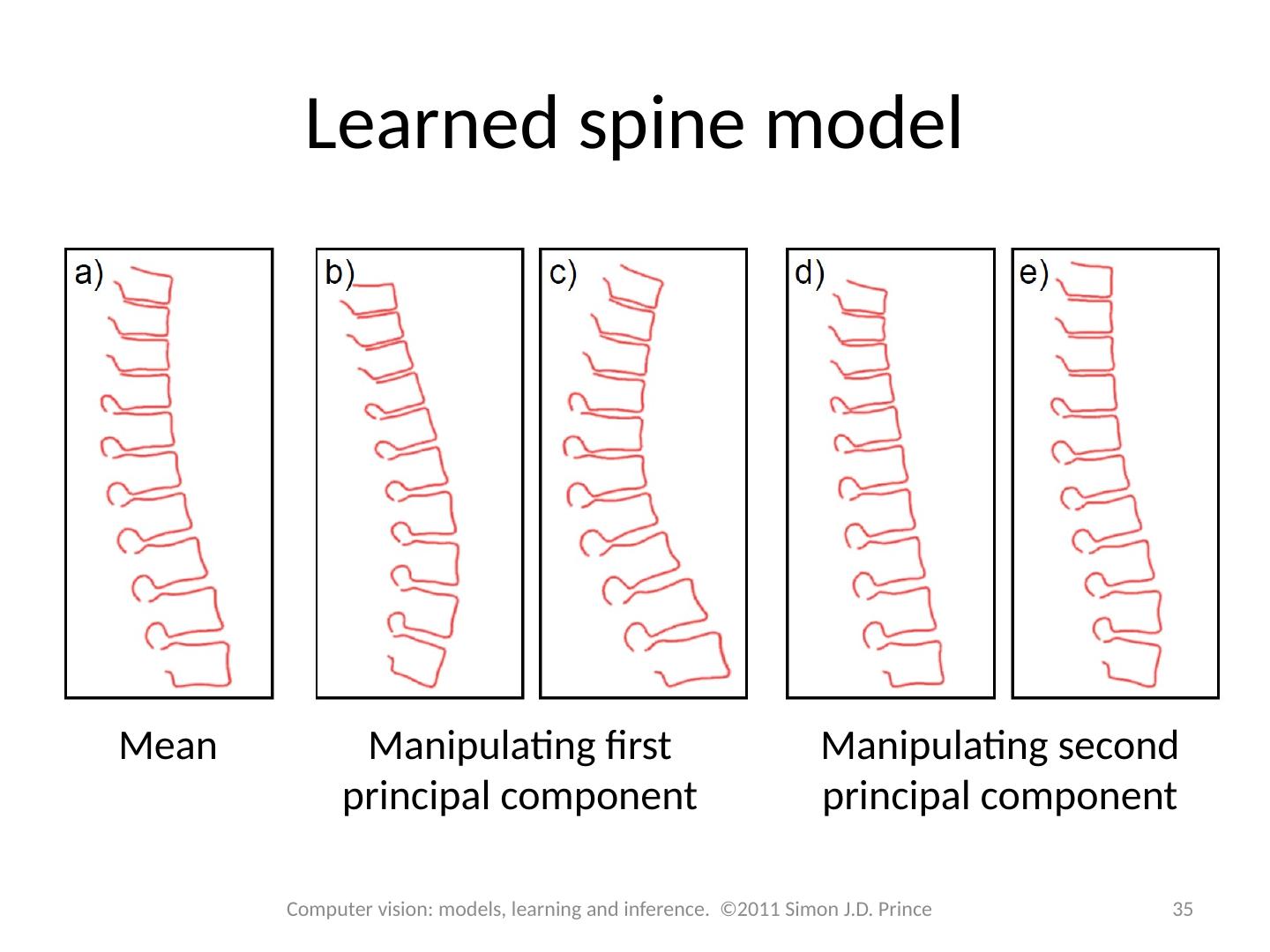
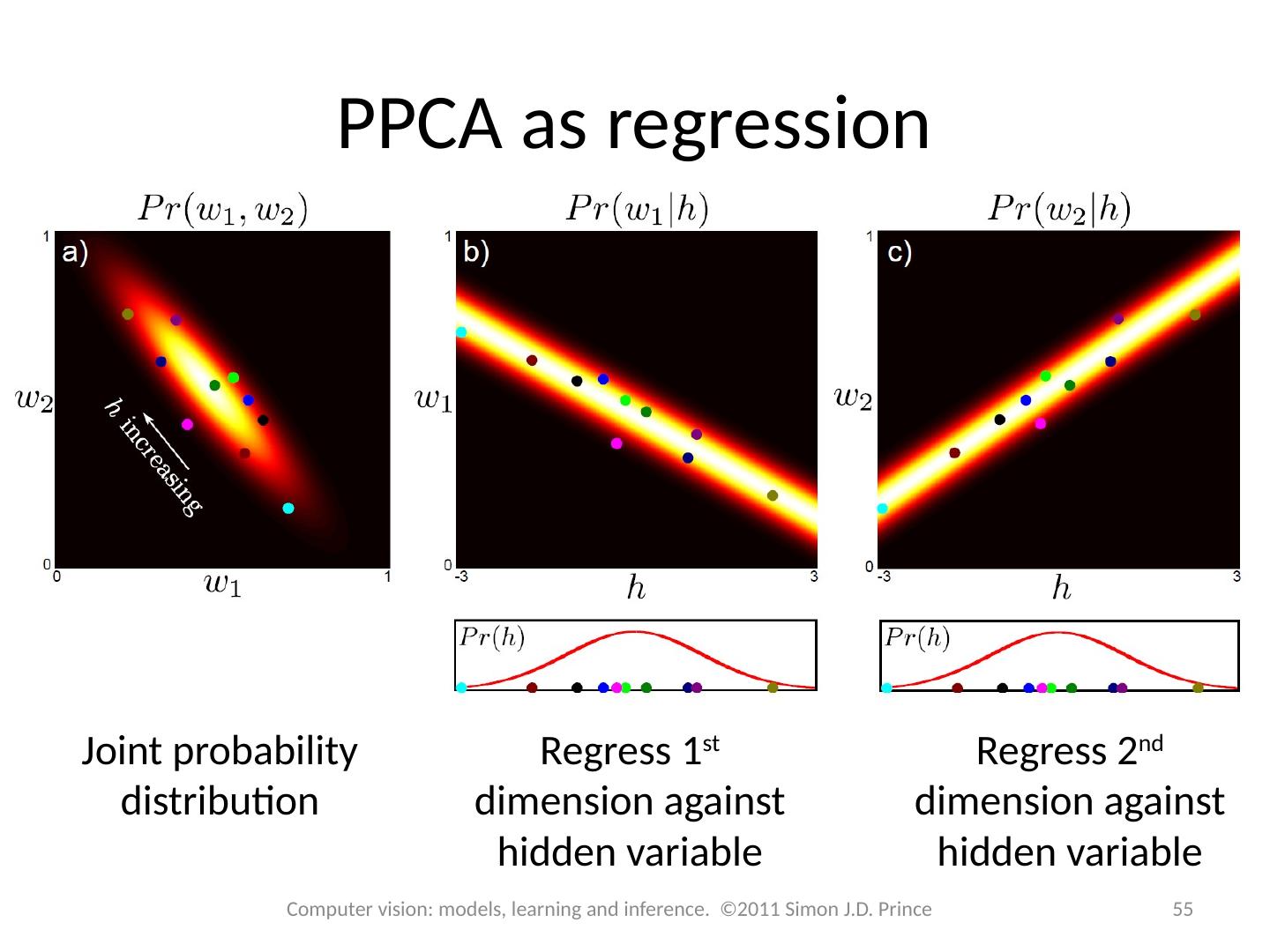
22 .Statistical shape models Also called Point distribution models Active shape models (as they adapt to the image) Likelihood: Prior: 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

23 .Learning Usually, we are given the examples after they have been transformed Before we can learn the normal distribution, we must compute the inverse transformation Procedure is called generalized Procrustes analysis 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

24 .Generalized Procrustes analysis 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Training data Before alignment After alignment

25 .Generalized Procrustes analysis Alternately Update all transformations to map landmark points to current mean Update mean to be average of transformed values, Then learn mean and variance parameters. 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

26 .Inference Map inference: No closed form solution Use non-linear optimisation Or use ICP approach However, many parameters, and not clear they are all needed more efficient to use subspace model 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

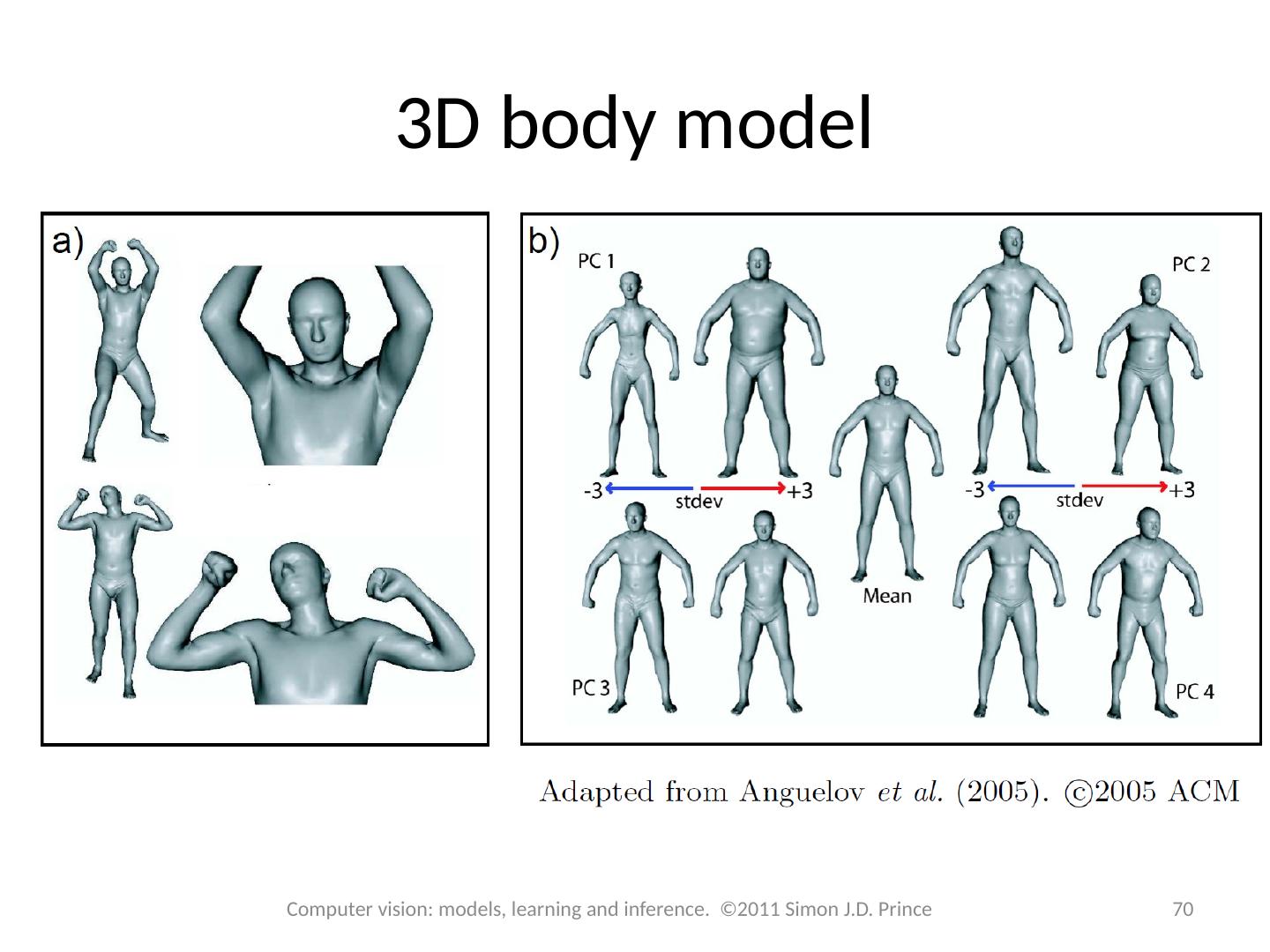
27 .Face model 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Three samples from learned model for faces

28 .Subspace shape model Generate data from model: is the mean shape the matrix contains K basis functions in it columns is normal noise with covariance Can alternatively write 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

29 .Approximating with subspace 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Subspace model Can approximate an vector w with a weighted sum of the basis functions Surprising how well this works even with a small number of basis functions