16_Multiple_Cameras

1 .Computer vision: models, learning and inference Chapter 16 Multiple Cameras

2 .Structure from motion 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Given an object that can be characterized by I 3D points projections into J images Find Intrinsic matrix Extrinsic matrix for each of J images 3D points

3 .Structure from motion 3 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince For simplicity, we’ll start with simpler problem Just J=2 images Known intrinsic matrix

4 .Structure 4 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Two view geometry The essential and fundamental matrices Reconstruction pipeline Rectification Multi-view reconstruction Applications

5 .Epipolar lines 5 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

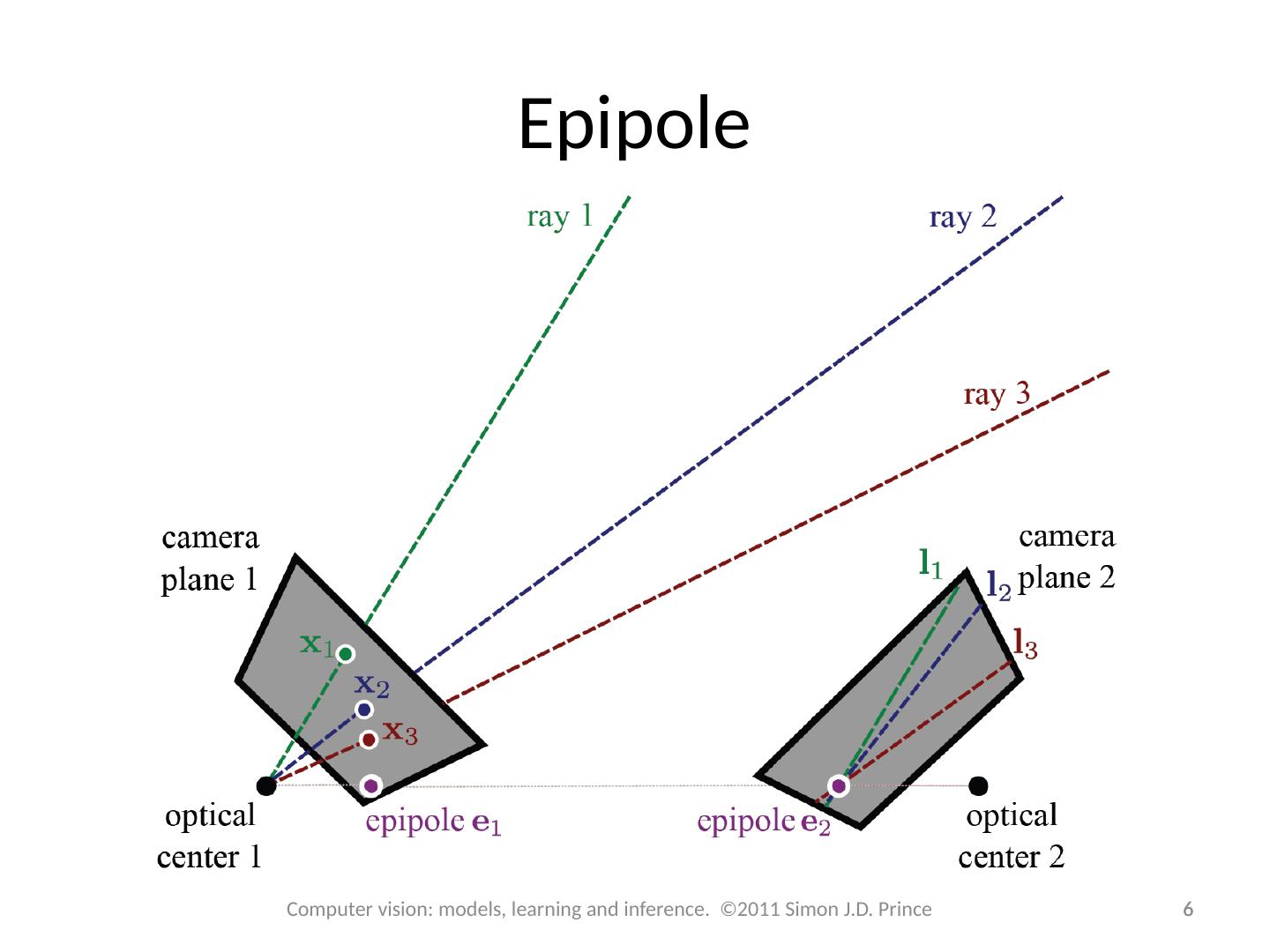
6 .Epipole 6 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

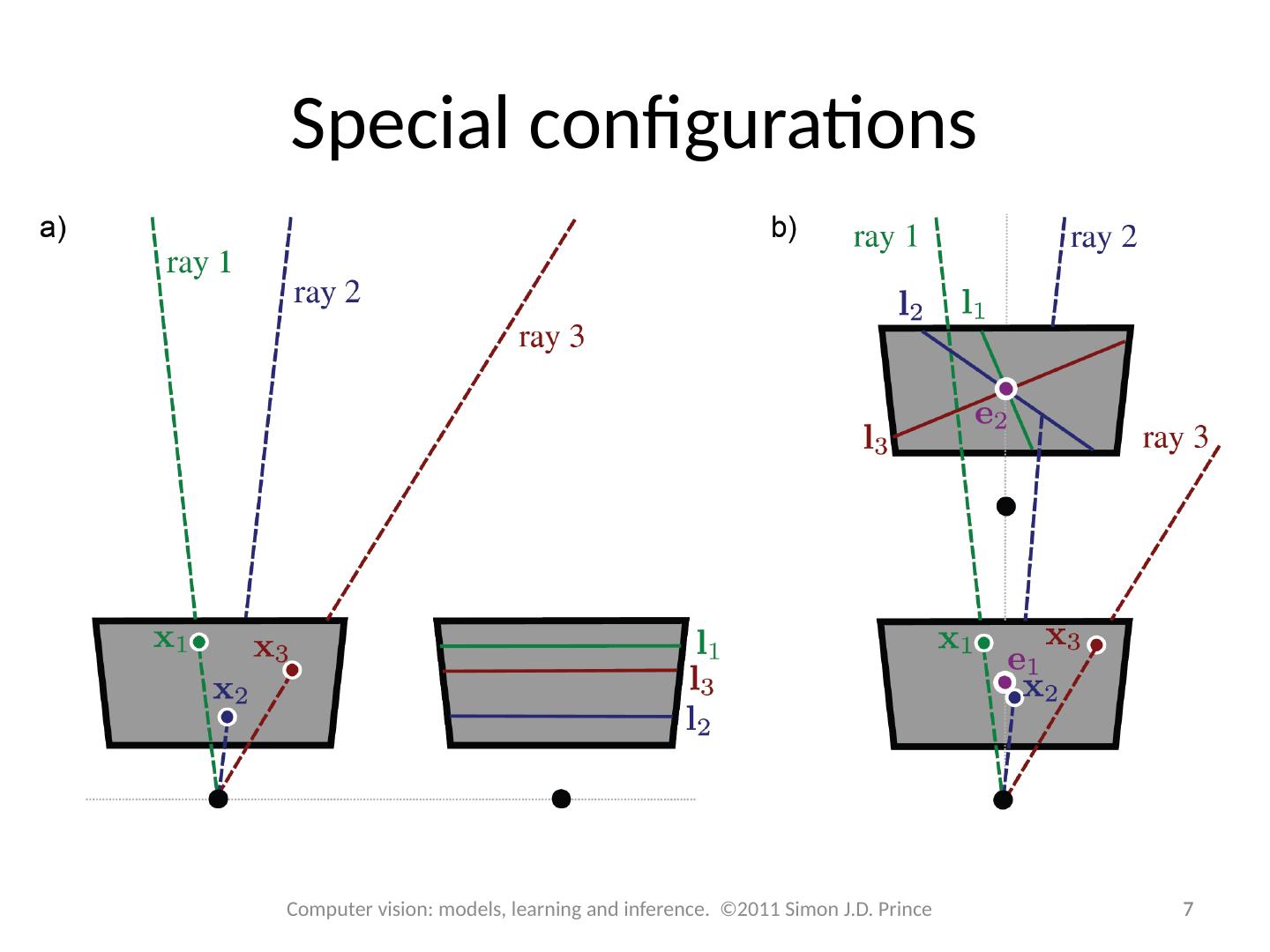
7 .Special configurations 7 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

8 .Structure 8 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Two view geometry The essential and fundamental matrices Reconstruction pipeline Rectification Multi-view reconstruction Applications

9 .The geometric relationship between the two cameras is captured by the essential matrix. Assume normalized cameras, first camera at origin. First camera: Second camera: The essential matrix 9 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

10 .The essential matrix 10 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince First camera: Second camera: Substituting: This is a mathematical relationship between the points in the two images, but it’s not in the most convenient form.

11 .The essential matrix 11 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Take cross product with t (last term disappears) Take inner product of both sides with x 2 .

12 .The cross product term can be expressed as a matrix Defining: We now have the essential matrix relation The essential matrix 12 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

13 .Properties of the essential matrix 13 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Rank 2: 5 degrees of freedom Non-linear constraints between elements

14 .Recovering epipolar lines 14 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Equation of a line: or or

15 .Recovering epipolar lines 15 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Equation of a line: Now consider This has the form where So the epipolar lines are

16 .Recovering epipoles 16 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Every epipolar line in image 1 passes through the epipole e 1 . In other words for ALL This can only be true if e 1 is in the nullspace of E . Similarly: We find the null spaces by computing , and taking the last column of and the last row of .

17 .Decomposition of E 17 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Essential matrix: To recover translation and rotation use the matrix: We take the SVD and then we set

18 .Four interpretations 18 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince To get the different solutions, we mutliply t by -1 and substitute

19 .The fundamental matrix 19 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Now consider two cameras that are not normalised By a similar procedure to before, we get the relation or where Relation between essential and fundamental

20 .Fundamental matrix criterion 20 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

21 .When the fundamental matrix is correct, the epipolar line induced by a point in the first image should pass through the matching point in the second image and vice-versa. This suggests the criterion If and then Unfortunately, there is no closed form solution for this quantity. Estimation of fundamental matrix 21 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

22 .The 8 point algorithm 22 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Approach: solve for fundamental matrix using homogeneous coordinates closed form solution (but to wrong problem!) Known as the 8 point algorithm Start with fundamental matrix relation Writing out in full: or

23 .The 8 point algorithm 23 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Can be written as: where Stacking together constraints from at least 8 pairs of points, we get the system of equations

24 .The 8 point algorithm 24 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Minimum direction problem of the form , Find minimum of subject to . To solve, compute the SVD and then set to the last column of .

25 .Fitting concerns 25 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince This procedure does not ensure that solution is rank 2. Solution: set last singular value to zero. Can be unreliable because of numerical problems to do with the data scaling – better to re-scale the data first Needs 8 points in general positions (cannot all be planar). Fails if there is not sufficient translation between the views Use this solution to start non-linear optimisation of true criterion (must ensure non-linear constraints obeyed). There is also a 7 point algorithm (useful if fitting repeatedly in RANSAC)

26 .Structure 26 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Two view geometry The essential and fundamental matrices Reconstruction pipeline Rectification Multi-view reconstruction Applications

27 .Two view reconstruction pipeline 27 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Start with pair of images taken from slightly different viewpoints

28 .Two view reconstruction pipeline 28 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Find features using a corner detection algorithm

29 .Two view reconstruction pipeline 29 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Match features using a greedy algorithm