15_Models_For_Transformations

1 .Computer vision: models, learning and inference Chapter 15 Models for transformations Please send errata to s.prince@cs.ucl.ac.uk

2 .Structure 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Transformation models Learning and inference in transformation models Three problems Exterior orientation Calibration Reconstruction Properties of the homography Robust estimation of transformations Applications

3 .Transformation models 3 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Consider viewing a planar scene There is now a 1 to 1 mapping between points on the plane and points in the image We will investigate models for this 1 to 1 mapping Euclidean Similarity Affine transform Homography

4 .Motivation: augmented reality tracking 4 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

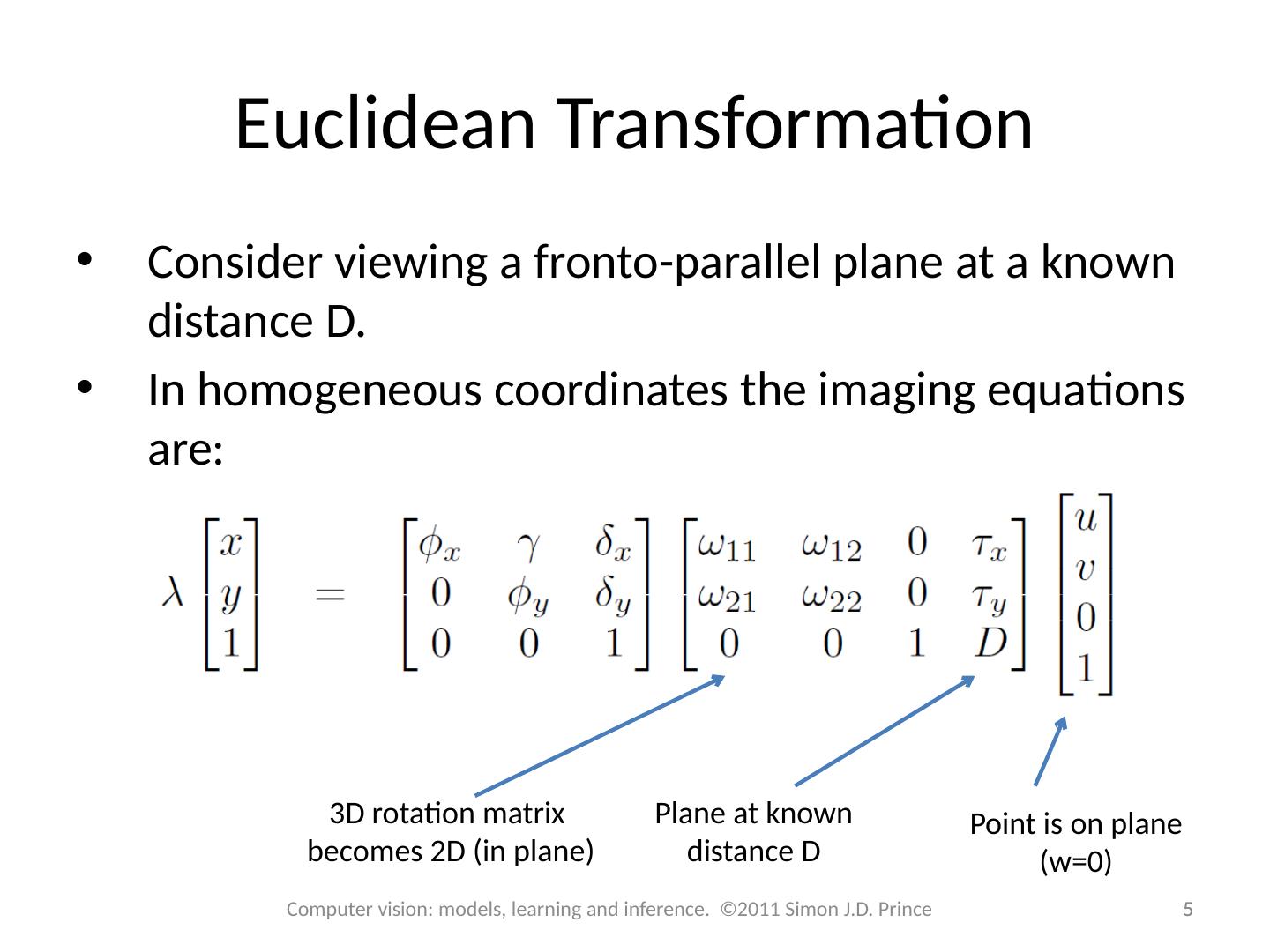
5 .Consider viewing a fronto -parallel plane at a known distance D. In homogeneous coordinates the imaging equations are: Euclidean Transformation 5 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 3D rotation matrix becomes 2D (in plane) Plane at known distance D Point is on plane (w=0)

6 .Euclidean transformation 6 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Simplifying Rearranging the last equation

7 .Euclidean transformation 7 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Simplifying Rearranging the last equation

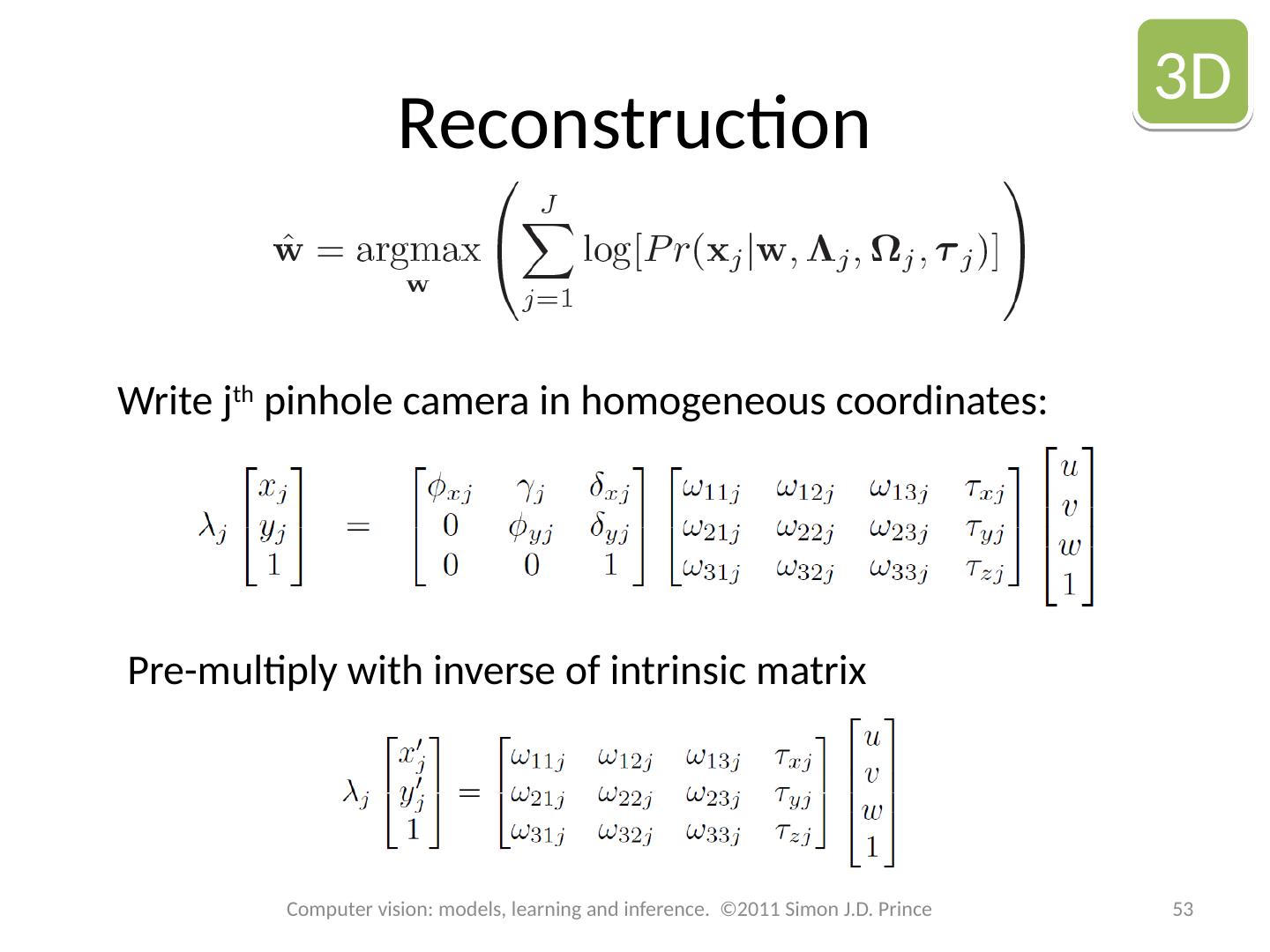
8 .Euclidean transformation 8 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Pre-multiplying by inverse of (modified) intrinsic matrix

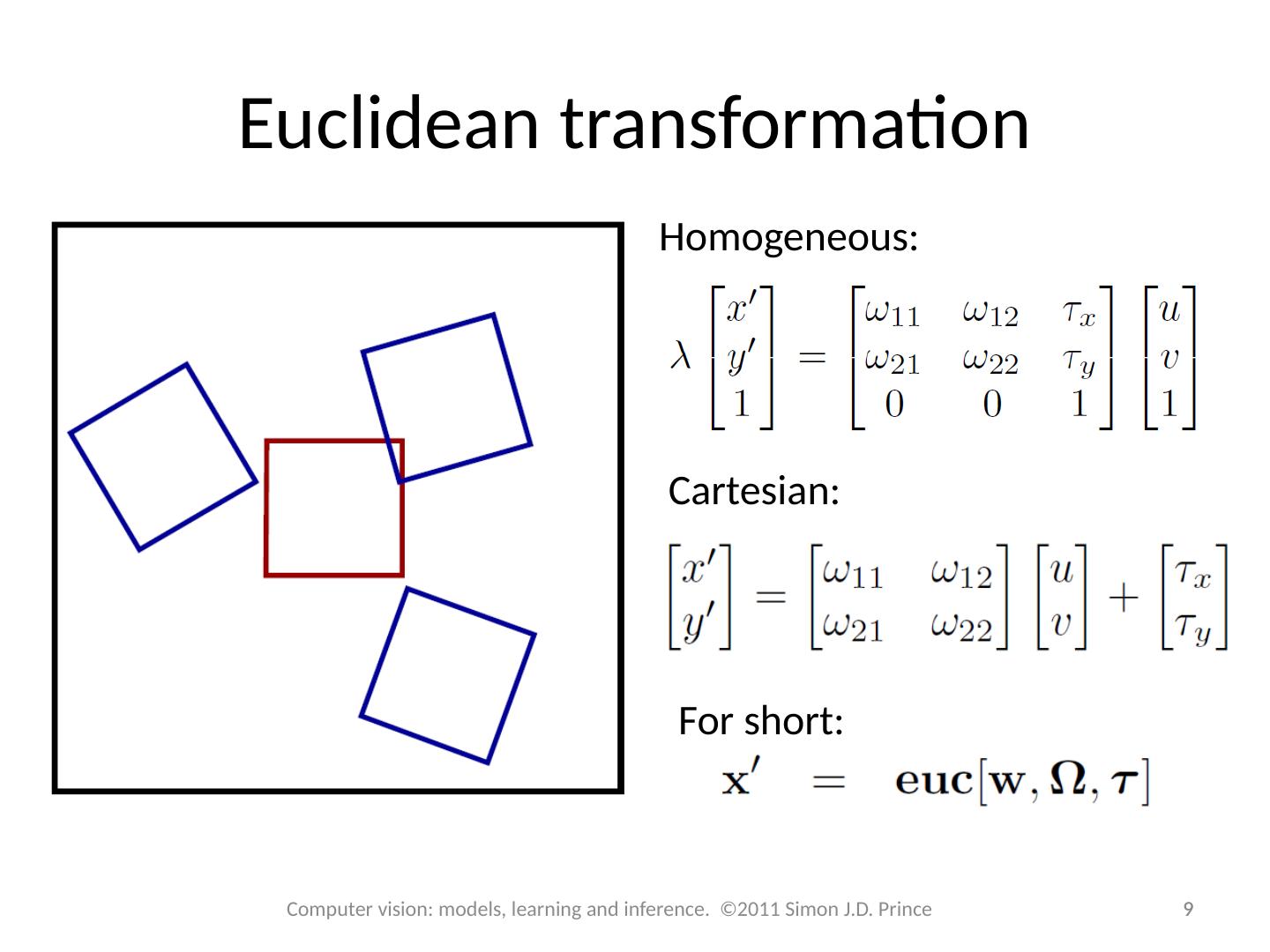
9 .Euclidean transformation 9 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince or for short: Homogeneous: Cartesian: For short:

10 .Similarity Transformation 10 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Consider viewing fronto -parallel plane at unknown distance D By same logic as before we have Premultiplying by inverse of intrinsic matrix

11 .Similarity Transformation 11 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Simplifying: Multiply each equation by :

12 .Similarity Transformation 12 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Simplifying: Incorporate the constants by defining :

13 .Similarity Transformation 13 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Homogeneous: Cartesian: For short:

14 .Affine Transformation 14 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Homogeneous: Cartesian: For short:

15 .Affine Transform 15 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Affine transform describes mapping well when the depth variation within the planar object is small and the camera is far away When variation in depth is comparable to distance to object then the affine transformation is not a good model. Here we need the homography

16 .Projective transformation / collinearity / homography 16 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Start with basic projection equation: Combining these two matrices we get:

17 .Homography 17 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Homogeneous: Cartesian: For short:

18 .Adding noise 18 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince In the real world, the measured image positions are uncertain. We model this with a normal distribution e.g.

19 .Structure 19 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Transformation models Learning and inference in transformation models Three problems Exterior orientation Calibration Reconstruction Properties of the homography Robust estimation of transformations Applications

20 .Learning and inference problems 20 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Learning – take points on plane and their projections into the image and learn transformation parameters Inference – take the projection of a point in the image and establish point on plane

21 .Learning and inference problems 21 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

22 .Learning transformation models 22 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Maximum likelihood approach Becomes a least squares problem

23 .Learning Euclidean parameters 23 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Solve for transformation: Remaining problem:

24 .This is an orthogonal Procrustes problem. To solve: Compute SVD And then set Learning Euclidean parameters 24 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Has the general form:

25 .Learning similarity parameters 25 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Solve for rotation matrix as before Solve for translation and scaling factor

26 .Learning affine parameters 26 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Affine transform is linear Solve using least-squares solution

27 .Learning homography parameters 27 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Homography is not linear – cannot be solved in closed form. Convert to other homogeneous coordinates Both sides are 3x1 vectors; should be parallel and so cross product will be zero

28 .Write out these equations in full There are only 2 independent equations here – use a minimum of four points to build up a set of equations Learning homography parameters 28 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

29 .These equations have the form , which we need to solve with the constraint This is a minimum direction problem Compute SVD Take last column of Then use non-linear optimization Learning homography parameters 29 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince