14_The_Pinhole_Camera

1 .Computer vision: models, learning and inference Chapter 14 The pinhole camera

2 .Structure Pinhole camera model Three geometric problems Homogeneous coordinates Solving the problems Exterior orientation problem Camera calibration 3D reconstruction Applications 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

3 .Motivation 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Sparse stereo reconstruction Compute the depth at a set of sparse matching points

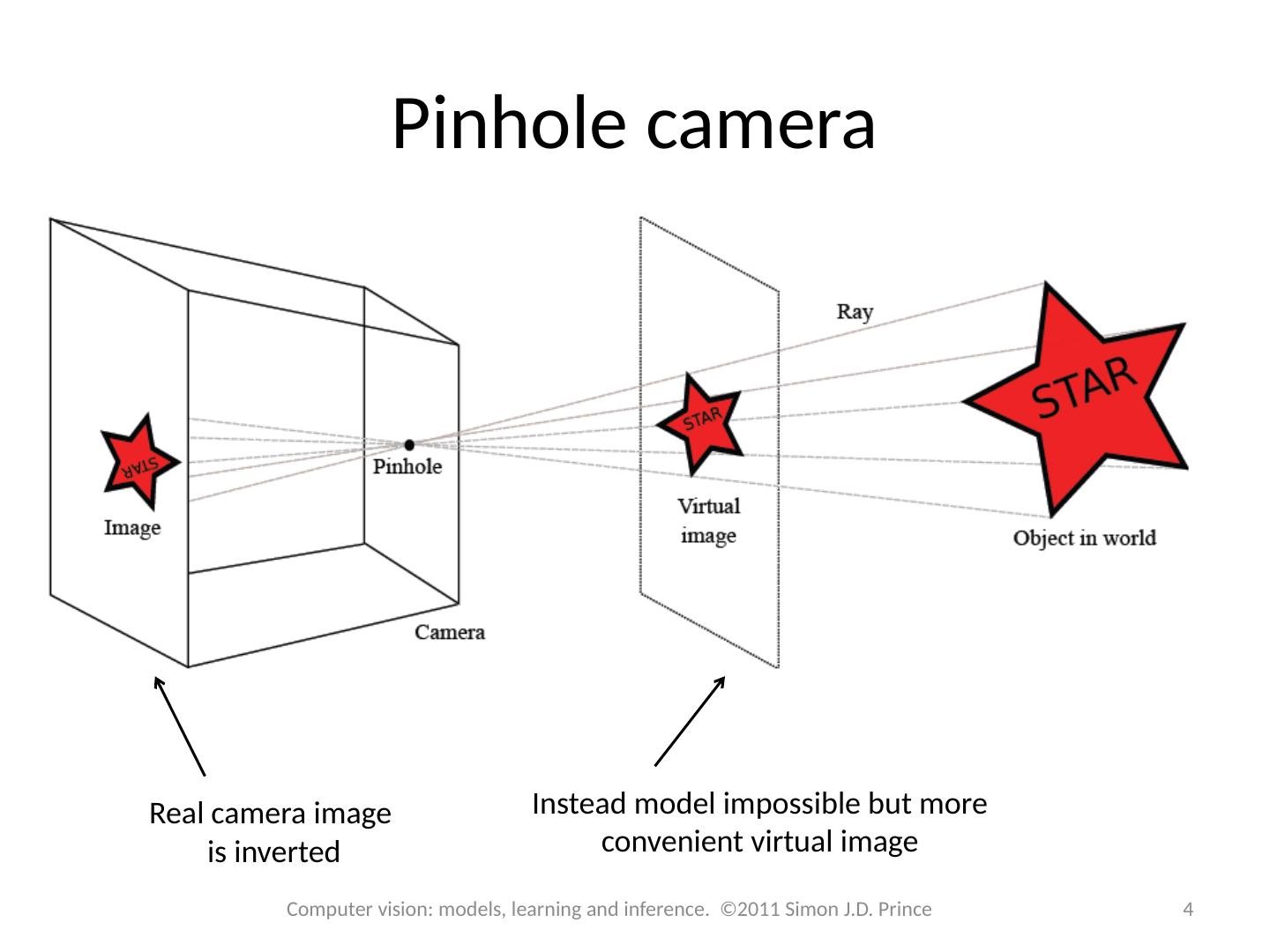
4 .Pinhole camera 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Real camera image is inverted Instead model impossible but more convenient virtual image

5 .Pinhole camera terminology 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

6 .Normalized Camera 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince By similar triangles:

7 .Focal length parameters 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

8 .Can model both the effect of the distance to the focal plane the density of the receptors with a single focal length parameter f In practice, the receptors may not be square: So use different focal length parameter for x and y dims Focal length parameters 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

9 .Offset parameters 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Current model assumes that pixel (0,0) is where the principal ray strikes the image plane (i.e. the center) Model offset to center

10 .Finally, add skew parameter Accounts for image plane being not exactly perpendicular to the principal ray Skew parameter 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

11 .Position w =( u,v,w ) T of point in the world is generally not expressed in the frame of reference of the camera. Transform using 3D transformation or Position and orientation of camera 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Point in frame of reference of camera Point in frame of reference of world

12 .Intrinsic parameters (stored as intrinsic matrix) Extrinsic parameters Complete pinhole camera model 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

13 .For short: Add noise – uncertainty in localizing feature in image Complete pinhole camera model 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

14 .Radial distortion 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

15 .Structure Pinhole camera model Three geometric problems Homogeneous coordinates Solving the problems Exterior orientation problem Camera calibration 3D reconstruction Applications 15 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

16 .Problem 1: Learning extrinsic parameters (exterior orientation) 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Use maximum likelihood:

17 .Problem 2 – Learning intrinsic parameters (calibration) 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Use maximum likelihood:

18 .Calibration 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Use 3D target with known 3D points

19 .Problem 3 – Inferring 3D points (triangulation / reconstruction) 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Use maximum likelihood: TO Change

20 .Solving the problems 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince None of these problems can be solved in closed form Can apply non-linear optimization to find best solution but slow and prone to local minima Solution – convert to a new representation (homogeneous coordinates) where we can solve in closed form. Caution! We are not solving the true problem – finding global minimum of wrong* problem. But can use as starting point for non-linear optimization of true problem *= We’ll first minimize algebraic error, instead of geometric error (see Minimizing Algebraic Error in Geometric Estimation Problems, Hartley 1998 )

21 .Structure Pinhole camera model Three geometric problems Homogeneous coordinates Solving the problems Exterior orientation problem Camera calibration 3D reconstruction Applications 21 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

22 .Homogeneous coordinates 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Convert 2D coordinate to 3D To convert back

23 .Geometric interpretation of homogeneous coordinates 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

24 .Pinhole camera in homogeneous coordinates 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Camera model: In homogeneous coordinates: (linear!)

25 .Pinhole camera in homogeneous coordinates 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Writing out these three equations Eliminate l to retrieve original equations

26 .Adding in extrinsic parameters 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Or for short: Or even shorter:

27 .Structure Pinhole camera model Three geometric problems Homogeneous coordinates Solving the problems Exterior orientation problem Camera calibration 3D reconstruction Applications 27 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

28 .Problem 1: Learning extrinsic parameters (exterior orientation) 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Use maximum likelihood:

29 .Exterior orientation 29 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Start with camera equation in homogeneous coordinates Pre-multiply both sides by inverse of camera calibration matrix