- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
11_Models_For_Chains_And_Trees
展开查看详情
1 .Computer vision: models, learning and inference Chapter 11 Models for Chains and Trees
2 .Structure Chain and tree models MAP inference in chain models MAP inference in tree models Maximum marginals in chain models Maximum marginals in tree models Models with loops Applications 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
3 .Chain and tree models Given a set of measurements and world states , infer the world states from the measurements. Problem: if N is large, then the model relating the two will have a very large number of parameters. Solution: build sparse models where we only describe subsets of the relations between variables. 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
4 .Chain and tree models 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Chain model: only model connections between a world variable and its 1 predeeding and 1 subsequent variables Tree model: connections between world variables are organized as a tree (no loops). Disregard directionality of connections for directed model
5 .Assumptions 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince We’ll assume that World states are discrete Observed data variables for each world state The n th data variable is conditionally independent of all of other data variables and world states, given associated world state
6 .See also: Thad Starner’s work Gesture Tracking 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
7 .Directed model for chains (Hidden Markov model) 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Compatibility of measurement and world state Compatibility of world state and previous world state
8 .Undirected model for chains 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Compatibility of measurement and world state Compatibility of world state and previous world state
9 .Equivalence of chain models 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Directed: Undirected: Equivalence:
10 .Chain model for sign language application 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Observations are normally distributed but depend on sign k World state is categorically distributed, parameters depend on previous world state
11 .Structure Chain and tree models MAP inference in chain models MAP inference in tree models Maximum marginals in chain models Maximum marginals in tree models Models with loops Applications 11 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
12 .MAP inference in chain model 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince MAP inference: Substituting in : Directed model:
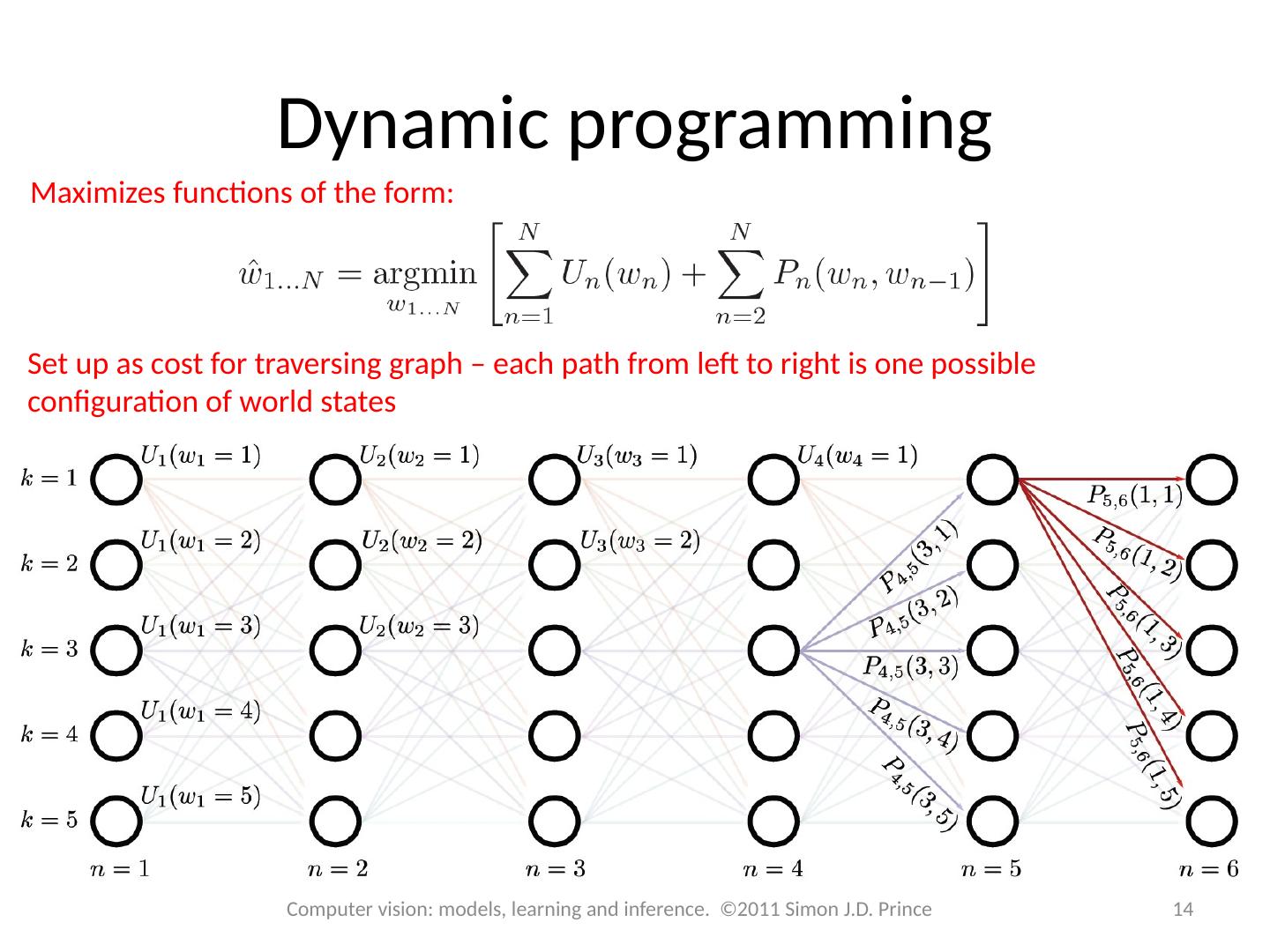
13 .MAP inference in chain model 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Takes the general form: Unary term: Pairwise term:
14 .Dynamic programming 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Maximizes functions of the form: Set up as cost for traversing graph – each path from left to right is one possible configuration of world states
15 .Dynamic programming 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Algorithm: Work through graph computing minimum possible cost to reach each node When we get to last column, find minimum Trace back to see how we got there
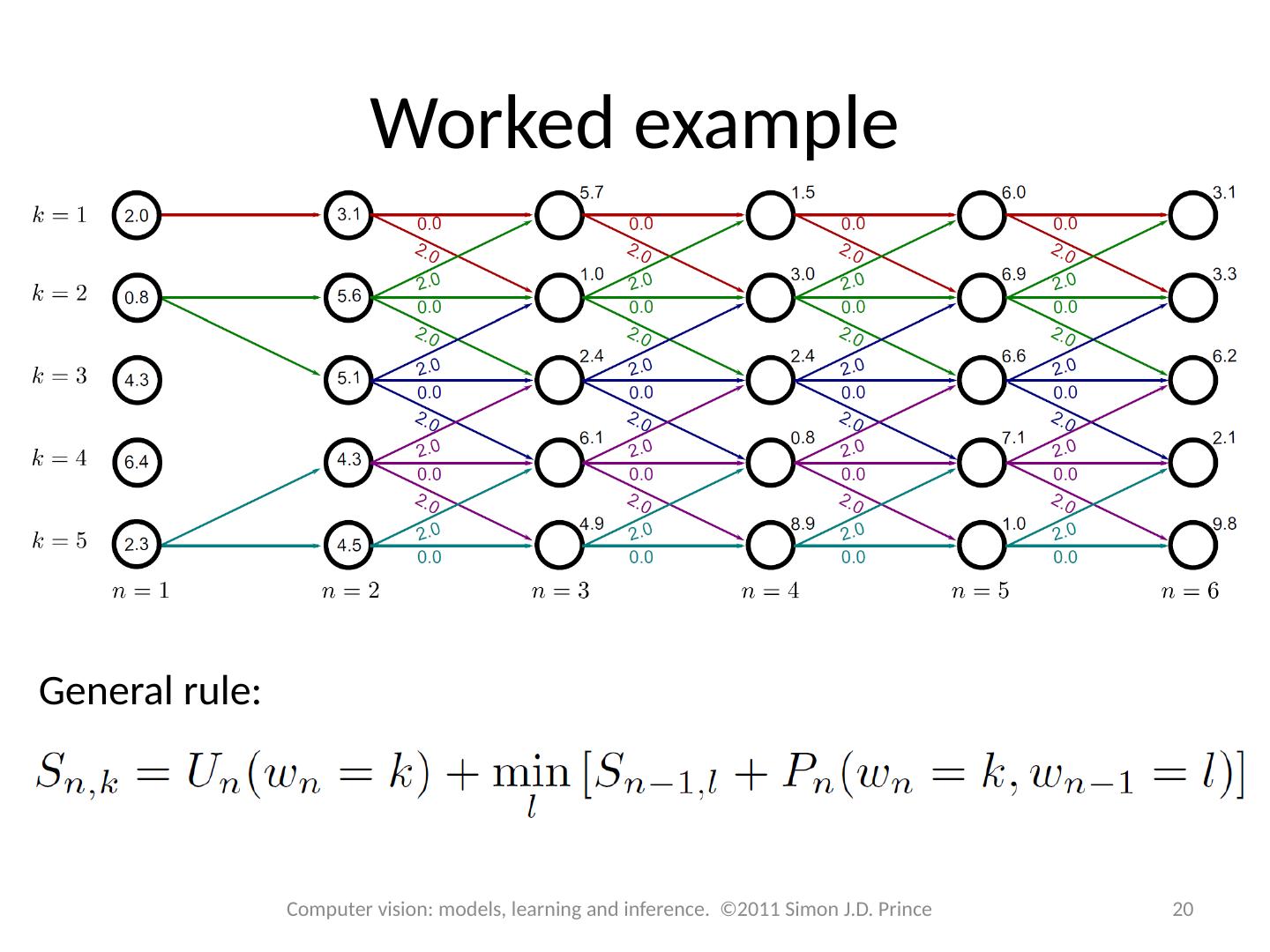
16 .Worked example 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Unary cost Pairwise costs: Zero cost to stay at same label Cost of 2 to change label by 1 Infinite cost for changing by more than one (not shown)
17 .Worked example 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Minimum cost to reach first node is just unary cost
18 .Worked example 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Minimum cost is minimum of two possible routes to get here Route 1: 2.0+0.0+1.1 = 3.1 Route 2: 0.8+2.0+1.1 = 3.9
19 .Worked example 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Minimum cost is minimum of two possible routes to get here Route 1: 2.0+0.0+1.1 = 3.1 -- this is the minimum – note this down Route 2: 0.8+2.0+1.1 = 3.9
20 .Worked example 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince General rule:
21 .Worked example 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Work through the graph, computing the minimum cost to reach each node
22 .Worked example 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Keep going until we reach the end of the graph
23 .Worked example 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Find the minimum possible cost to reach the final column
24 .Worked example 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Trace back the route that we arrived here by – this is the minimum configuration
25 .Structure Chain and tree models MAP inference in chain models MAP inference in tree models Maximum marginals in chain models Maximum marginals in tree models Models with loops Applications 25 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
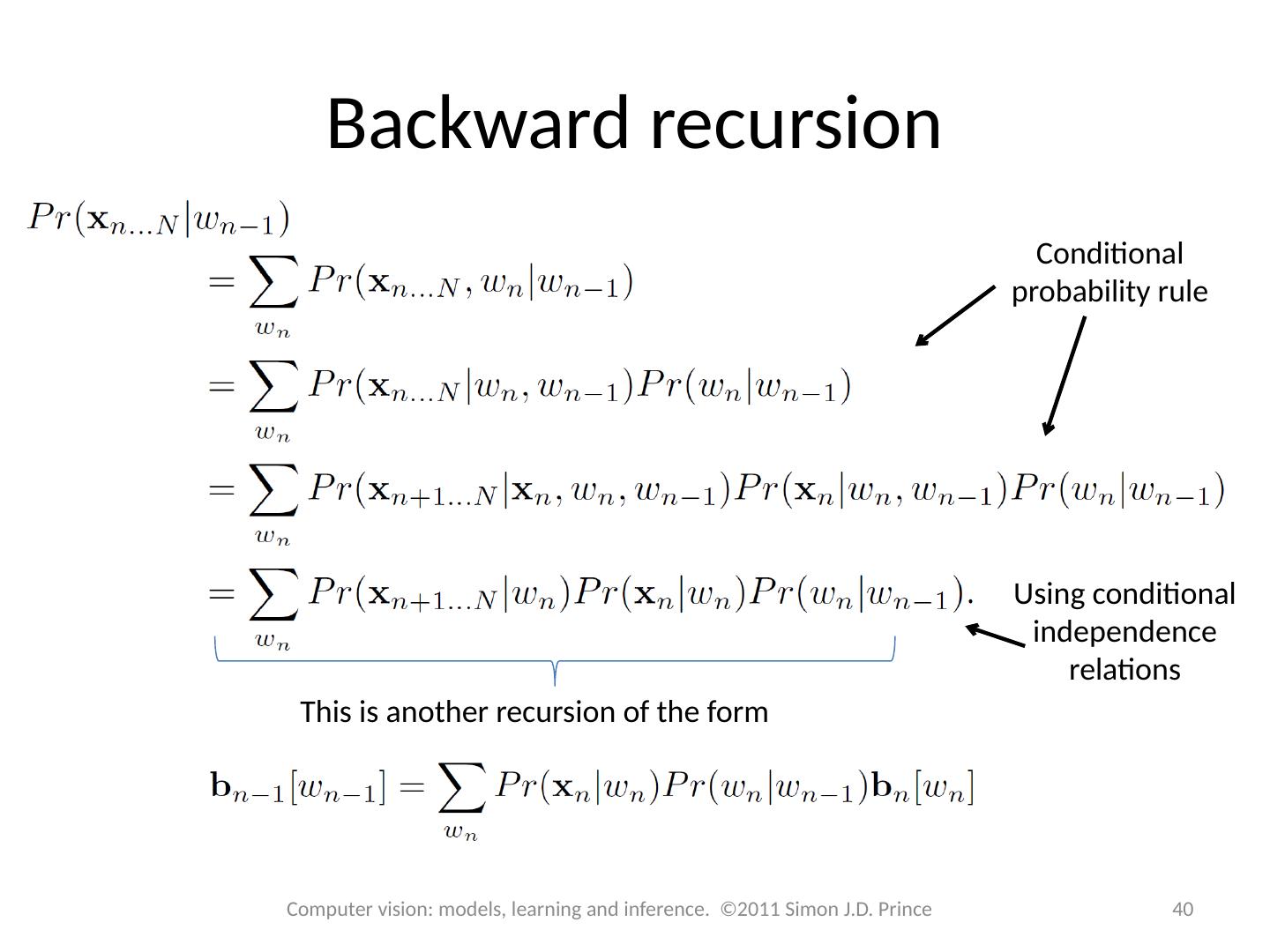
26 .MAP inference for trees 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
27 .MAP inference for trees 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
28 .Worked example 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
29 .Worked example 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Variables 1-4 proceed as for the chain example.