- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
10_Graphical_Models
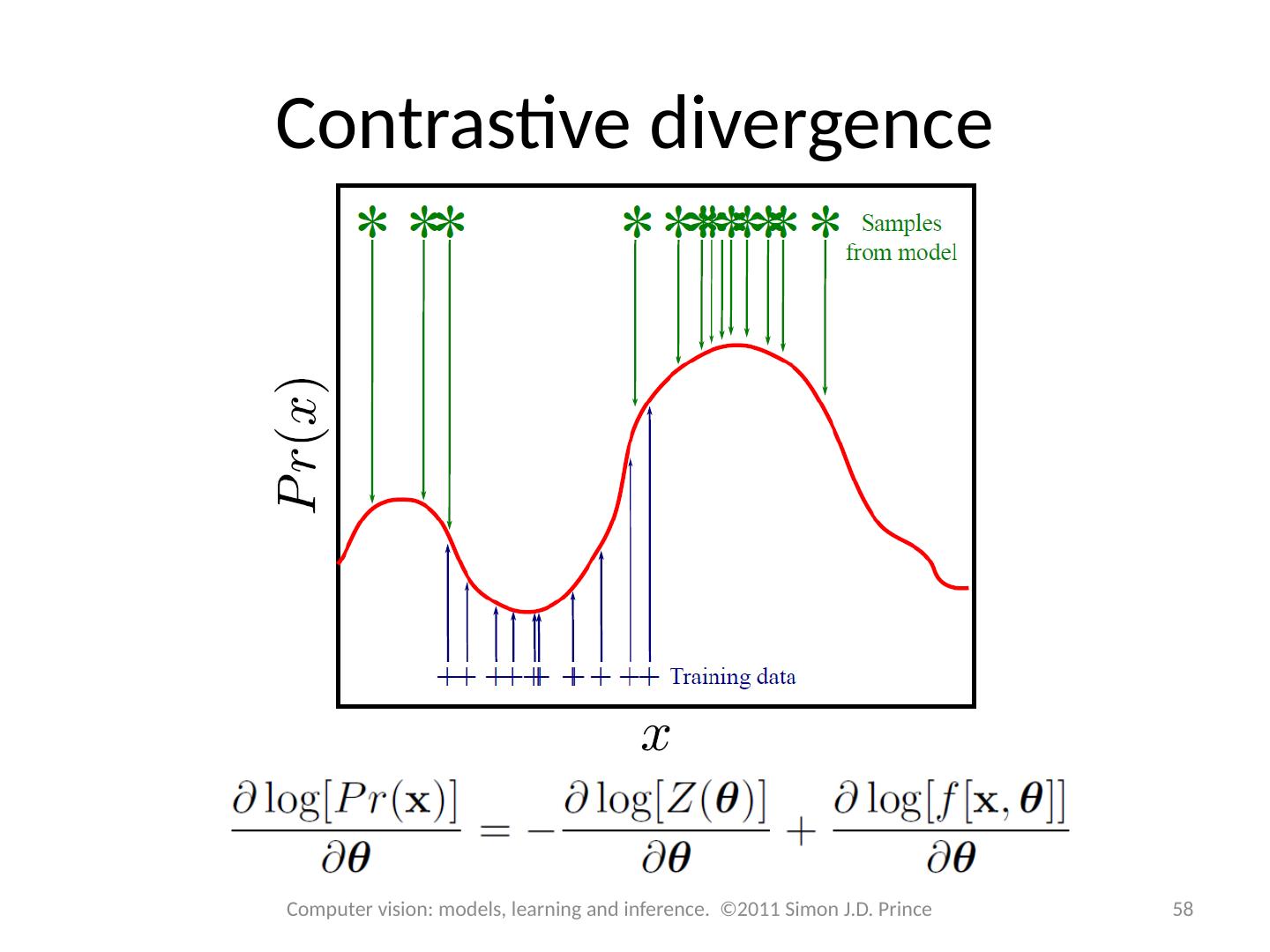
展开查看详情
1 .Computer vision: models, learning and inference Chapter 10 Graphical Models
2 .Independence 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Two variables x 1 and x 2 are independent if their joint probability distribution factorizes as Pr(x 1 , x 2 )= Pr(x 1 ) Pr(x 2 )
3 .Conditional independence 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince The variable x 1 is said to be conditionally independent of x 3 given x 2 when x 1 and x 3 are independent for fixed x 2 . When this is true the joint density factorizes in a certain way and is hence redundant.
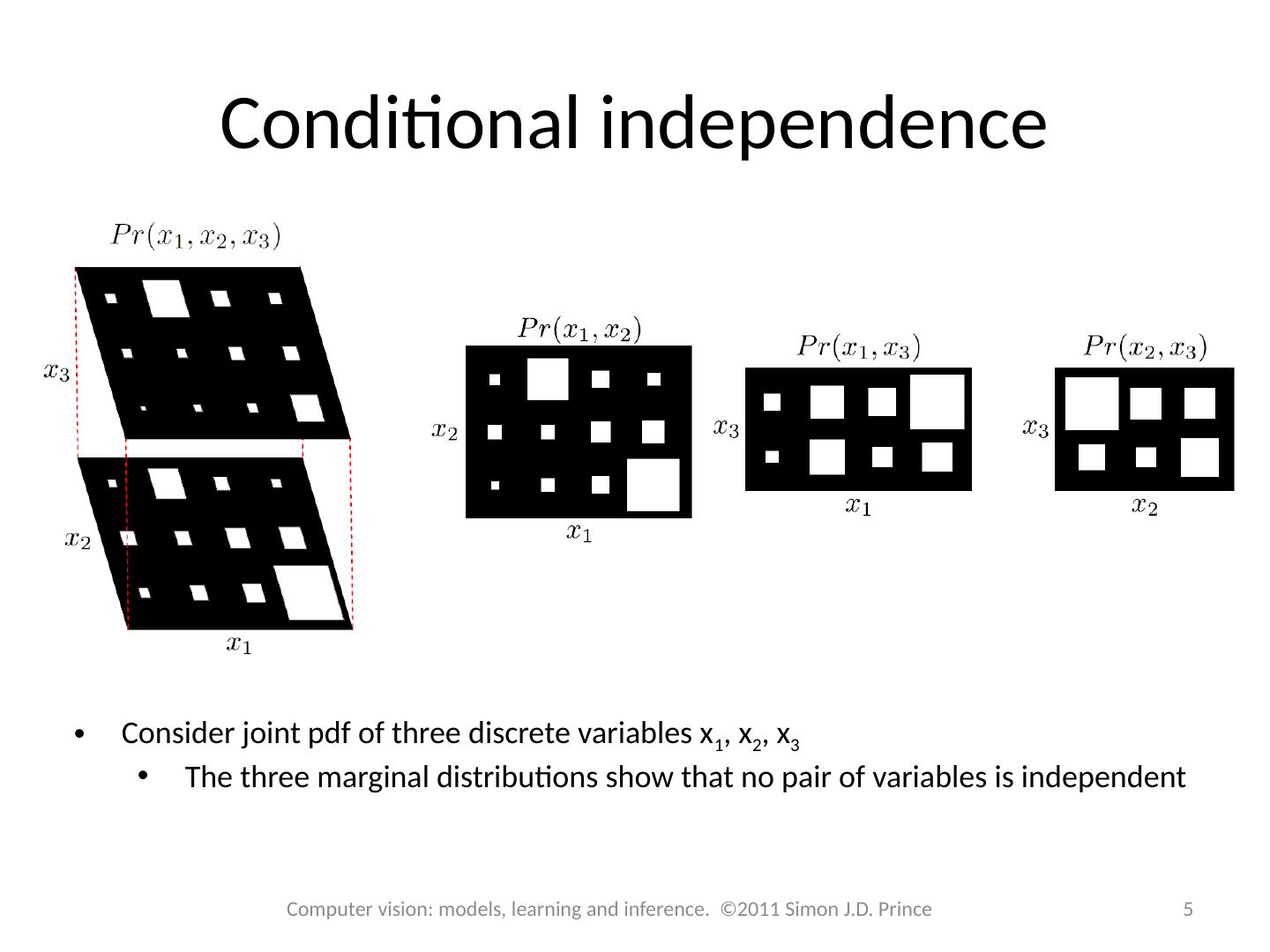
4 .Conditional independence 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Consider joint pdf of three discrete variables x 1 , x 2 , x 3
5 .Conditional independence 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Consider joint pdf of three discrete variables x 1 , x 2 , x 3 The three marginal distributions show that no pair of variables is independent
6 .Conditional independence 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Consider joint pdf of three discrete variables x 1 , x 2 , x 3 The three marginal distributions show that no pair of variables is independent But x 1 is independent of x 2 given x 3
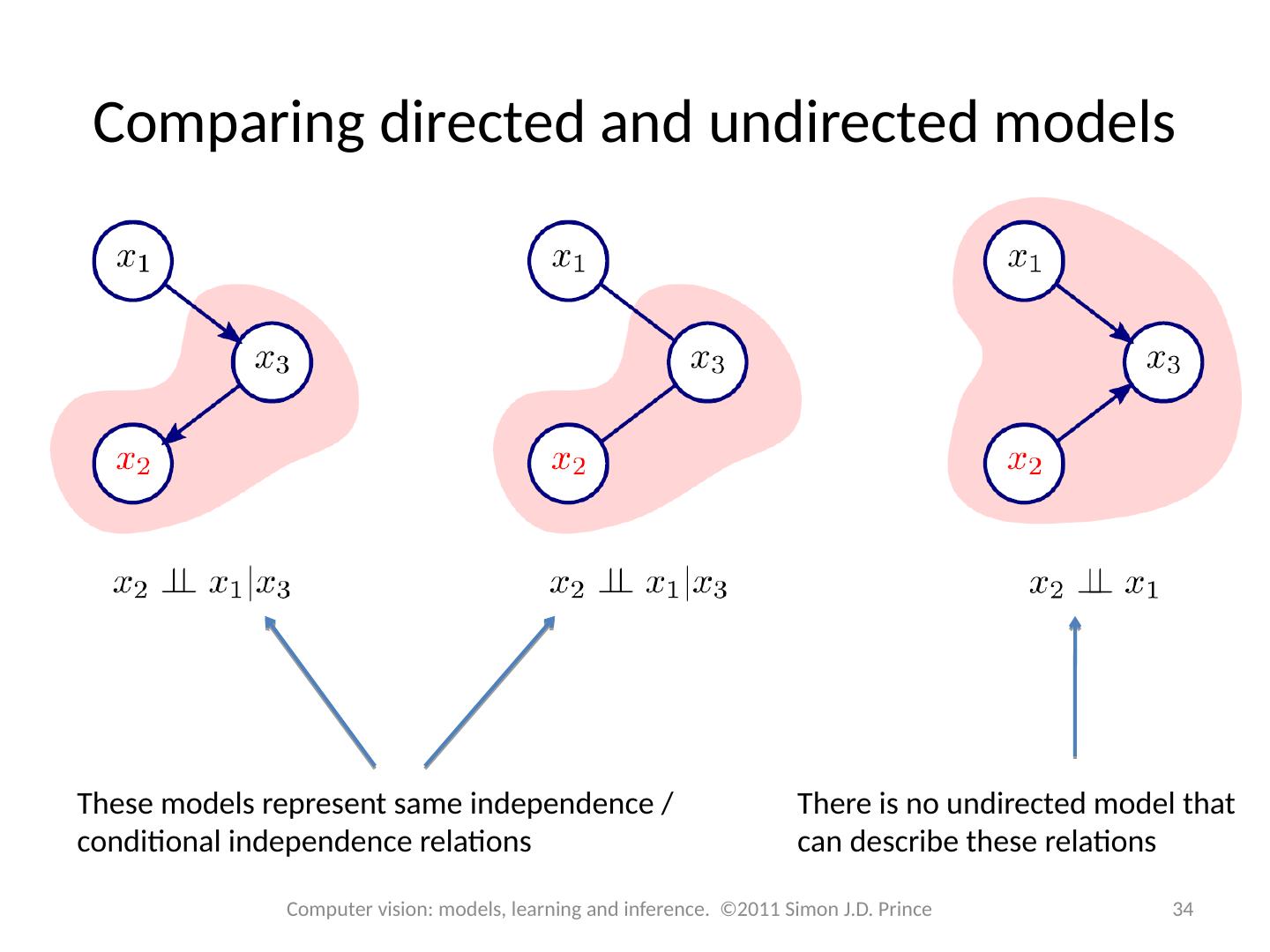
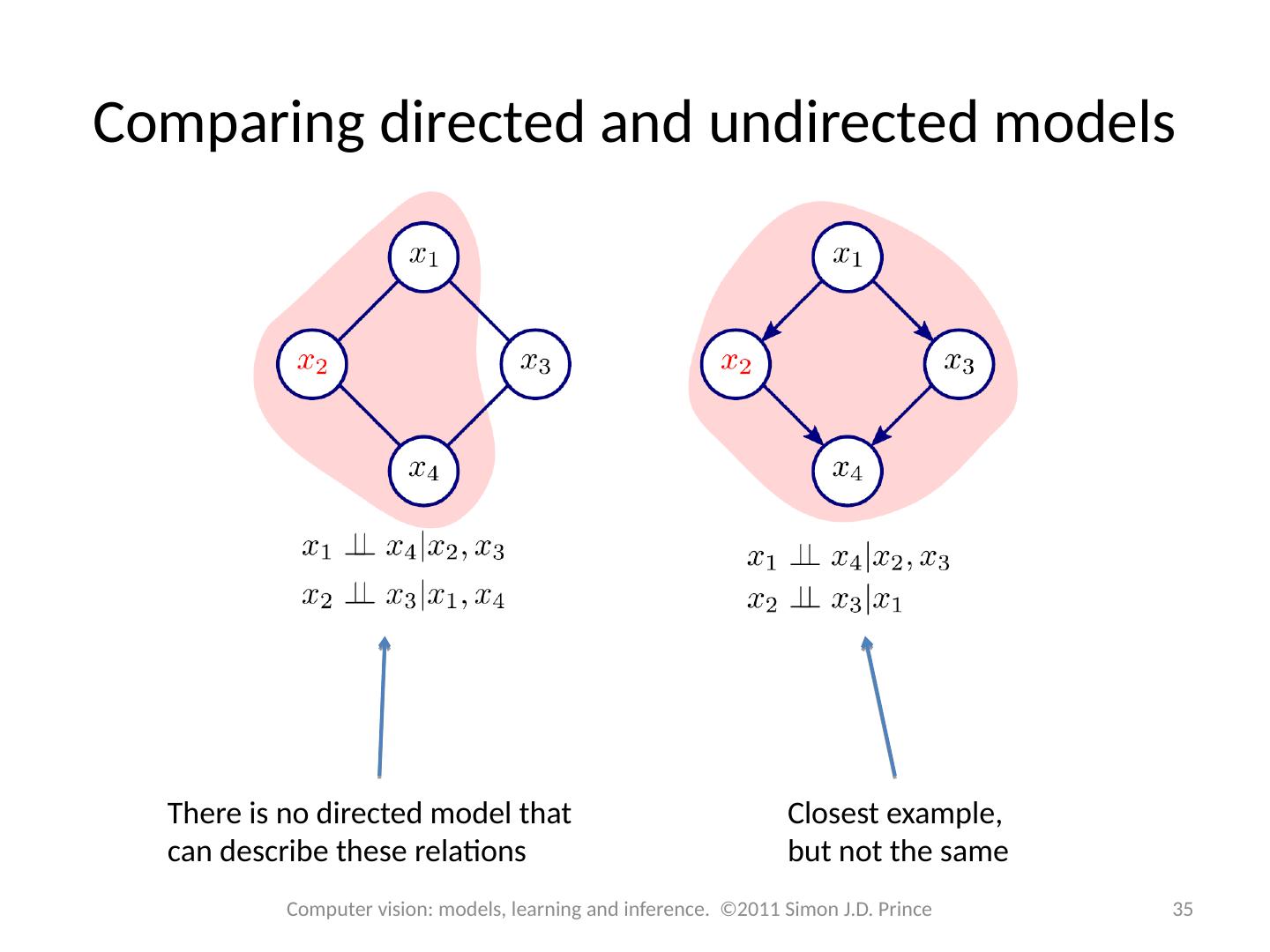
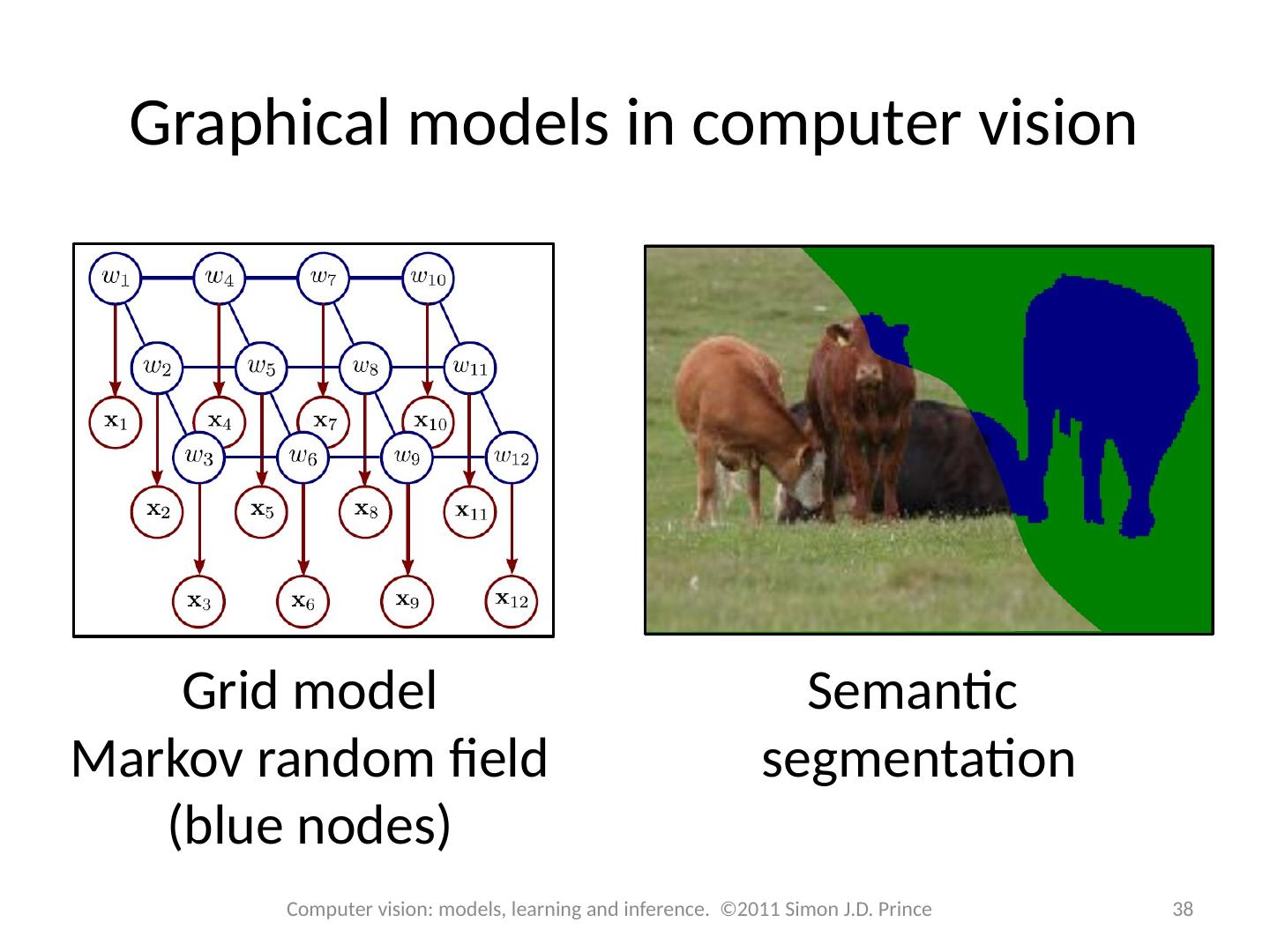
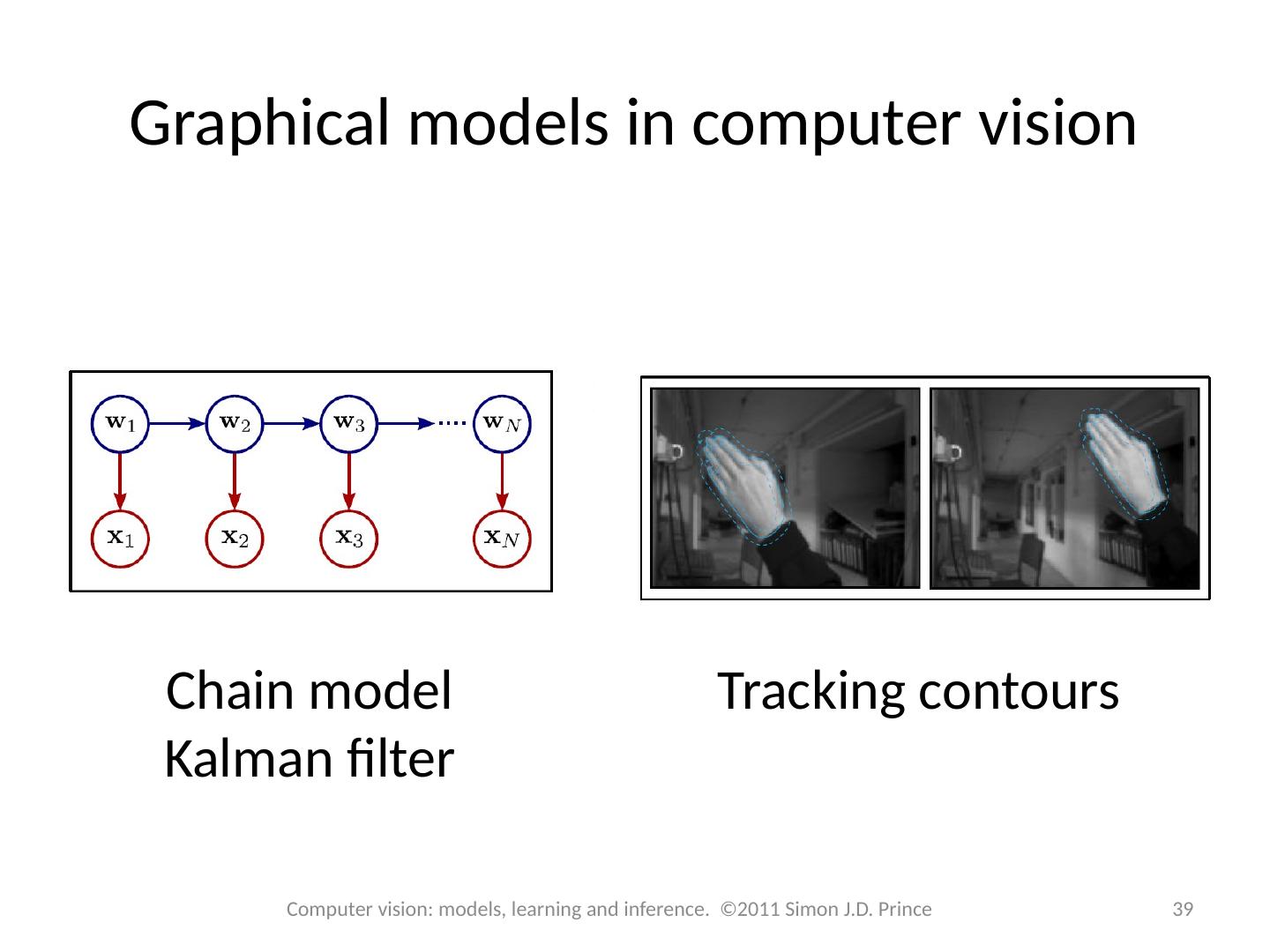
7 .Graphical models A graphical model is a graph based representation that makes both factorization and conditional independence relations easy to establish Two important types: Directed graphical model or Bayesian network Undirected graphical model or Markov network 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
8 .Directed graphical models Directed graphical model represents probability distribution that factorizes as a product of conditional probability distributions where pa[n] denotes the parents of node n 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
9 .Directed graphical models 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince To visualize graphical model from factorization add one node per random variable and draw arrow to each variable from each of its parents. To extract factorization from graphical model Add one term per node in the graph Pr( x n | x pa [n] ) If no parents then just add Pr( x n )
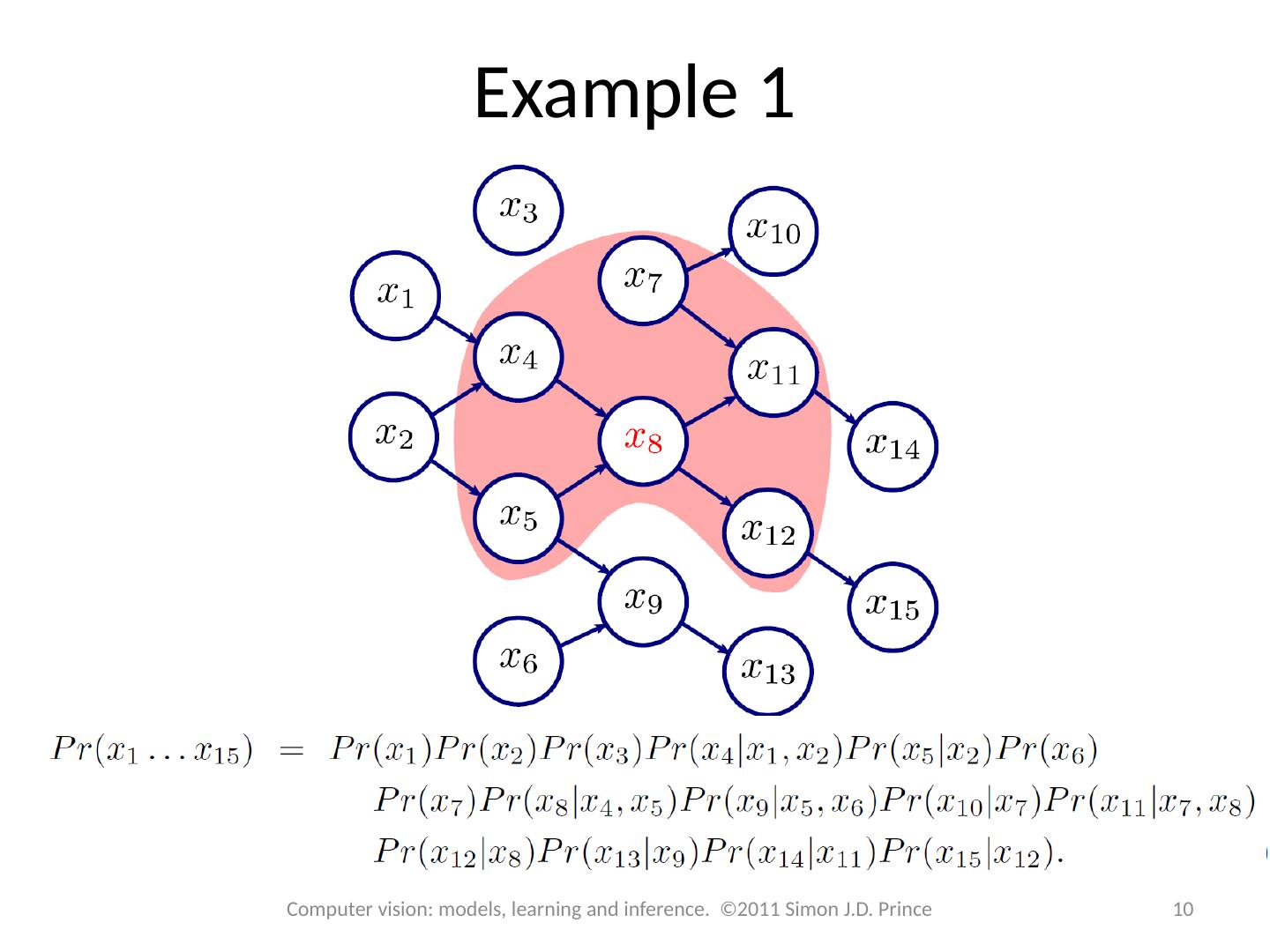
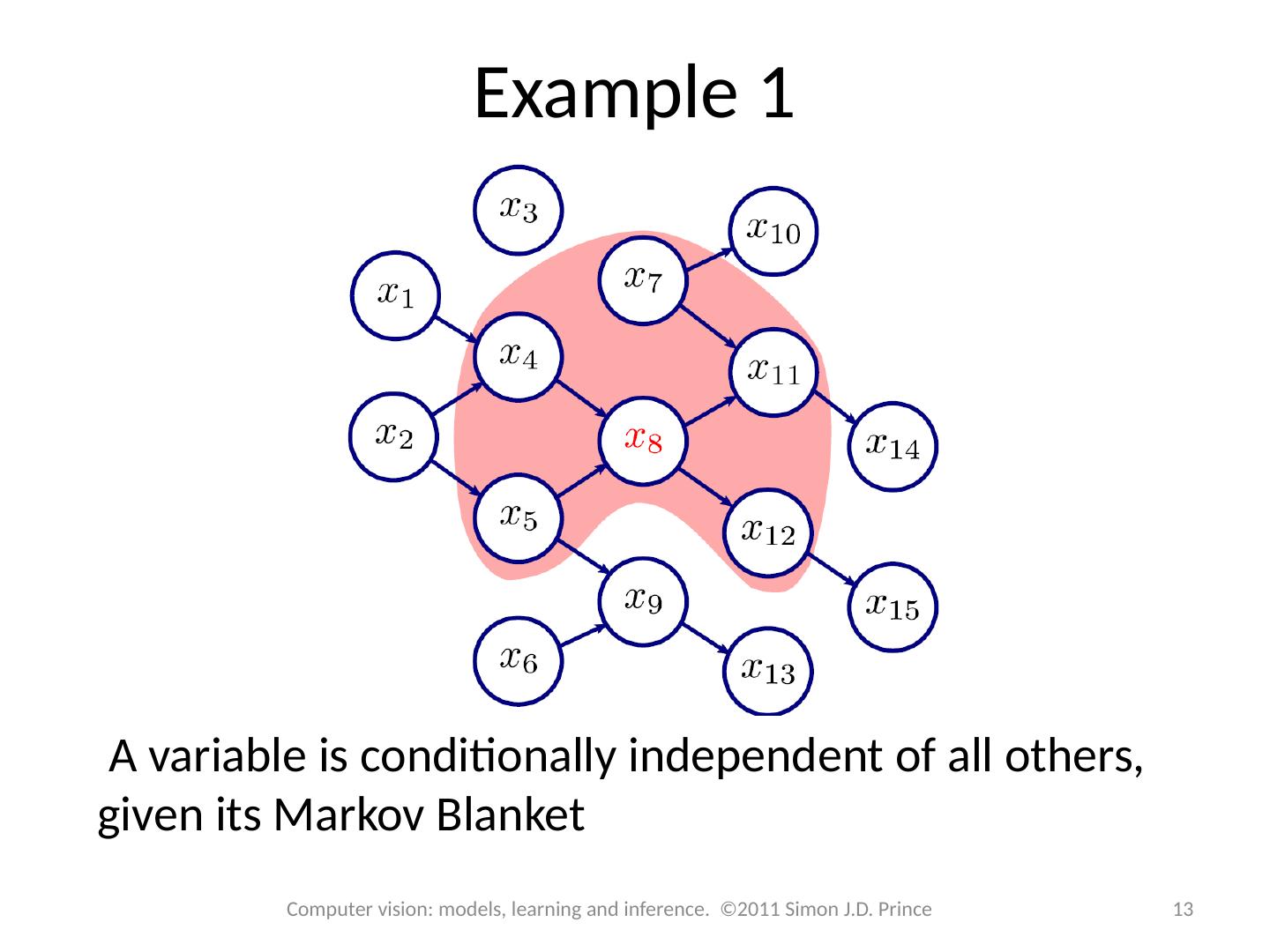
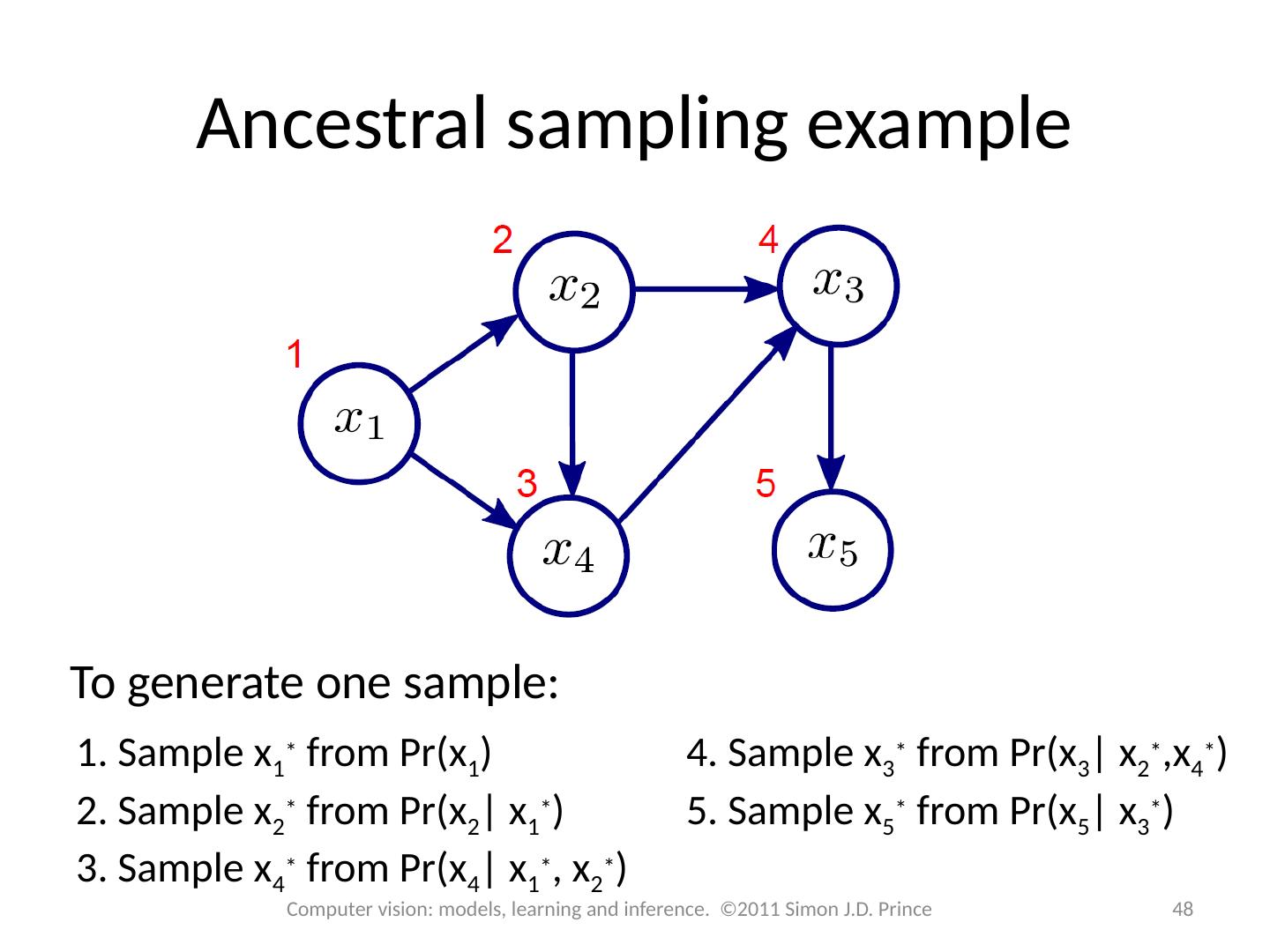
10 .Example 1 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince
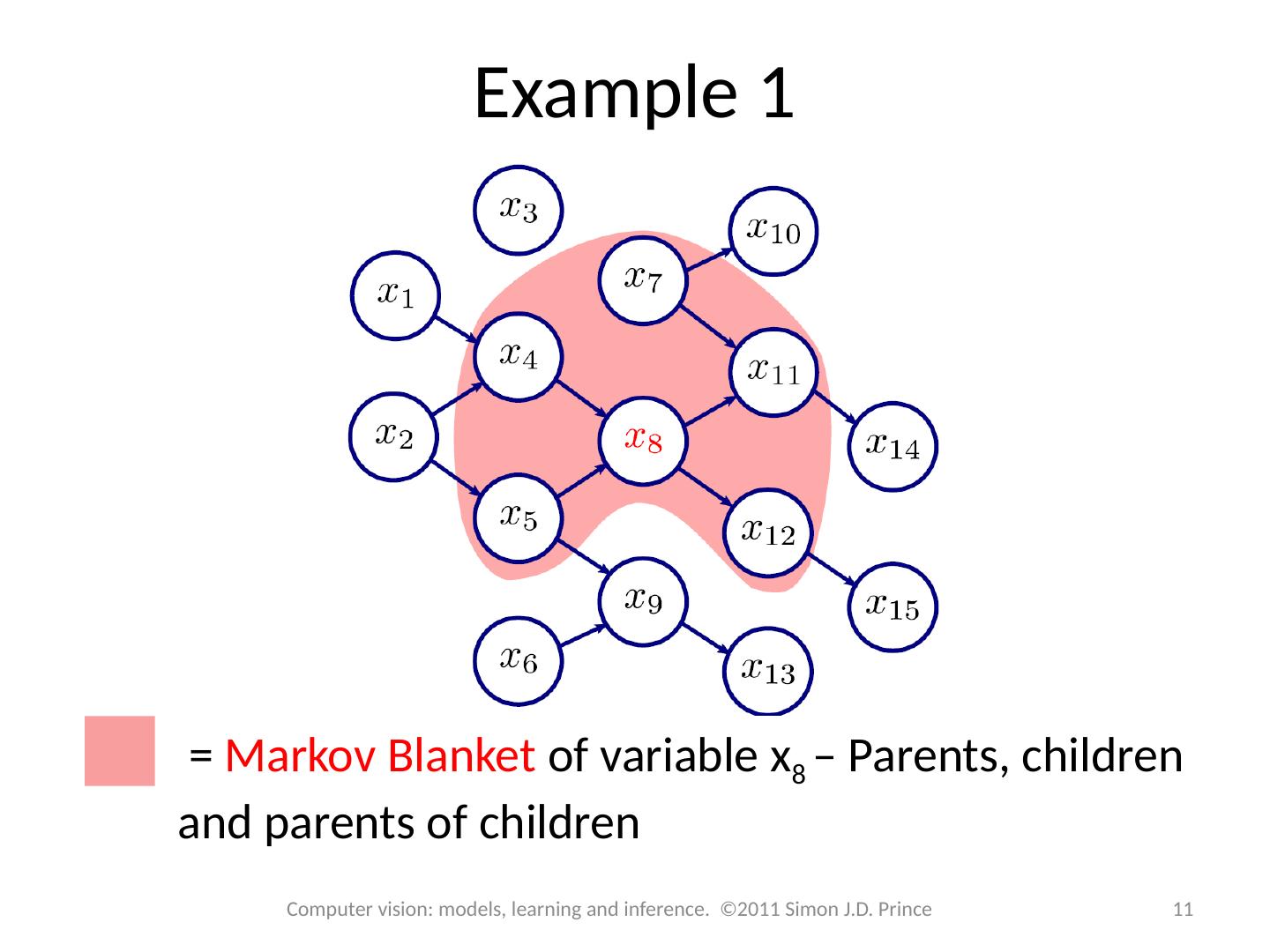
11 .Example 1 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince = Markov Blanket of variable x 8 – Parents, children and parents of children
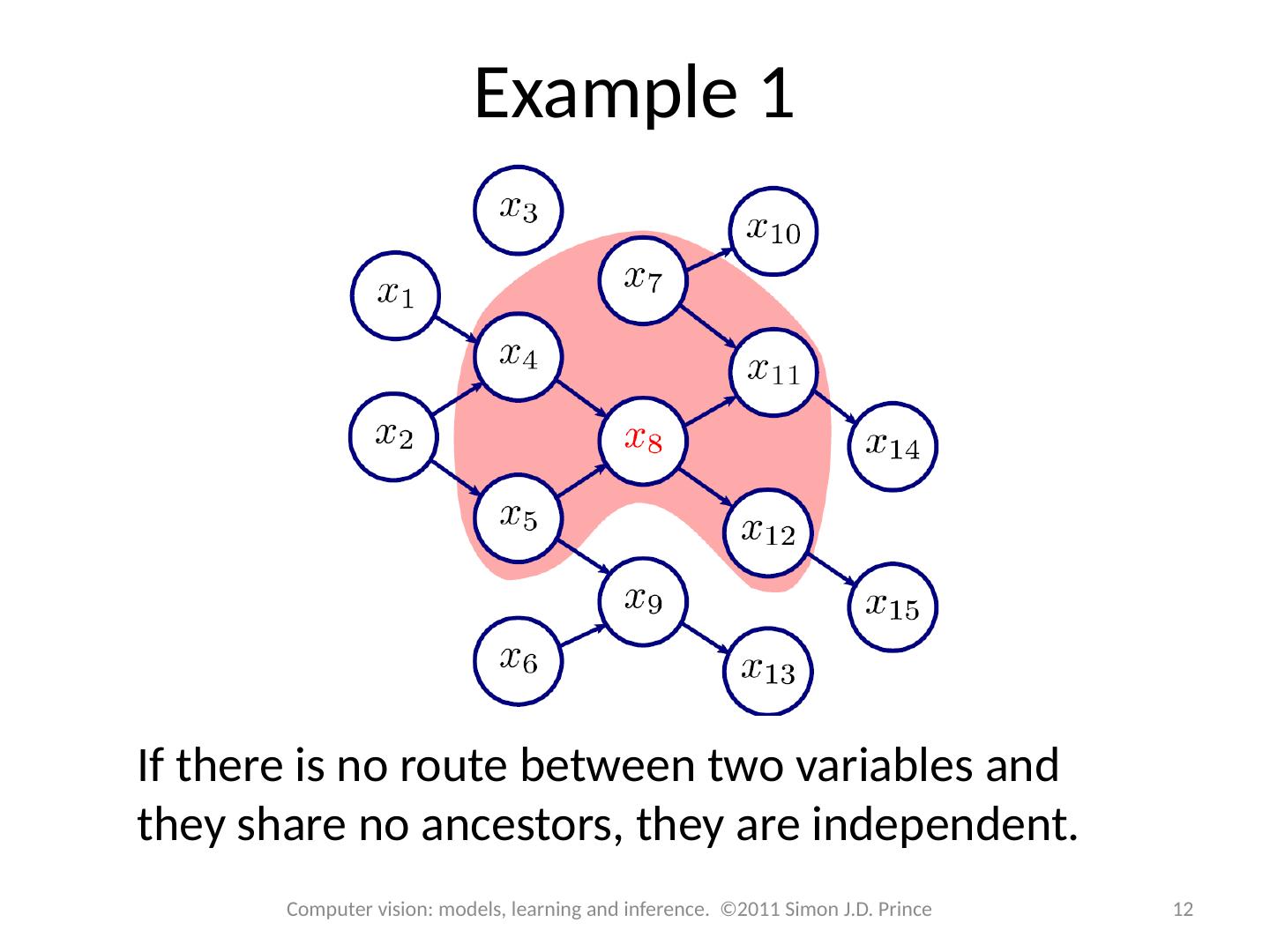
12 .Example 1 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince If there is no route between two variables and they share no ancestors, they are independent.
13 .Example 1 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince A variable is conditionally independent of all others, given its Markov Blanket
14 .Example 1 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince General rule:
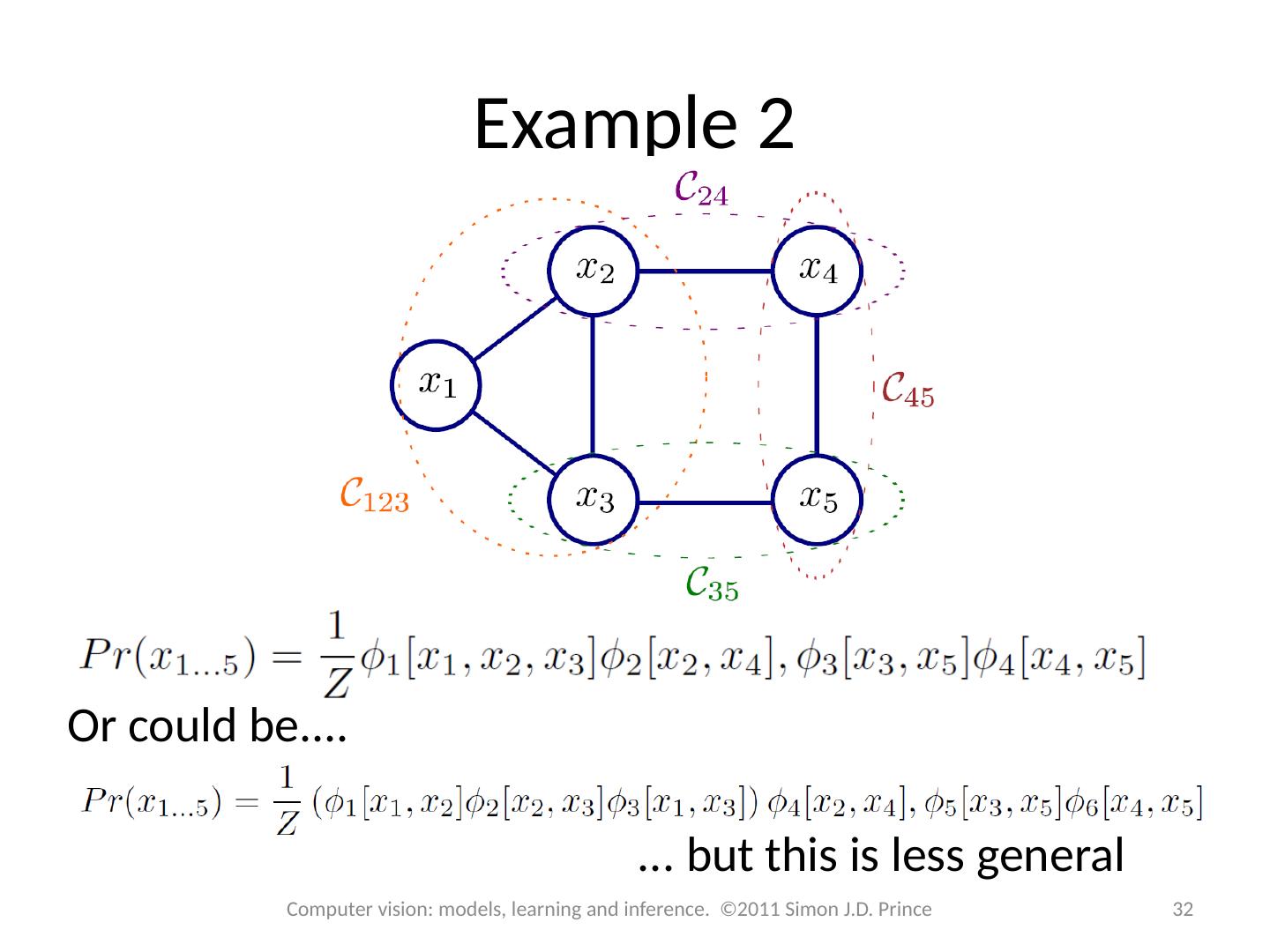
15 .Example 2 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince The joint pdf of this graphical model factorizes as:
16 .Example 2 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince The joint pdf of this graphical model factorizes as: It describes the original example:
17 .Example 2 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince General rule: Here the arrows meet head to tail at x 2 , and so x 1 is conditionally independent of x 3 given x 2 .
18 .Example 2 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Algebraic proof: No dependence on x 3 implies that x 1 is conditionally independent of x 3 given x 2 .
19 .Redundancy 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 4 x 3 x 2 = 24 entries + 3 x 4 + 2 x 3 = 22 entries Conditional independence can be thought of as redundancy in the full distribution Redundancy here only very small, but with larger models can be very significant.
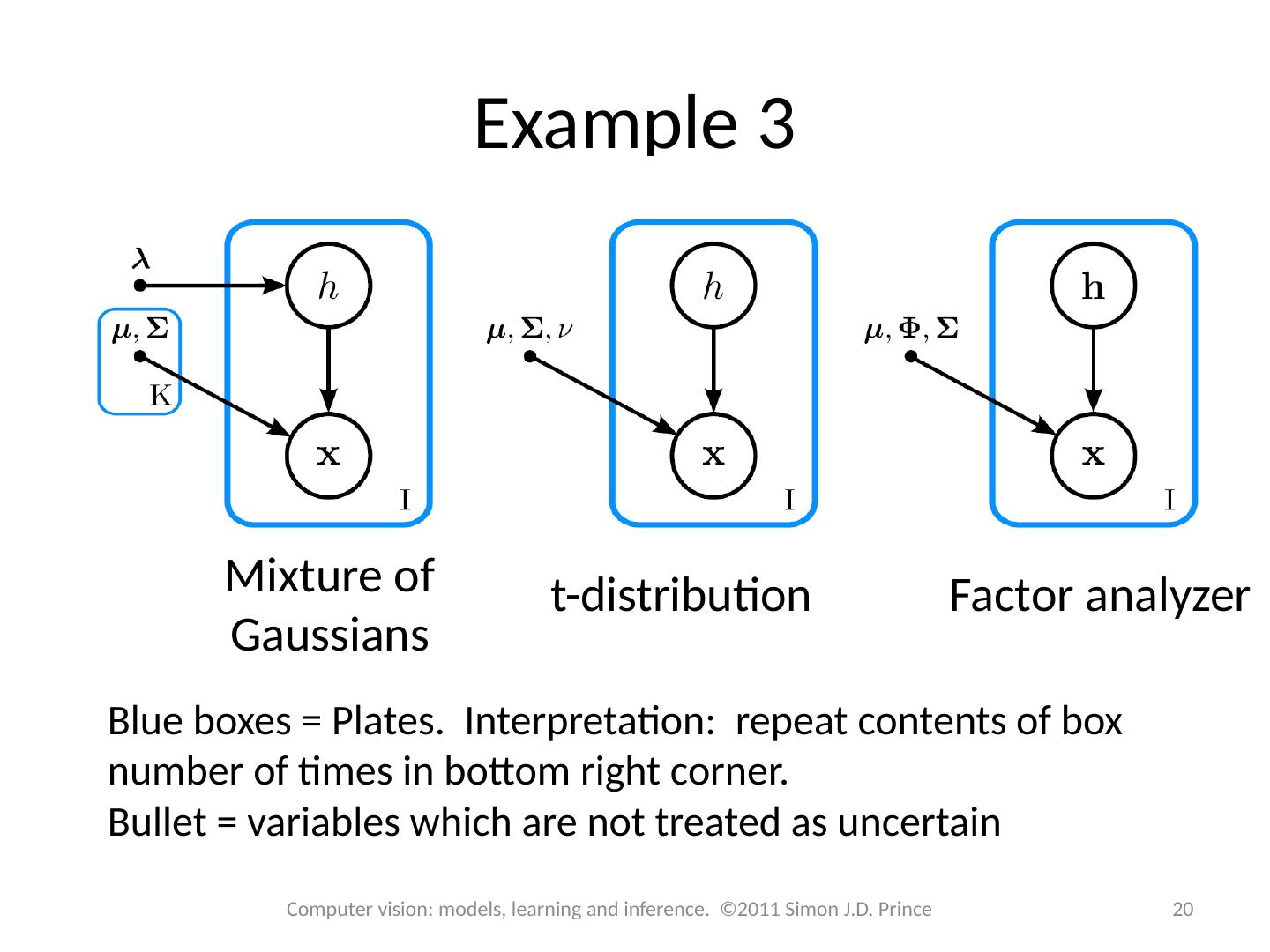
20 .Example 3 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Mixture of Gaussians t-distribution Factor analyzer Blue boxes = Plates. Interpretation: repeat contents of box number of times in bottom right corner. Bullet = variables which are not treated as uncertain
21 .Undirected graphical models 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Probability distribution factorizes as: Partition function (normalization constant) Product over C functions Potential function (returns non-negative number)
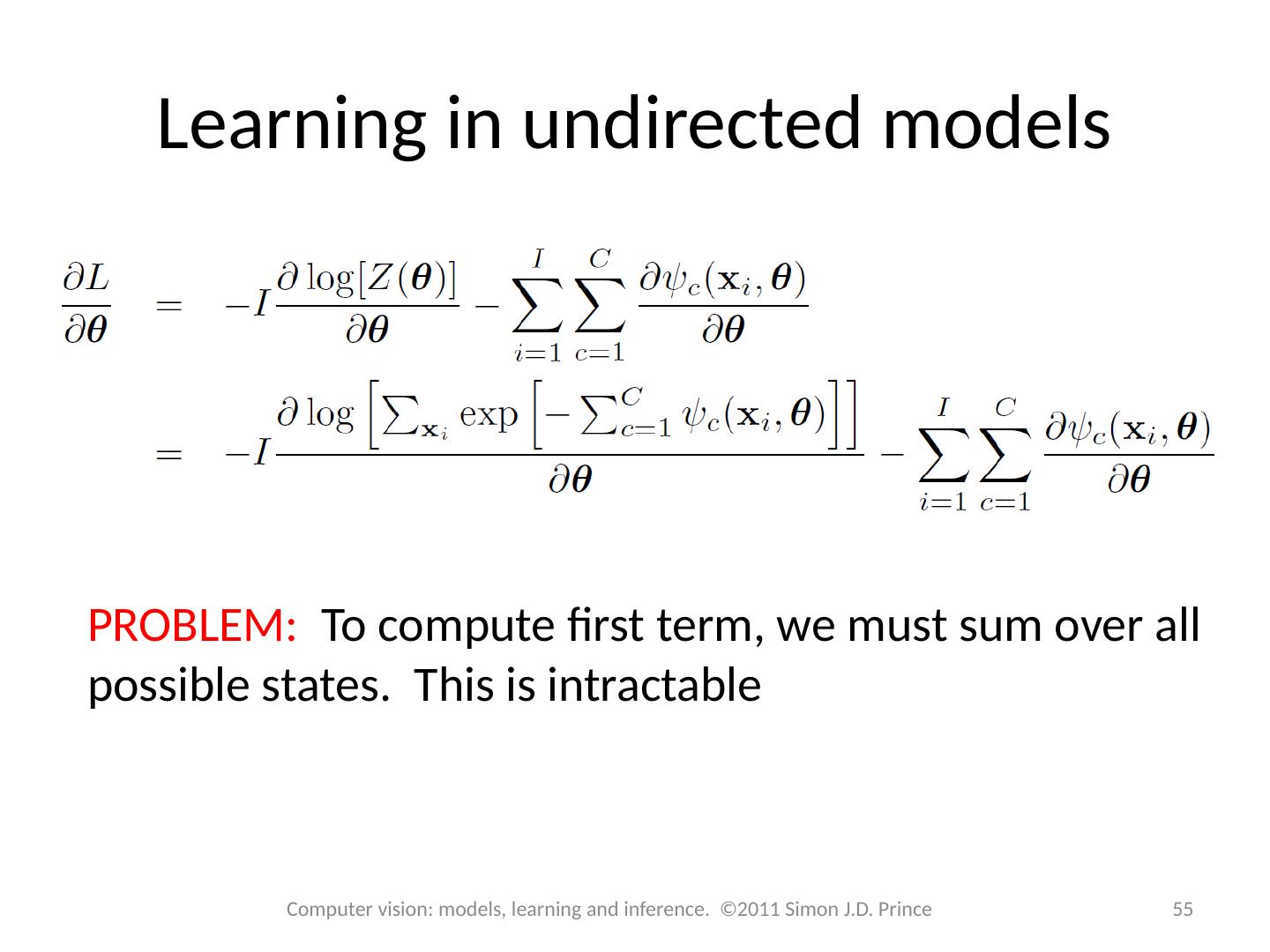
22 .Undirected graphical models 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Probability distribution factorizes as: Partition function (normalization constant) For large systems, intractable to compute
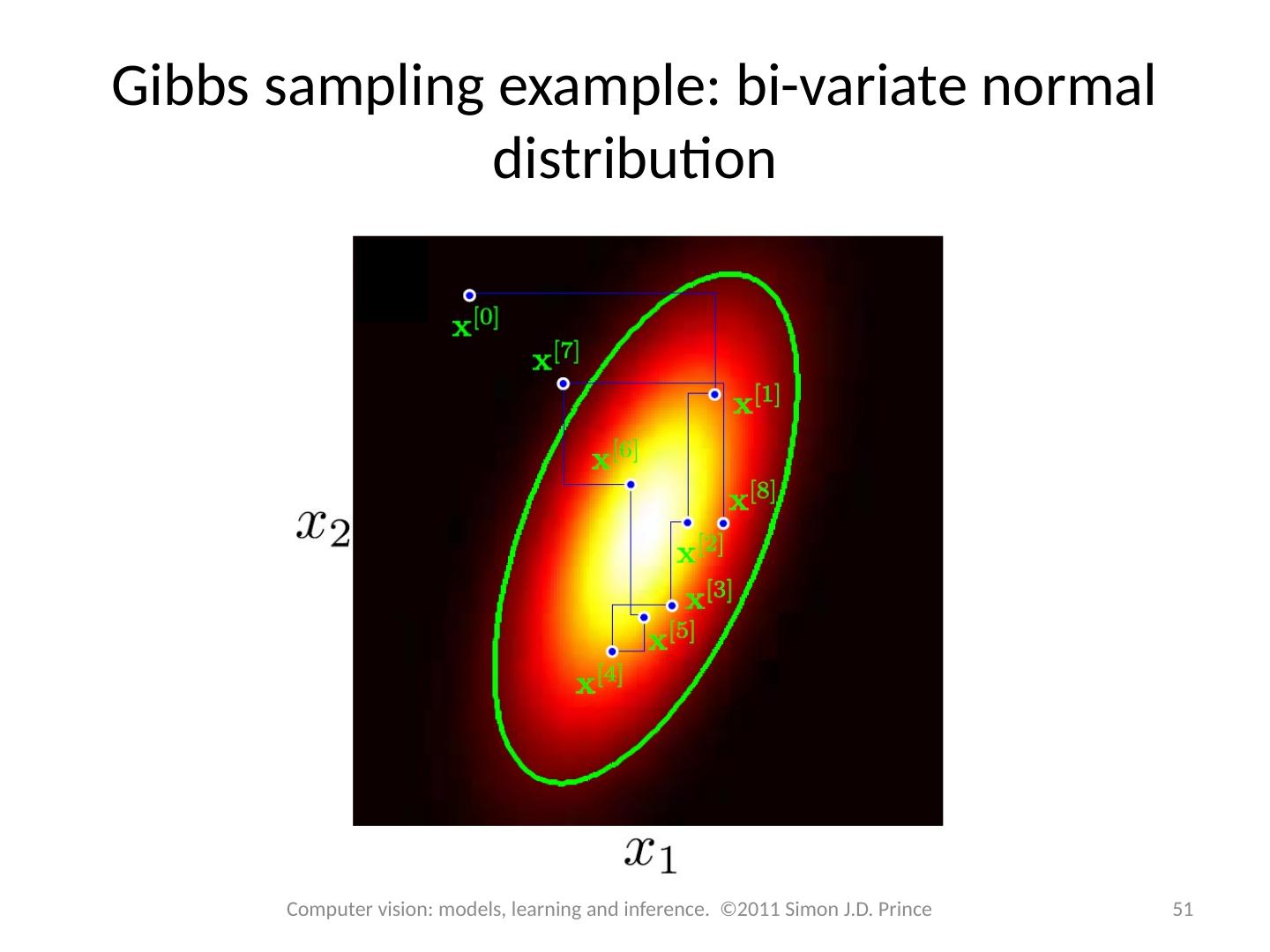
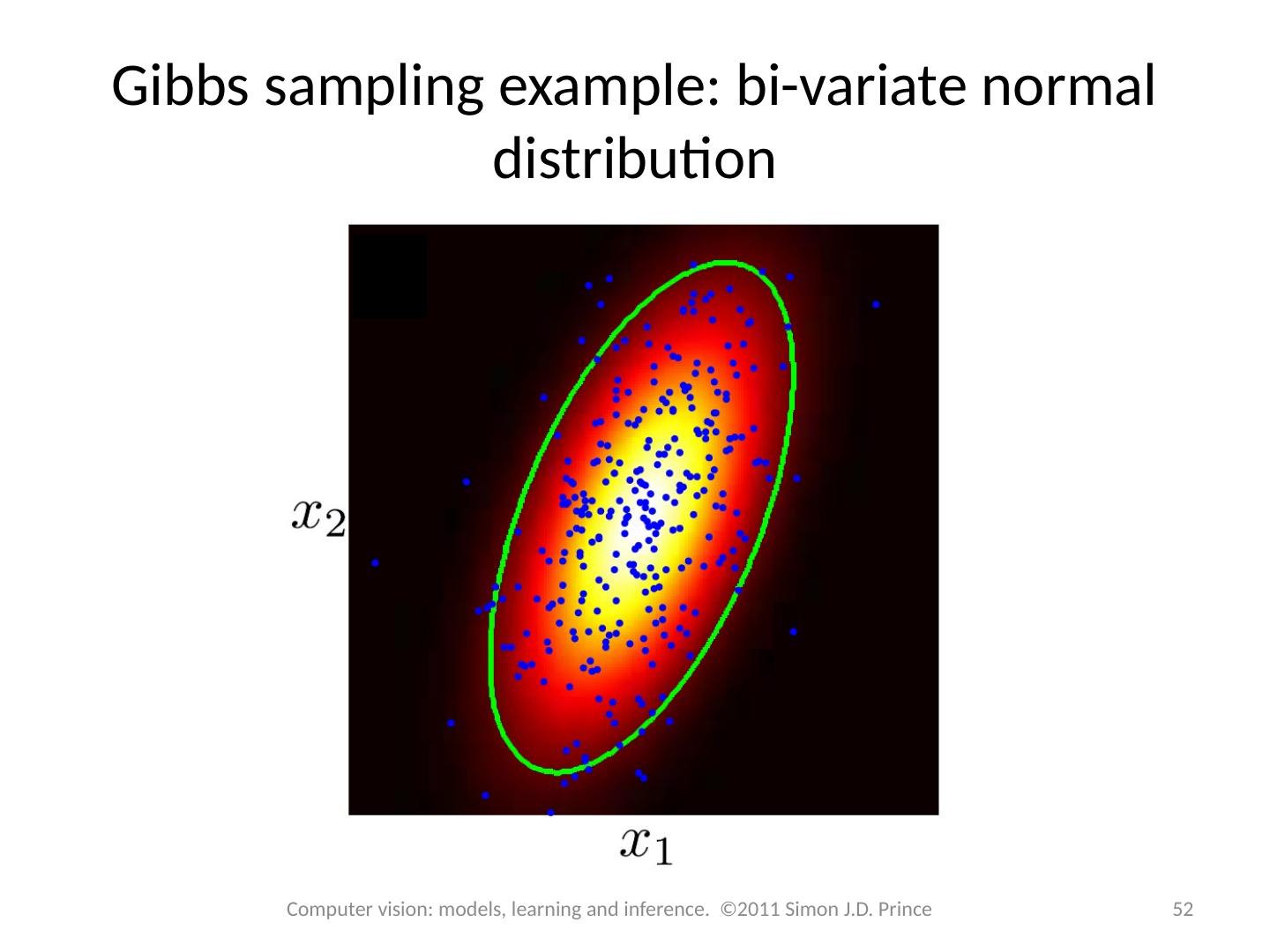
23 .Alternative form 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Can be written as Gibbs Distribution : Cost function (positive or negative) where
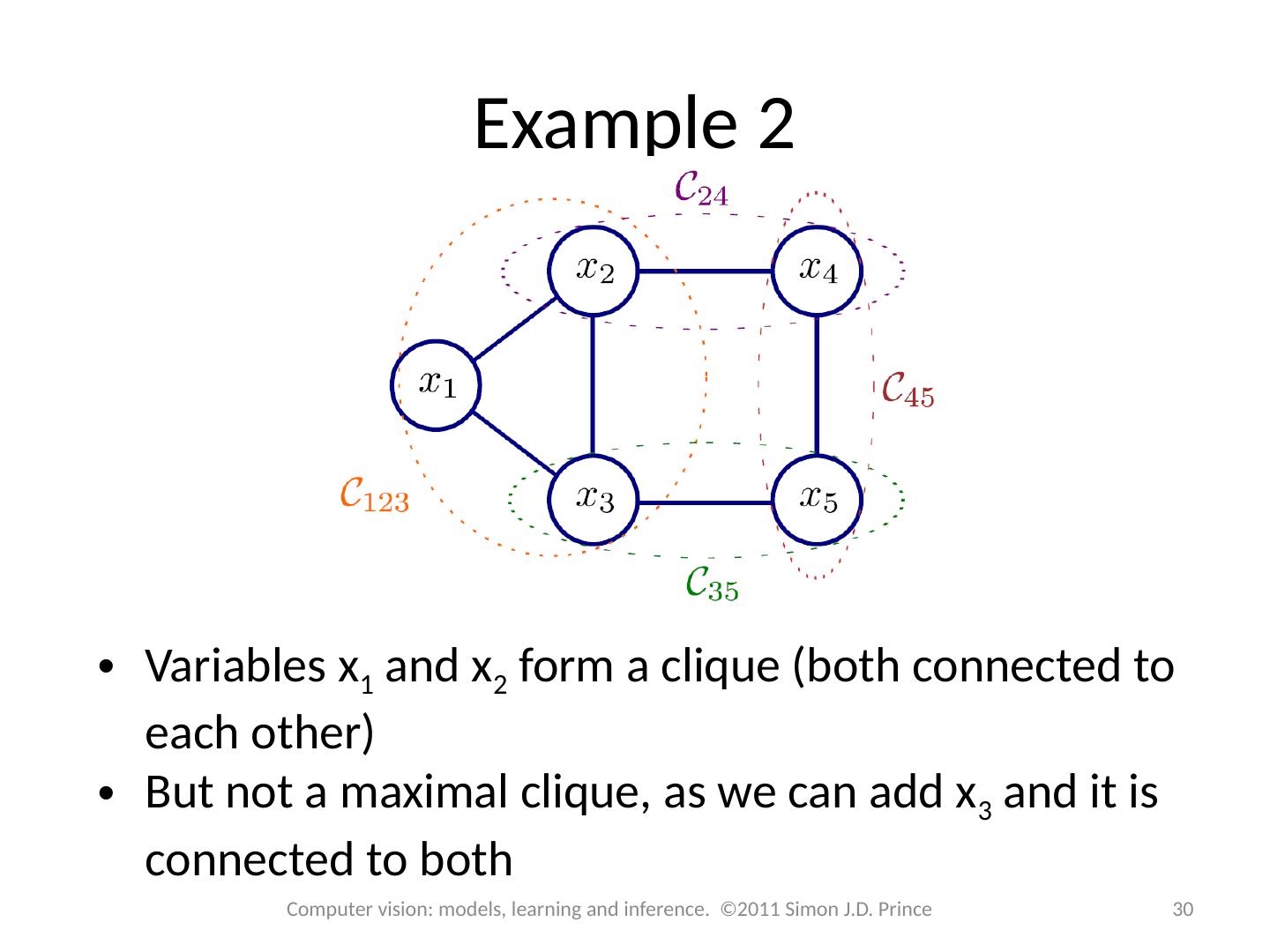
24 .Cliques 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Better to write undirected model as Product over cliques Clique Subset of variables
25 .Undirected graphical models 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince To visualize graphical model from factorization Sketch one node per random variable For every clique, sketch connection from every node to every other To extract factorization from graphical model Add one term to factorization per maximal clique (fully connected subset of nodes where it is not possible to add another node and remain fully connected)
26 .Conditional independence 26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Much simpler than for directed models: One set of nodes is conditionally independent of another given a third if the third set separates them (i.e. Blocks any path from the first node to the second)
27 .Example 1 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Represents factorization:
28 .Example 1 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince By inspection of graphical model: x 1 is conditionally independent of x 3 given x 2 , as the route from x 1 to x 3 is blocked by x 2 .
29 .Example 1 29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Algebraically: No dependence on x 3 implies that x 1 is conditionally independent of x 3 given x 2 .