09_Classification Models

1 .Computer vision: models, learning and inference Chapter 9 Classification Models

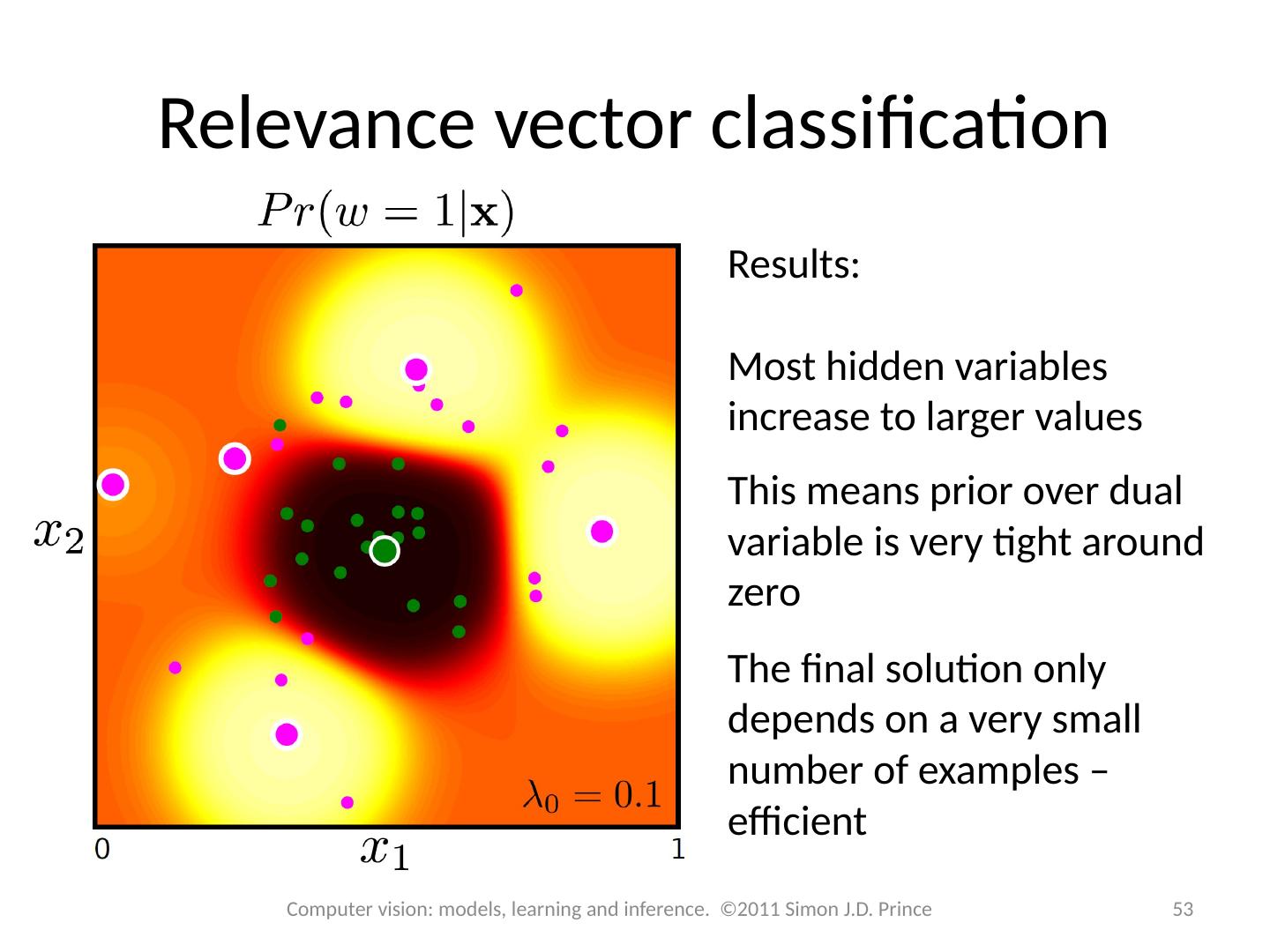
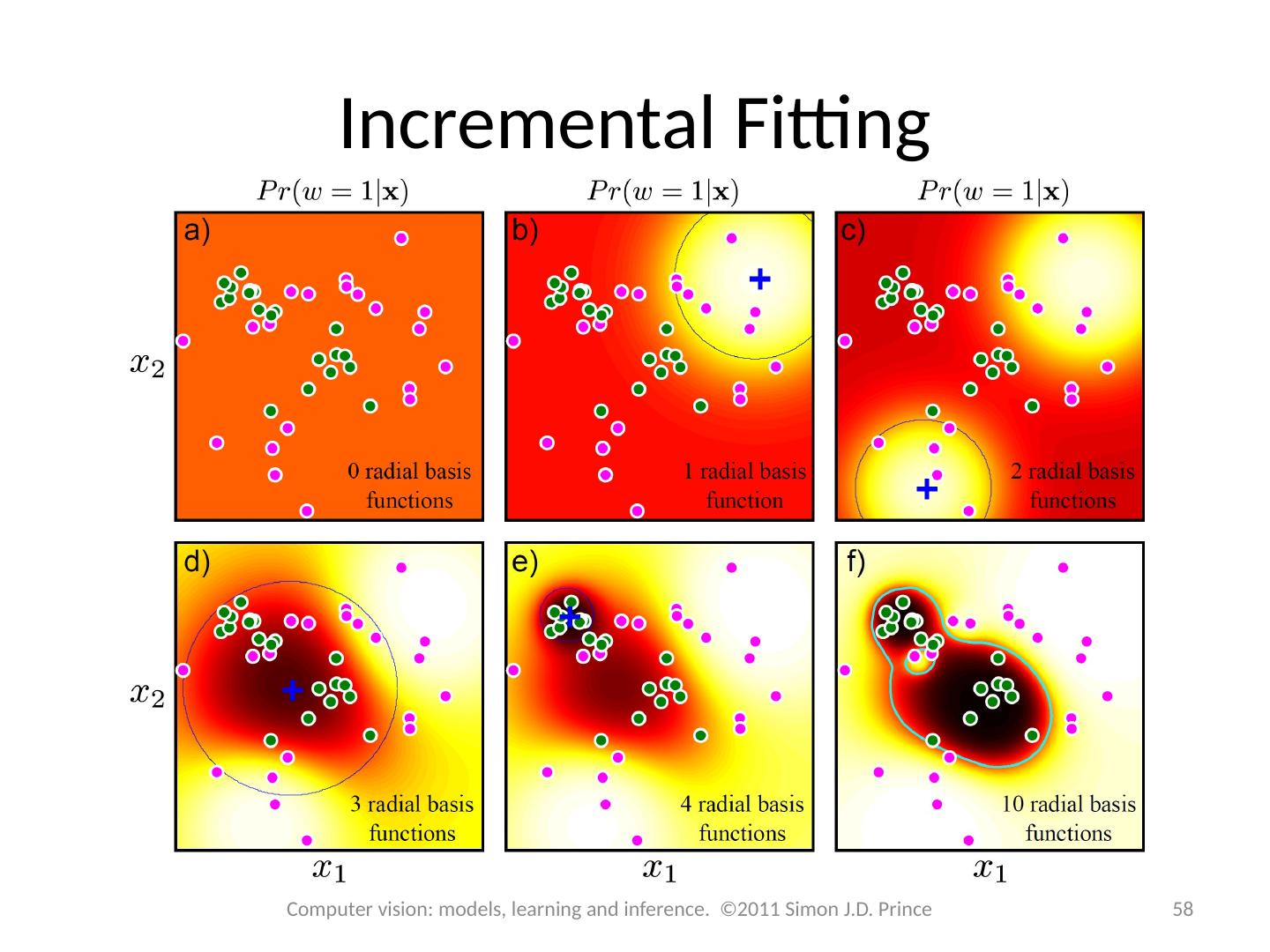
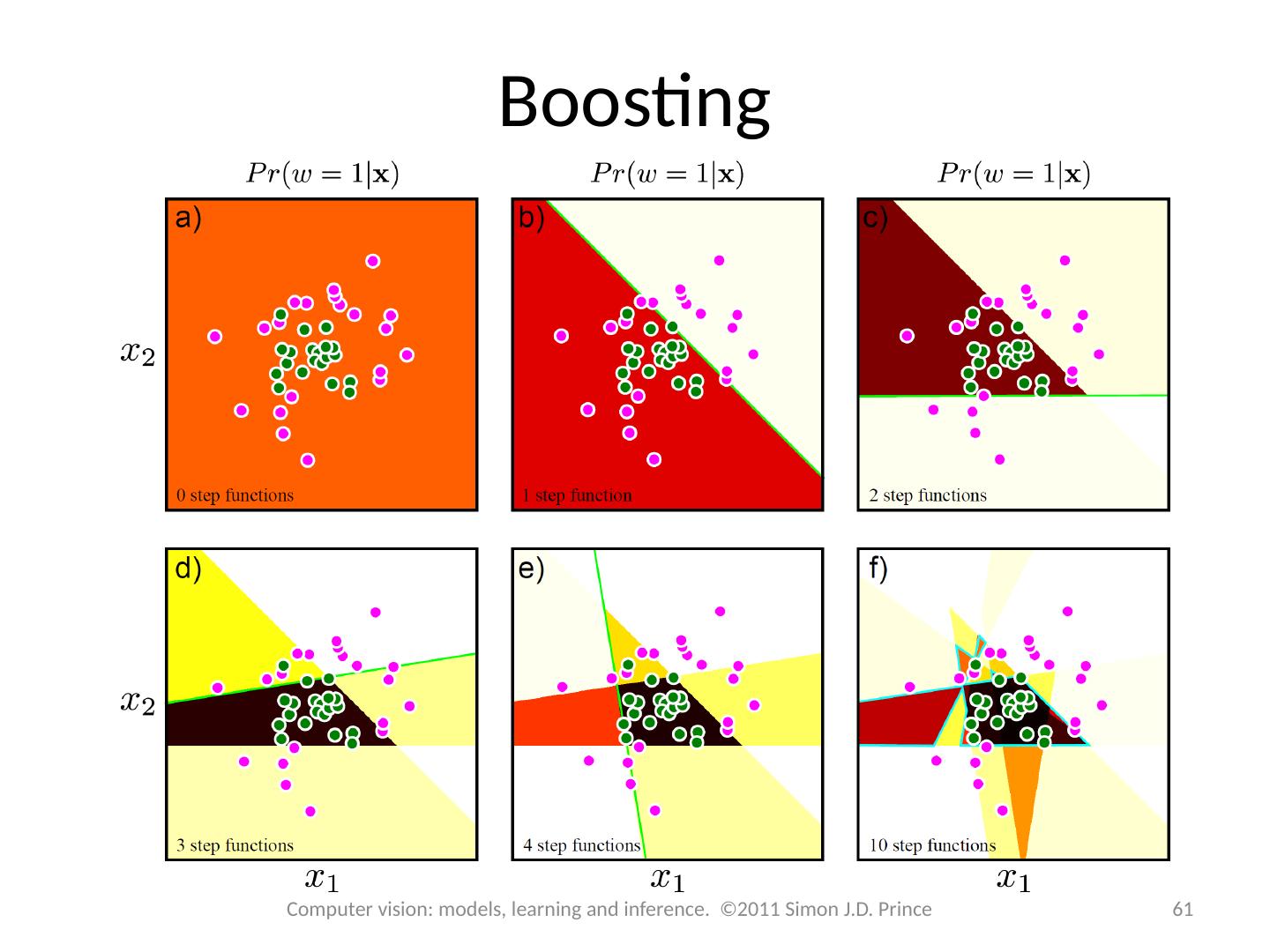
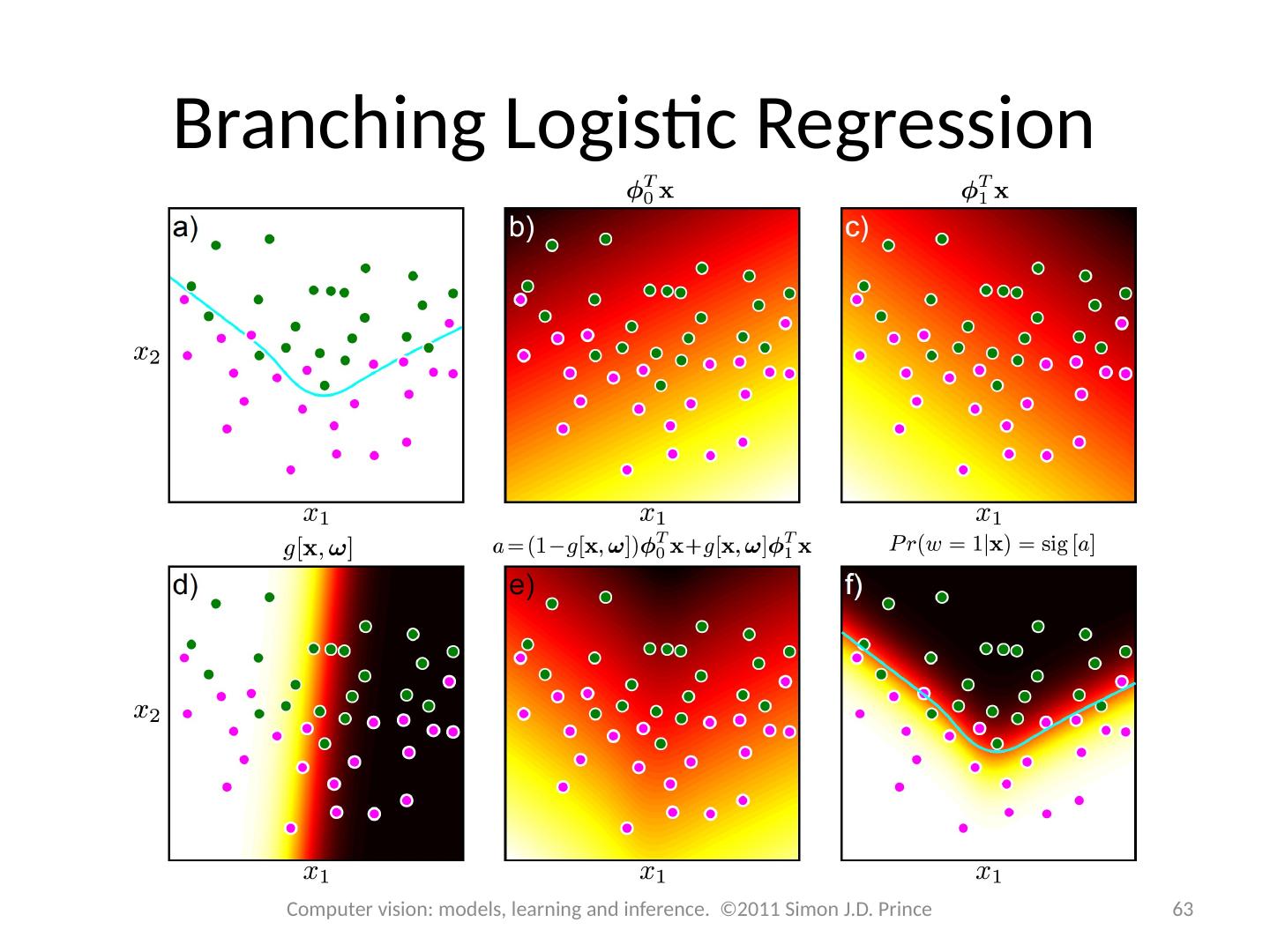
2 .Structure 2 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Logistic regression Bayesian logistic regression Non-linear logistic regression Kernelization and Gaussian process classification Incremental fitting, boosting and trees Multi-class classification Random classification trees Non-probabilistic classification Applications

3 .Models for machine vision 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

4 .Example application: Gender Classification 4 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

5 .Type 1: Model Pr( w | x ) - Discriminative How to model Pr( w | x )? Choose an appropriate form for Pr( w ) Make parameters a function of x Function takes parameters q that define its shape Learning algorithm : learn parameters q from training data x , w Inference algorithm : just evaluate Pr( w|x ) 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

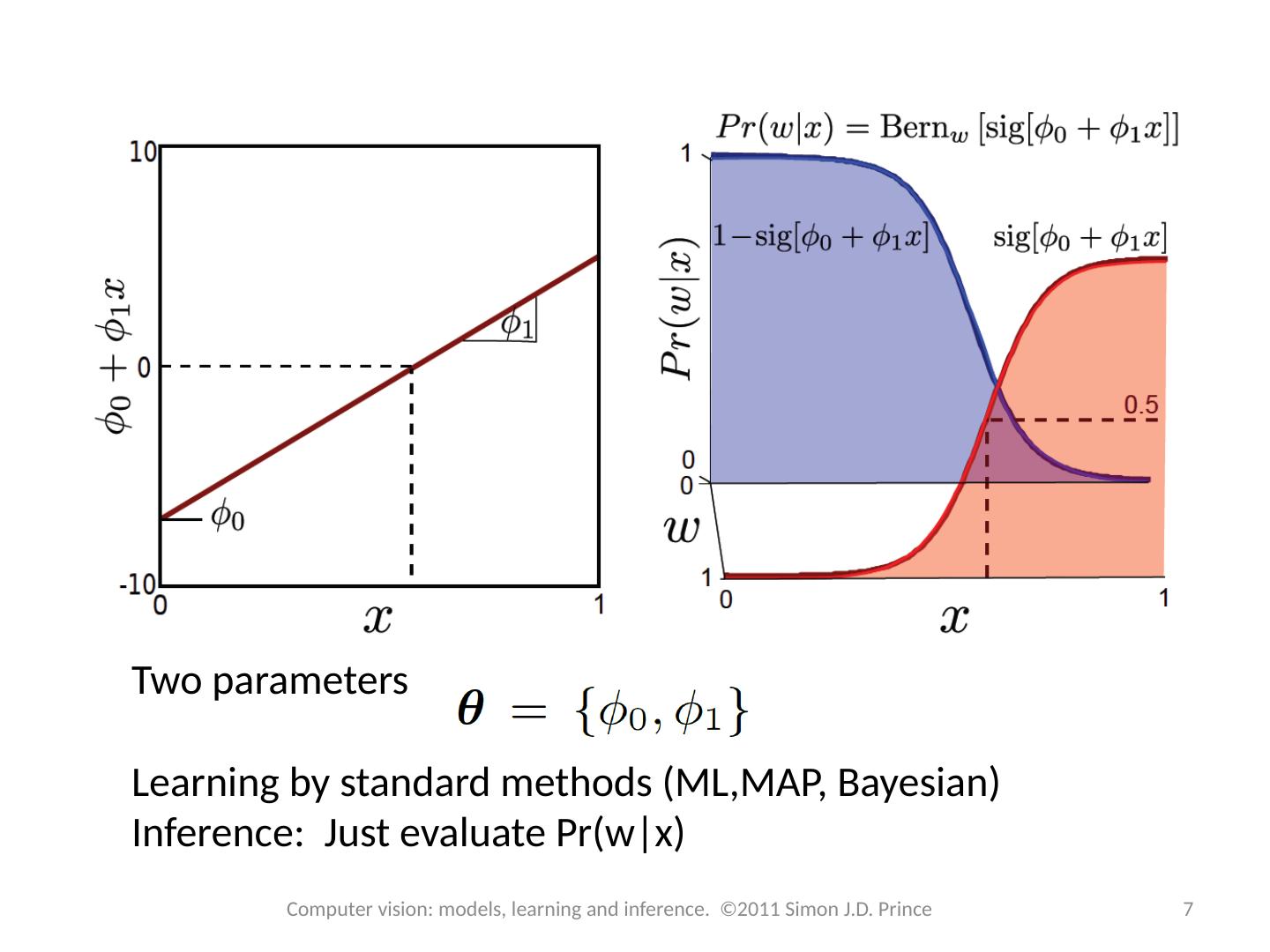
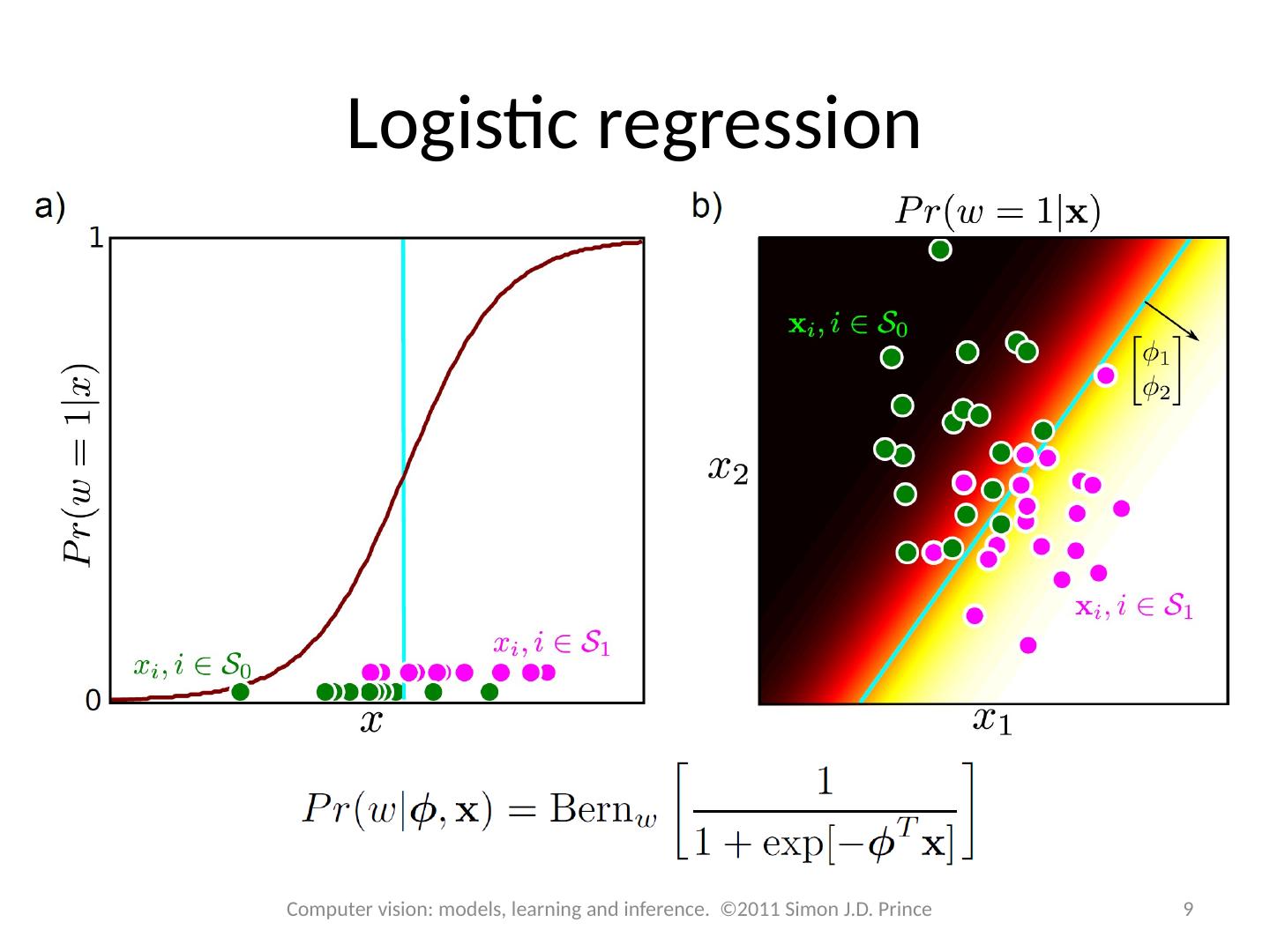
6 .Logistic Regression Consider two class problem. Choose Bernoulli distribution over world. Make parameter l a function of x Model activation with a linear function creates number between . Maps to with 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

7 .Two parameters Learning by standard methods (ML,MAP, Bayesian) Inference: Just evaluate Pr( w|x ) 7 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

8 .Neater Notation To make notation easier to handle, we Attach a 1 to the start of every data vector Attach the offset to the start of the gradient vector f New model: 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

9 .Logistic regression 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

10 .Maximum Likelihood 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Take logarithm Take derivative:

11 .Derivatives Unfortunately, there is no closed form solution– we cannot get an expression for f in terms of x and w Have to use a general purpose technique: “iterative non-linear optimization” 11 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

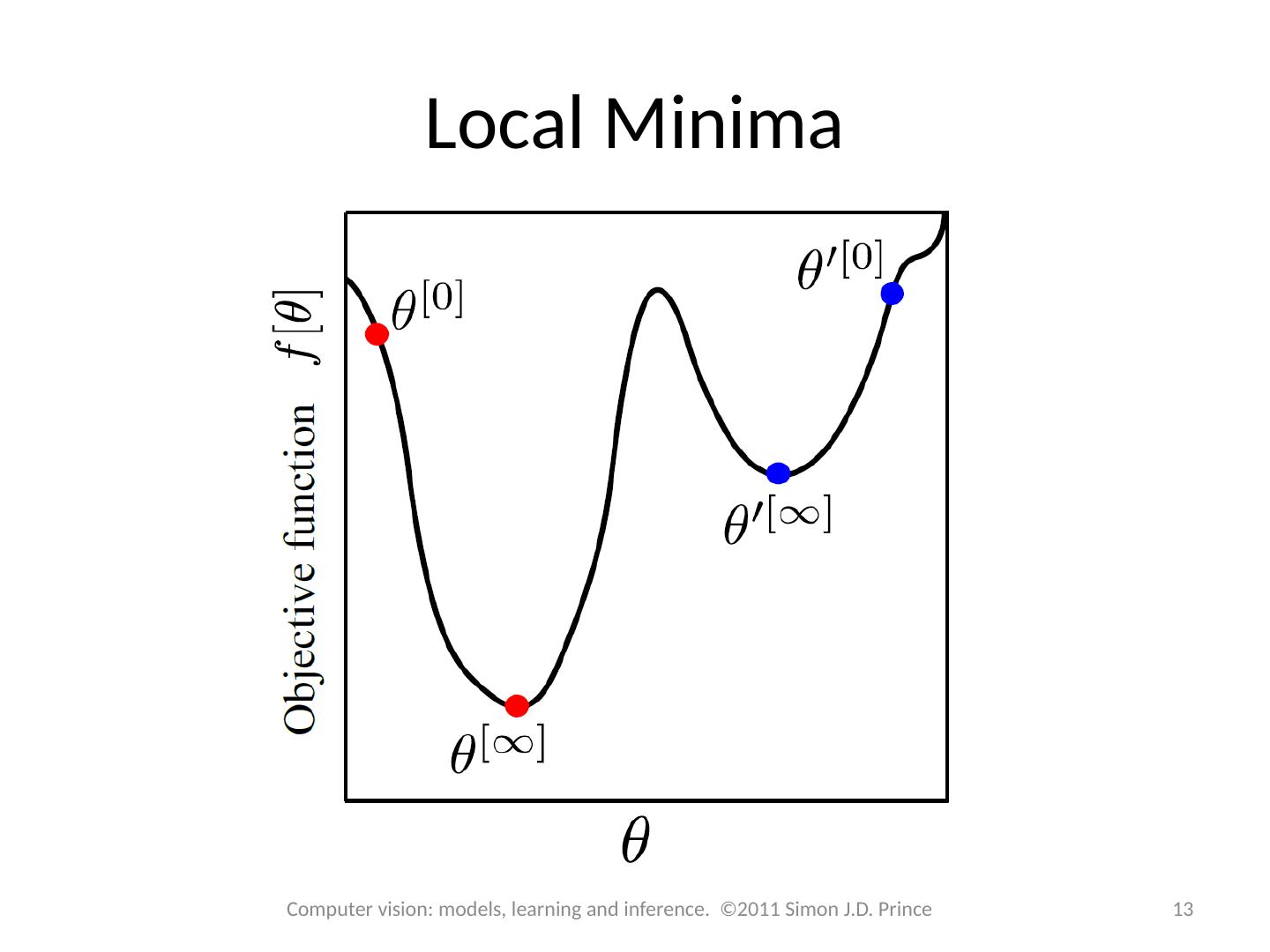
12 .Optimization Goal: How can we find the minimum? Basic idea: Start with estimate Take a series of small steps to Make sure that each step decreases cost When can’t improve, then must be at minimum Cost function or Objective function 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

13 .Local Minima 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

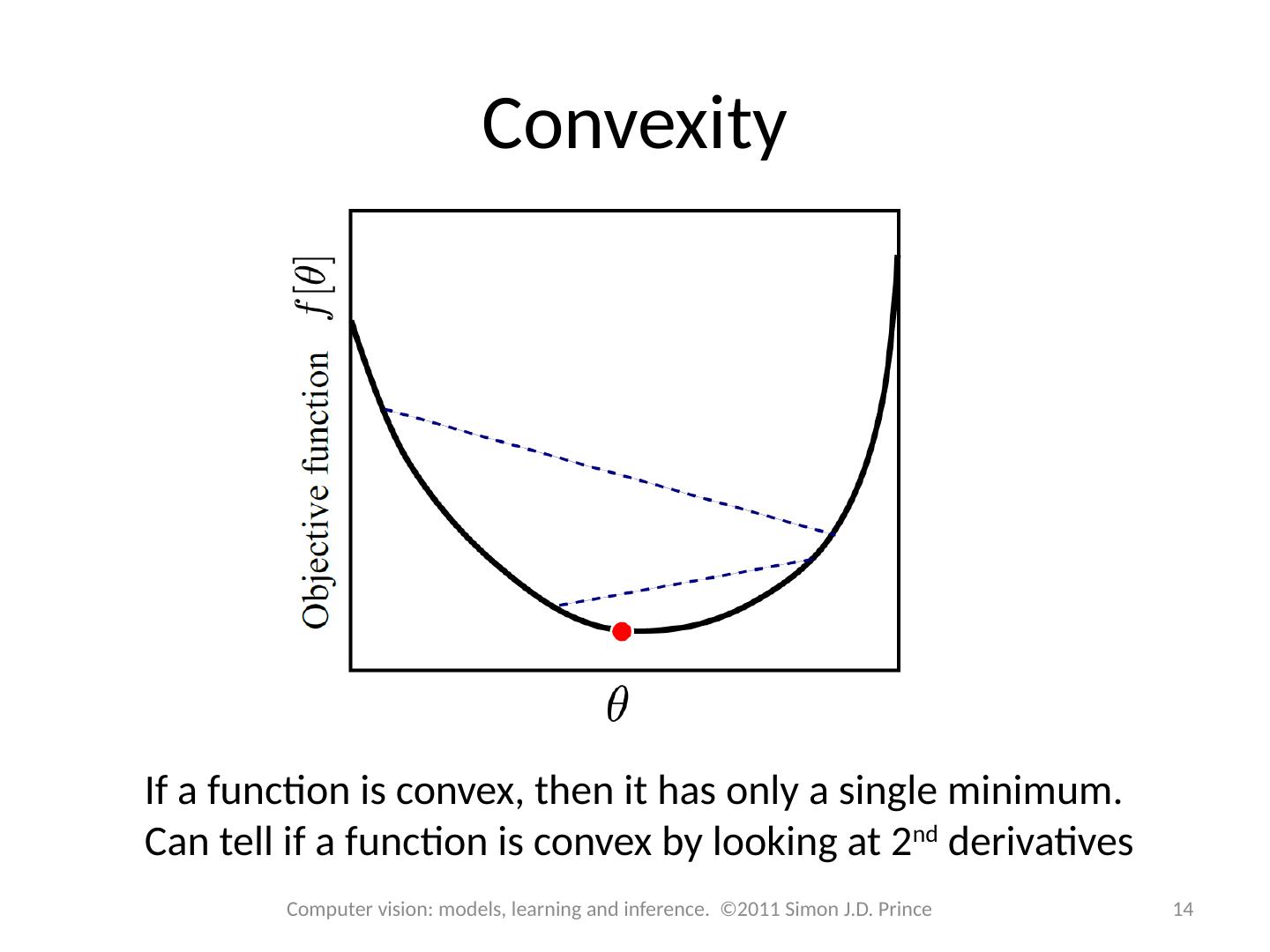
14 .Convexity If a function is convex, then it has only a single minimum. Can tell if a function is convex by looking at 2 nd derivatives 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

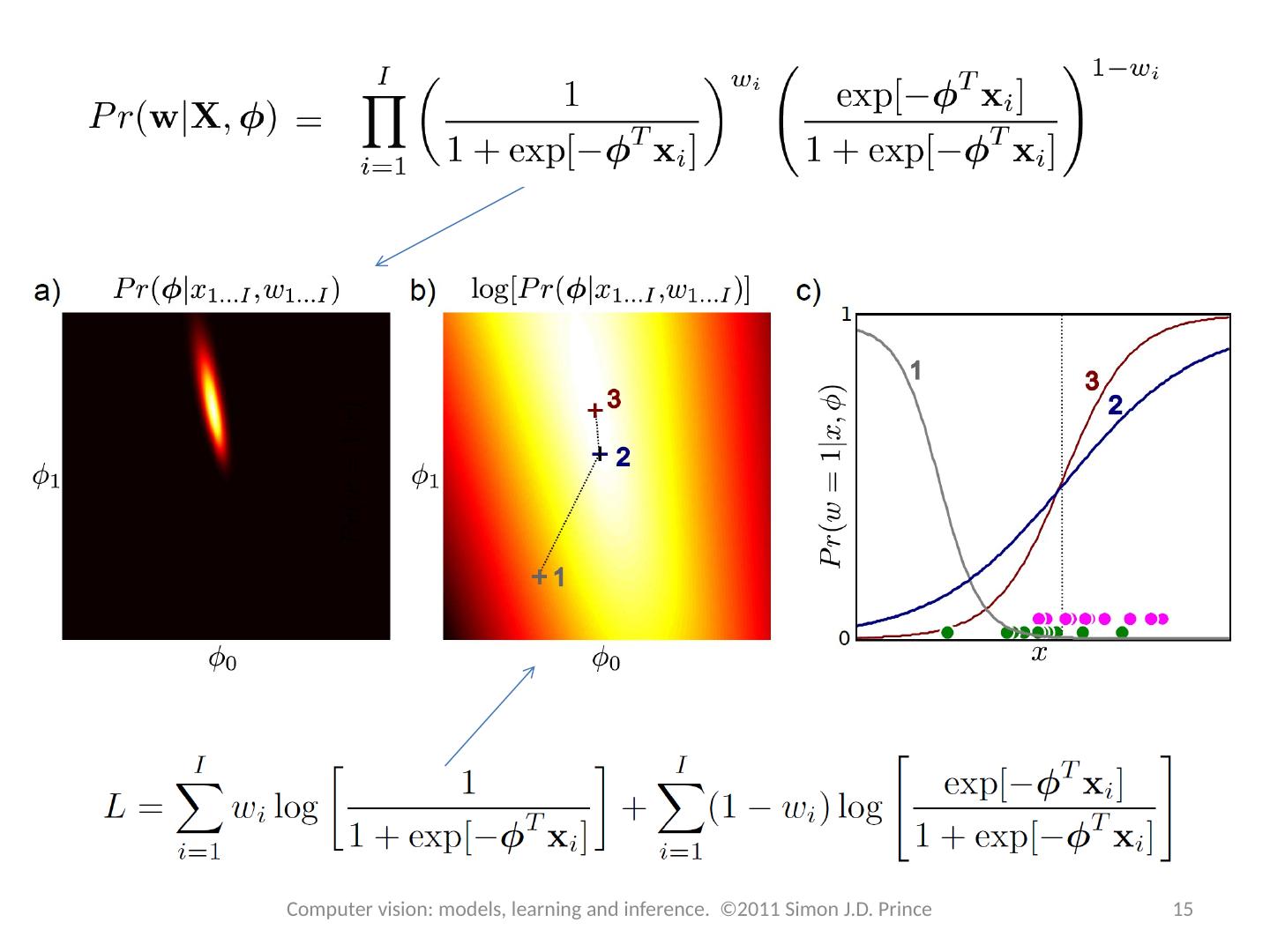
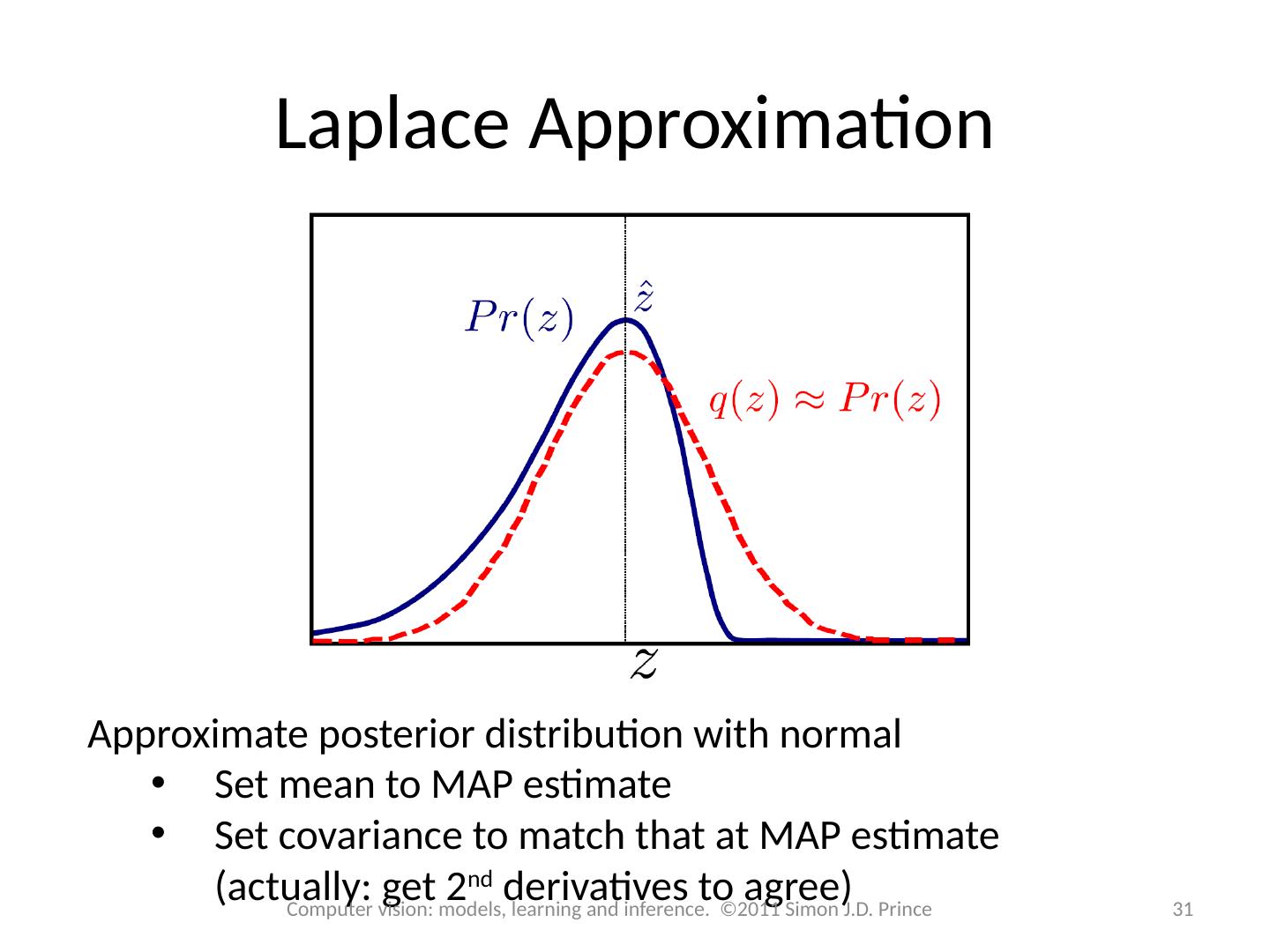
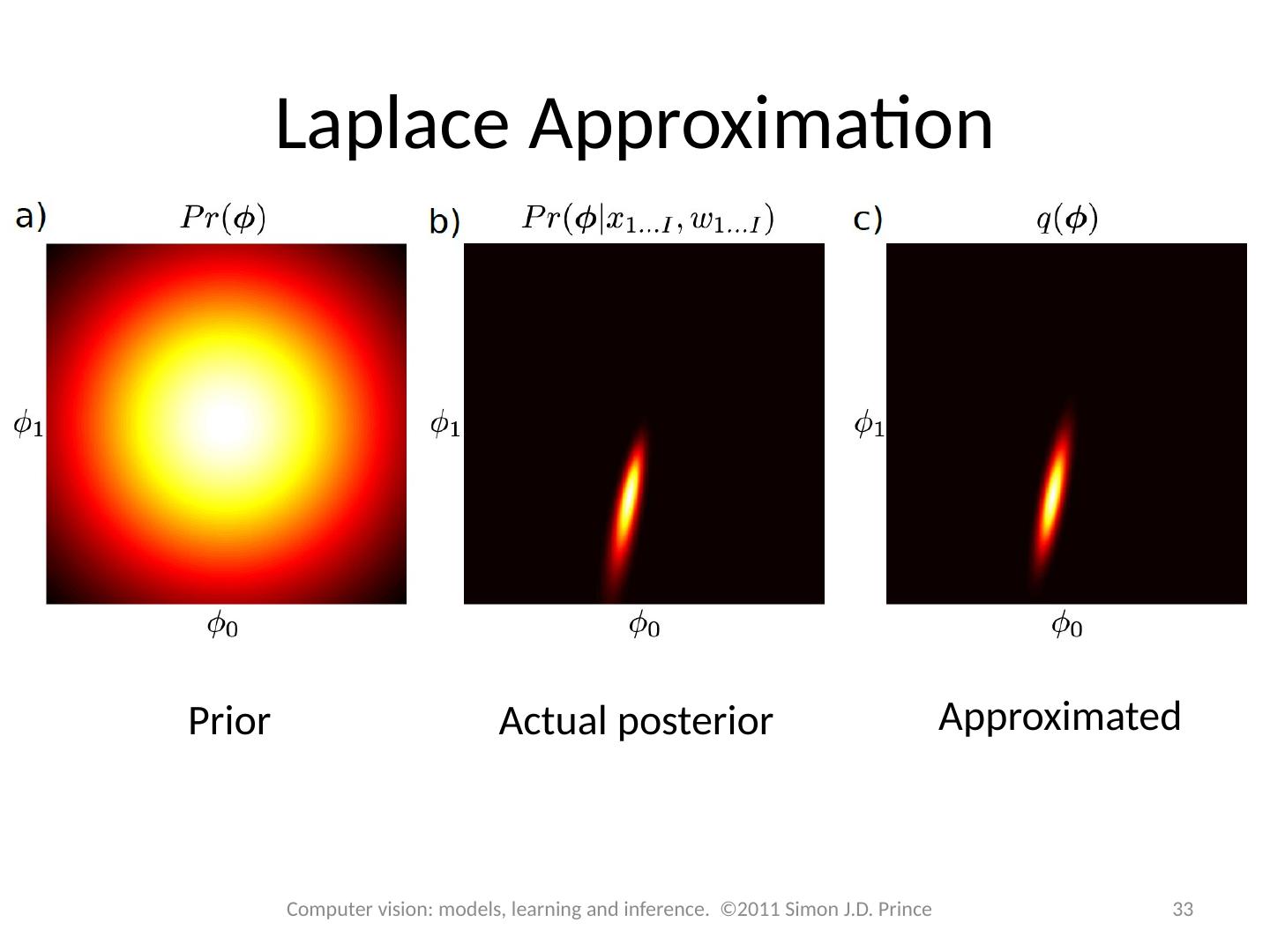
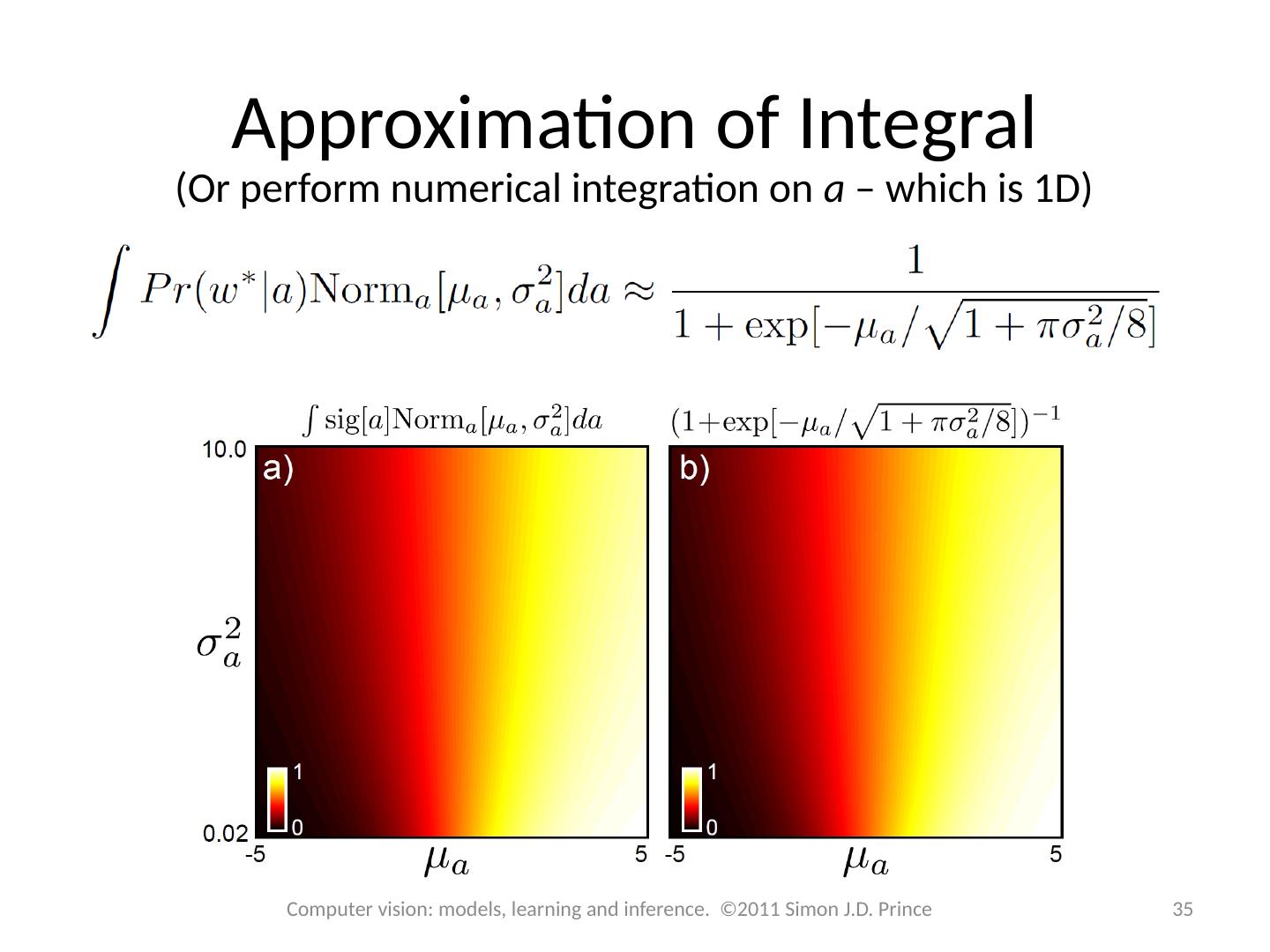
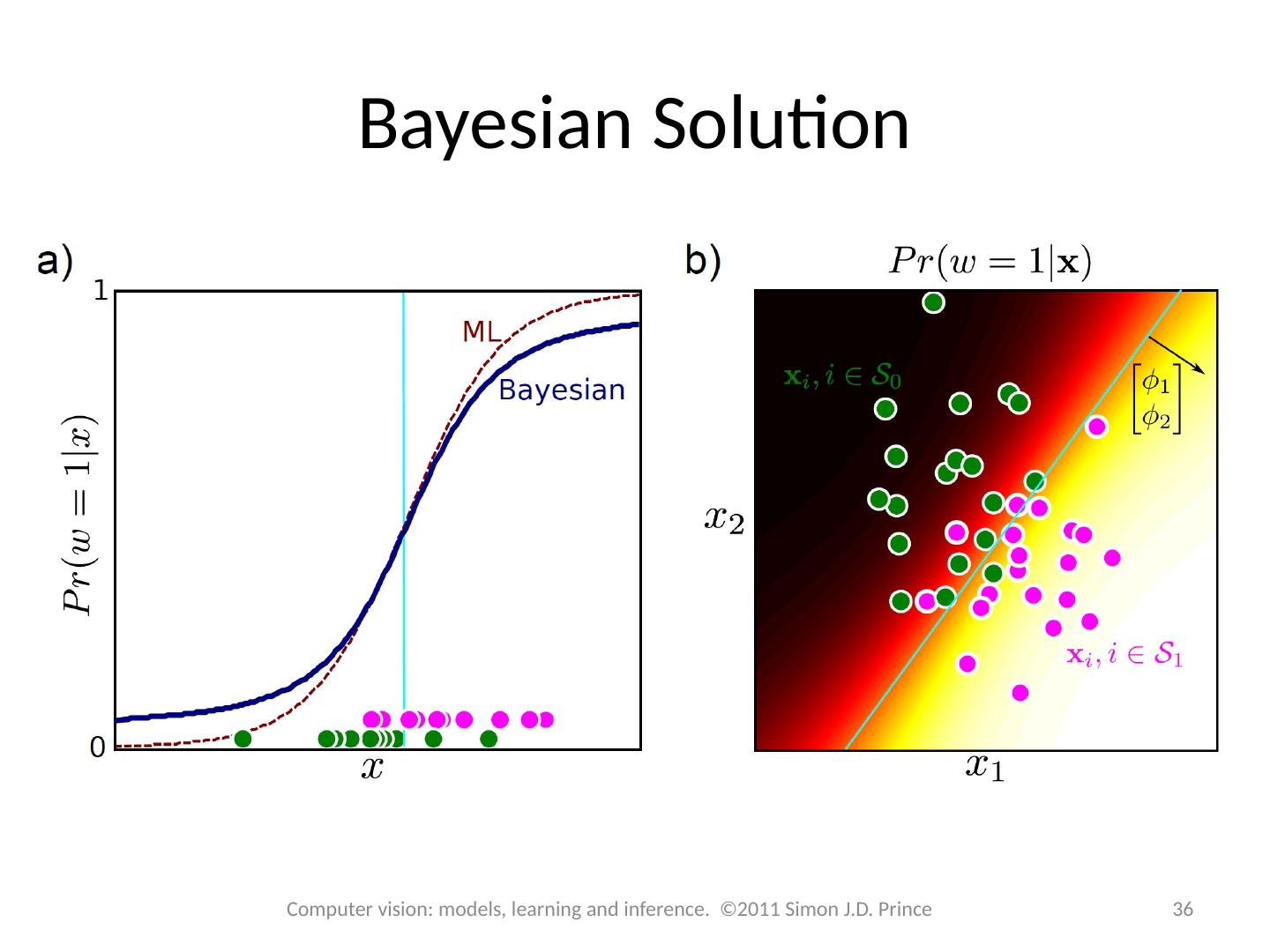
15 .15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

16 .Gradient Based Optimization Choose a search direction s based on the local properties of the function Perform an intensive search along the chosen direction. This is called line search Then set 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

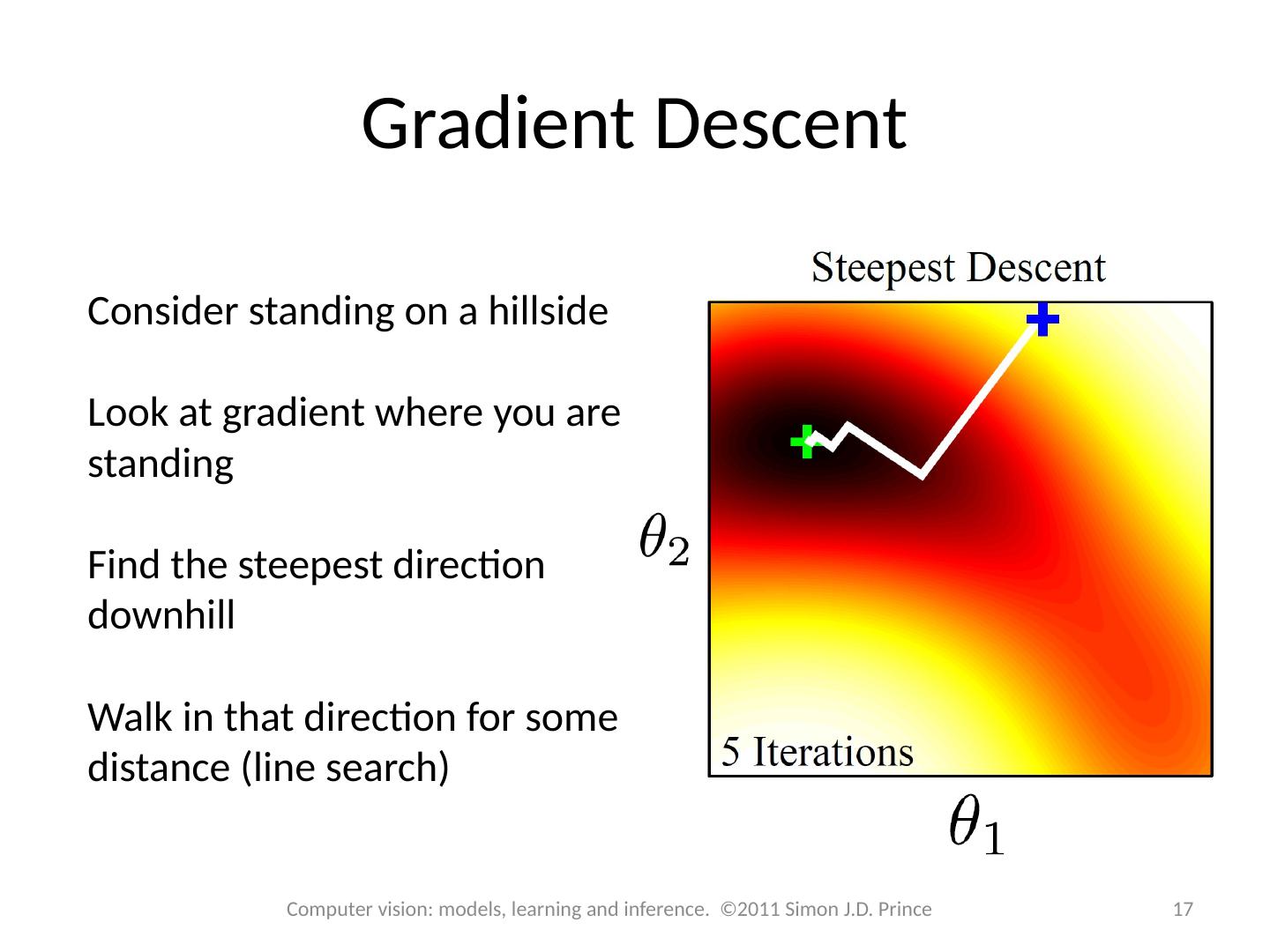
17 .Gradient Descent Consider standing on a hillside Look at gradient where you are standing Find the steepest direction downhill Walk in that direction for some distance (line search) 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

18 .Finite differences What if we can’t compute the gradient? Compute finite difference approximation: where e j is the unit vector in the j th direction 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

19 .Steepest Descent Problems Close up 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

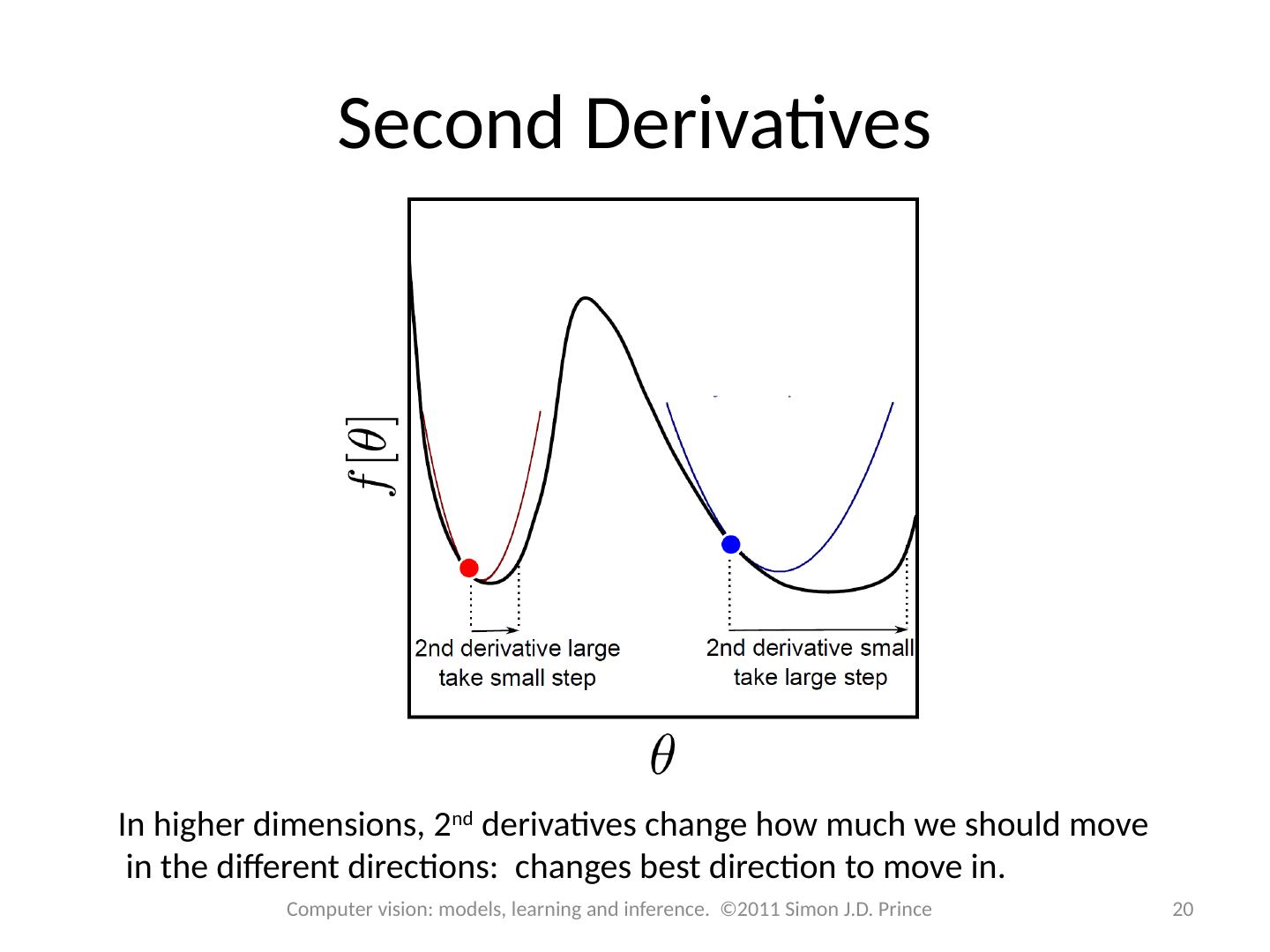
20 .Second Derivatives In higher dimensions, 2 nd derivatives change how much we should move in the different directions: changes best direction to move in. 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

21 .Newton’s Method Approximate function with Taylor expansion Take derivative Re-arrange 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Adding line search (derivatives taken at time t )

22 .Newton’s Method Matrix of second derivatives is called the Hessian. Expensive to compute via finite differences. If positive definite, then convex 22 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

23 .Newton vs. Steepest Descent 23 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

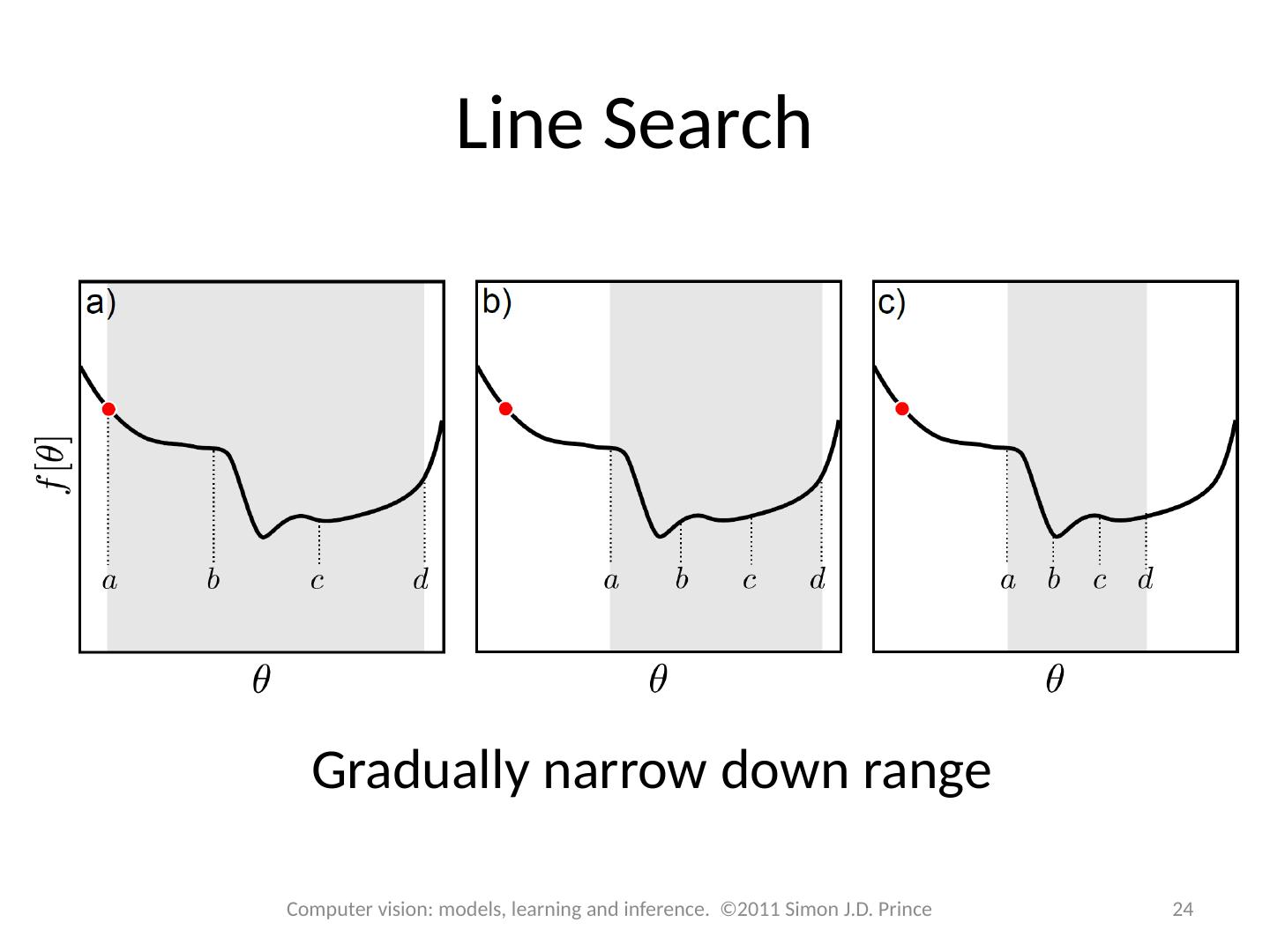
24 .Line Search Gradually narrow down range 24 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

25 .Optimization for Logistic Regression Derivatives of log likelihood: Positive definite! 25 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

26 .26 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

27 .Maximum likelihood fits 27 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

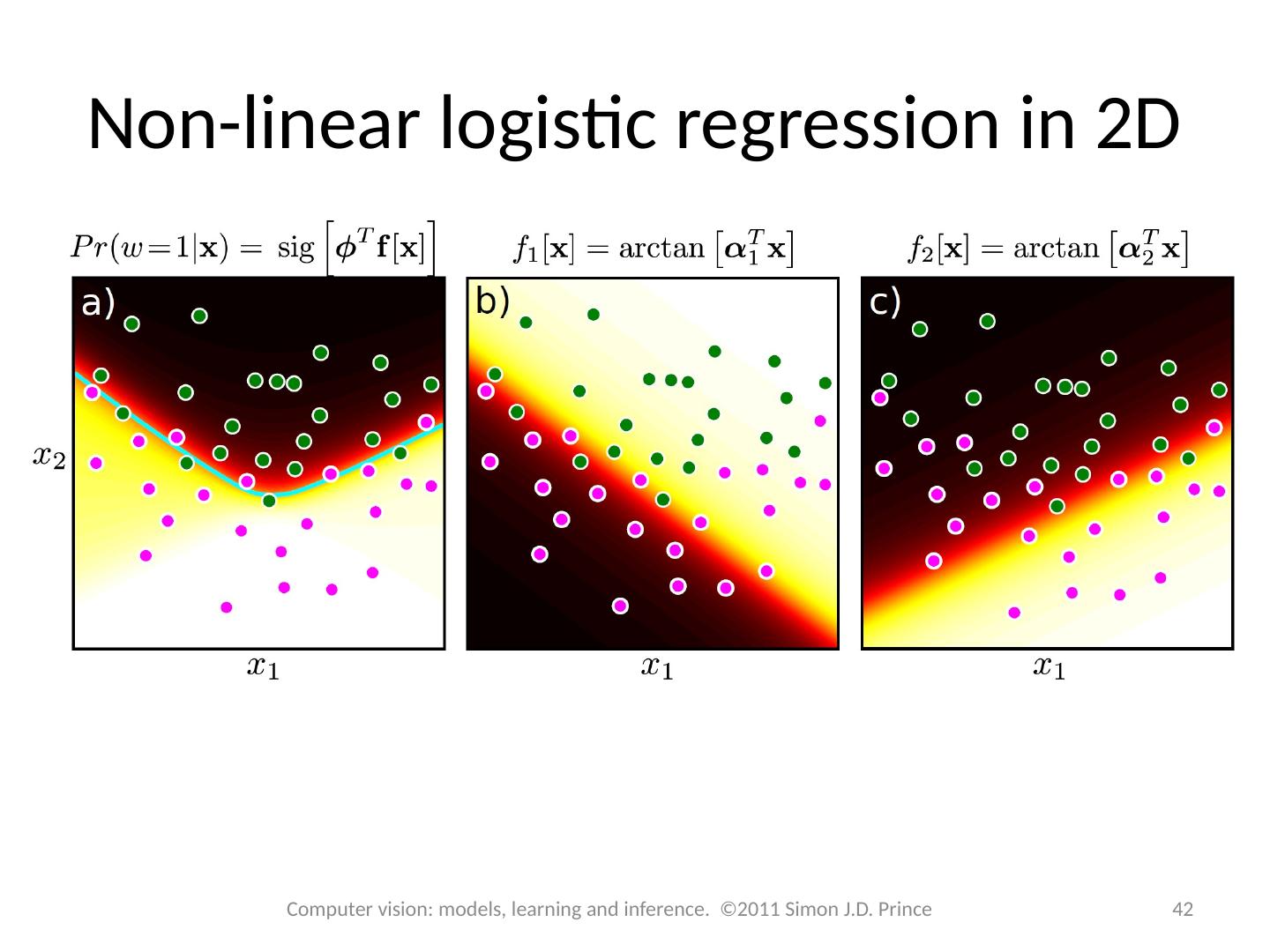
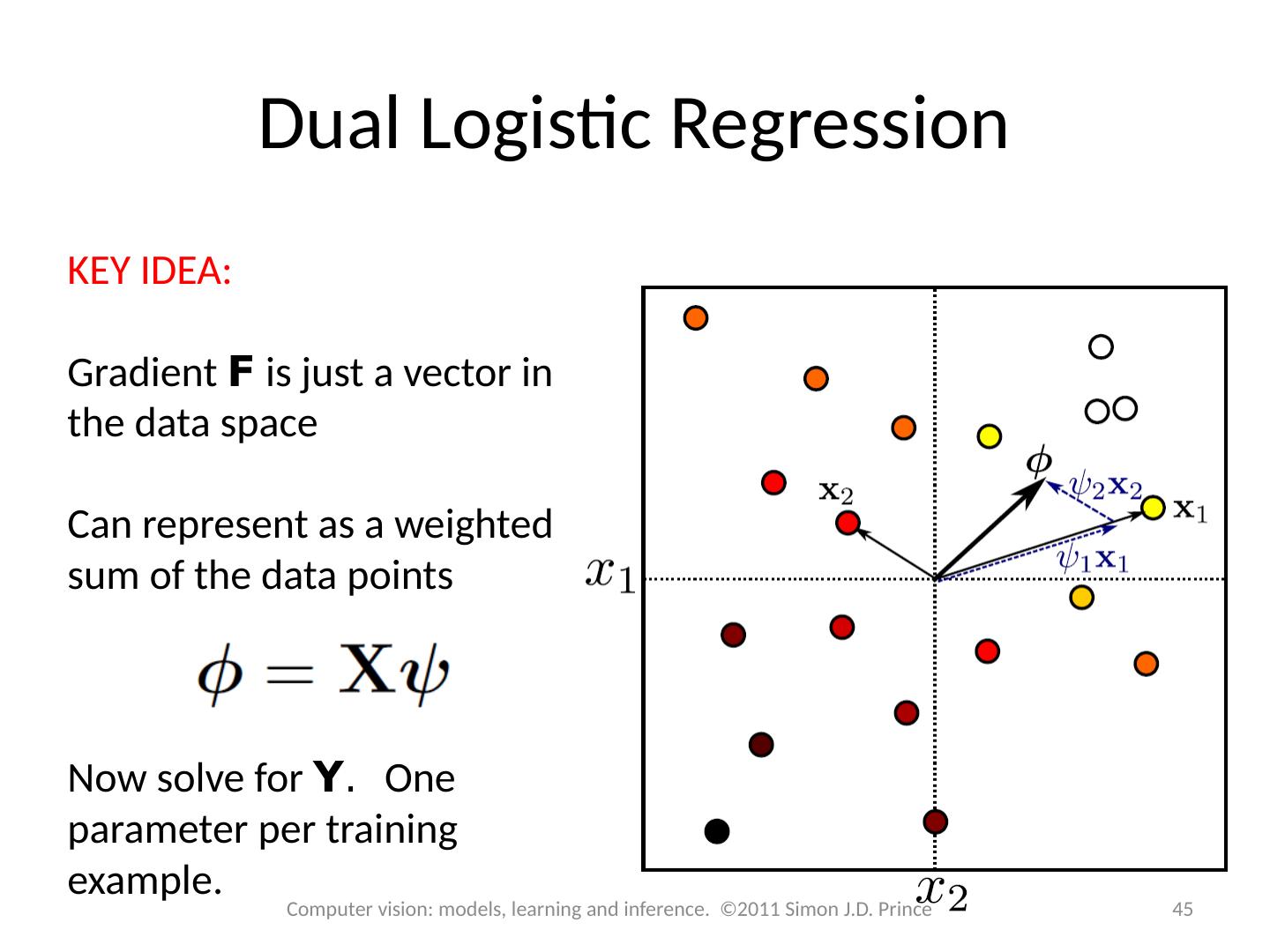
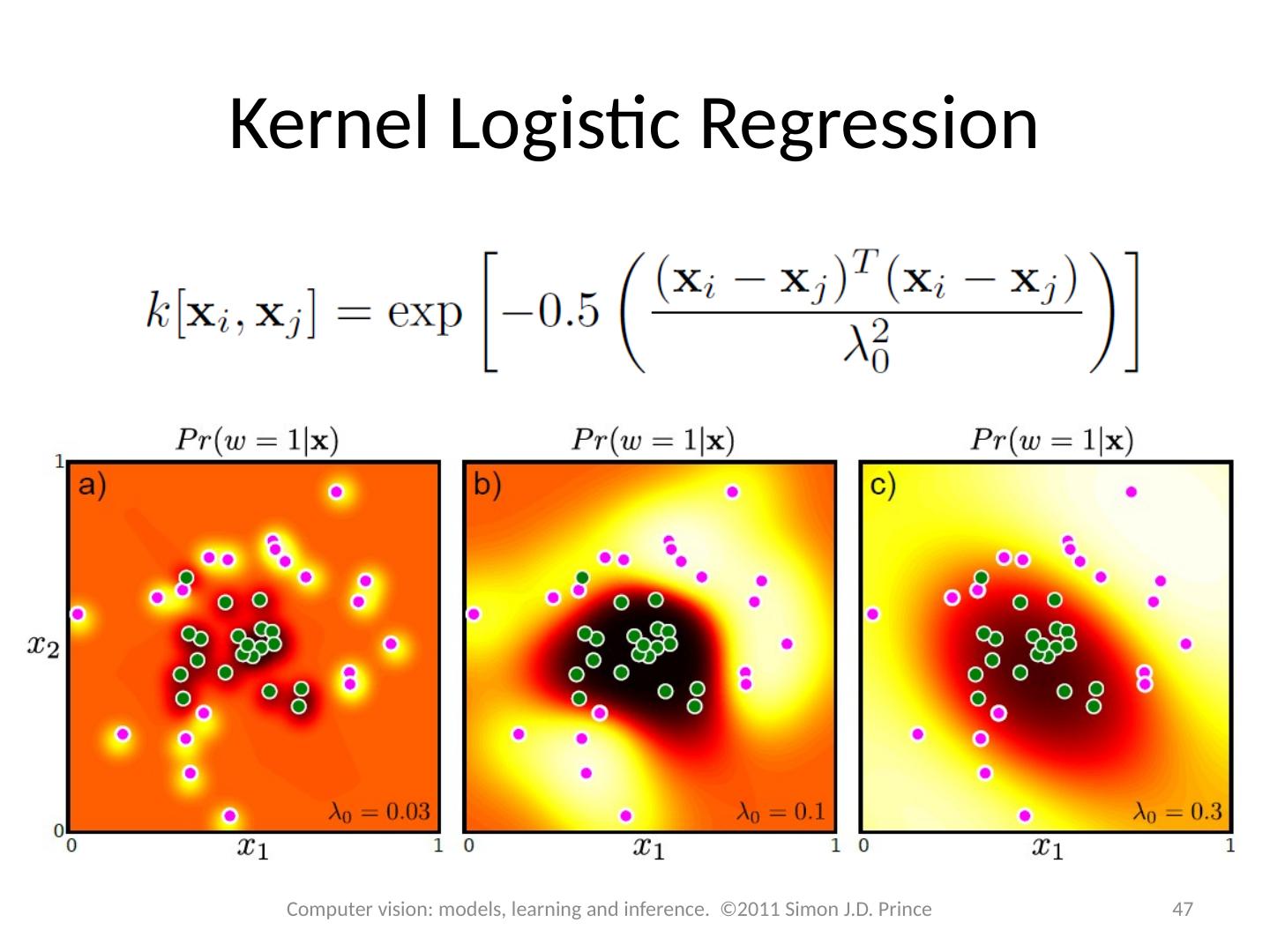
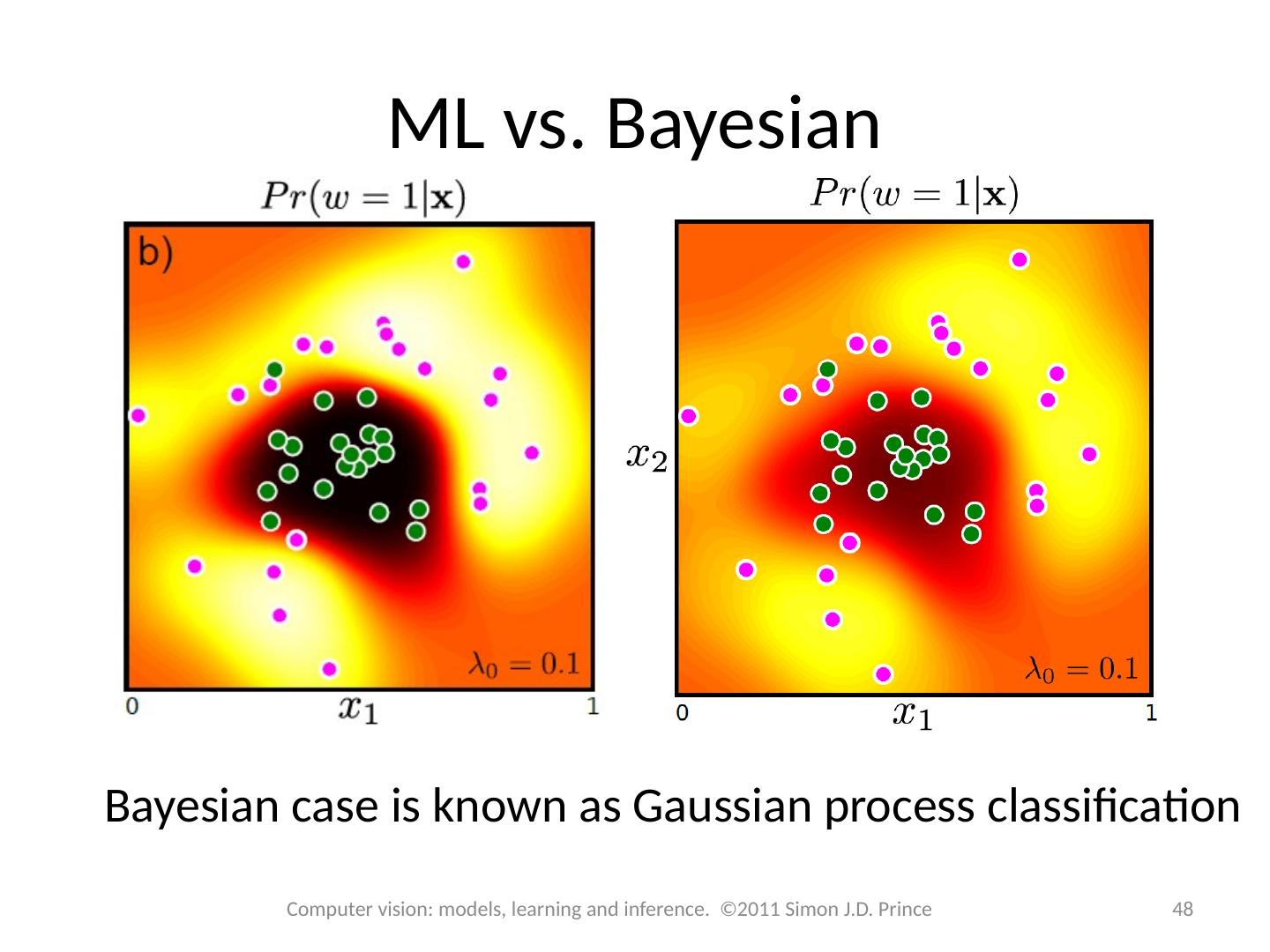
28 .Structure 28 28 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Logistic regression Bayesian logistic regression Non-linear logistic regression Kernelization and Gaussian process classification Incremental fitting, boosting and trees Multi-class classification Random classification trees Non-probabilistic classification Applications

29 .29 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince