05_Normal_Distribution

1 .Computer vision: models, learning and inference Chapter 5 The Normal Distribution

2 .Univariate Normal Distribution For short we write: Univariate normal distribution describes single continuous variable. Takes 2 parameters m and s 2 >0 2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

3 .Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Multivariate Normal Distribution For short we write: Multivariate normal distribution describes multiple continuous variables. Takes 2 parameters a vector containing mean position, m a symmetric “positive definite” covariance matrix S Positive definite: is positive for any real 3

4 .Types of covariance Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 4 Symmetric

5 .Diagonal Covariance = Independence Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 5

6 .Consider green frame of reference: Relationship between pink and green frames of reference: Substituting in: Conclusion: Full covariance can be decomposed into rotation matrix and diagonal Decomposition of Covariance Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 6

7 .Transformation of Variables If and we transform the variable as The result is also a normal distribution: Can be used to generate data from arbitrary Gaussians from standard one Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 7

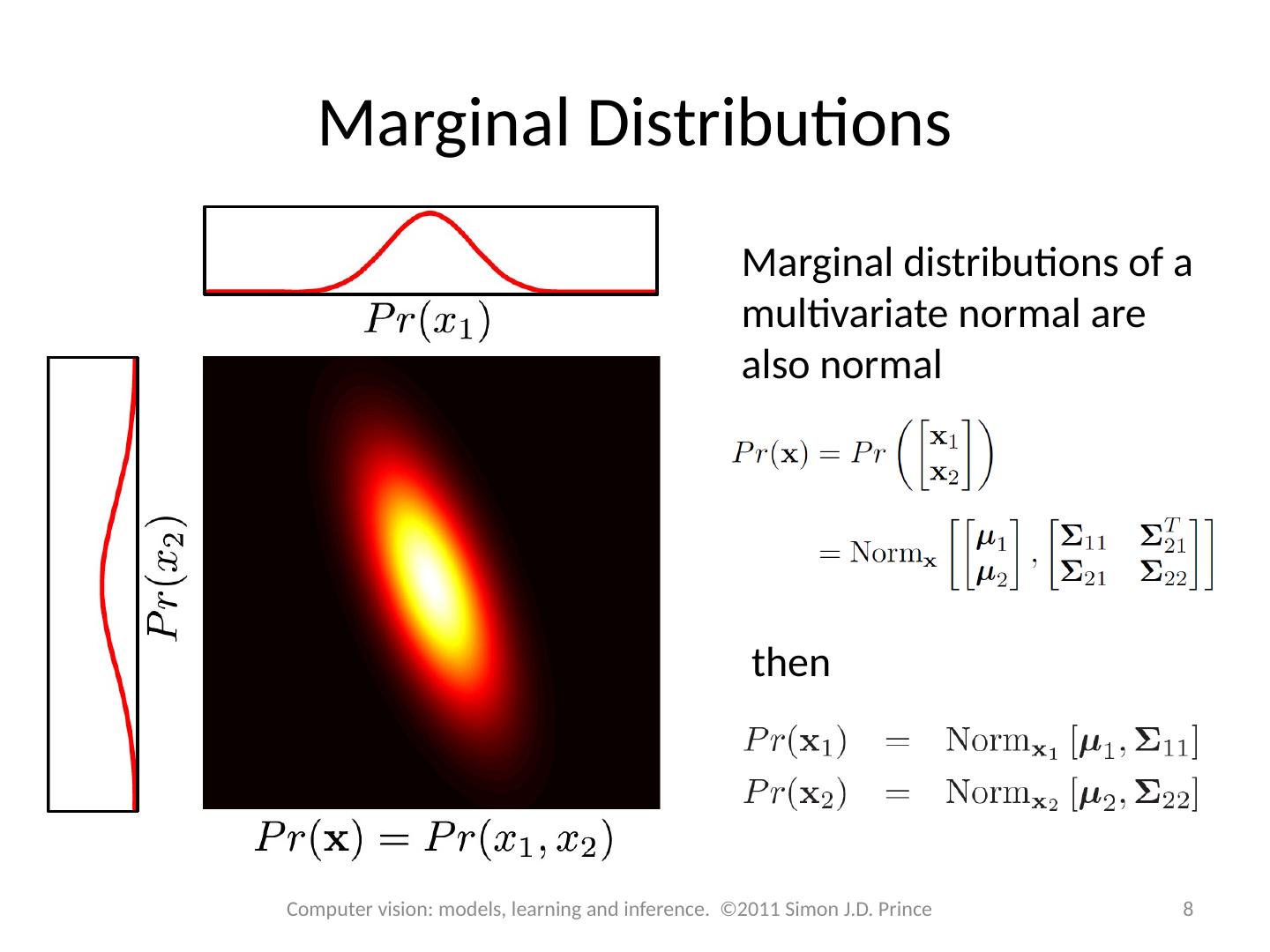
8 .Marginal Distributions Marginal distributions of a multivariate normal are also normal If then Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 8

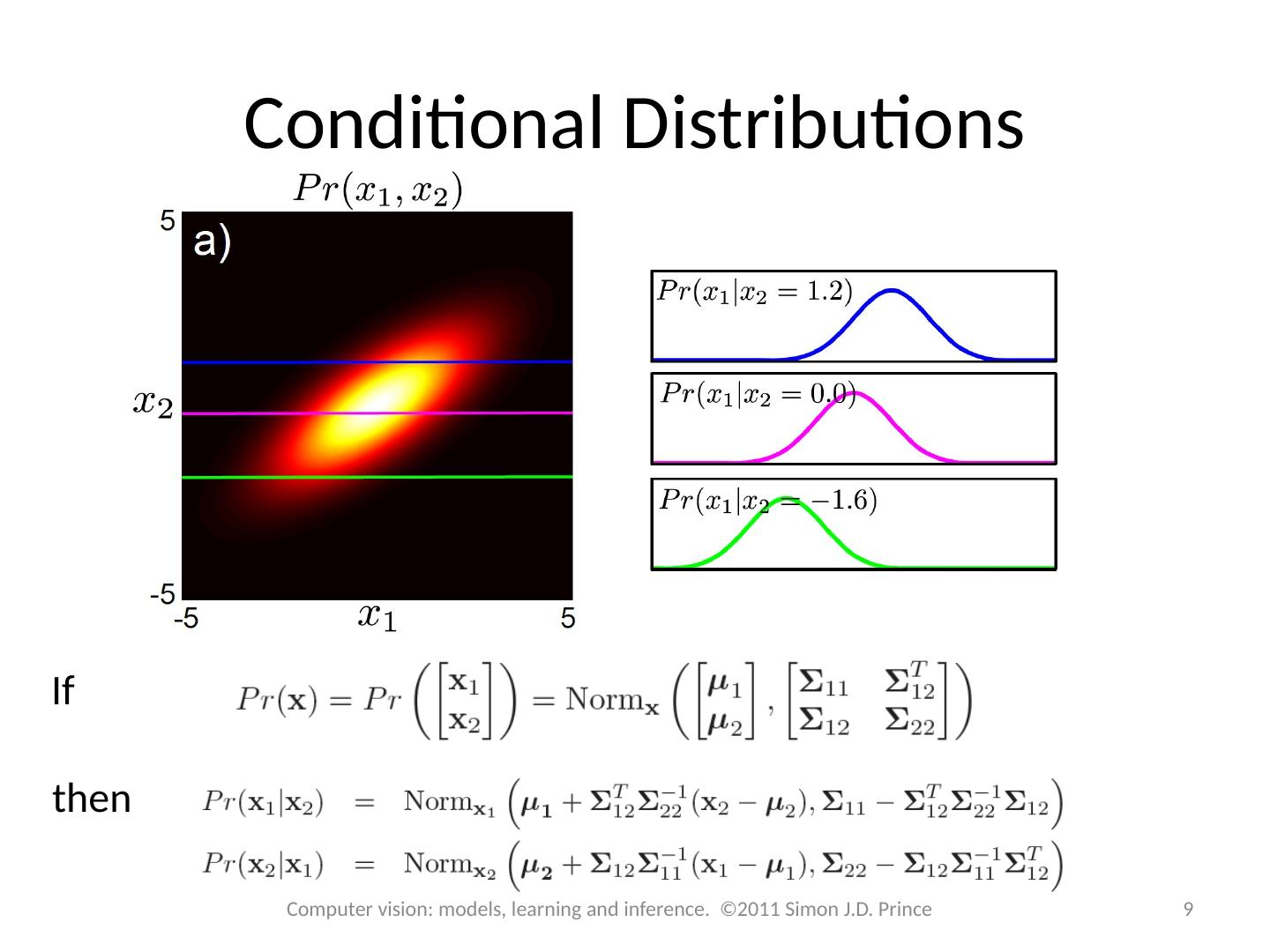
9 .Conditional Distributions If then Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 9

10 .Conditional Distributions Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 10 For spherical / diagonal case, x 1 and x 2 are independent so all of the conditional distributions are the same.

11 .Product of two normals (self- conjugacy w.r.t mean) The product of any two normal distributions in the same variable is proportional to a third normal distribution Amazingly, the constant also has the form of a normal! Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 11

12 .Change of Variables where If the mean of a normal in x is proportional to y then this can be re-expressed as a normal in y that is proportional to x Computer vision: models, learning and inference. ©2011 Simon J.D. Prince 12

13 .Conclusion 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Normal distribution is used ubiquitously in computer vision Important properties: Marginal dist. of normal is normal Conditional dist. of normal is normal Product of normals prop. to normal Normal under linear change of variables