03_Probability_Distributions

1 .Computer vision: models, learning and inference Chapter 3 Common probability distributions

2 .2 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

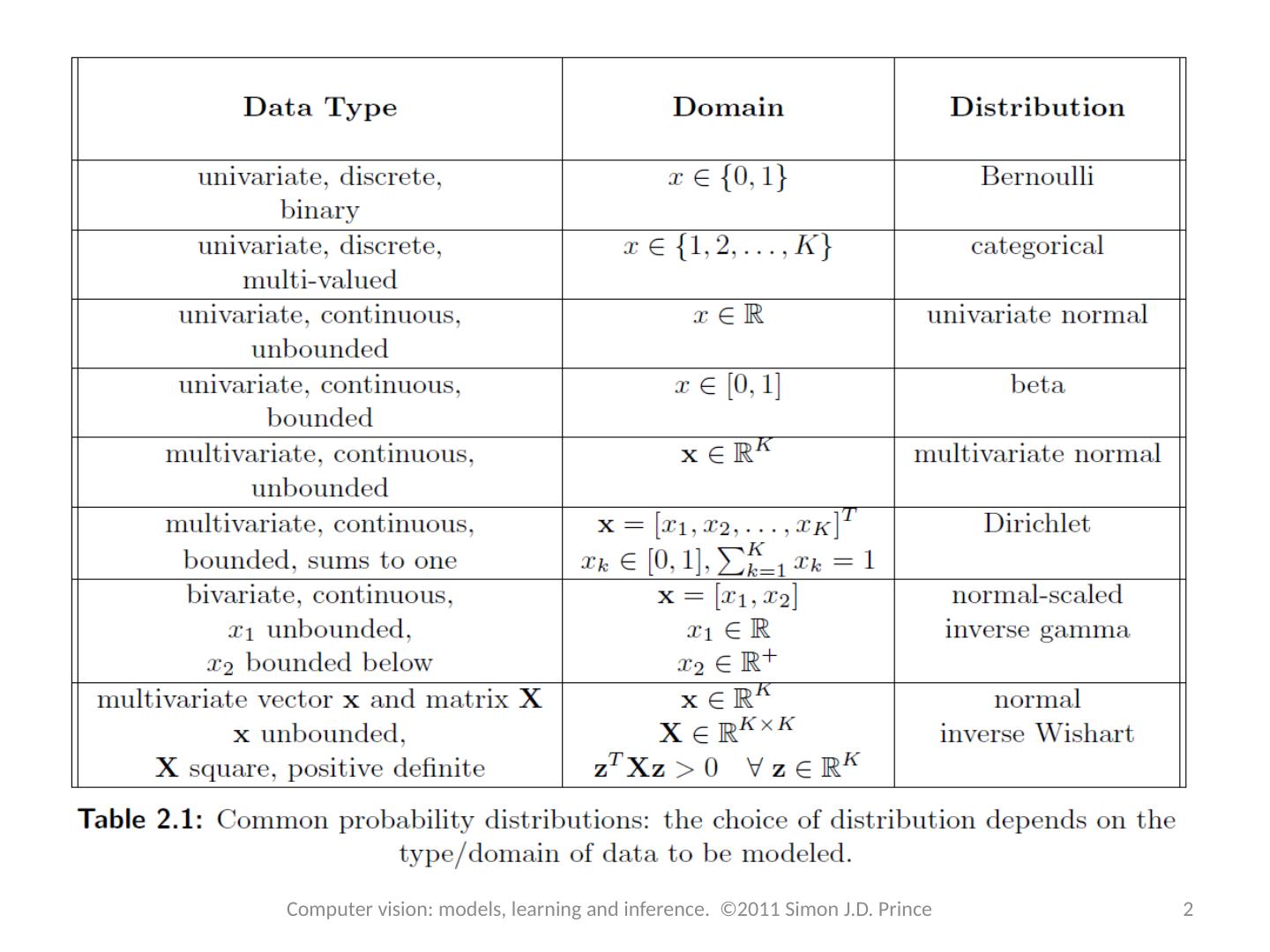
3 .Why model these complicated quantities? Because we need probability distributions over model parameters as well as over data and world state. Hence, some of the distributions describe the parameters of the others: 3 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

4 .Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Why model these complicated quantities? Because we need probability distributions over model parameters as well as over data and world state. Hence, some of the distributions describe the parameters of the others: Example: Models mean Models variance Parameters modelled by: 4

5 .Bernoulli Distribution or For short we write: Bernoulli distribution describes situation where only two possible outcomes y =0/ y =1 or failure/success Takes a single parameter 5 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

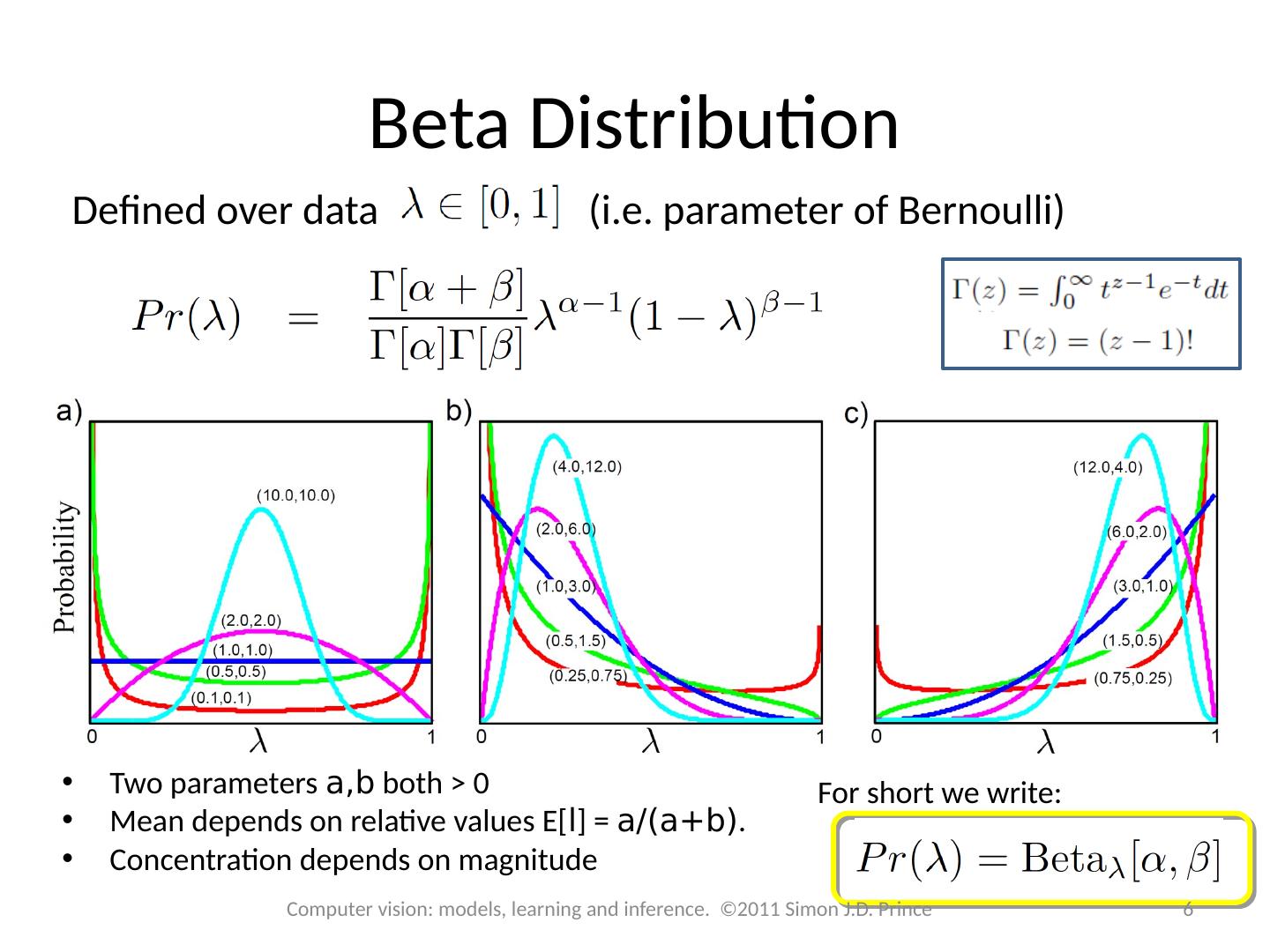
6 .Beta Distribution Defined over data (i.e. parameter of Bernoulli) Two parameters a,b both > 0 Mean depends on relative values E[ l ] = a/( a+b ) . Concentration depends on magnitude For short we write: 6 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

7 .Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Categorical Distribution or can think of data as vector with all elements zero except k th e.g. e 4 = [0,0,0,1,0] For short we write: Categorical distribution describes situation where K possible outcomes y=1… y=k . Takes K parameters where 7

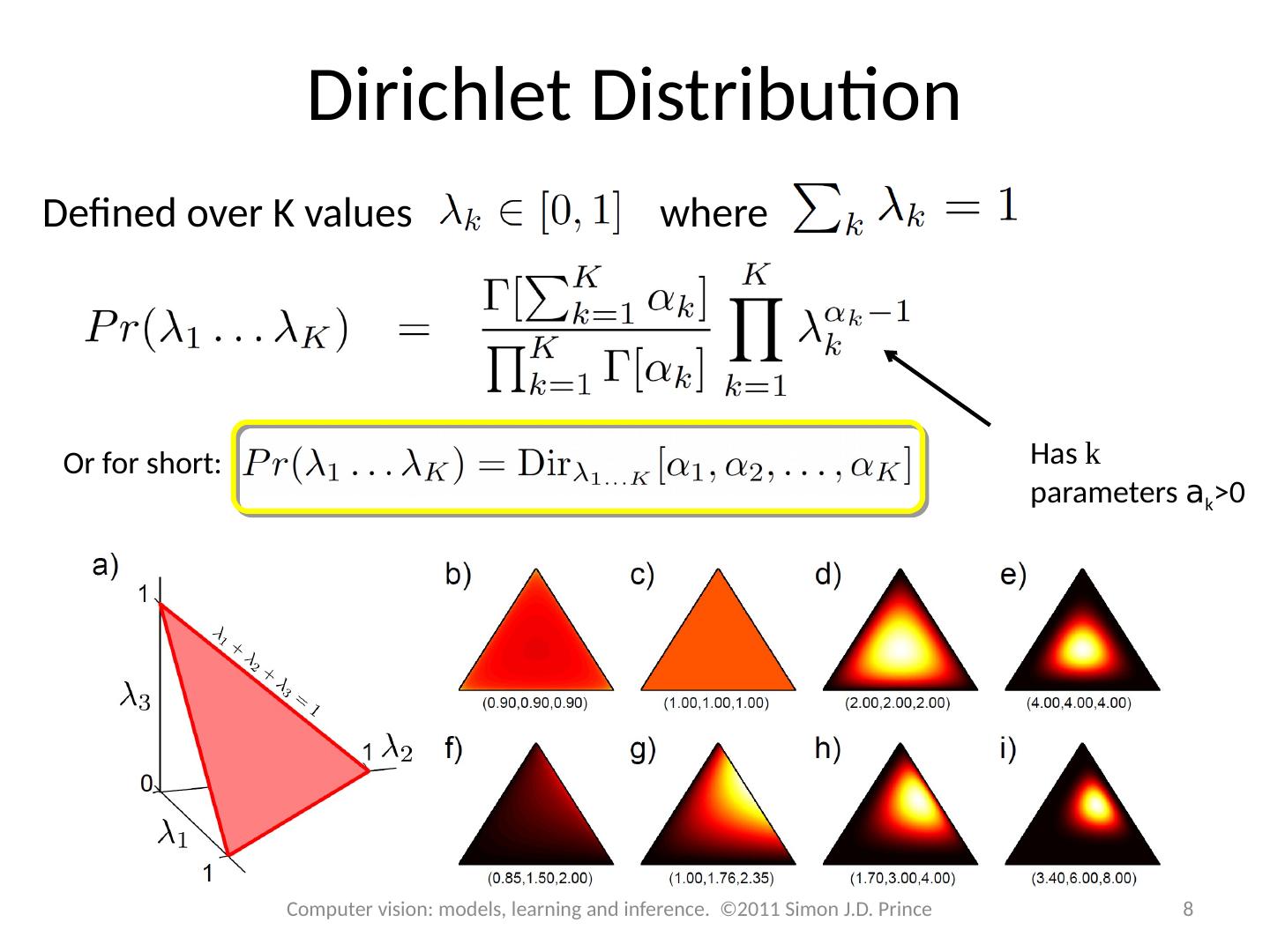
8 .Dirichlet Distribution Defined over K values where Or for short: Has k parameters a k >0 8 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

9 .Univariate Normal Distribution For short we write: Univariate normal distribution describes single continuous variable. Takes 2 parameters m and s 2 >0 9 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

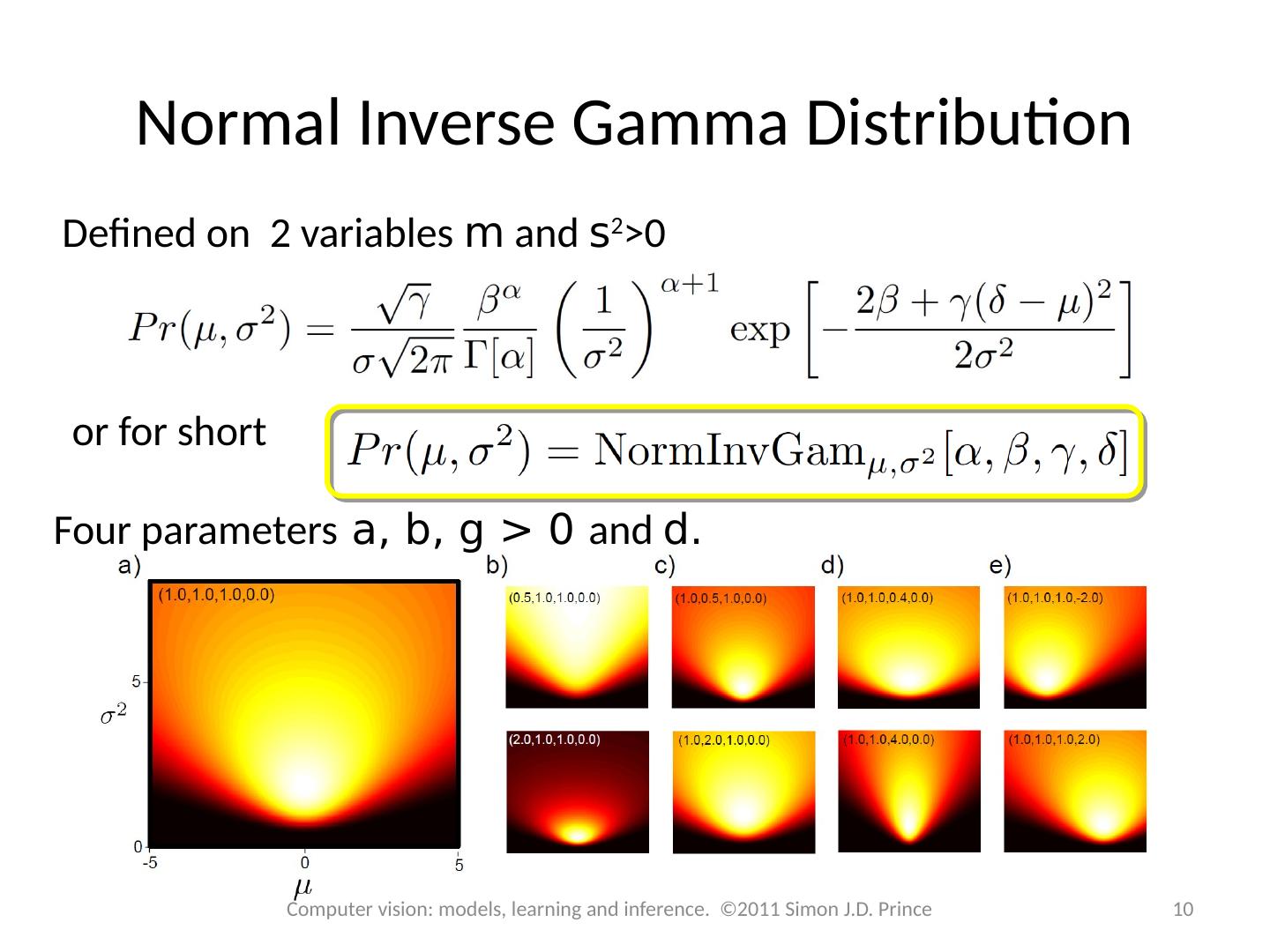
10 .Normal Inverse Gamma Distribution Defined on 2 variables m and s 2 >0 o r for short Four parameters a, b, g > 0 and d. 10 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

11 .Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Multivariate Normal Distribution For short we write: Multivariate normal distribution describes multiple continuous variables. Takes 2 parameters a vector containing mean position, m a symmetric “positive definite” covariance matrix S Positive definite: is positive for any real 11

12 .Types of covariance Covariance matrix has three forms, termed spherical , diagonal and full 12 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

13 .Normal Inverse Wishart Defined on two variables: a mean vector m and a symmetric positive definite matrix, S . or for short: Has four parameters a positive scalar, a a positive definite matrix Y a positive scalar, g a vector d 13 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

14 .Samples from Normal Inverse Wishart 14 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince (dispersion) ( ave . Covar ) ( disper of means) ( ave . of means)

15 .Conjugate Distributions The pairs of distributions discussed have a special relationship: they are conjugate distributions Beta is conjugate to Bernouilli Dirichlet is conjugate to categorical Normal inverse gamma is conjugate to univariate normal Normal inverse Wishart is conjugate to multivariate norma l 15 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

16 .Conjugate Distributions When we take product of distribution and it’s conjugate, the result has the same form as the conjugate. For example, consider the case where then a constant A new Beta distribution 16 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

17 .When we take product of distribution and it’s conjugate, the result has the same form as the conjugate. Example proof 17 17 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

18 .Bayes ’ Rule Terminology Posterior – what we know about y after seeing x Prior – what we know about y before seeing x Likelihood – propensity for observing a certain value of x given a certain value of y Evidence – a constant to ensure that the left hand side is a valid distribution 18 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

19 .Importance of the Conjugate Relation 1 Learning parameters: Choose prior that is conjugate to likelihood 2 . Implies that posterior must have same form as conjugate prior distribution 3. Posterior must be a distribution which implies that evidence must equal constant k from conjugate relation 19 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

20 .Importance of the Conjugate Relation 2 Marginalizing over parameters 1. Chosen so conjugate to other term 2 . Integral becomes easy --the product becomes a constant times a distribution Integral of constant times probability distribution = constant times integral of probability distribution = constant x 1 = constant 20 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince

21 .Conclusions 21 Computer vision: models, learning and inference. ©2011 Simon J.D. Prince Presented four distributions which model useful quantities Presented four other distributions which model the parameters of the first four They are paired in a special way – the second set is conjugate to the other In the following material we’ll see that this relationship is very useful