1

1 .压缩感知（ CS ） compressive sensing 报告人： 汪火根 2012.06.12 

2 .Contents 引例 

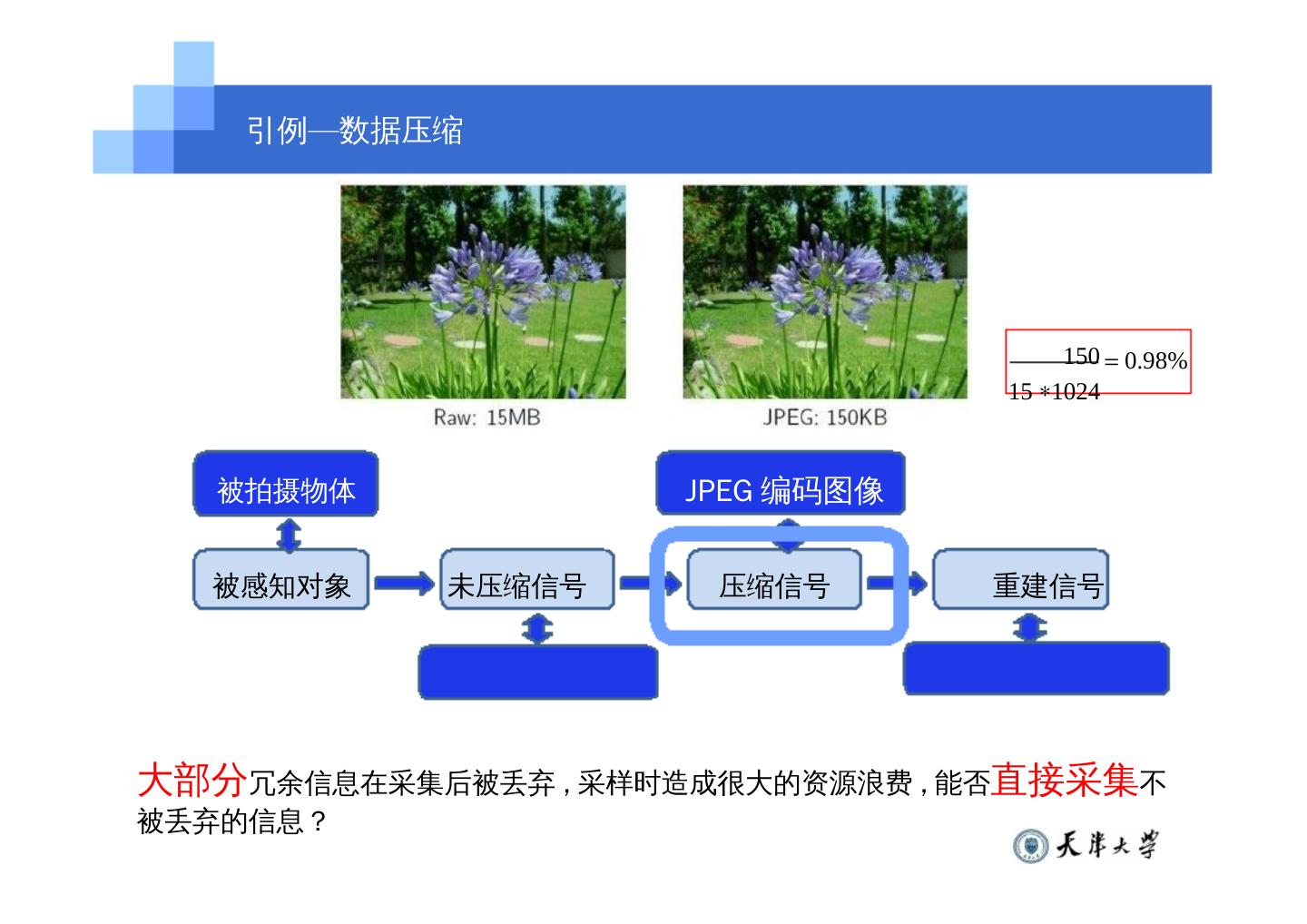
3 . 引例—数据压缩 150 0.98% 15 1024 被拍摄物体 JPEG 编码图像 被感知对象 未压缩信号 压缩信号 重建信号 通过显示器显示 RAW 图像 大部分冗余信息在采集后被丢弃 , 采样时造成很大的资源浪费 , 能否直接采集不 被丢弃的信息？ 

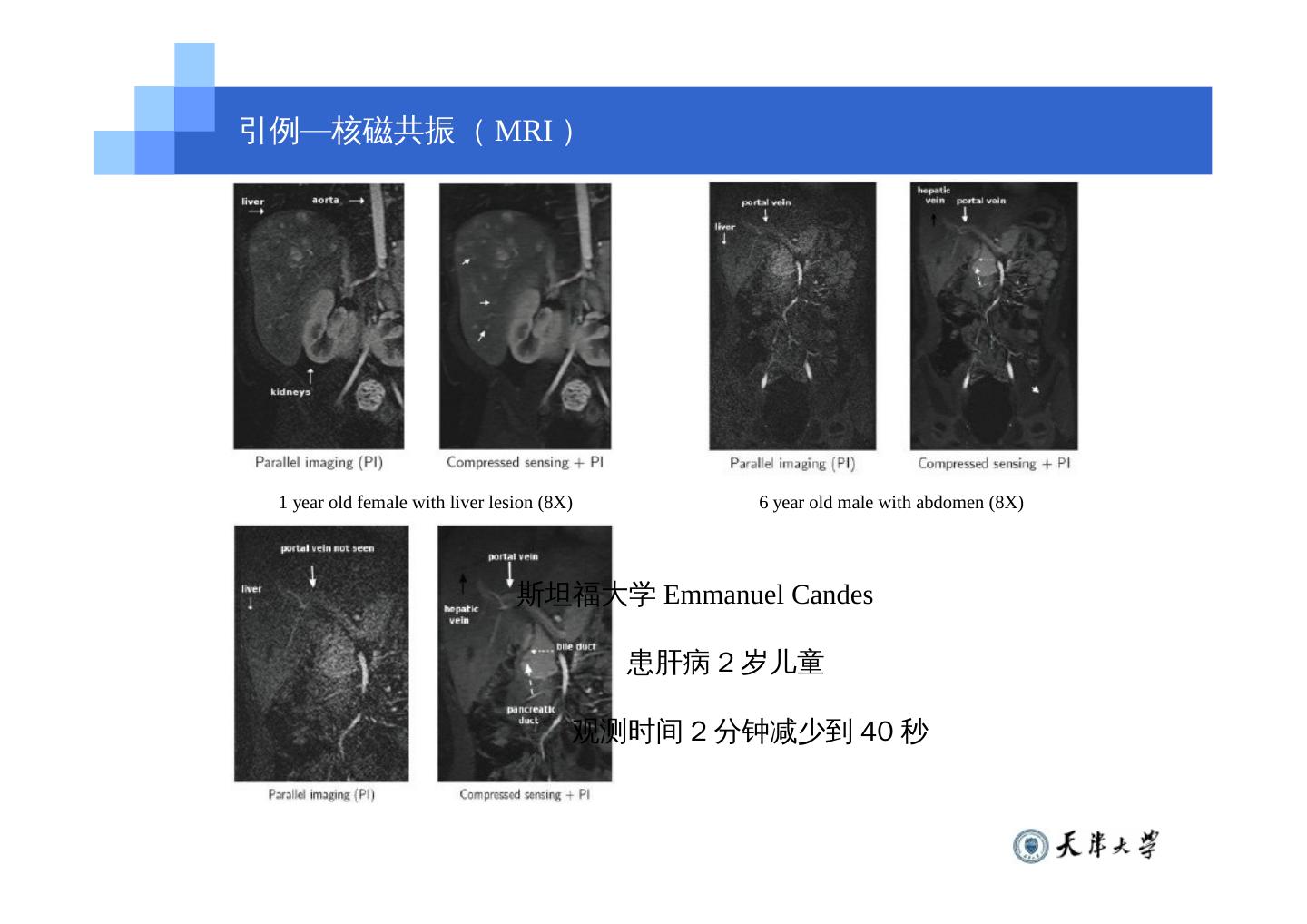
4 .引例—核磁共振（ MRI ） 1 year old female with liver lesion (8X) 6 year old male with abdomen (8X) 斯坦福大学 Emmanuel Candes 患肝病 2 岁儿童 观测时间 2 分钟减少到 40 秒 

5 . CS 的研究背景—数据压缩与解压缩的矛盾 数据压缩是从数据本身的特性出发，寻找并剔除数据中隐含的冗余度，从而达到 压缩的目的。这样的压缩有两个特点：第一、它是发生在数据已经被完整采集到之 后；第二、它本身需要复杂的算法来完成。相较而言，解码过程反而一般来说在计算 上比较简单，以音频压缩为例，压制一个 mp3 文件的计算量远大于播放（即解压缩） 数据采集及压缩设备 一个 mp3 文件的计算量。 数据解压缩设备 省电、 大型 廉价、 计算 计算 计算能 矛盾 高效 任务 任务 力较低 的计 复杂 简单 的便携 算机 设备 

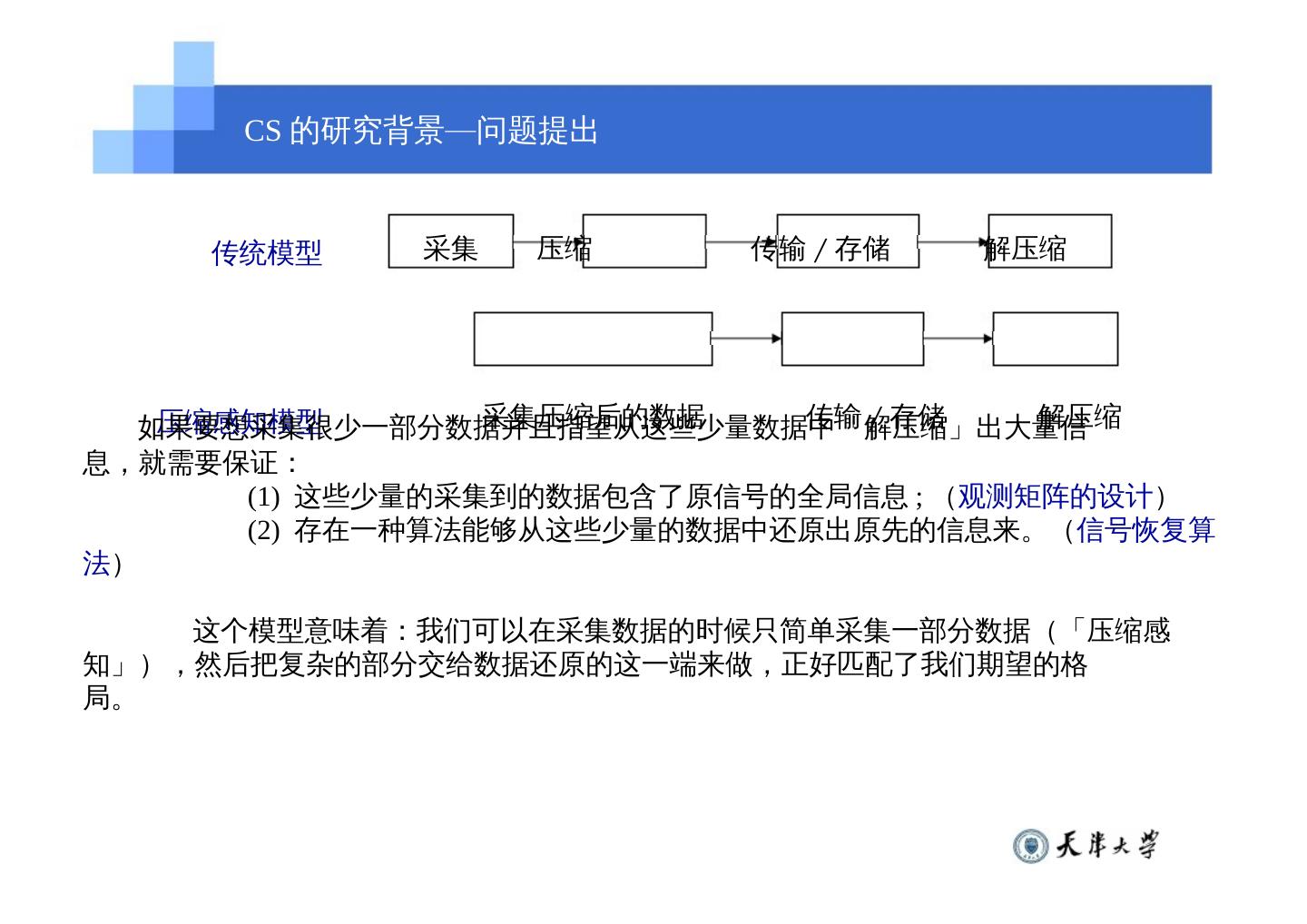
6 . CS 的研究背景—问题提出 传统模型 采集 压缩 传输 / 存储 解压缩 压缩感知模型 采集压缩后的数据 传输 / 存储 如果要想采集很少一部分数据并且指望从这些少量数据中「解压缩」出大量信 解压缩 息，就需要保证： (1) 这些少量的采集到的数据包含了原信号的全局信息 ; （观测矩阵的设计） (2) 存在一种算法能够从这些少量的数据中还原出原先的信息来。（信号恢复算 法） 这个模型意味着：我们可以在采集数据的时候只简单采集一部分数据（「压缩感 知」），然后把复杂的部分交给数据还原的这一端来做，正好匹配了我们期望的格 局。 

7 . CS 的研究背景—问题提出 2006 年，由 D. Donoho( 美国科学院院士 ) 、 E. Candes(Ridgelet, Curvelet 创始人 ) 及华裔科学家 T. Tao(2006 年菲尔兹奖获得者， 2008 年被评为世界上最聪明的科学家 ) 等 人提出了一种新的信息获取指导理论，即，压缩感知。该理论指出：对可压缩的信号可 通过远低于 Nyquist 标准的方式进行采样数据，仍能够精确地恢复出原始信号。该理论 一经提出，就在信息论、信号 / 图像处理、医疗成像、模式识别、地质勘探、光学 / 遥感 成像、无线通信，雷达探测，生物传感，集成电路分析，图像超分辨率重建等领域受到 高度关注，并被美国科技评论评为 2007 年度十大科技进展。 D. Donoho 因此还获得了 2008 年 IEEE 学会最佳论文奖。 《 Robust Uncertainty Principles: Exact Signal Reconstruction From Highly Incomplete Frequency Information 》 IEEE Transactions on Information Theory, Feb. 2006 《 Quantitative Robust Uncertainty Principles and Optimally Sparse Decompositions 》 Foundations of Computational Mathematics, Apr. 2006 《 Near Optimal Signal Recovery From Random Projections: Universal Encoding Strategies? 》 IEEE Transactions on Information Theory, Dec. 2006 Dave Donoho Emmanuel Candes Terence Tao 

8 . CS 的研究内容—压缩感知定义 压缩感知是一种新的在对稀疏或者可压缩信号采样的同时实现压缩目的的 理论框架。它是通过一组特定波形去感知信号，即将信号投影到给定波形上面， 获得到一组压缩数据；最后利用最优化的方法实现对压缩数据解压，估计出原始 信号的重要信息。 压缩感知的核心思想是压缩和采样合并进行，并且测量值远小于传统采 样方法的数据量，突破了香农采样定理的瓶颈，使高分辨率的信号采集成为可 能。毫无疑问是一种有着极大理论和应用前景的想法。它是传统信息论的一个 延伸，但是又超越了传统的压缩理论，成为了一门崭新的子分支。 其他名称：压缩采样；压缩传感 Compressed sensing; Compressive sampling; Compressive sensing; Compressed sampling 

9 . CS 的研究内容—压缩感知的过程 压缩感知的过程 1) 首先利用变换空间描述信号（稀疏变换）； 2) 通过特定波形的“感知”直接采集得到少数精挑细选的线性观测数 据 , 将信号的采样转变成信息的采样； 3) 通过解一个优化问题（因为求解的是一个欠定的方程组）就可以 从压缩观测的数据中恢复原始信号。 

10 .CS 的研究内容—压缩感知数学模型 

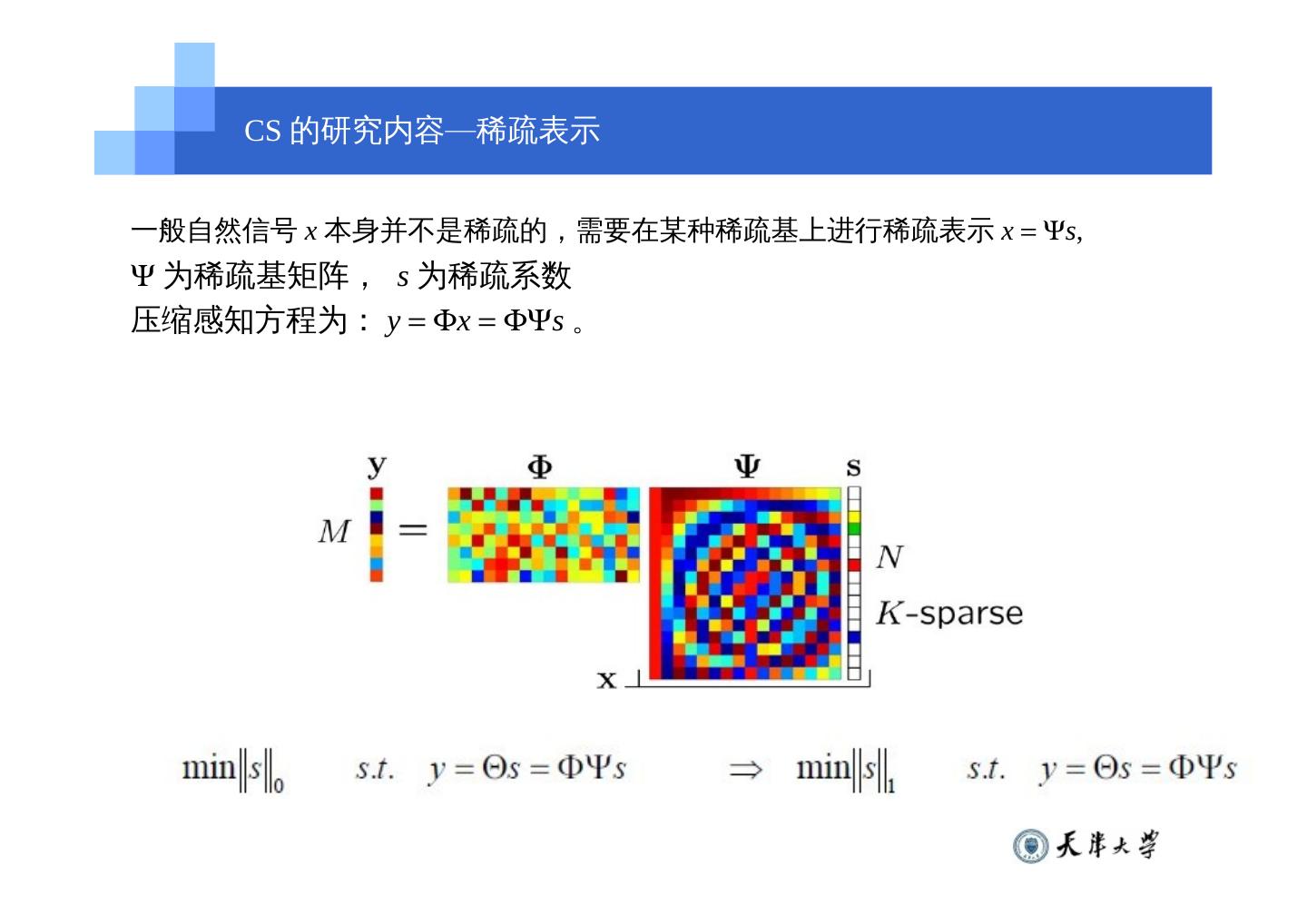
11 . CS 的研究内容—稀疏表示 一般自然信号 x 本身并不是稀疏的，需要在某种稀疏基上进行稀疏表示 x s,  为稀疏基矩阵， s 为稀疏系数 压缩感知方程为： y x s 。 

12 . CS 的研究内容—稀疏表示 信号的稀疏表示就是将信号投影到正交变换基时 , 绝大部分变换系数的绝对值很 小 , 所得到的变换向量是稀疏或者近似稀疏的 , 可以将其看作原始信号的一种简洁表 达 , 这是压缩感知的先验条件。变换基可以根据信号的本身特点灵活选取，常用的有 离散余弦变换（ DCT ）、傅里叶变换（ FFT ）、离散小波变换（ DWT ）， Gabor 变换等。 Peyre 把变换基是正交基的条件扩展到了由多个正交基构成的正交基字典。即在 某个正交基字典里，自适应地寻找可以逼近某一种信号特征的最优正交基，根据不同 的信号寻找最适合信号特性的一个正交基，对信号进行变换得到最稀疏的信号表示。 最近几年，对稀疏表示研究的另一个热点是信号在冗余字典下的稀疏分解。 这 是一种全新的信号表示理论：用超完备的冗余函数库取代基函数，称之为冗余字典， 字典中的元素被称为原子。目前信号在冗余字典下的稀疏表示的研究集中在两个方面： 一是如何构造一个适合某一类信号的冗余字典，二是如何设计快速有效的稀疏分解算 法。目前常用的稀疏分解算法大致可分为匹配追踪（ Matching Pursuit ）和基追踪 （ Basis Pursuit ）两大类。 

13 . CS 的研究内容—感知矩阵设计 压缩感知理论中，通过变换得到信号的稀疏系数后 , 需要设计压缩采样系统的观 测部分，它围绕观测矩阵 Φ 展开。观测器的设计目的是如何采样得到 M 个观测值，并 保证从中能重构出长度为 N 的信号 x 或者稀疏基基 Ψ 下等价的稀疏系数向量。 CandeS 和 Tao 等证明 : 独立同分布的高斯随机测量矩阵可以成为普适的压缩感知测 量矩阵。 2007 年 Candes 等研究者建立了著名的约束等距性（ RIP ）理论，即要想使信 号完全重构，必须保证观测矩阵不会把两个不同的 K 项稀疏信号映射到同一个采样 集合中，这就要求从观测矩阵中抽取的每 M 个列向量构成的矩阵是非奇异的。 Donoho 给出压缩感知概念的同时定性和定量的给出测量矩阵要满足三个特征：① 由测量矩阵的列向量组成的子矩阵的最小奇异值必须大于一定的常数；②测量矩阵 的列向量体现某种类似噪声的独立随机性；③满足稀疏度的解是满足 1 范数最小的向 量。 

14 . CS 的研究内容—重构算法 压缩感知的重构算法主要分为三大类： 1) 凸优化算法，它是把非凸问题转换为凸问题通过线性规划找到信号的逼近，此 类算法主要包括梯度投影法、基追踪法 (BP) 、内点法、最小角度回归法等。 2) 贪婪算法，它是通过选择合适的原子并经过每次迭代选择的局部最优解来逐步 逼近原始信号。此类算法主要包括匹配跟踪算法 (MP) 、正交匹配追踪算法 (OMP) 、分段 正交匹配追踪（ StOMP ） , 正则化正交匹配追踪 (ROMP), 子空间追踪（ SP ） , 压缩采样追 踪（ CoSaOMP ）算法等。 3) 组合算法，它要求信号的采样支持通过分组测试快速重建，此类算法主要包括 傅里叶采样，链式追踪和 HHS 追踪等。 此外，迭代阈值法也得到了广泛的应用，此类算法也较易实现，计算量适中，在 贪婪算法和凸优化算法中都有应用。但是，迭代阈值法对于迭代初值和阈值的选取均 较敏感，且不能保证求出的解是稀疏的。 就目前主流的两种重建算法而言，凸优化算法算法比贪婪算法所求的解更加精确 , 基于 1 范数最小的重建算法计算量巨大，对于大规模信号无法应用；贪婪算法虽然重建 速度快，但是在信号重建质量上还有待提高。 

15 . CS 的研究现状 国外：在美国、英国、德国、法国、瑞士、以色列等许多国家的知名大学 ( 例如，麻省 理工学院 , 斯坦福大学，普林斯顿大学，莱斯大学，杜克大学，慕尼黑工业大学，爱丁 堡大学，等等 ) 成立专门课题组对 CS 进行研究； 2008 年， Intel ，贝尔实验室， Google 等 知名公司也开始组织研究 CS ； 2009 年，美国空军实验室和杜克大学联合召开 CS 研讨会， 与会报告的有小波专家 R. Coifman 教授，信号处理专家 James McClellan 教授，微波遥 感专家 Jian Li 教授，理论数学专家 R.DeVore 教授 , 美国国防先期研究计划署 (DARPA) 和 美国国家地理空间情报局 (NGA) 等政府部门成员。 2011 年 7 月 26—28 日在杜克大学召开第 二次以压缩感知和高维数据分析为主题的研讨会。 国内：一些高校和科研机构也开始追踪 CS 的研究。如清华大学（戴琼海），西安电子科 技大学（石光明，焦李成），中科院电子所，西安交通大学（徐宗本），西南交通大学 等。国家自然科学基金委也自 2009 年资助了多项压缩感知方法的研究，涉及无线电，雷 达成像，信号稀疏表示，多媒体编码，人脸识别等领域。 综述性论文 15 篇以上 

16 . CS 的研究现状 目前 CS 理论的研究尚属于起步阶段，但已表现出了强大的生命力，并已发展了分布 CS 理论 (Baron 等提出 ) ， 1-BIT CS 理论 (Baraniuk 等提出 ) ， Bayesian CS 理论 (Carin 等提 出 ) ，无限维 CS 理论 (Elad 等提出 ) ，变形 CS 理论 (Meyer 等提出 ) ，谱 CS 理论（ Duarte 等提 出），边缘 CS 理论（ Guo 等提出）， Kronecker CS 理论（ Duarte 等提出），块 CS 理论 （ Gan 等提出）等等，已成为数学领域和工程应用领域的一大研究热点。它们不仅为许多 应用科学如统计学、信息论、编码理论、计算机科学等带来了新的启发 , 而且在许多工程 领域如低成本数码相机和音频采集设备、节电型图像采集设备、高分辨率地理资源观测、 分布式传感器网络、超宽带信号处理等都具有重要的实践意义 . 尤其是在成像方面如地震 勘探成像和核磁共振成像中 , 基于 CS 理论的新型传感器已经设计成功 , 将对昂贵的成像器 件的设计产生重要的影响。在宽带无线频率信号分析中 , 基于 CS 理论的欠 Nyquist 采样设 备的出现 , 将摆脱目前 A/D 转换器技术的限制困扰。 自从 2006 年 CS 的提出，在 IEEE 的信号处理汇刊，信号处理快报汇刊，信号处理杂 志，信息论汇刊等国际知名期刊上开始涌现出上百篇关于 CS 理论与应用方面的文献。 2010 年，《 IEEE Journal of Selected Topics in Signal Processing 》专门出版了一 期关于 CS 的专刊，促进了 CS 在各个领域应用成果的交流。 2011 年 4 月，第一本关于 CS 的专 著《 Compressed Sensing: Theory and Applications 》出版，不仅系统的介绍了 CS 的概 念，而且汇集了世界各国学者在 CS 理论和应用上的观点和成功范例。 Compressive Sensing Resources http://dsp.rice.edu/cs 

17 . 研究工作 将 CS 理论应用于多描述编码。利用压缩感知理论的直接压缩采样特性，提出一种新 的 CS-MDC 编码方法。该方法不仅可以极大地提高多描述编码的抗丢包能力，而且使得 图 像 / 信号的采样和压缩同时以非常低的速率进行，使传感器的采样率和计算成本大大 降 40   低。而传统多描述编码的采样过程建立在奈奎斯特采样意义上，编码端处理成本高。 SPIHT Coding 35 CS Coding 下图是 CS 编码和基于 SPIHT( 多级树几何分裂排序 ) 的多描述编码方法的实验对比， 30 码率为 1.0 25 ，从仿真结果图可以看出， CS 编码方法在抗丢包率性能方面优于 SPIHT PSNR 编码方法。20 15 10 5   5% 15% 25% 35% 45% 55% 65% 75% 85% 丢包率 

18 .www.themegallery.com