08_Artificial Neural networks

1 .Ch. 8: Artificial Neural networks Introduction to Back Propagation Neural Networks BPNN By KH Wong Neural Networks Ch9. , ver. 8d2 1

2 .Introduction Neural Network research is are very hot A high performance Classifier (multi-class) Successful in handwritten optical character OCR recognition, speech recognition, image noise removal etc. Easy to implement Slow in learning Fast in classification Neural Networks Ch9. , ver. 8d2 2 Example and dataset: http ://yann.lecun.com/exdb/mnist /

3 .Motivation Biological findings inspire the development of Neural Net Input  weights Logic function output Biological relation Input Dendrites Output Human computes using a net Neural Networks Ch9. , ver. 8d2 3 X=inputs W=weights Neuron(Logic function) Output https://www.ninds.nih.gov/Disorders/Patient-Caregiver-Education/Life-and-Death-Neuron

4 .Applications Microsoft: XiaoIce. AI http://image-net.org/challenges/LSVRC/2015/ 200 categories: accordion, airplane ,ant ,antelope ….dishwasher ,dog ,domestic cat ,dragonfly ,drum ,dumbbell , etc. Tensor flow Neural Networks Ch9. , ver. 8d2 4 ILSVRC 2015 Number of object classes 200 Training Num images 456567 Num objects 478807 Validation Num images 20121 Num objects 55502 Testing Num images 40152 Num objects ---

5 .Different types of artificial neural networks Autoencoder DNN Deep neural network   & Deep learning MLP Multilayer perceptron RNN (Recurrent Neural Networks), LSTM (Long Short-term memory) RBM Restricted Boltzmann machine SOM (Self-organizing map) Convolutional neural network CNN From https://en.wikipedia.org/wiki/Artificial_neural_network The method discussed in this power point can be applied to many of the above nets. Neural Networks Ch9. , ver. 8d2 5

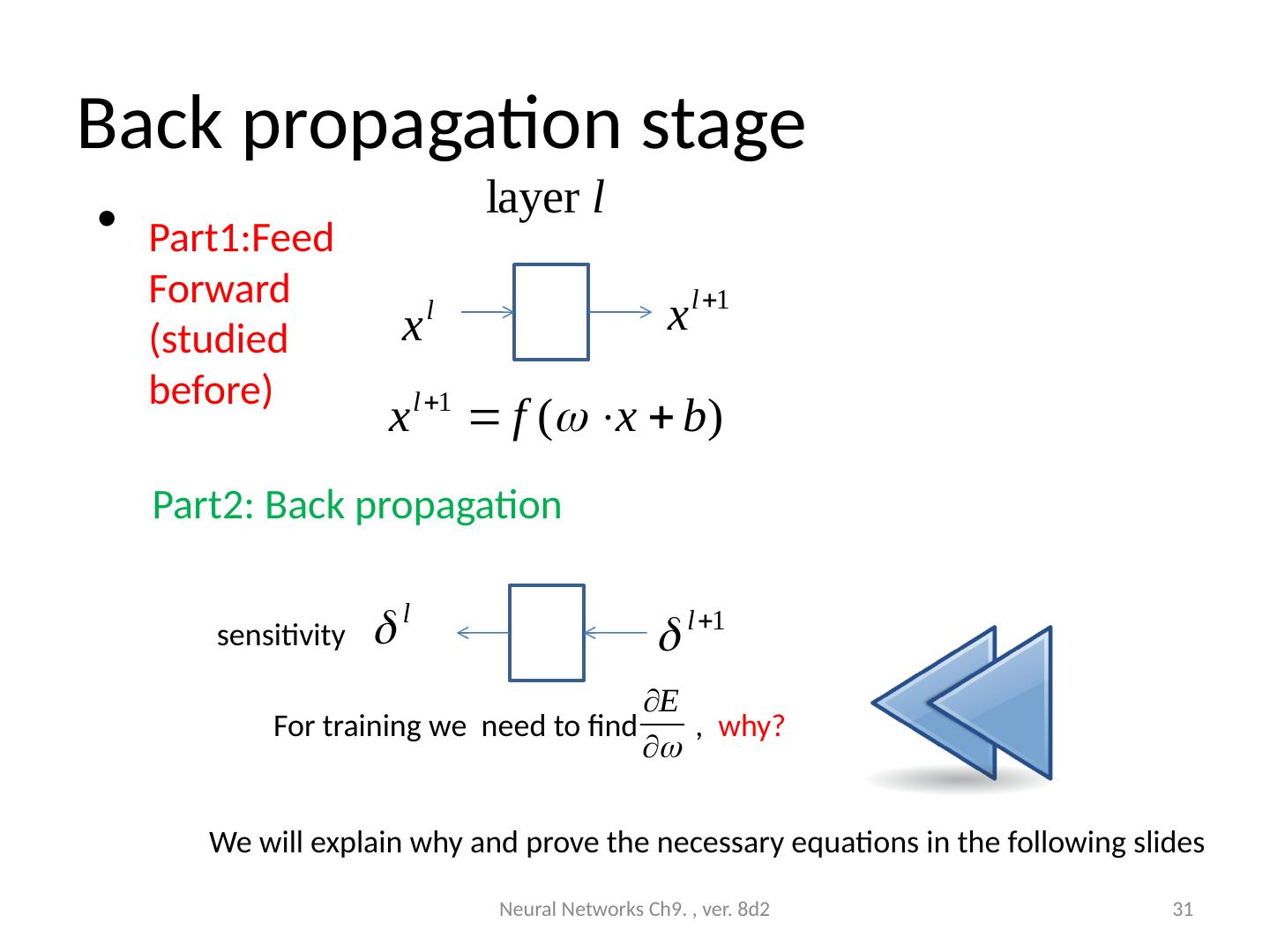
6 .Theory of Back Propagation Neural Net (BPNN) Use many samples to train the weights (W) & Biases (b), so it can be used to classify an unknown input into different classes Will explain How to use it after training: forward pass (classify /or the recognition of the input ) How to train it: how to train the weights and biases (using forward and backward passes) Neural Networks Ch9. , ver. 8d2 6

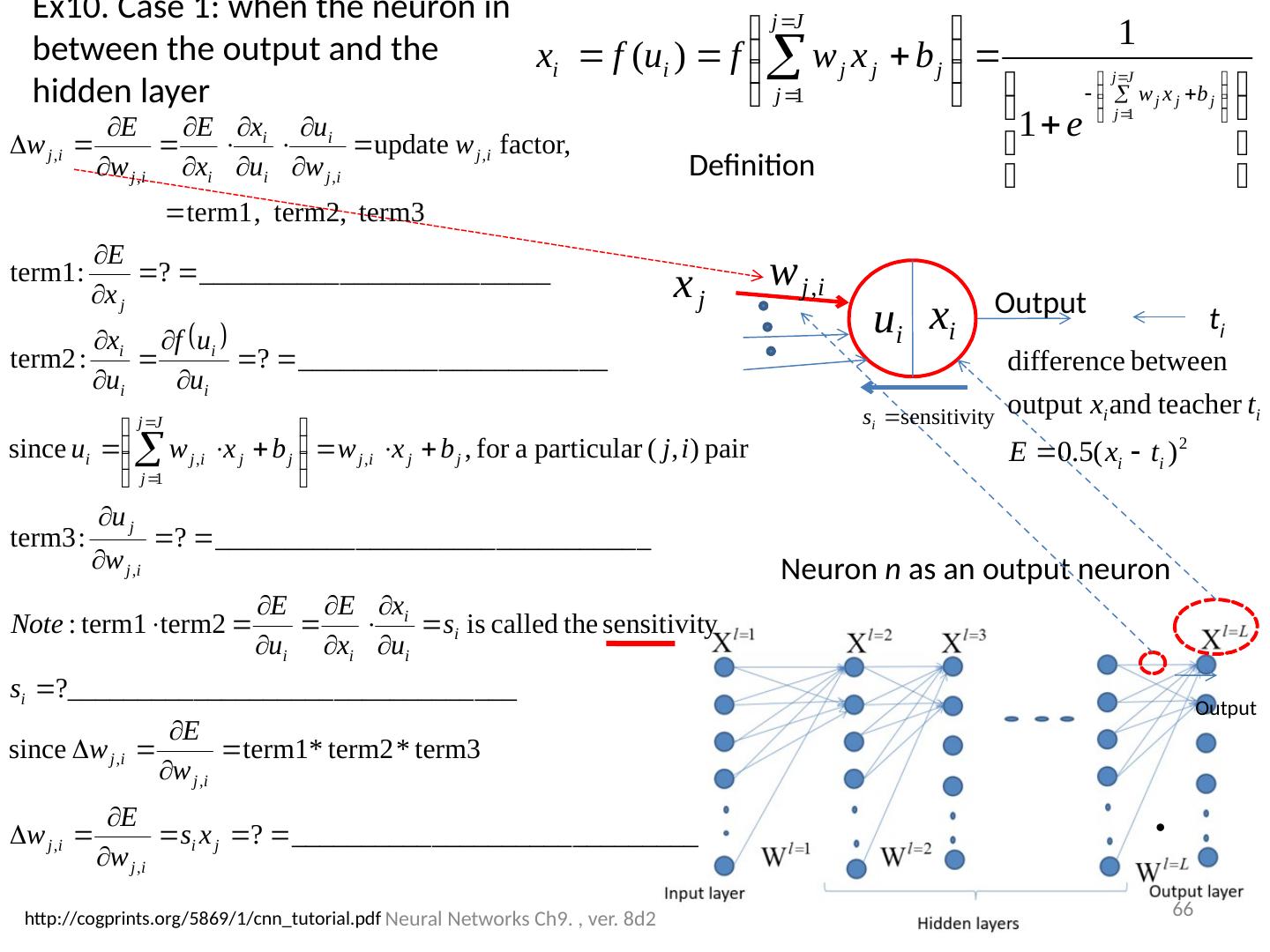
7 .Back propagation is an essential step in many artificial network designs Used to train an artificial neural network For each training example x i , a supervised (teacher) output t i is given. For each i th training sample x: x i Feed forward propagation: feed x i to the neural net, obtain output y i . Error e i  | t i -y i | 2 Back propagation: feed e i back to net from the output side and adjust weight w (by finding ∆w) to minimize e. Repeat 1) and 2) for all samples until E is 0 or very small. Neural Networks Ch9. , ver. 8d2 7

8 .Example :Optical character recognition OCR Training: Train the system first by presenting a lot of samples with known classes to the network Recognition: When an image is input to the system, it will tell what character it is Neural Networks Ch9. , ver. 8d2 8 Neural Net Output3=‘1’, other outputs=‘0’ Neural Net Training up the network: weights (W) and bias (b)

9 .Overview of this document Back Propagation Neural Networks (BPNN) Part 1: Feed forward processing (classification or Recognition) Part 2: Back propagation (Training the network), also include forward processing, backward processing and update weights Appendix: A MATLAB example is explained %source : http://www.mathworks.com/matlabcentral/fileexchange/19997-neural-network-for-pattern-recognition-tutorial Neural Networks Ch9. , ver. 8d2 9

10 .Part 1 (classification in action /or the Recognition process) Forward pass of Back Propagation Neural Net (BPNN) Assume weights (W) and bias (b) are found by training already (to be discussed in part2) Neural Networks Ch9. , ver. 8d2 10

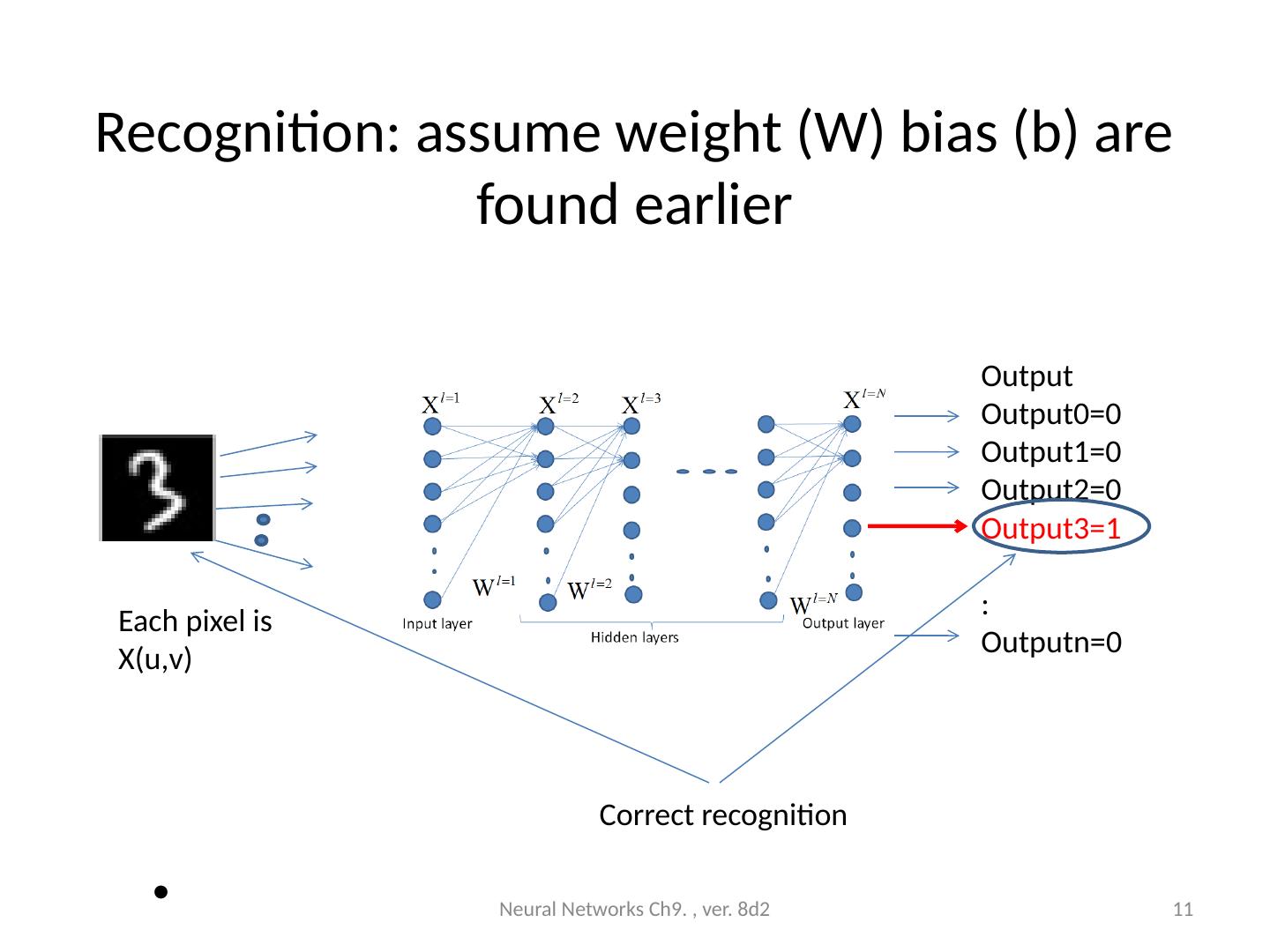
11 .Recognition: assume weight (W) bias (b) are found earlier Neural Networks Ch9. , ver. 8d2 11 Output Output0=0 Output1=0 Output2=0 Output3=1 : Outputn=0 Each pixel is X(u,v) Correct recognition

12 .A neural network Neural Networks Ch9. , ver. 8d2 12 Output layer Input layer Hidden layers

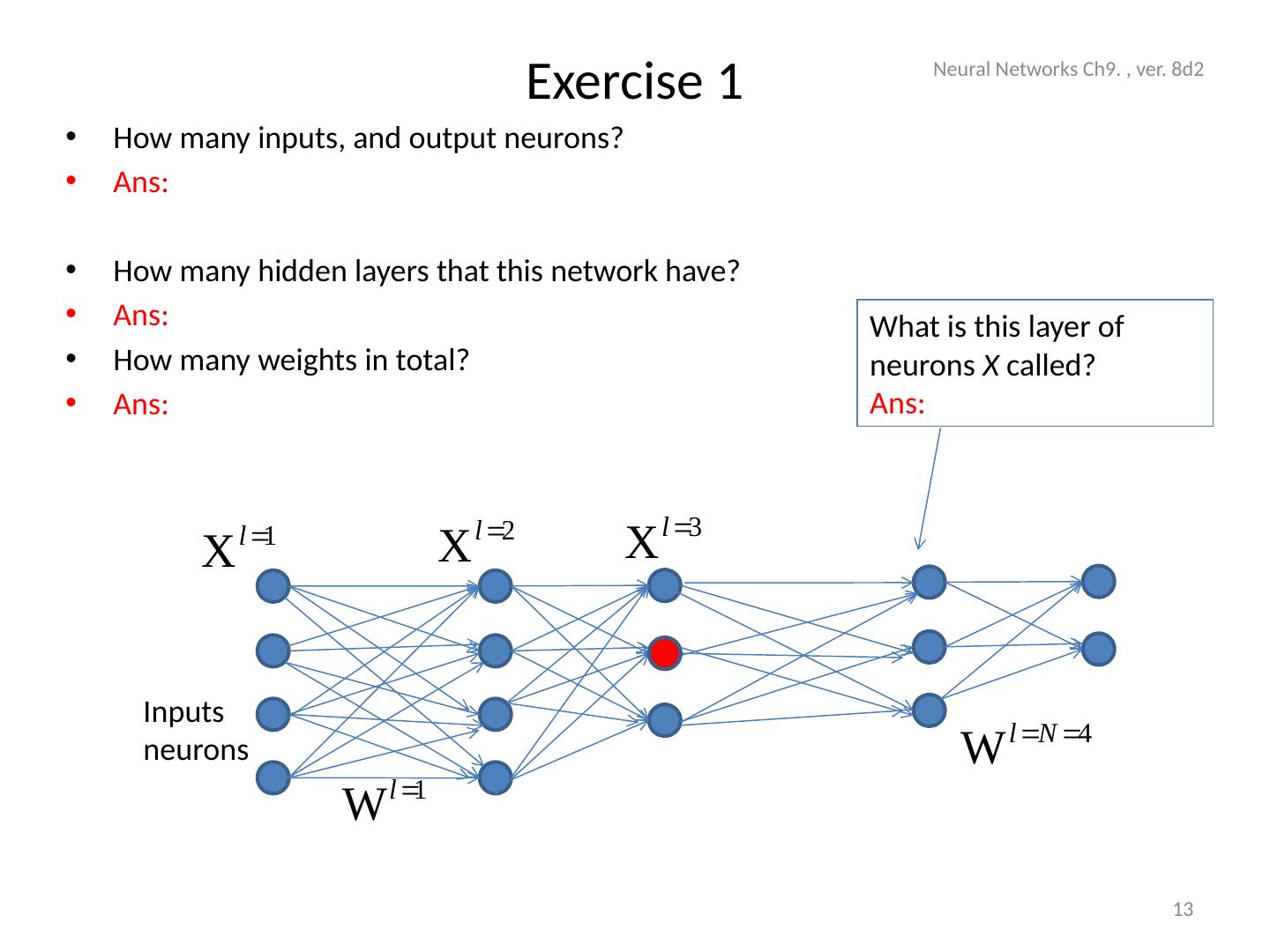
13 .Exercise 1 How many inputs, and output neurons? Ans : How many hidden layers that this network have? Ans : How many weights in total? Ans : Neural Networks Ch9. , ver. 8d2 13 Inputs neurons What is this layer of neurons X called? Ans :

14 .ANSWER: Exercise 1 How many inputs and output neurons? Ans : 4 input and 2 output neurons How many hidden layers that this network have? Ans : 3 How many weights in total? Ans : First hidden layer has 4x4, second layer has 3x4, third hidden layer has 3x3, fourth hidden layer to output layer has 2x3 weights. total=16+12+9+6=43 Neural Networks Ch9. , ver. 8d2 14 Inputs neurons What is this layer of neurons X called? Ans:

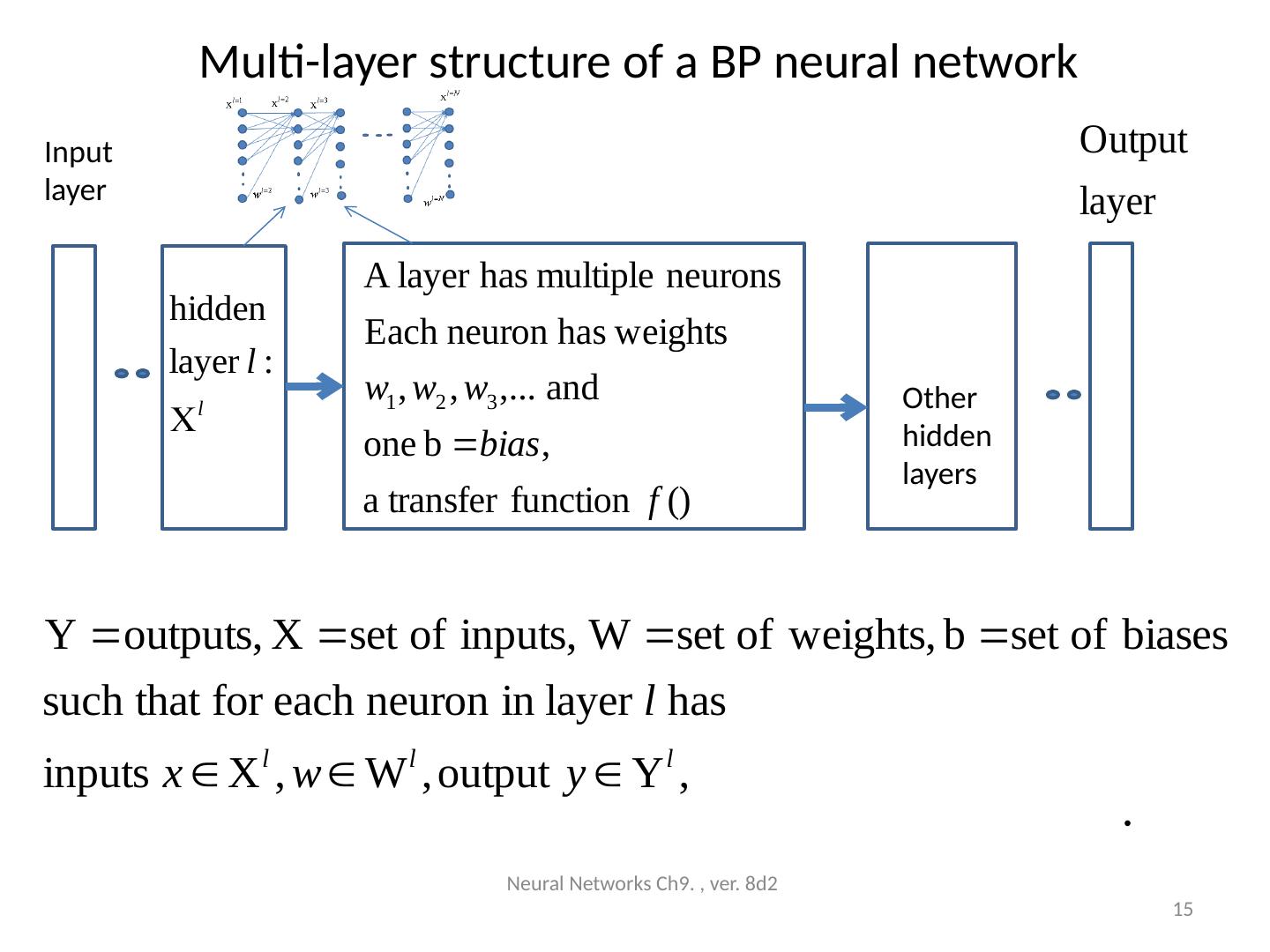
15 .Multi-layer structure of a BP neural network Neural Networks Ch9. , ver. 8d2 15 Input layer Other hidden layers

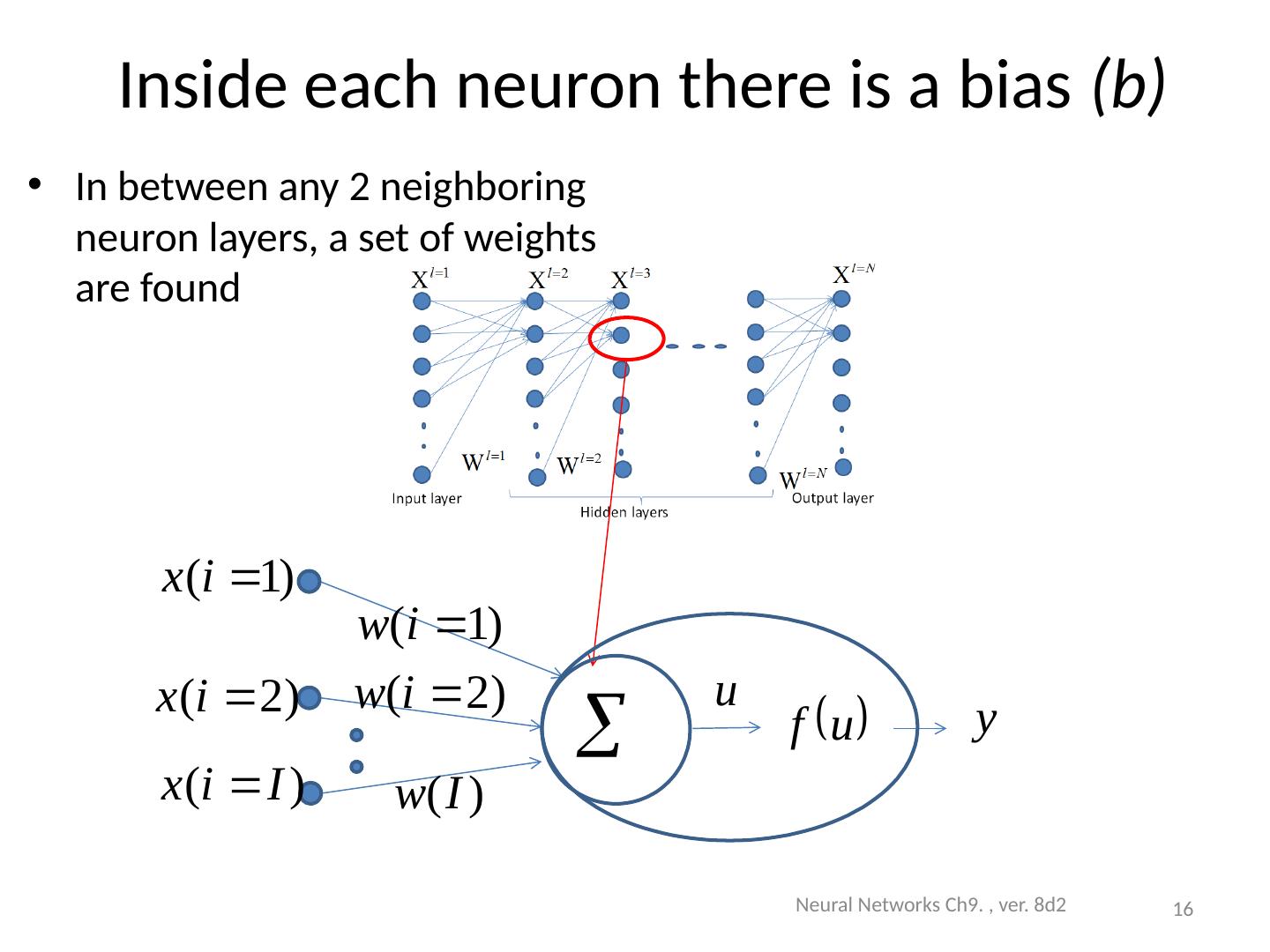
16 .Inside each neuron there is a bias (b) In between any 2 neighboring neuron layers, a set of weights are found Neural Networks Ch9. , ver. 8d2 16

17 .Inside each neuron x =input, y =output Neural Networks Ch9. , ver. 8d2 17

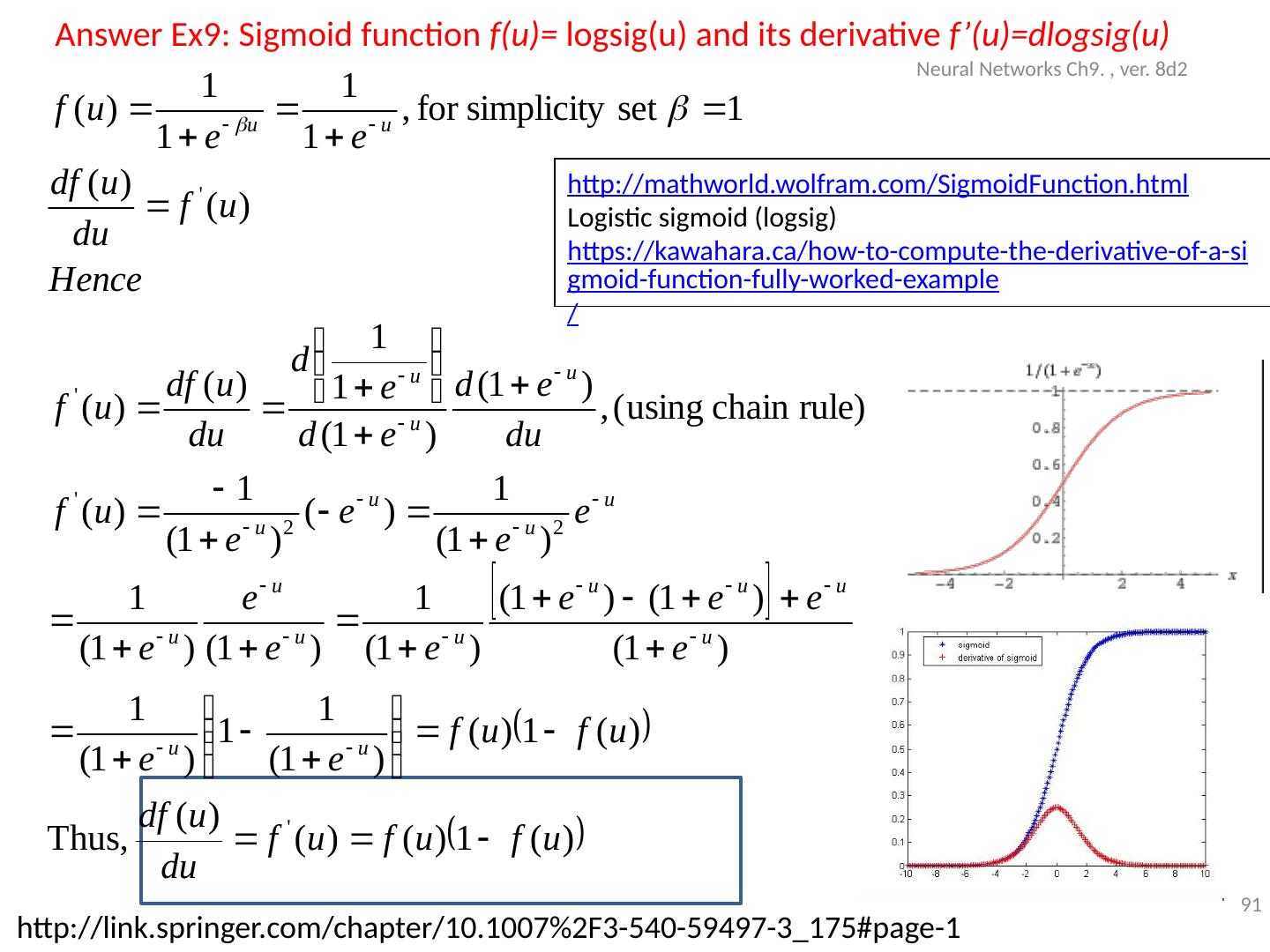
18 .Sigmoid function f(u)= logsig (u) and its derivative f’(u)= dlogsig (u) Neural Networks Ch9. , ver. 8d2 18 http:// link.springer.com/chapter/10.1007%2F3-540-59497-3_175#page-1 , https ://imiloainf.wordpress.com/2013/11/06/rectifier-nonlinearities / http:// mathworld.wolfram.com/SigmoidFunction.html Logistic sigmoid ( logsig ) https://kawahara.ca/how-to-compute-the-derivative-of-a-sigmoid-function-fully-worked-example /

19 .Back Propagation Neural Net (BPNN) Forward pass Forward pass is to find the output when an input is given. For example: Assume we have used N=60,000 images ( MNIST database ) to train a network to recognize c=10 numerals. When an unknown image is given to the input, the output neuron corresponds to the correct answer will give the highest output level. Neural Networks Ch9. , ver. 8d2 19 10 output neurons for 0,1,2,..,9 Input image 0 0 0 1 0 0

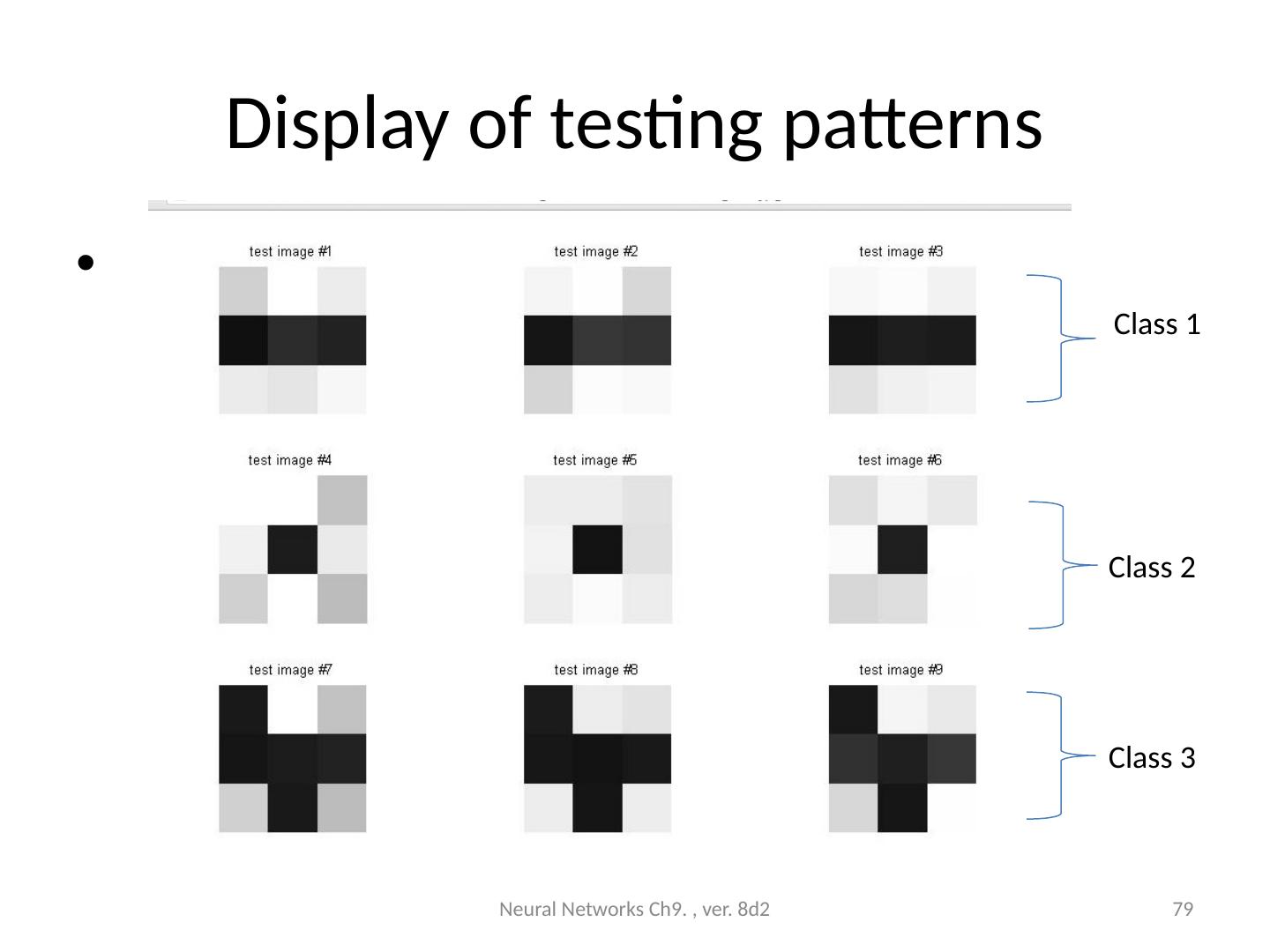
20 .Our simple demo program Training pattern 3 classes (in 3 rows) Each class has 3 training samples (items in each row) After training , an input (assume it is test image #2) is presented to the network, the network should tell you it is class 2, etc. Neural Networks Ch9. , ver. 8d2 20 class1 class2 class3 Result :image (class 2 ) Unknown input

21 .Numerical Example : Architecture of our example (see code in appendix) Neural Networks Ch9. , ver. 8d2 21 Input Layer 9x1 pixels output Layer 3x1

22 .The input x P2=[50 30 25 215 225 231 31 22 34; ... %class1: 1st training sample. Gray level 0->255 Neural Networks Ch9. , ver. 8d2 22 P1=50 P2=30 P3=25 P4=215 P5=225 P6=235 P7=31 P8=22 P9=34 9 neurons In input layer 3 neurons In output layer 5 neurons In hidden layer

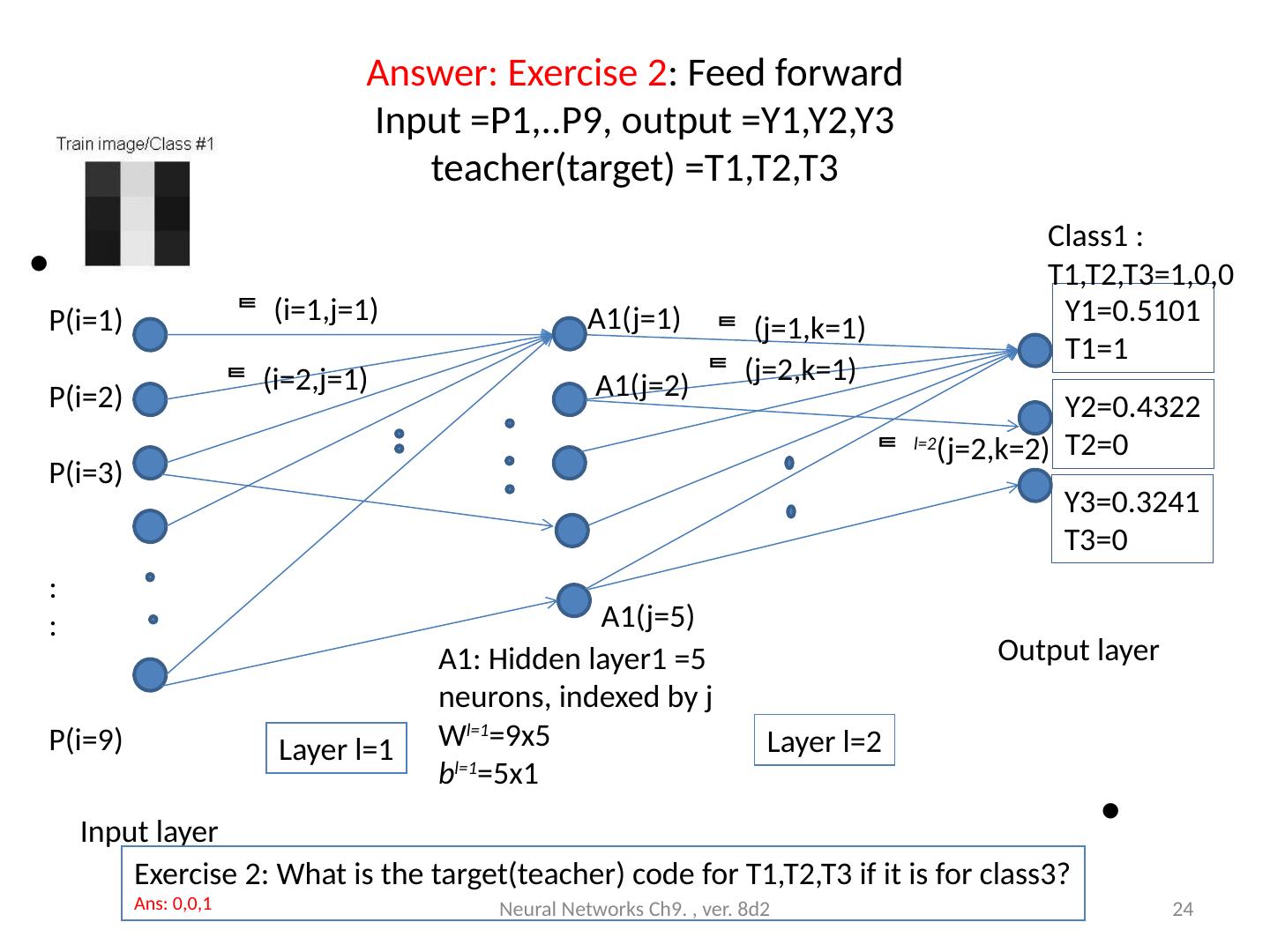
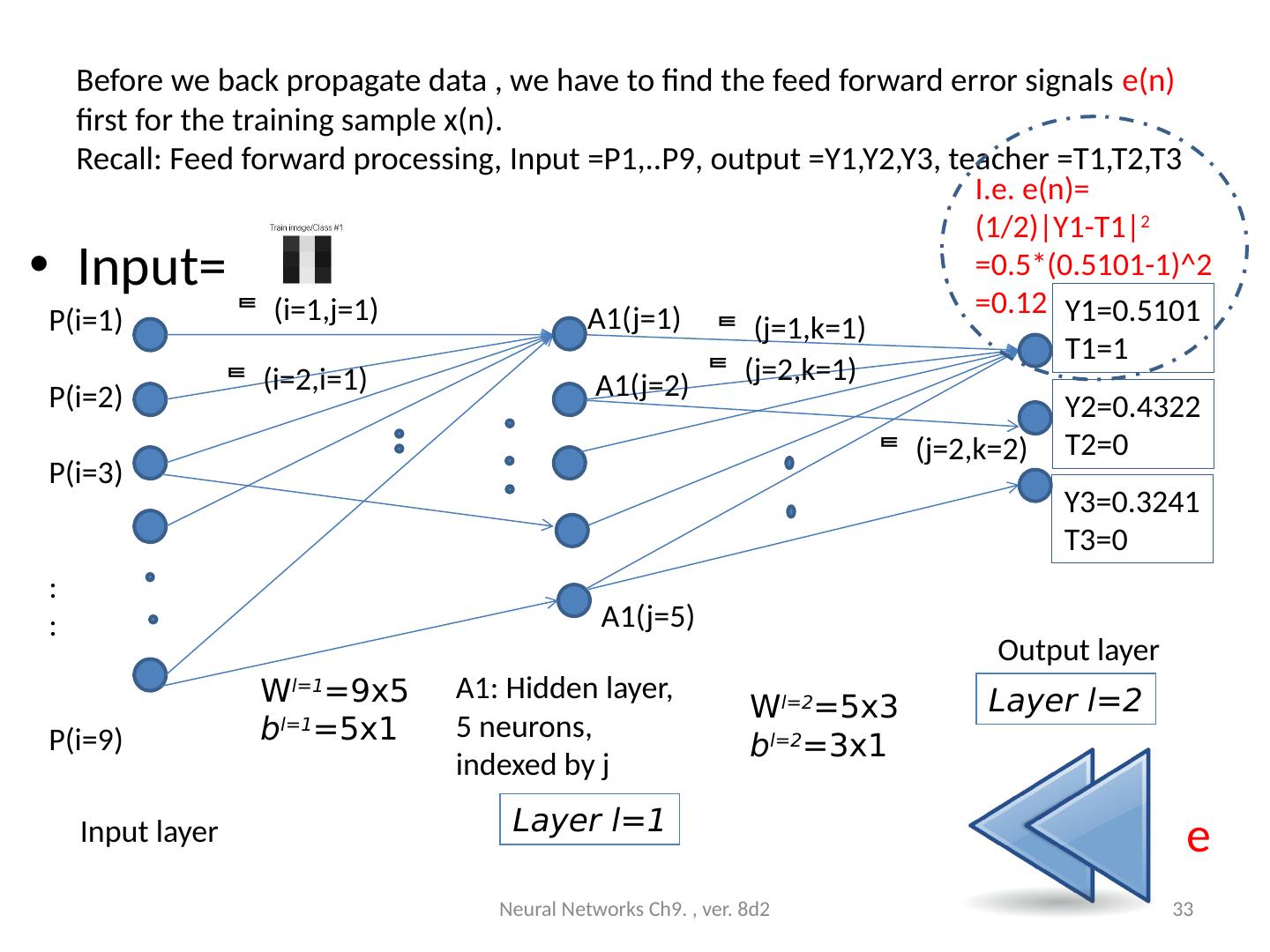
23 .Exercise 2: Feed forward Input =P1,..P9, output =Y1,Y2,Y3 teacher(target) =T1,T2,T3 Neural Networks Ch9. , ver. 8d2 23 A1: Hidden layer1 =5 neurons, indexed by j W l= 1 =9x5 b l= 1 =5x1 P(i=1) P(i=2) P(i=3) : : P(i=9)  (i=1,j=1)  ( i =2,j=1 ) A1(j=5) A1(j=1)  (j=1,k=1)  l=2 (j=2,k=2)  (j=2,k=1) A1(j=2) Layer l=1 Layer l=2 Y1=0.5101 T1=1 Y2=0.4322 T2=0 Y3=0.3241 T3=0 Output layer Input layer Class1 : T1,T2,T3=1,0,0 Exercise 2: What is the target (teacher) code for T1,T2,T3 if it is for class3? Answer:________________________

24 .Answer: Exercise 2 : Feed forward Input =P1,..P9, output =Y1,Y2,Y3 teacher(target) =T1,T2,T3 Neural Networks Ch9. , ver. 8d2 24 A1: Hidden layer1 =5 neurons, indexed by j W l= 1 =9x5 b l= 1 =5x1 P(i=1) P(i=2) P(i=3) : : P(i=9)  (i=1,j=1)  ( i =2,j=1 ) A1(j=5) A1(j=1)  (j=1,k=1)  l=2 (j=2,k=2)  (j=2,k=1) A1(j=2) Layer l=1 Layer l=2 Y1=0.5101 T1=1 Y2=0.4322 T2=0 Y3=0.3241 T3=0 Output layer Input layer Class1 : T1,T2,T3=1,0,0 Exercise 2: What is the target(teacher) code for T1,T2,T3 if it is for class3? Ans : 0,0,1

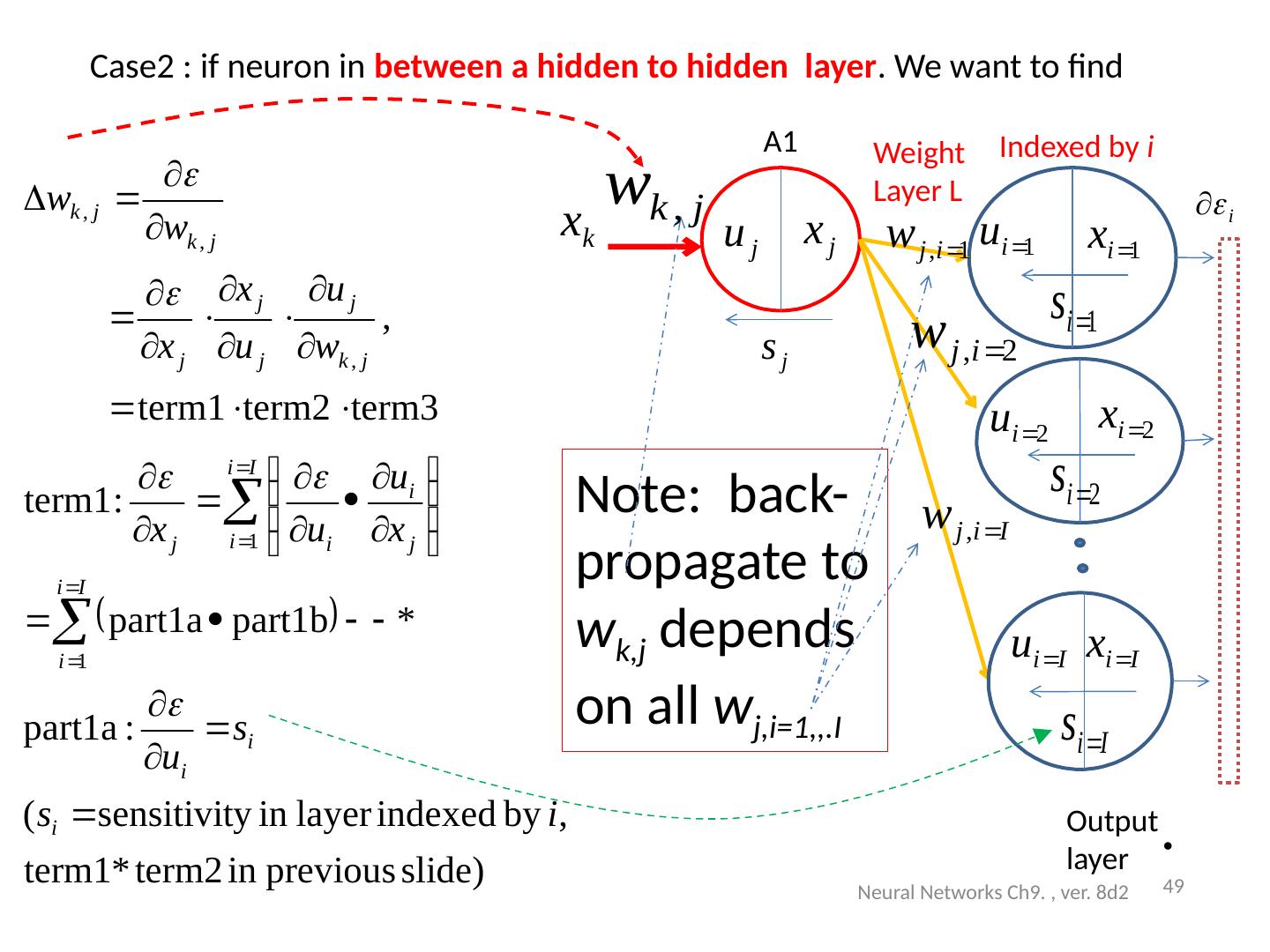
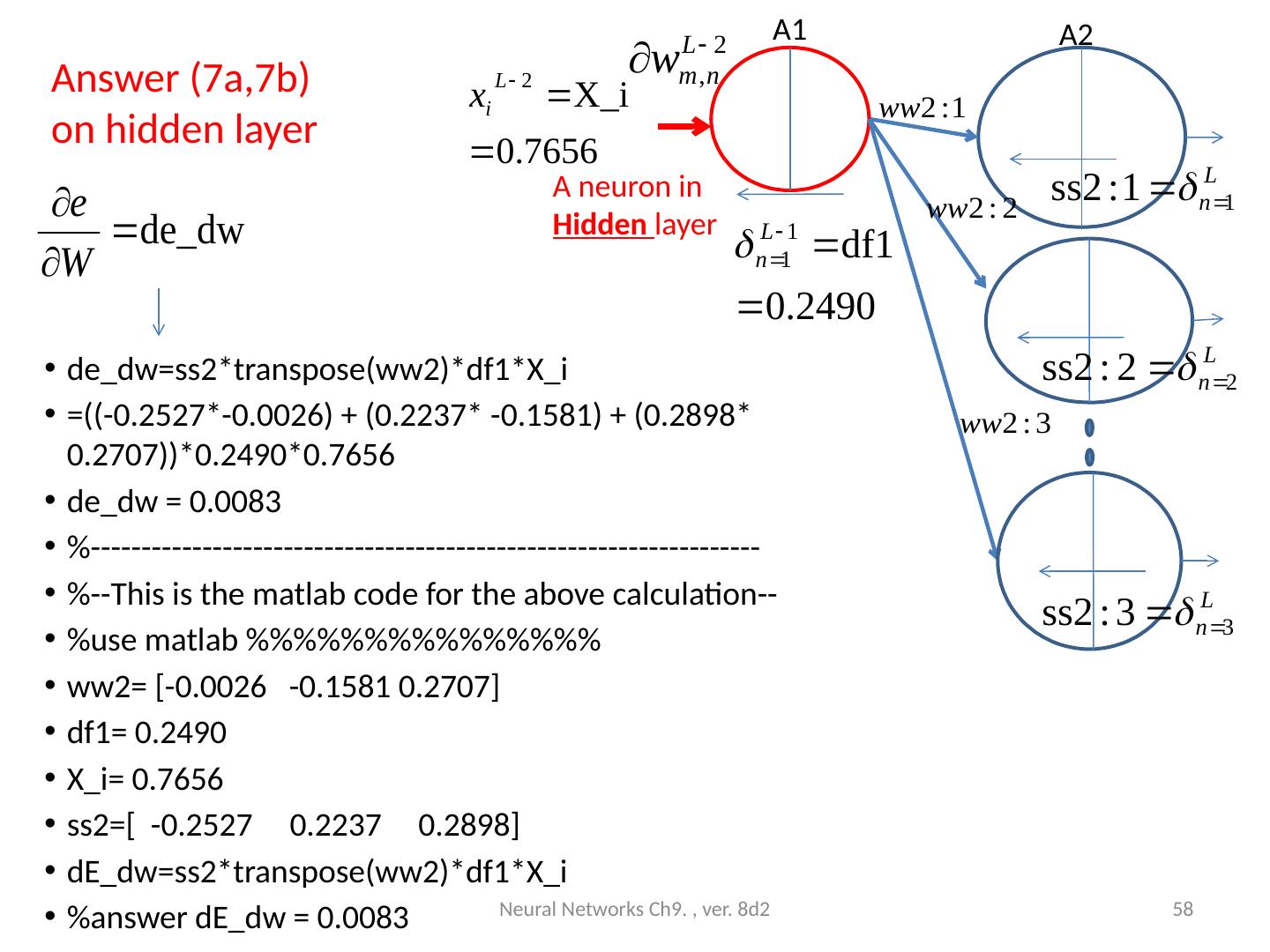
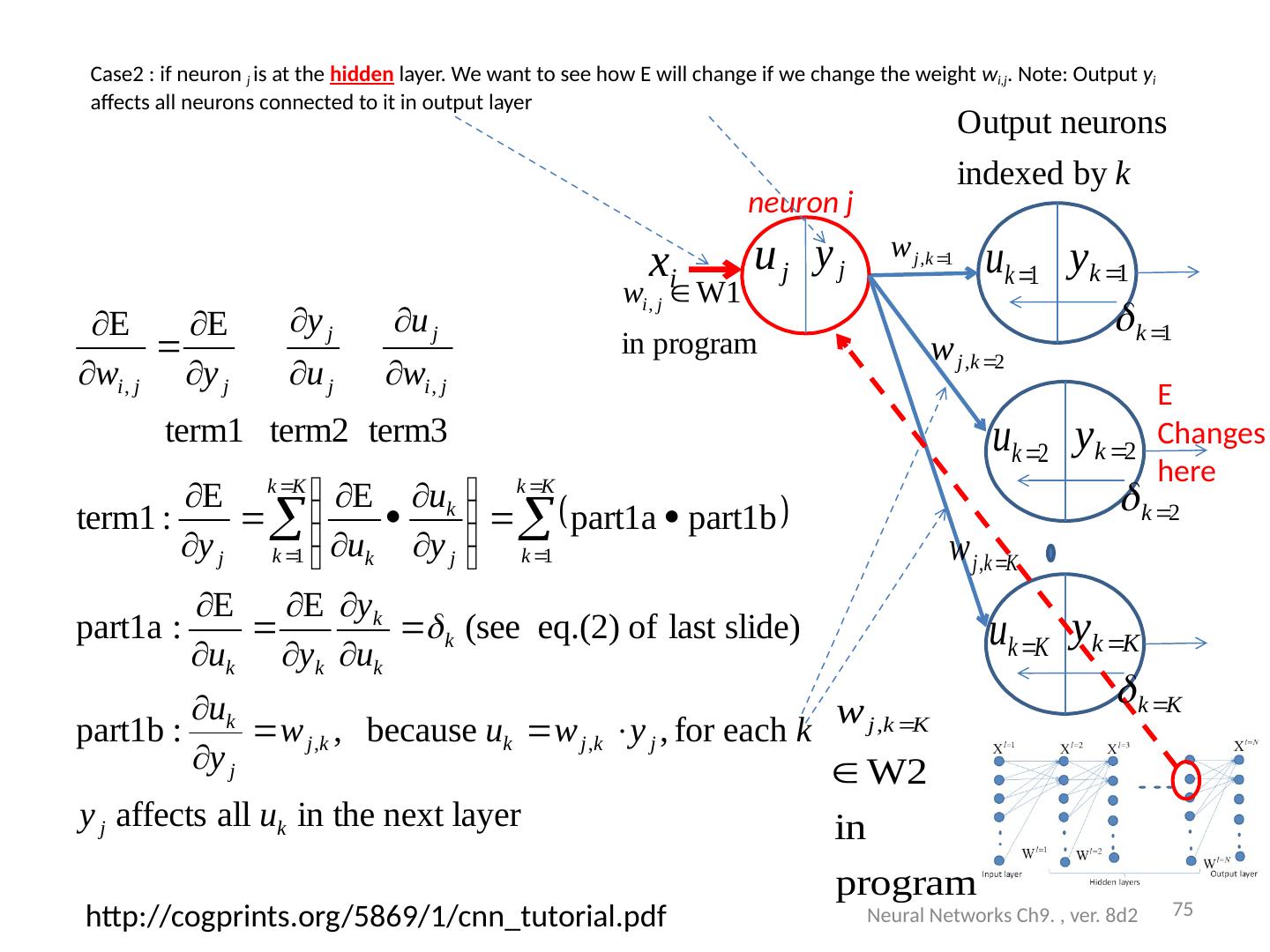
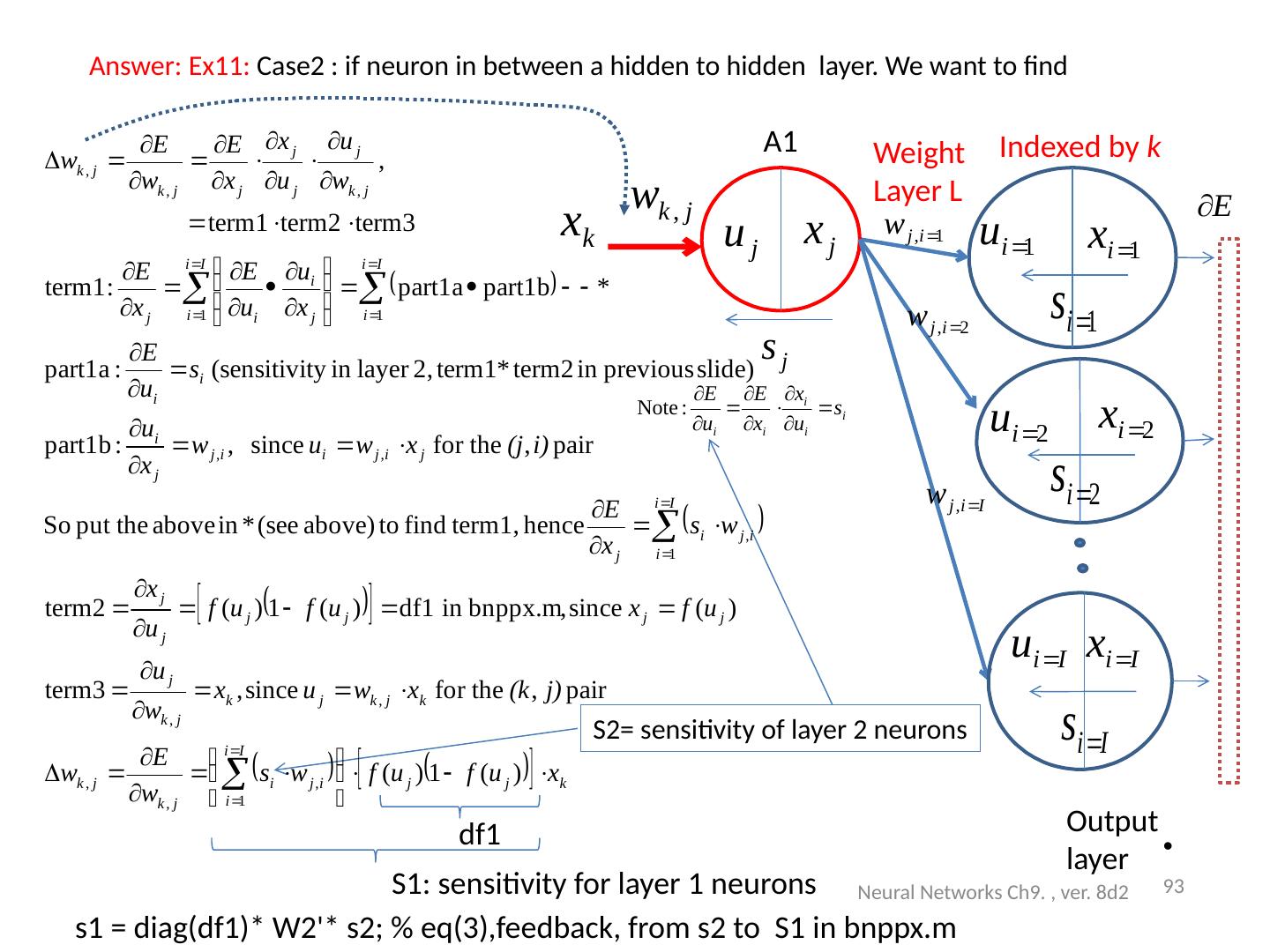
25 .Exercise 3. Given that Neural Networks Ch9. , ver. 8d2 25  l= 1 (i=1,j=1)  l= 1 (i=2,j=1)  l= 1 (i=9,j=1) P(i=1) P(i=2) P(i=9) Neuron i=1 Bias=b1(i=1)  l= 2 (i=1,k=1)  l= 2 (i=2,k=1)  l= 2 (i=5,k=1) A 2(k=2) A5 Neuron k=1 Bias=b2(k=1) A 1 (i=1)

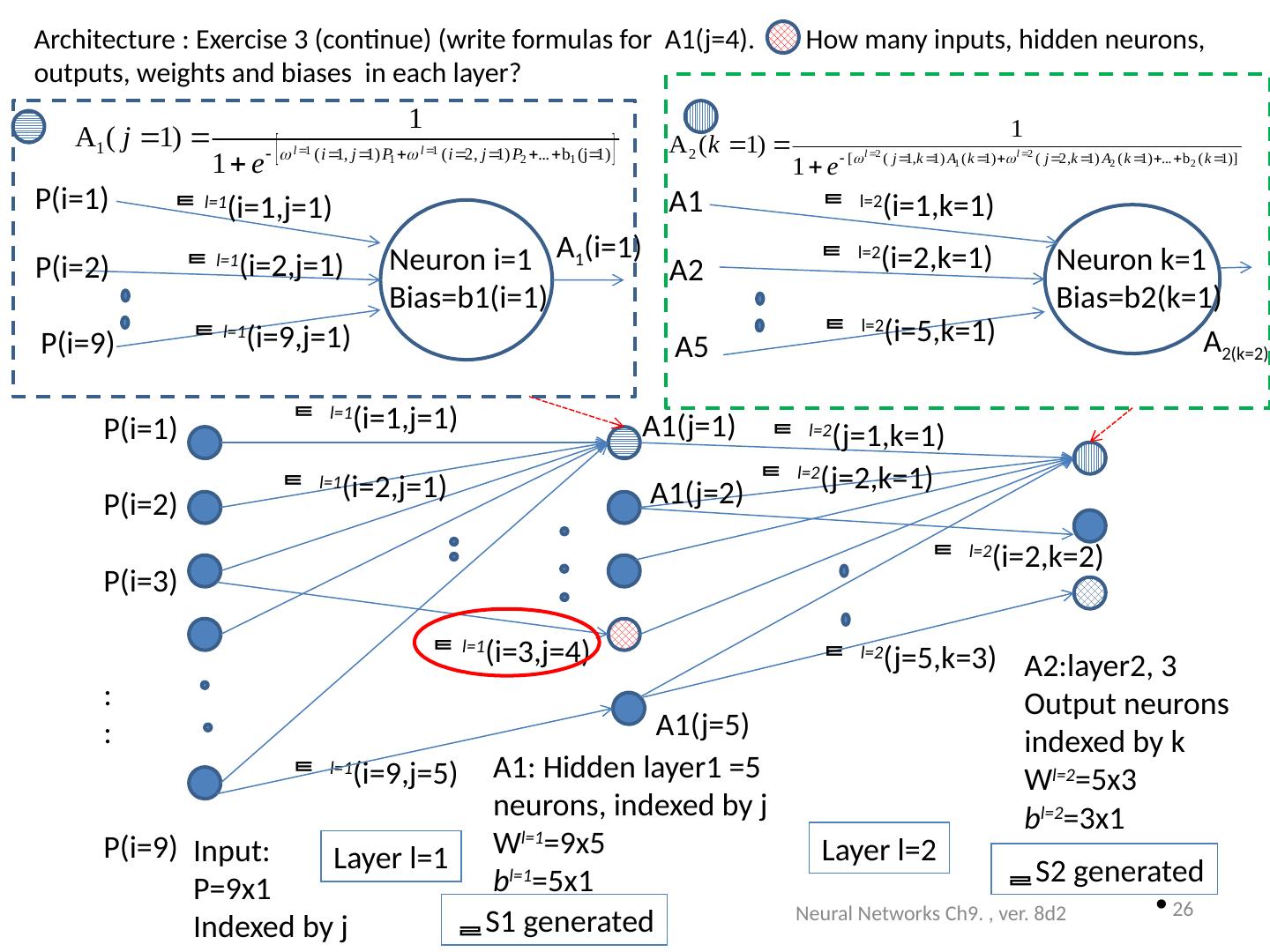
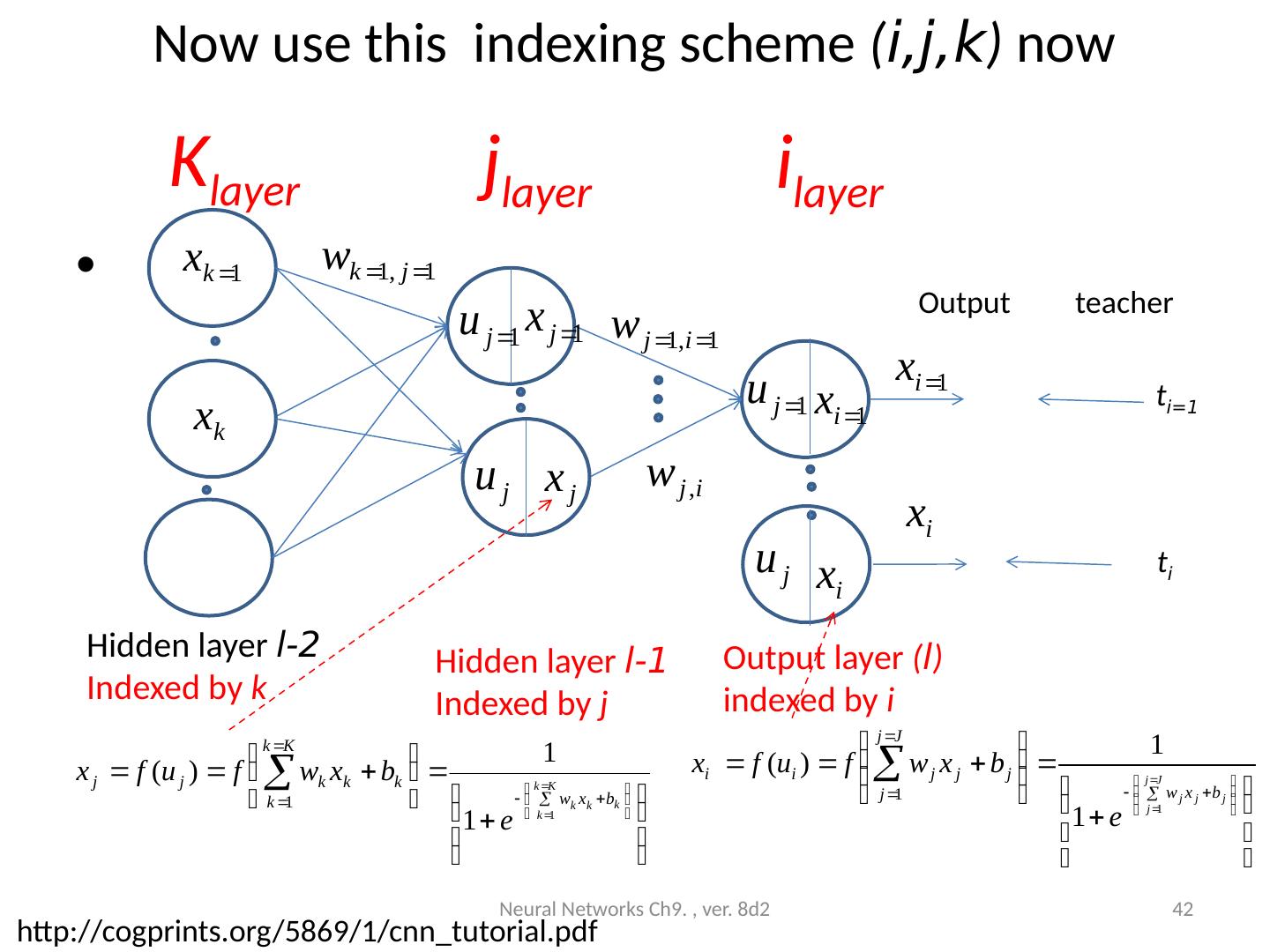
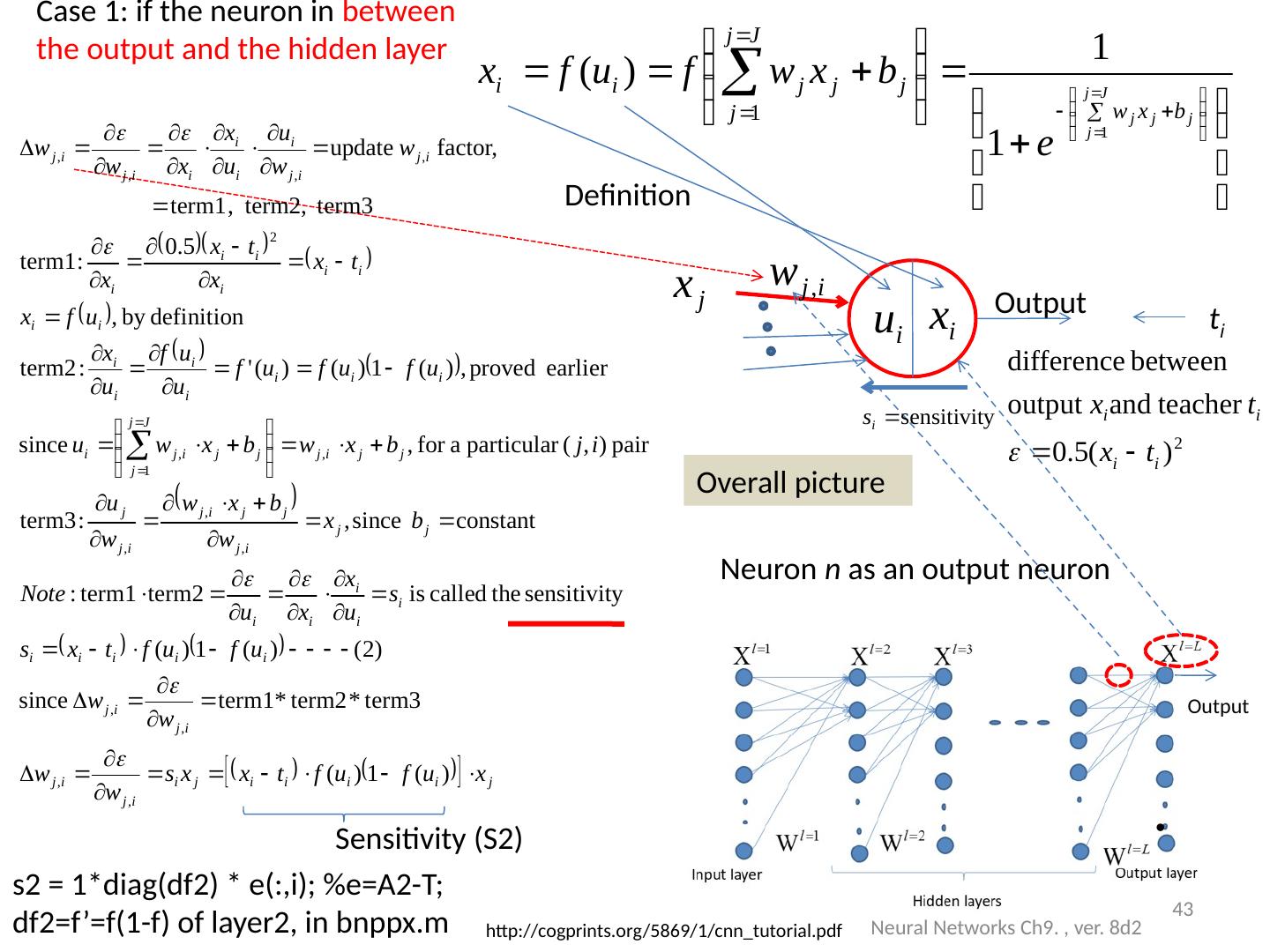
26 .Architecture : Exercise 3 (continue) (write formulas for A1( j =4). How many inputs, hidden neurons, outputs, weights and biases in each layer ? Neural Networks Ch9. , ver. 8d2 26 Input: P=9x1 Indexed by j A1: Hidden layer1 =5 neurons, indexed by j W l= 1 =9x5 b l= 1 =5x1  l= 1 (i=1,j=1)  l= 1 (i=2,j=1)  l= 1 (i=9,j=1) P(i=1) P(i=2) P(i=3) : : P(i=9) A 1 (i=1) P(i=1) P(i=2) P(i=9) Neuron i=1 Bias=b1(i=1)  l= 2 (i=1,k=1)  l= 2 (i=2,k=1)  l= 2 (i=5,k=1) A 2(k=2) A1 A2 A5 Neuron k=1 Bias=b2(k=1)  l= 1 (i=1,j=1)  l= 1 (i=2,j=1)  l= 1 (i=9,j=5)  l= 1 (i=3,j=4) A1(j=5) A1(j=1) A2:layer2, 3 Output neurons indexed by k W l=2 =5x3 b l=2 =3x1  l=2 (j=5,k=3)  l=2 (j=1,k=1)  l=2 (i=2,k=2)  l=2 (j=2,k=1) A1(j=2) Layer l=1 Layer l=2  S2 generated  S1 generated

27 .Answer (exercise3: write values for A1( i =4) Example: if P=[ 0.7656 0.7344 0.9609 0.9961 0.9141 0.9063 0.0977 0.0938 0.0859]%each is p(j=1,2,3..) W l =1 =[ 0.2112 0.1540 -0.0687 -0.0289 0.0720 -0.1666 0.2938 -0.0169 -0.1127]%each is w(l=1,j=1,2,3,..) b l =1 = 0.1441 %for neuron i %Find A1( i =4) A1_i_is_4=1/(1+exp[-(  l=1 * P+ b l =1 ))] =0.49. How many inputs, hidden neurons, outputs, weights and biases in each layer? Answer: Inputs=9, hidden neurons=5, outputs=3, weights in hidden layer (layer1) =9x5, neurons in output layer (layer2)= 5x3, 5 biases in hidden layer (layer1), 3 biases in output layer (layer2) The 4 th neuron in the hidden layer is A 1 ( i =4) Neural Networks Ch9. , ver. 8d2 27

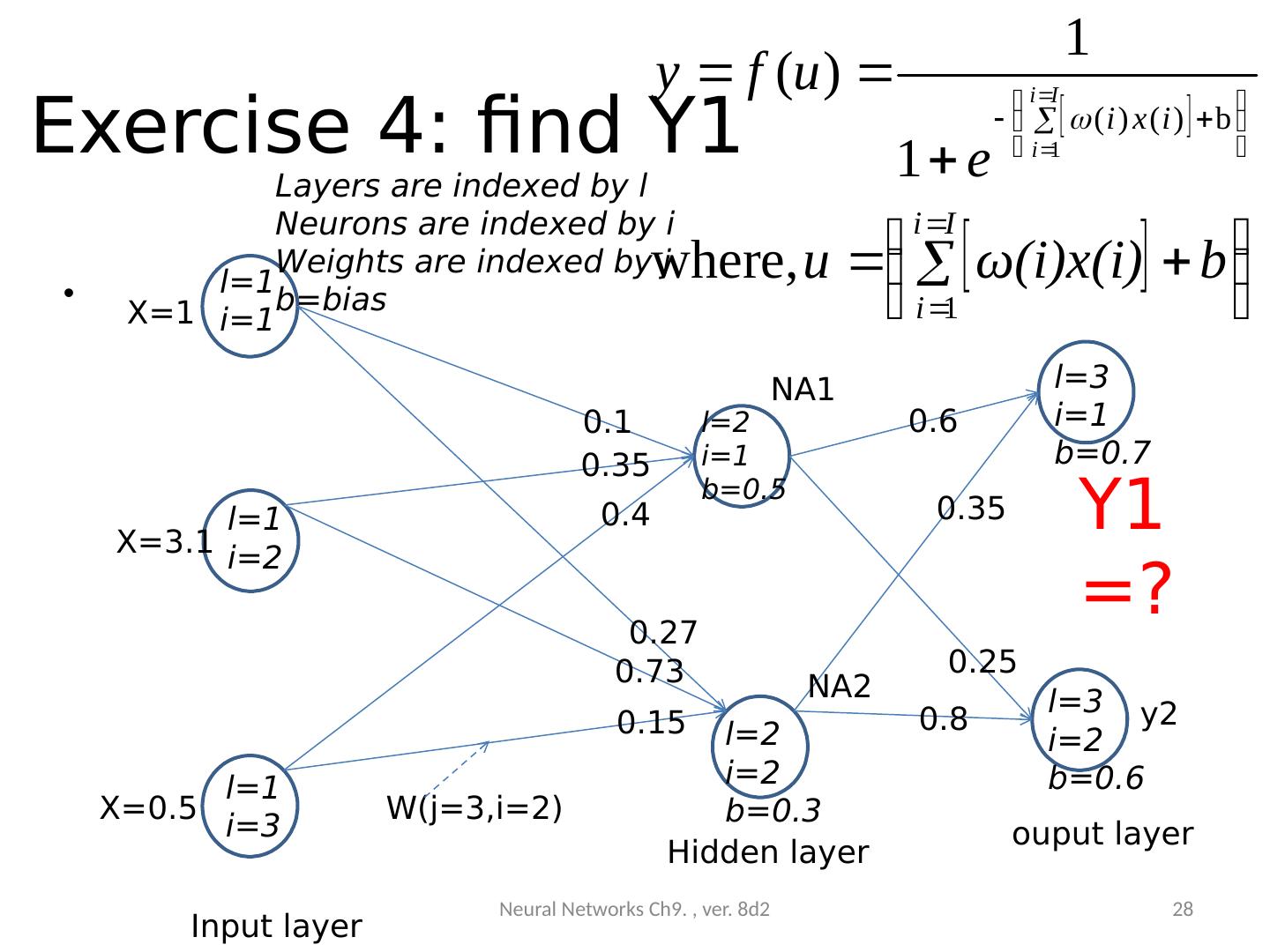
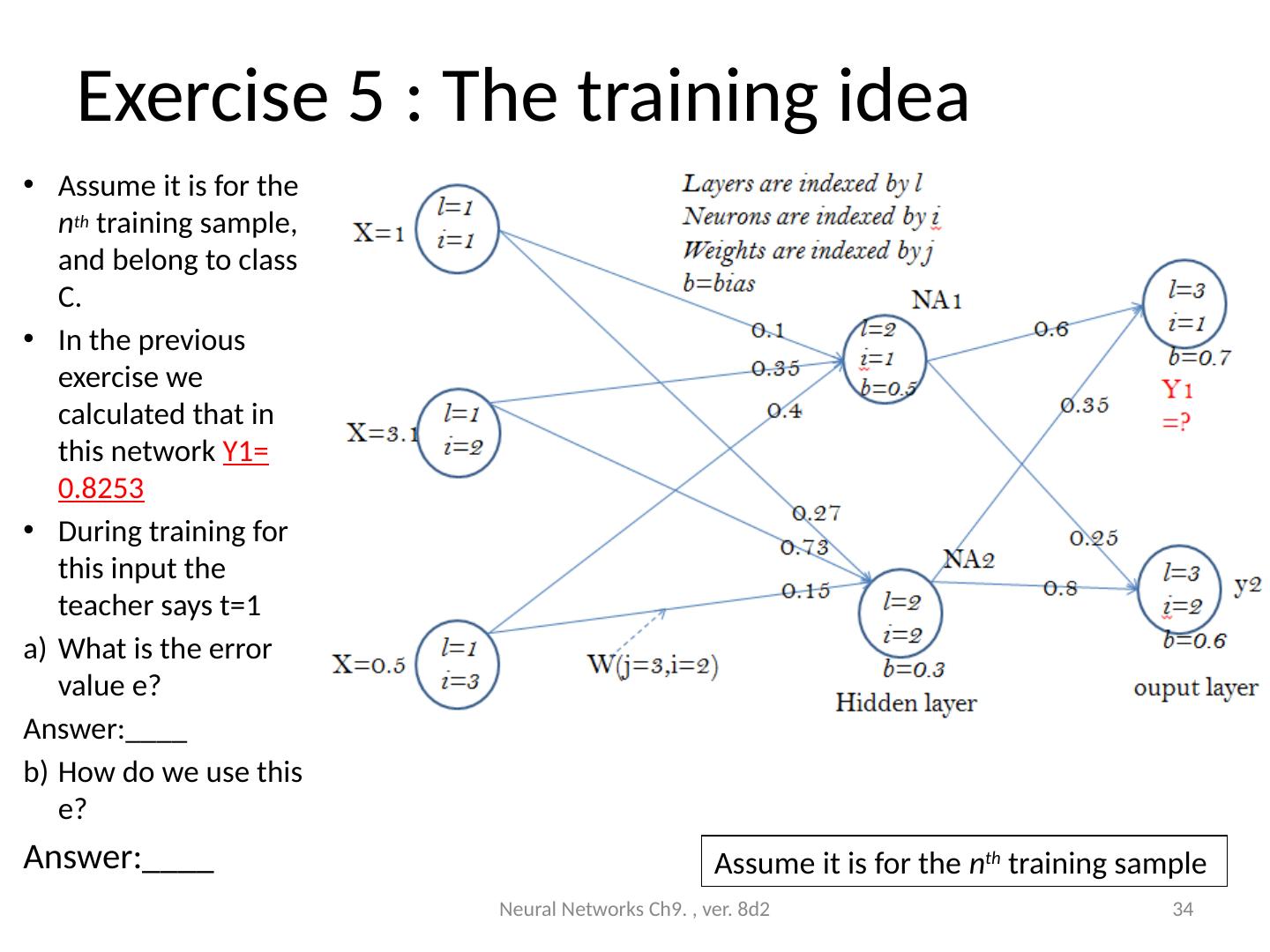
28 .Exercise 4: find Y1 Neural Networks Ch9. , ver. 8d2 28 l=1 i=2 l=1 i=3 l=1 i=1 l=2 i =1 b=0.5 l=2 i=2 b=0.3 l=3 i=1 b=0.7 l=3 i =2 b=0.6 W(j=3,i=2) 0.15 0.73 0.27 0.1 0.35 0.4 0.6 0.35 0.8 0.25 Input layer Hidden layer ouput layer Y1 =? y2 X=1 X=3.1 X=0.5 NA1 NA2 Layers are indexed by l Neurons are indexed by i Weights are indexed by j b=bias

29 .Answer 4 % u1=1*0.1+3.1*0.35+0.5*0.4+0.5 NA1=1/(1+exp(-1*u1)) %NA1=0.8682 u2=1*0.27+3.1*0.73+0.5*0.15+0.3 NA2=1/(1+exp(-1*u2)) %NA2=0.9482 u_Y1=NA1*0.6+NA2*0.35+0.7 Y1=1/(1+exp(-1*u_Y1)) %Y1= 0.8253 Neural Networks Ch9. , ver. 8d2 29