06_Adaboost for building robust classifiers

1 .Ch. 6: Adaboost for building robust classifiers KH Wong Adaboost , V8b 1

2 .Overview Objectives of AdaBoost Solve 2-class classification problems Will discuss Training Detection Examples Adaboost , V8b 2

3 .Objective Automatically classify inputs into different categories of similar features Example Spam mail detection and filtering Face detection: find the faces in the input image Vision based gesture recognition [Chen 2007] Adaboost , V8b 3

4 .Different detection problems Two-class problem (will be discussed here) E.g. face detection In a picture, are there any faces or no face? Multi-class problems (Not discussed here) Adaboost can be extended to handle multi class problems In a picture, are there any faces of men , women, children ? (Still an unsolved problem) Adaboost , V8b 4

5 .Define a 2-class classifier :its method and procedures Supervised training Show many positive samples (face) to the system Show many negative samples (non-face) to the system. Learn the parameters and construct the final strong classifier. Detection Given an unknown input image, the system can tell if there are faces or not. Adaboost , V8b 5

6 .We will learn Training procedures Give +ve and –ve examples to the system, then the system will learn to classify an unknown input. E.g. give pictures of faces (+ve examples) and non-faces (-ve examples) to train the system. Detection procedures Input an unknown (e.g. an image) , the system will tell you it is a face or not. Adaboost , V8b 6 Face non-face

7 .Exercise 1 :A linear programming example A line y= mx+c m=3, c=2 (a) W hen x=1, y=3*x+2=5. So when y’=5.5, i s ( x,y ’) above[i]/below[ii] the line? Answer: [i] or [ii]?________ (a) When x=0, y=3*x+2=2. So when y”=1.5 , is ( x,y ”) above[i]/below[ii] the line? Answer : [i] or [ii]?________ Conclusion, if a point ( x,y ) is above and on the left of the line y= mx+c , y> mx+c if a ( x,y ) is below and on the right side of the line y= mx+c , y< mx+c Adaboost , V8b 7 y-axis X-axis y=mx+c x=0,y=2 x=1,y=5 x=-1,y=-1 y-mx>c y-mx<c

8 .ANSWER 1 :A linear programming example A line y= mx+c m=3, c=2 (a) W hen x=1, y=3*x+2=5. So when y’=5.5, i s ( x,y ’) above[i]/below[ii] the line? Answer: [i] or [ii]?_ i above (a) When x=0, y=3*x+2=2. So when y”=1.5 , is ( x,y ”) above[i]/below[ii] the line? Answer : [i] or [ii ]?_ ii below Conclusion, if a point ( x,y ) is above and on the left of the line y= mx+c , y> mx+c if a ( x,y ) is below and on the right side of the line y= mx+c , y< mx+c Adaboost , V8b 8 y-axis X-axis y=mx+c x=0,y=2 x=1,y=5 x=-1,y=-1 y-mx>c y-mx<c

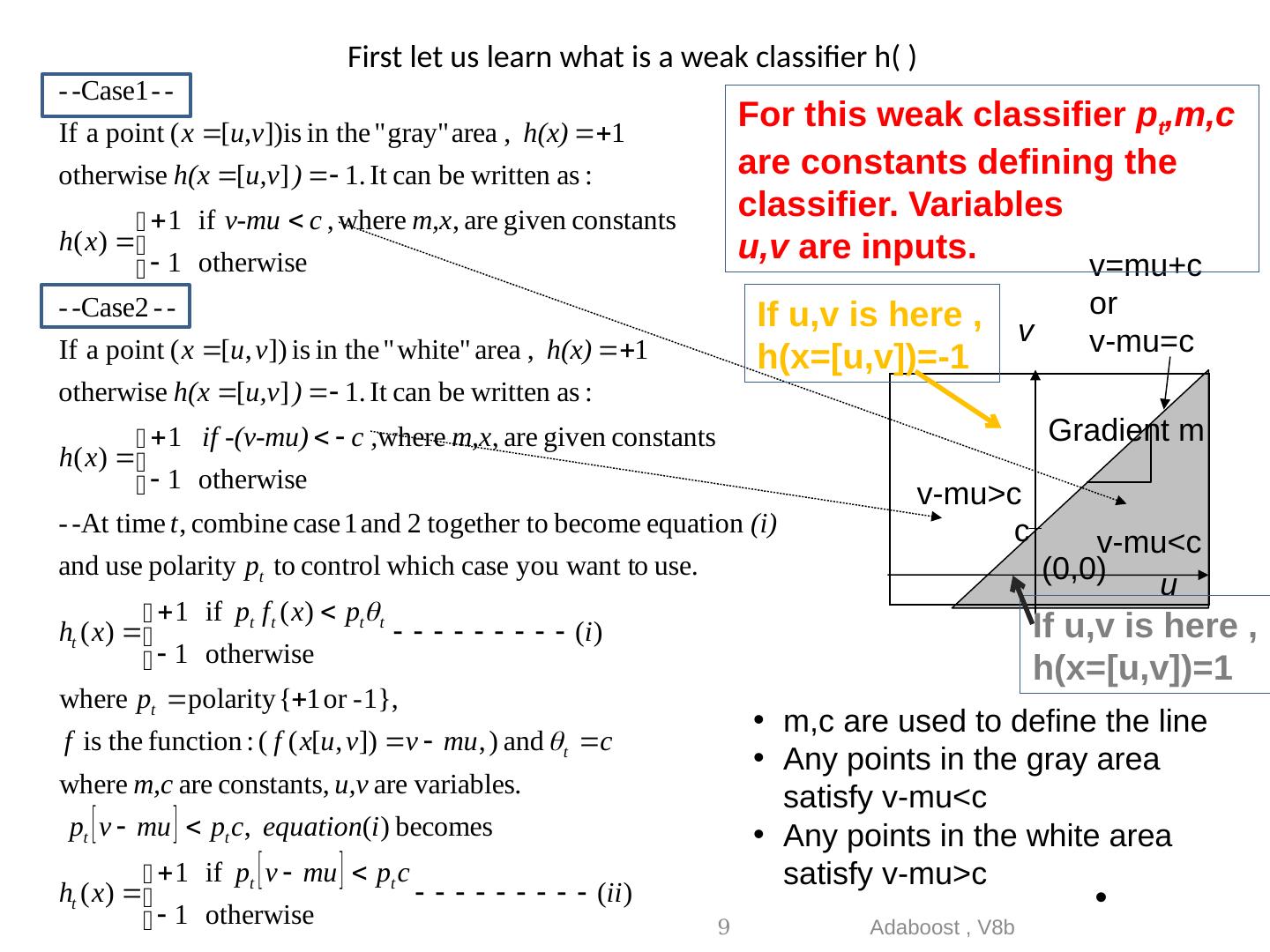
9 .First let us learn what is a weak classifier h( ) Adaboost , V8b 9 v=mu+c or v-mu=c m,c are used to define the line Any points in the gray area satisfy v-mu<c Any points in the white area satisfy v-mu>c v c Gradient m (0,0) v-mu<c v-mu>c u For this weak classifier p t ,m,c are constants defining the classifier. Variables u,v are inputs. If u ,v is here , h(x=[ u,v ])=1 If u ,v is here , h(x=[ u,v ])=-1

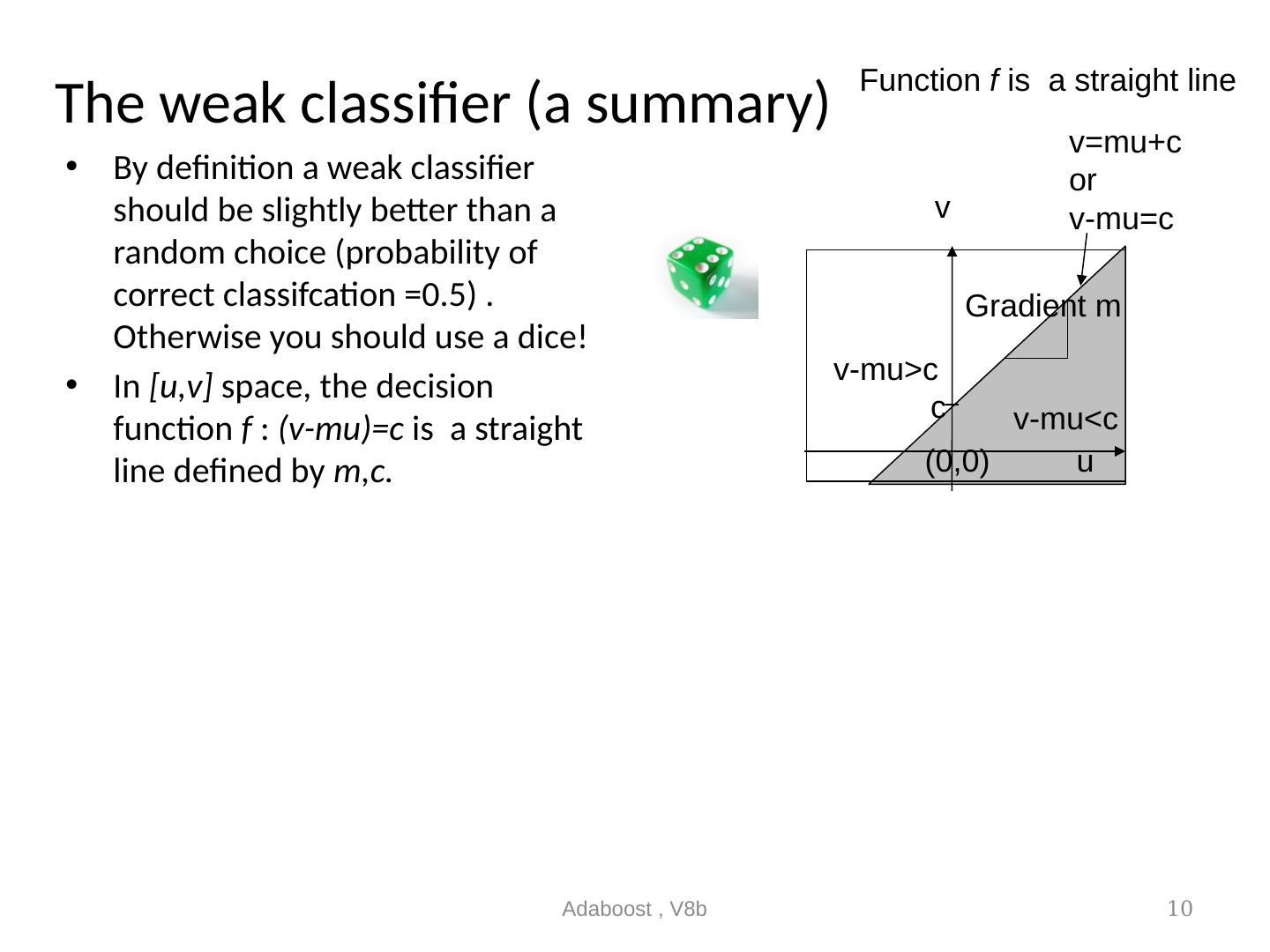
10 .The weak classifier (a summary) By definition a weak classifier should be slightly better than a random choice (probability of correct classifcation =0.5) . Otherwise you should use a dice! In [u,v] space, the decision function f : (v-mu)=c is a straight line defined by m,c. Adaboost , V8b 10 Function f is a straight line v c Gradient m (0,0) v-mu<c v-mu>c u v=mu+c or v-mu=c

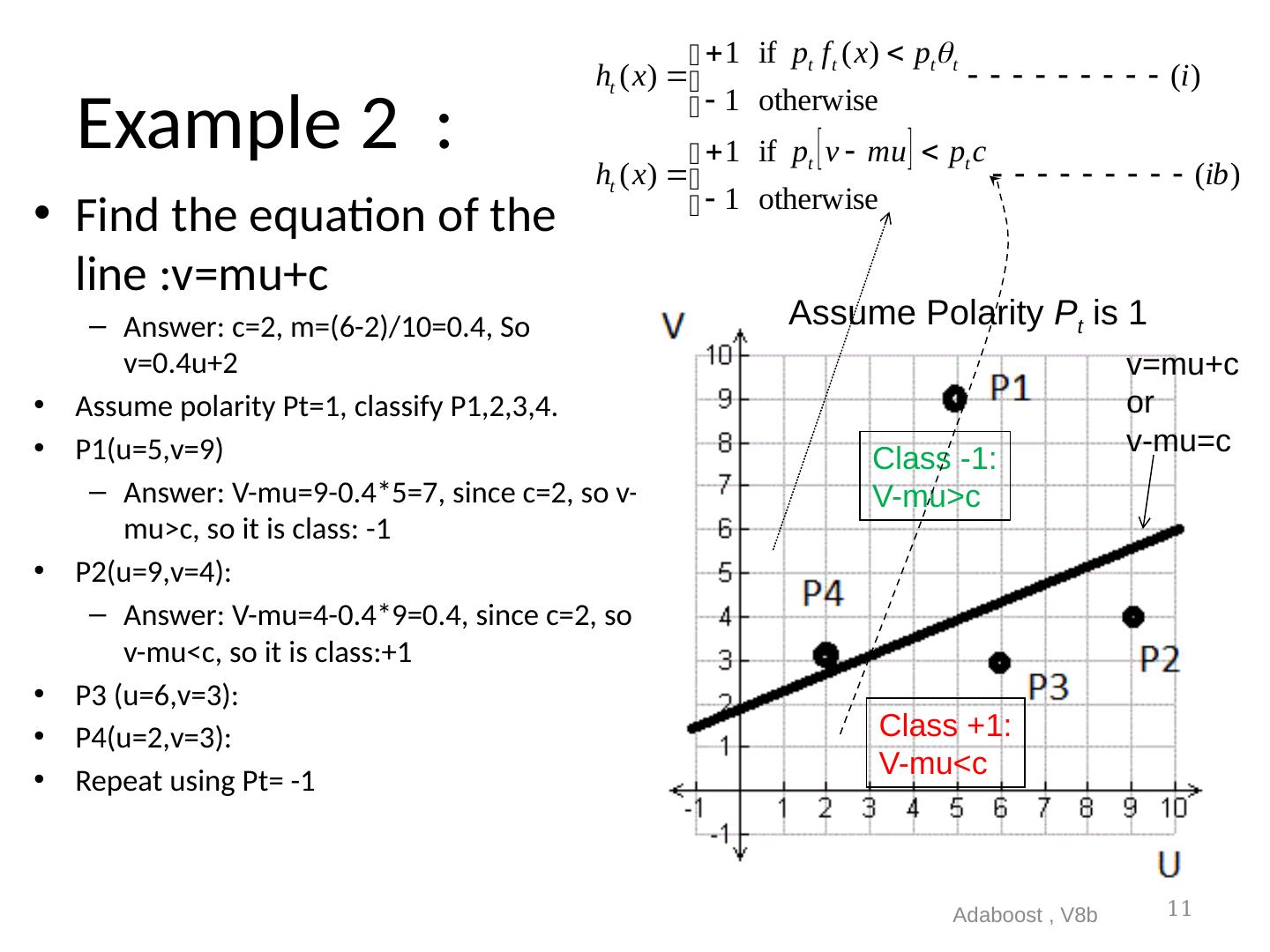
11 .Example 2 : Find the equation of the line :v= mu+c Answer: c=2, m=(6-2)/10=0.4, So v=0.4u+2 Assume polarity Pt=1, classify P1,2,3,4. P1(u=5,v=9) Answer: V-mu=9-0.4*5=7, since c=2, so v-mu>c, so it is class: -1 P2(u=9,v=4): Answer: V-mu=4-0.4*9=0.4, since c=2, so v-mu<c, so it is class:+1 P3 (u=6,v=3): P4(u=2,v=3): Repeat using Pt= -1 Adaboost , V8b 11 Class +1: V-mu<c Class -1: V-mu>c Assume Polarity P t is 1 v=mu+c or v-mu=c

12 .Answer for exercise 2 P3(u=6,v=3): V-mu=3-0.4*6=0.6, since c=2, so v-mu<c, so it is class +1 P4(u=2,v=3): V-mu=3-0.4*2=2.2, since c=2, so v-mu>c, so it is class -1 Adaboost , V8b 12

13 .Learn what is h( ), a weak classifier. Decision stump Decision stump definition A decision stump is a machine learning model consisting of a one-level decision tree . [1] That is, it is a decision tree with one internal node (the root) which is immediately connected to the terminal nodes. A decision stump makes a prediction based on the value of just a single input feature. Sometimes they are also called 1-rules . [2] From http://en.wikipedia.org/wiki/Decision_stump Example Adaboost , V8b 13 Temperature T T<=10 o c 10 o c<T<28 o c T>= 28 0 c Cold mild hot

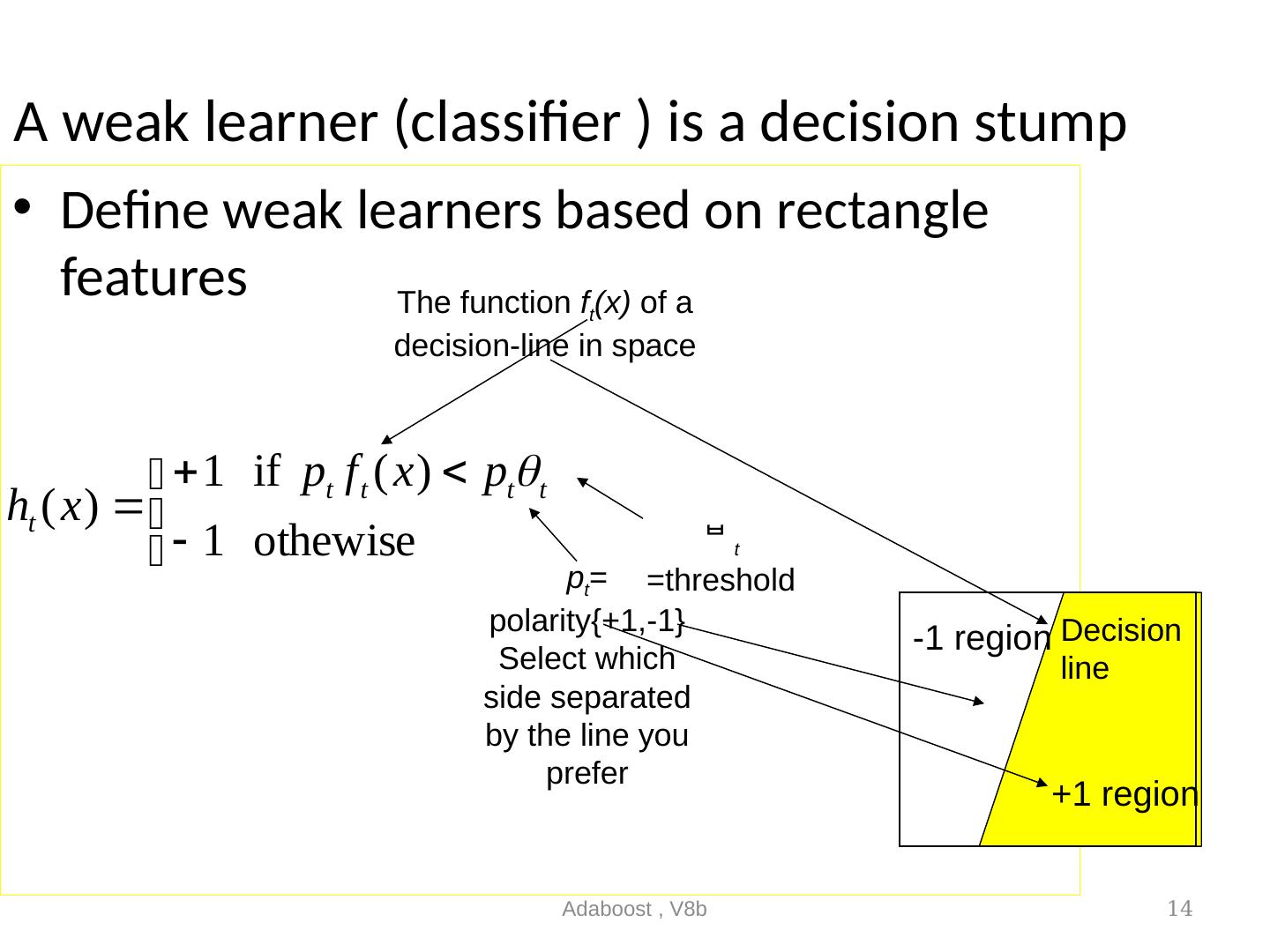
14 .Adaboost , V8b 14 A weak learner (classifier ) is a decision stump Define weak learners based on rectangle features The function f t (x) of a decision-line in space p t = polarity{+1,-1} Select which side separated by the line you prefer  t =threshold Decision line +1 region -1 region

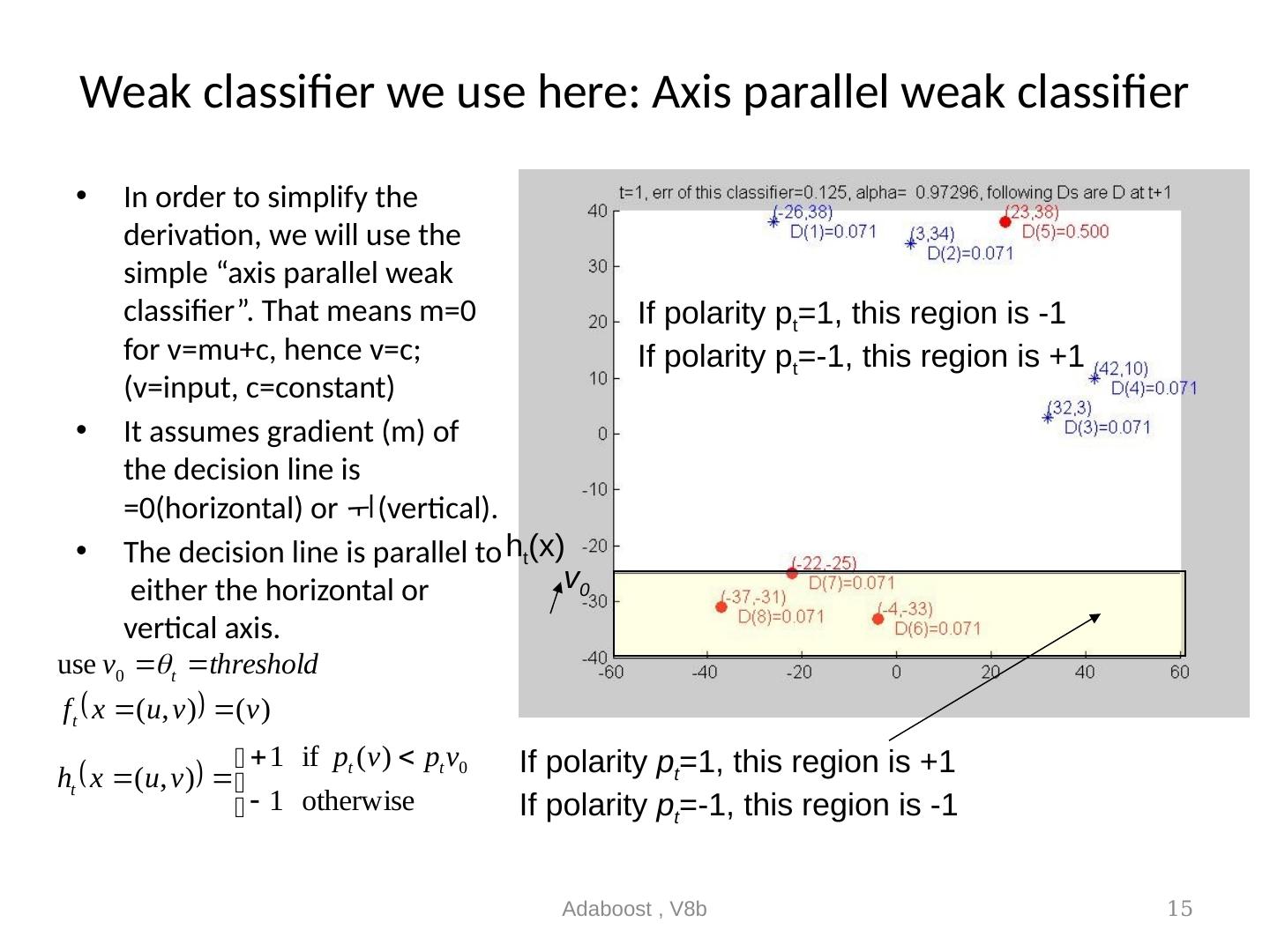
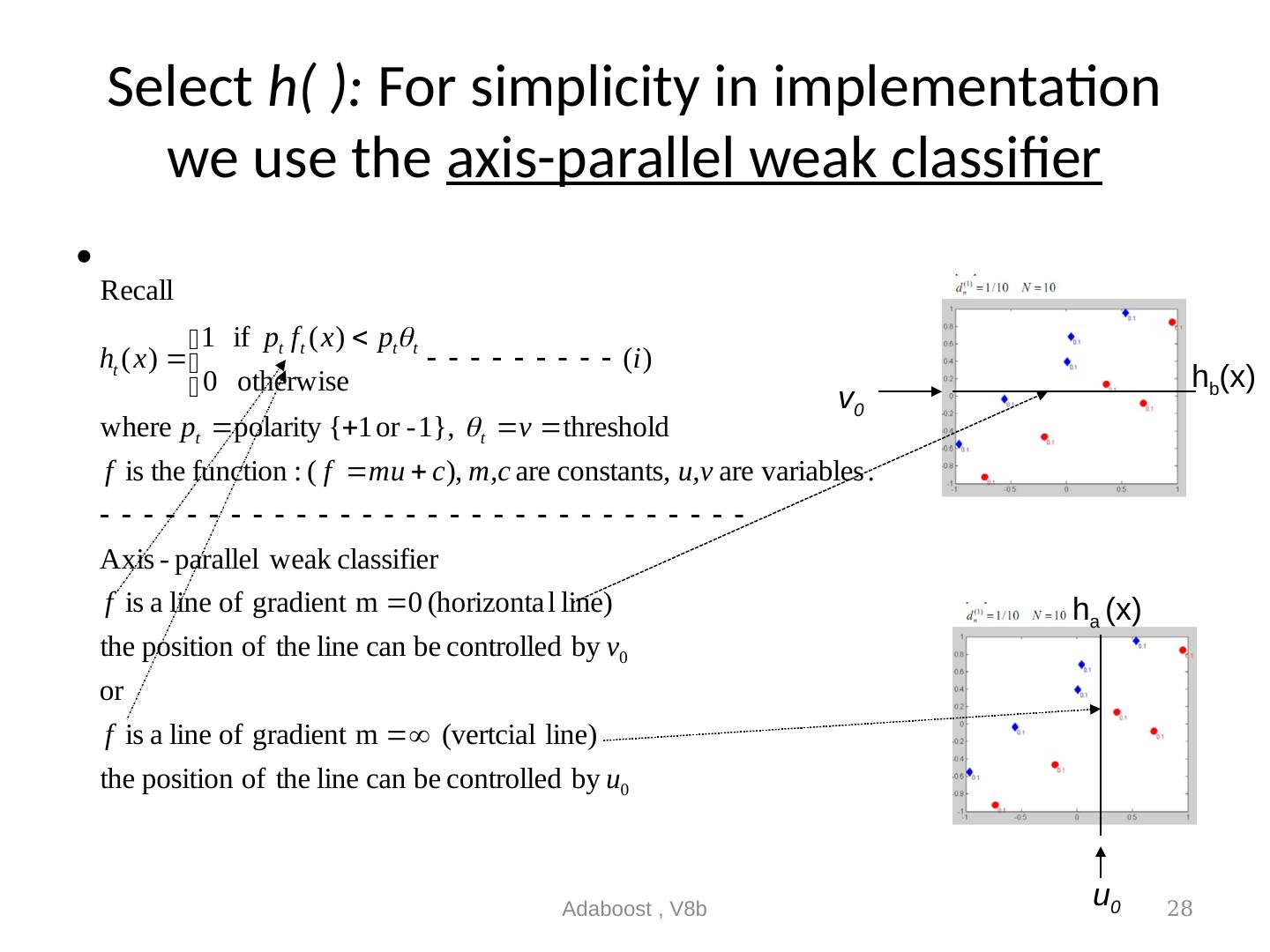
15 .Weak classifier we use here: Axis parallel weak classifier In order to simplify the derivation, we will use the simple “axis parallel weak classifier”. That means m=0 for v= mu+c , hence v=c; (v=input, c=constant) It assumes gradient (m) of the decision line is =0(horizontal) or (vertical). The decision line is parallel to either the horizontal or vertical axis. Adaboost , V8b 15 h t (x) v 0 If polarity p t =1, this region is +1 If polarity p t =-1, this region is -1 If polarity p t =1, this region is -1 If polarity p t =-1, this region is +1

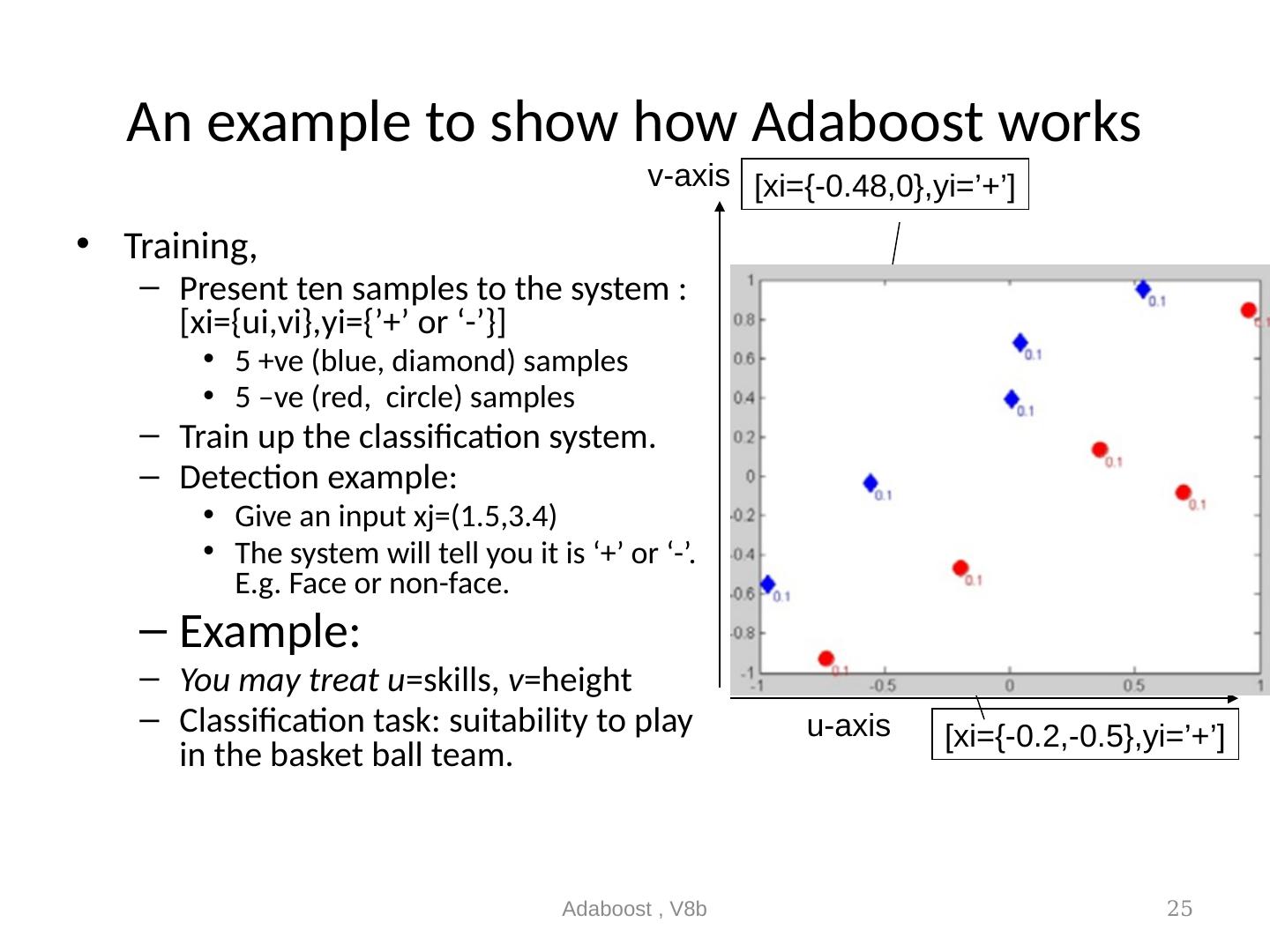
16 .An example to show how Adaboost works Training, Present ten samples to the system :[xi={ui,vi},yi={’+’ or ‘-’}] 5 +ve (blue, diamond) samples 5 –ve (red, circle) samples Train up the system Detection Give an input xj=(1.5,3.4) The system will tell you it is ‘+’ or ‘-’. E.g. Face or non-face Example: u = weight , v =height Classification: suitability to play in the boxing. Adaboost , V8b 16 [xi={-0.48,0},yi=’+’] [xi={-0.2,-0.5},yi=’+’] u-axis v-axis

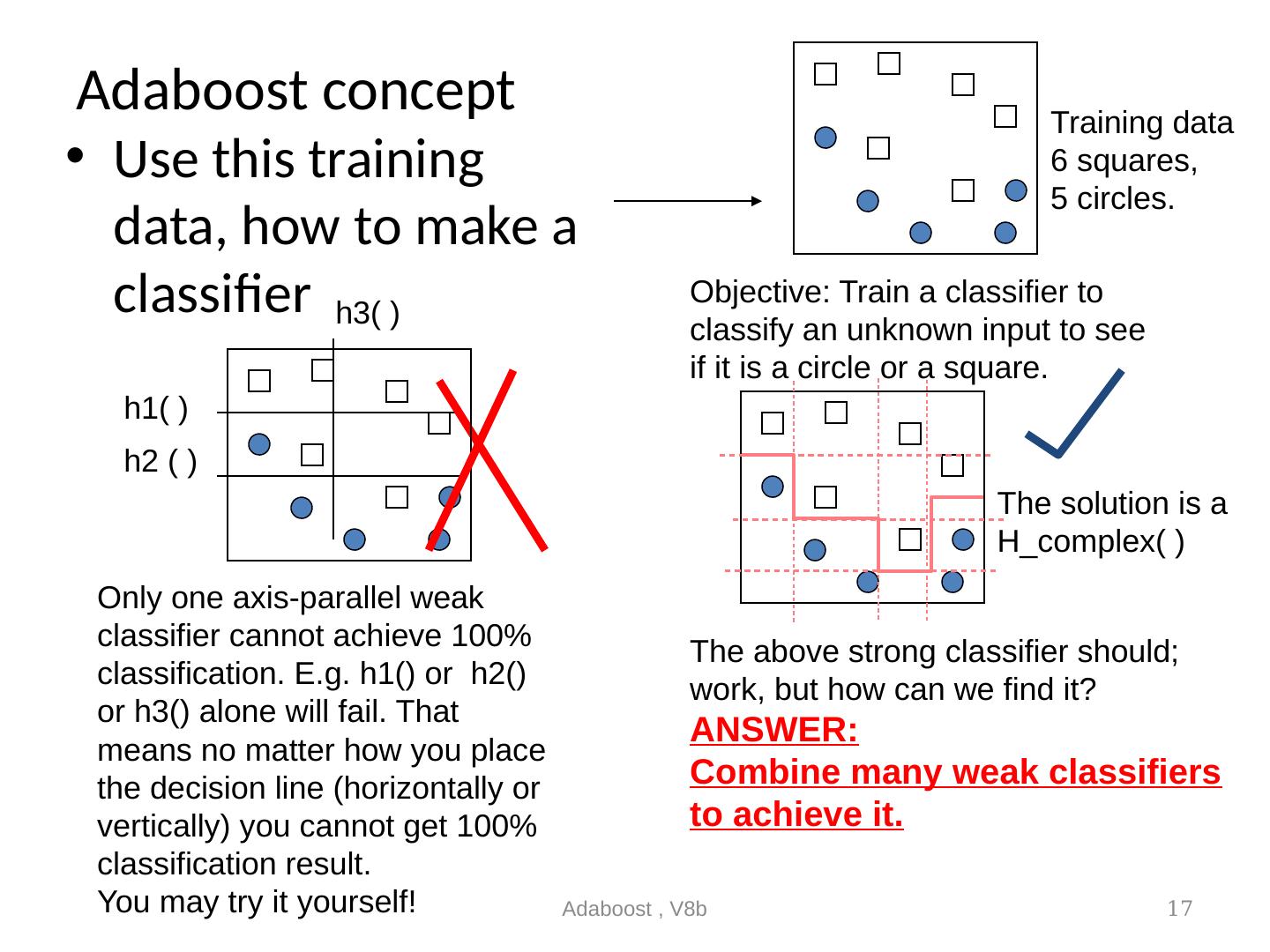
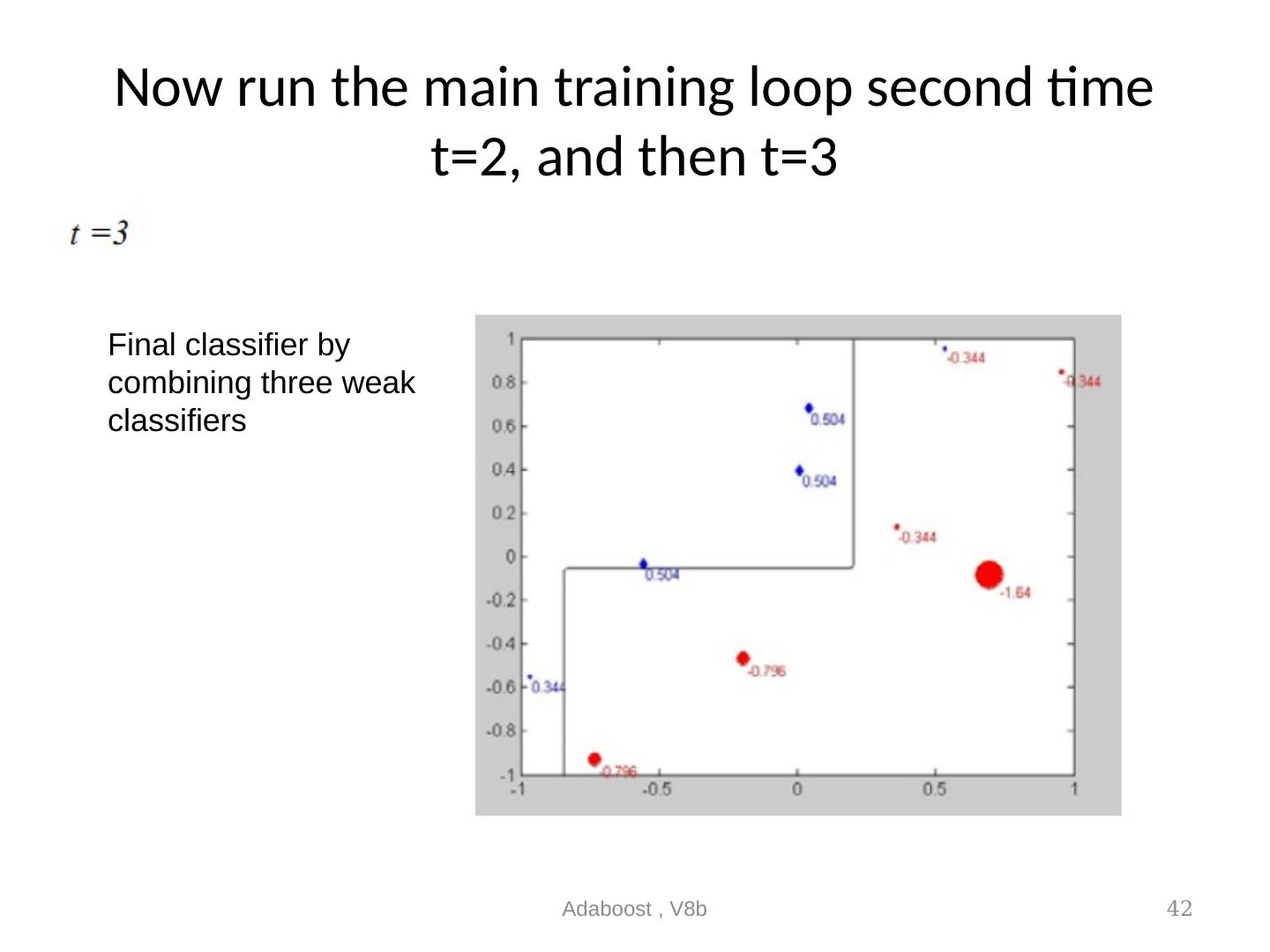
17 .Adaboost concept Use this training data, how to make a classifier Adaboost , V8b 17 Only one axis-parallel weak classifier cannot achieve 100% classification. E.g. h1() or h2() or h3() alone will fail. That means no matter how you place the decision line (horizontally or vertically) you cannot get 100% classification result. You may try it yourself! The above strong classifier should; work, but how can we find it? ANSWER: Combine many weak classifiers to achieve it. Training data 6 squares, 5 circles. h1( ) h2 ( ) h3( ) The solution is a H_complex( ) Objective: Train a classifier to classify an unknown input to see if it is a circle or a square.

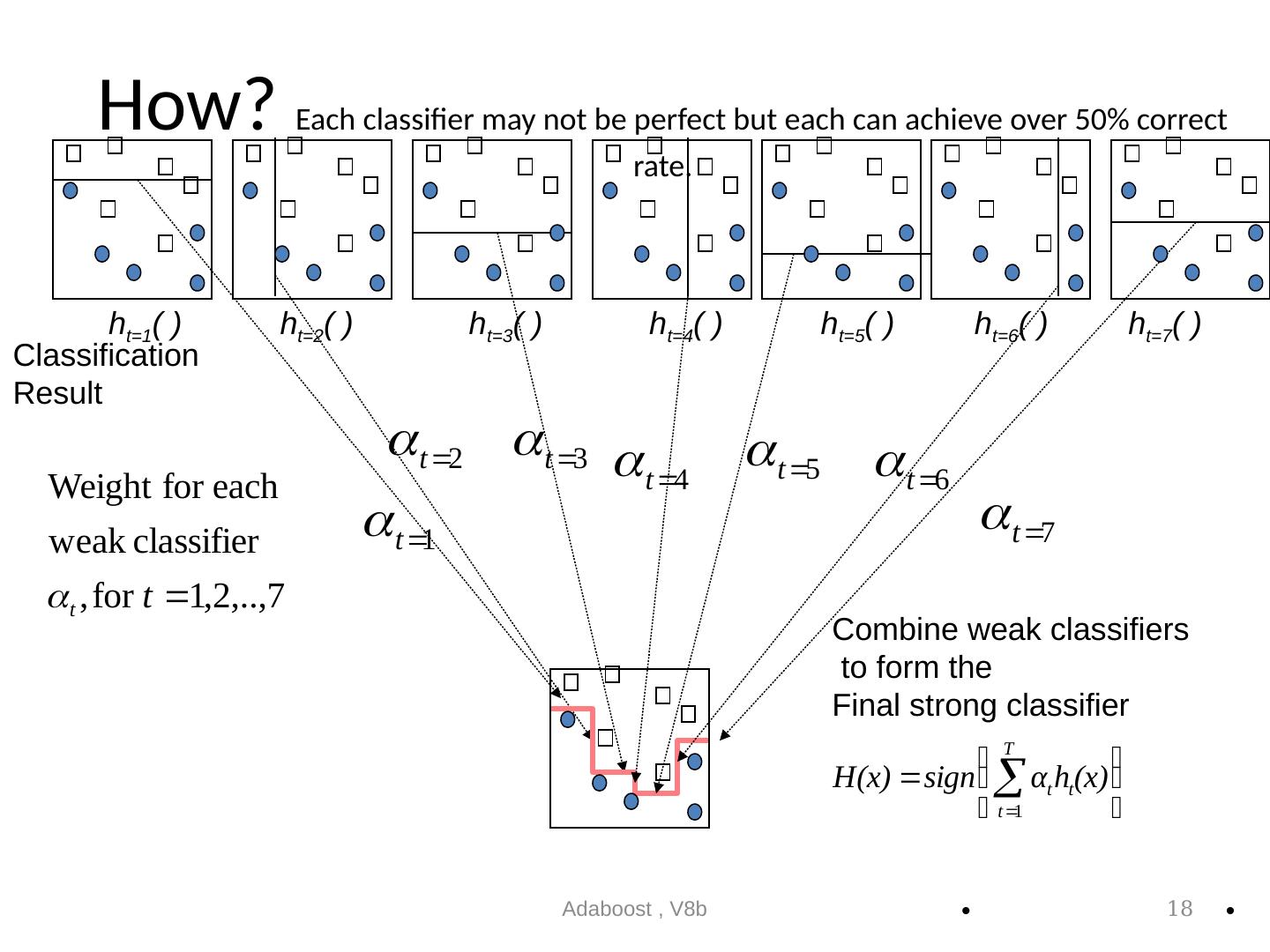
18 .How? Each classifier may not be perfect but each can achieve over 50% correct rate. Adaboost , V8b 18 Classification Result Combine weak classifiers to form the Final strong classifier h t = 1 ( ) h t =2 ( ) h t =3 ( ) h t =4 ( ) h t =5 ( ) h t =6 ( ) h t = 7 ( )

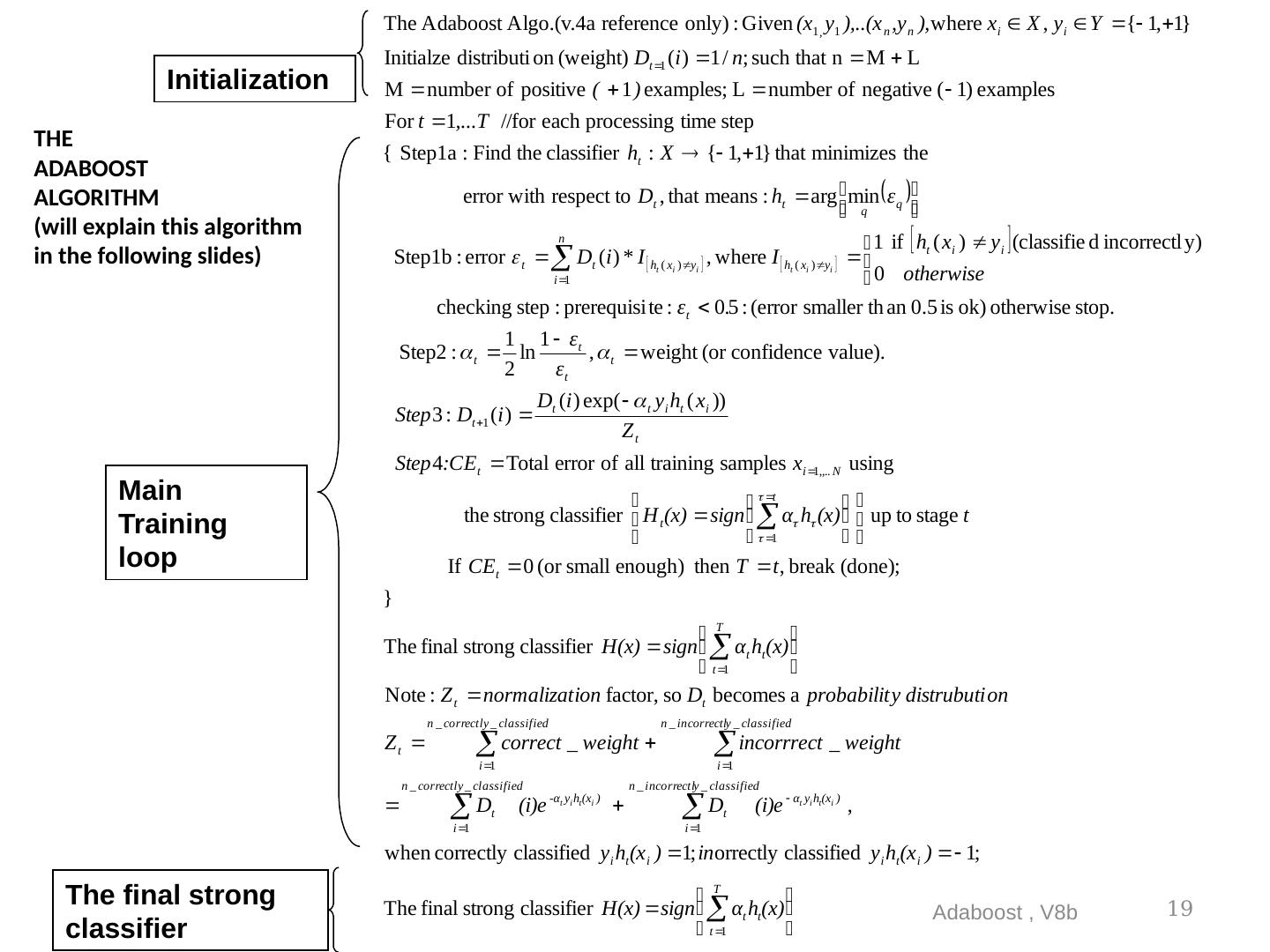
19 .THE ADABOOST ALGORITHM (will explain this algorithm in the following slides) Adaboost , V8b 19 Initialization Main Training loop The final strong classifier

20 .Initialization Adaboost , V8b 20

21 .D t (i) =weight D t (i) = probability distribution of the i-th training sample at time t . i=1,2…n. It shows how much you trust this sample. At t=1 , all samples are the same with equal weight. D t=1 (all i) are the same At t > 1 , D t>1 (i) will be modified, we will see later. Adaboost , V8b 21

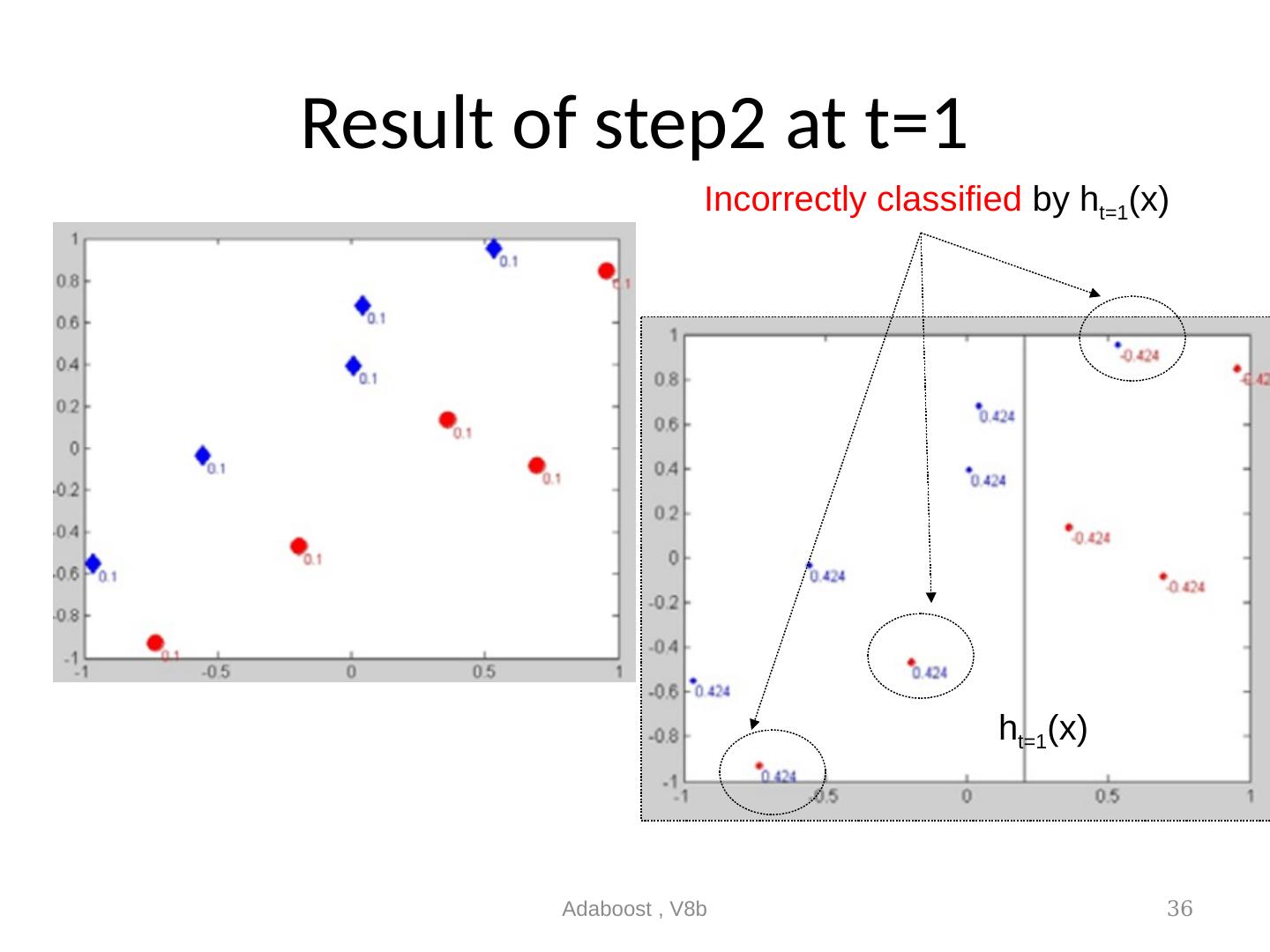
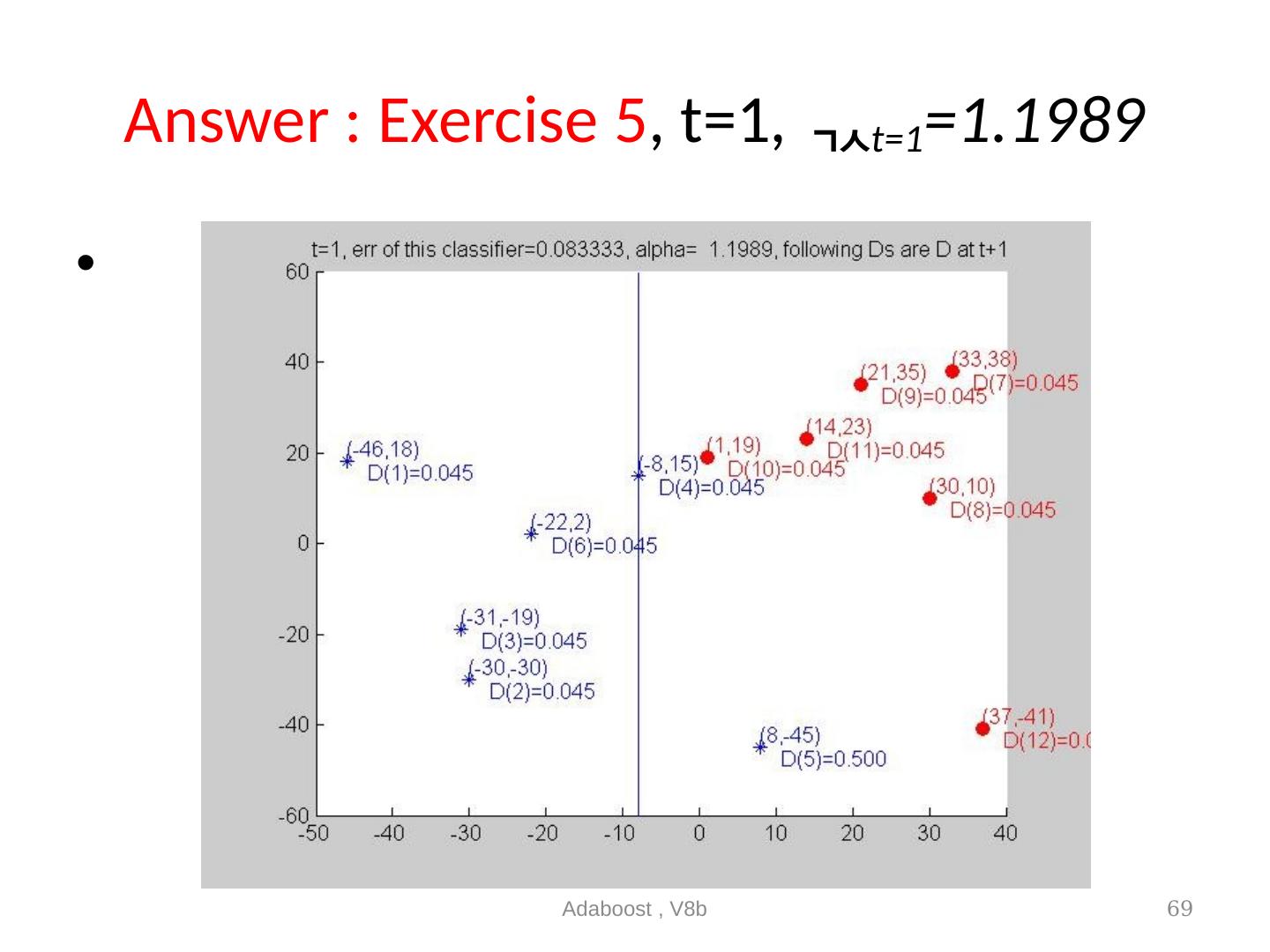
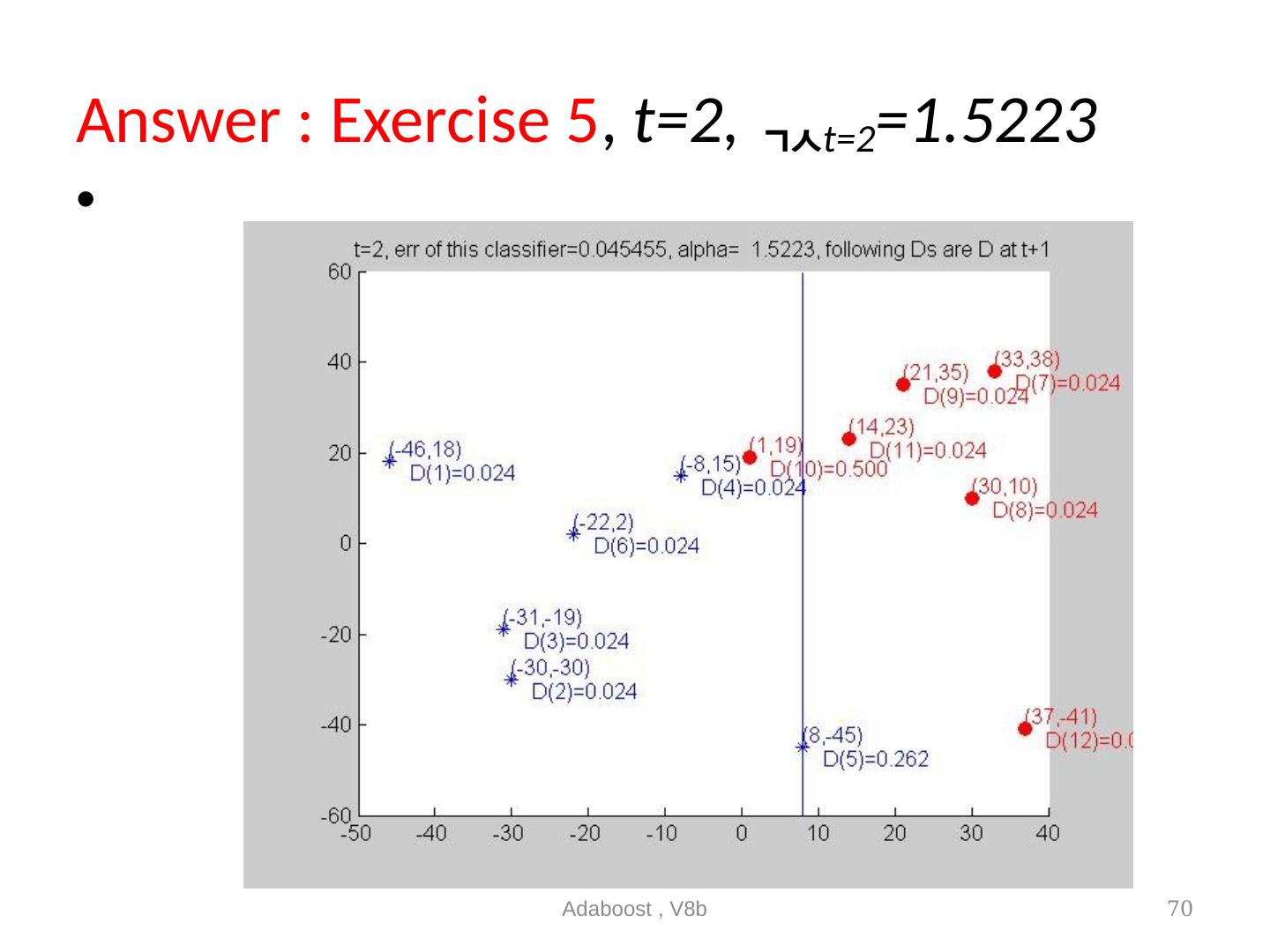
22 .Main loop (step1,2,3) t is the index for the weak classifier at stage t , T is the number of weak classifiers needed Adaboost , V8b 22 Z t = normalization factor it will be discussed later

23 .Main Loop Step 4 (updated) Step 4 in English: If all training samples x i =1,..,all are correctly classified by H(),then stop the training Adaboost , V8b 23

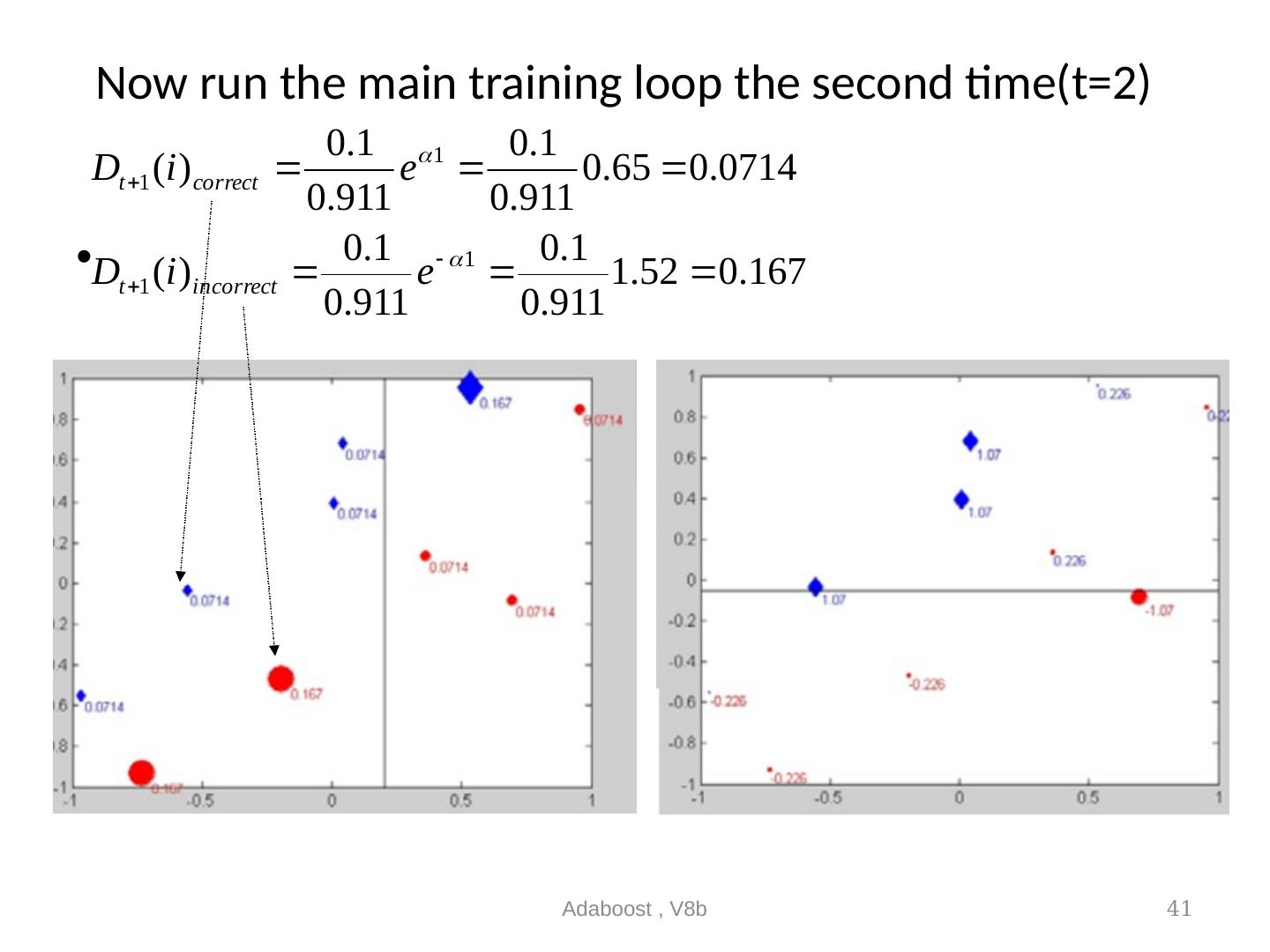
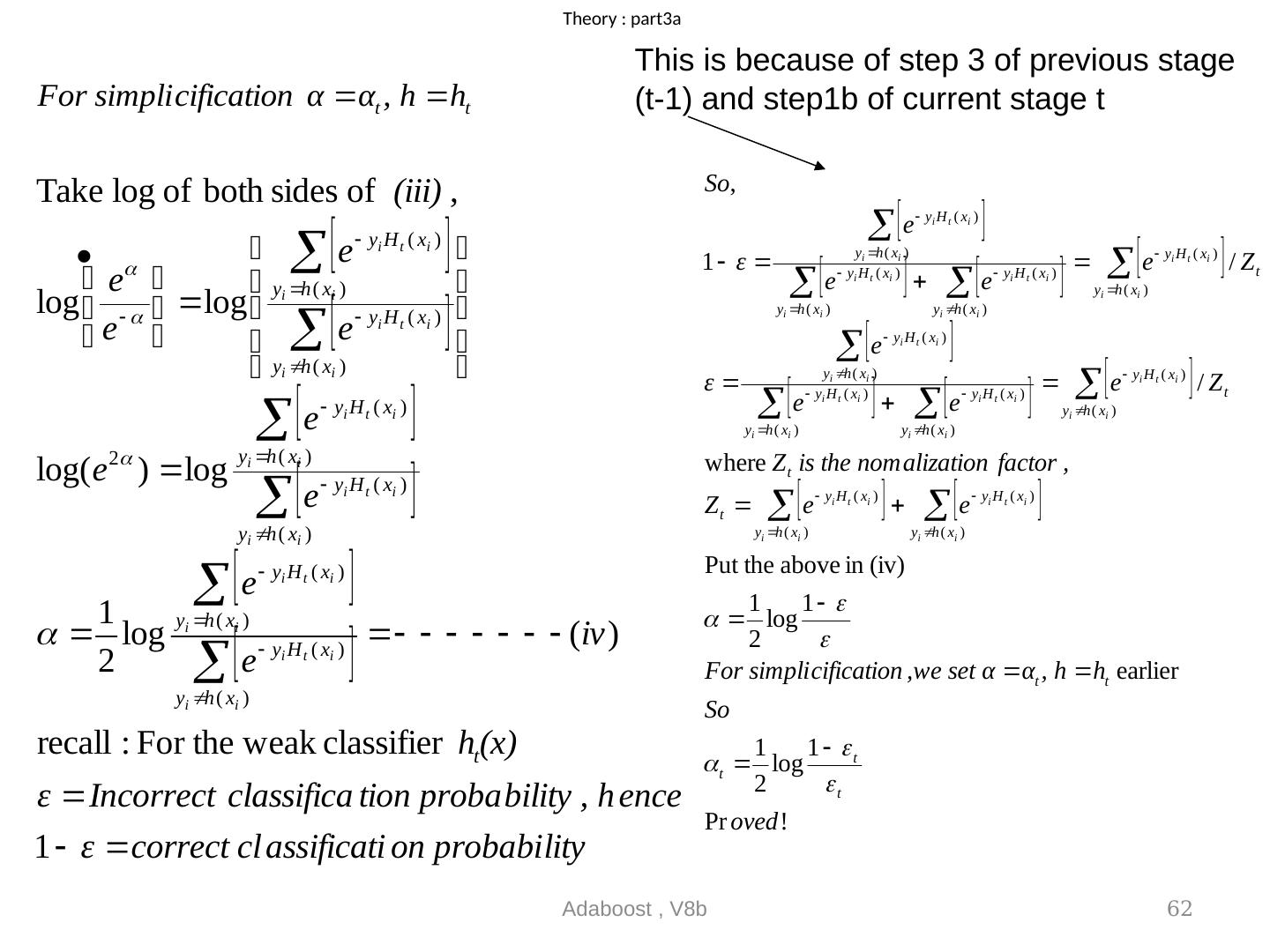
24 .Note: To find Normalization factor Z t in step3 Adaboost , V8b 24 AdaBoost chooses this weight_update function deliberately Because the idea is, when a training sample is correctly classified, weight decreases when a training sample is incorrectly classified, weight increases

25 .An example to show how Adaboost works Training, Present ten samples to the system :[xi={ui,vi},yi={’+’ or ‘-’}] 5 +ve (blue, diamond) samples 5 –ve (red, circle) samples Train up the classification system. Detection example: Give an input xj=(1.5,3.4) The system will tell you it is ‘+’ or ‘-’. E.g. Face or non-face. Example: You may treat u =skills, v =height Classification task: suitability to play in the basket ball team. Adaboost , V8b 25 [xi={-0.48,0},yi=’+’] [xi={-0.2,-0.5},yi=’+’] u-axis v-axis

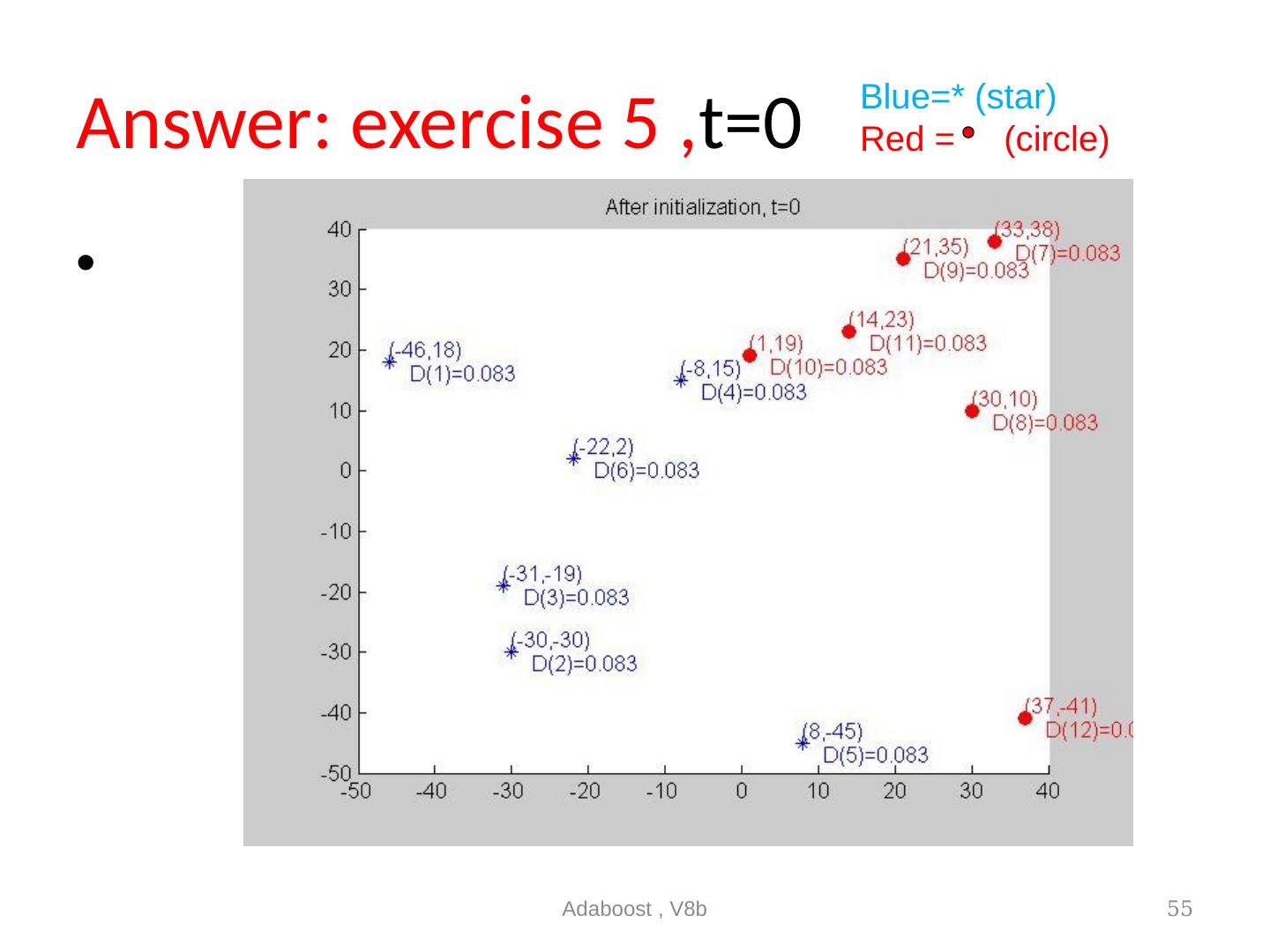
26 .Initialization M=5 +ve (blue, diamond) samples L=5 –ve (red, circle) samples n=M+L=10 (usually make M  N) Initialize weight D (t=1) (i)= 1/10 for all i=1,2,..,10, So, D (1) (1)=0.1, D (1) (2)=0.1,……, D (1) (10)=0.1 Adaboost , V8b 26

27 .Main training loop Step 1a, 1b Adaboost , V8b 27

28 .Select h( ): For simplicity in implementation we use the axis-parallel weak classifier Adaboost , V8b 28 h a (x) h b (x) u 0 v 0

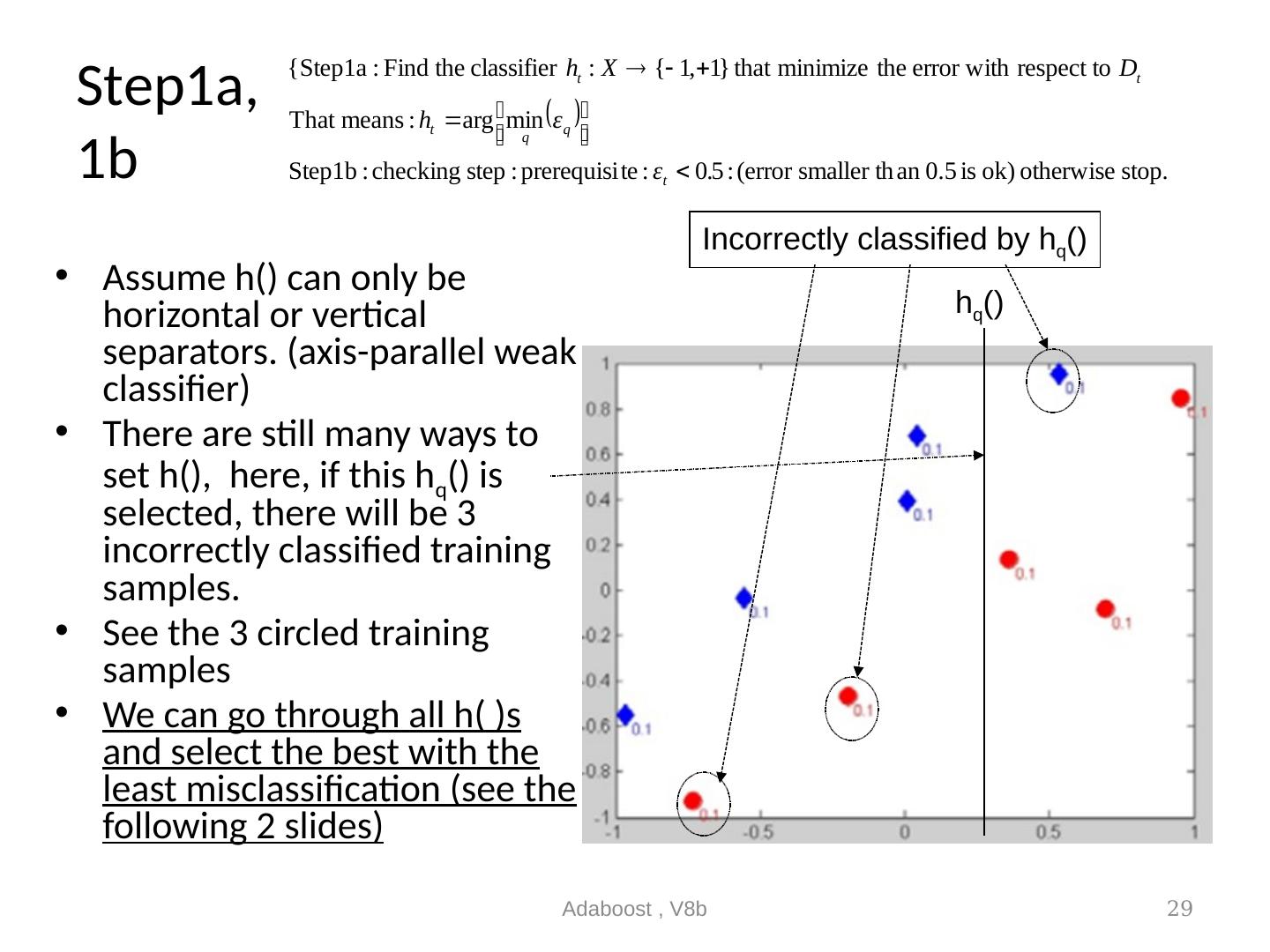
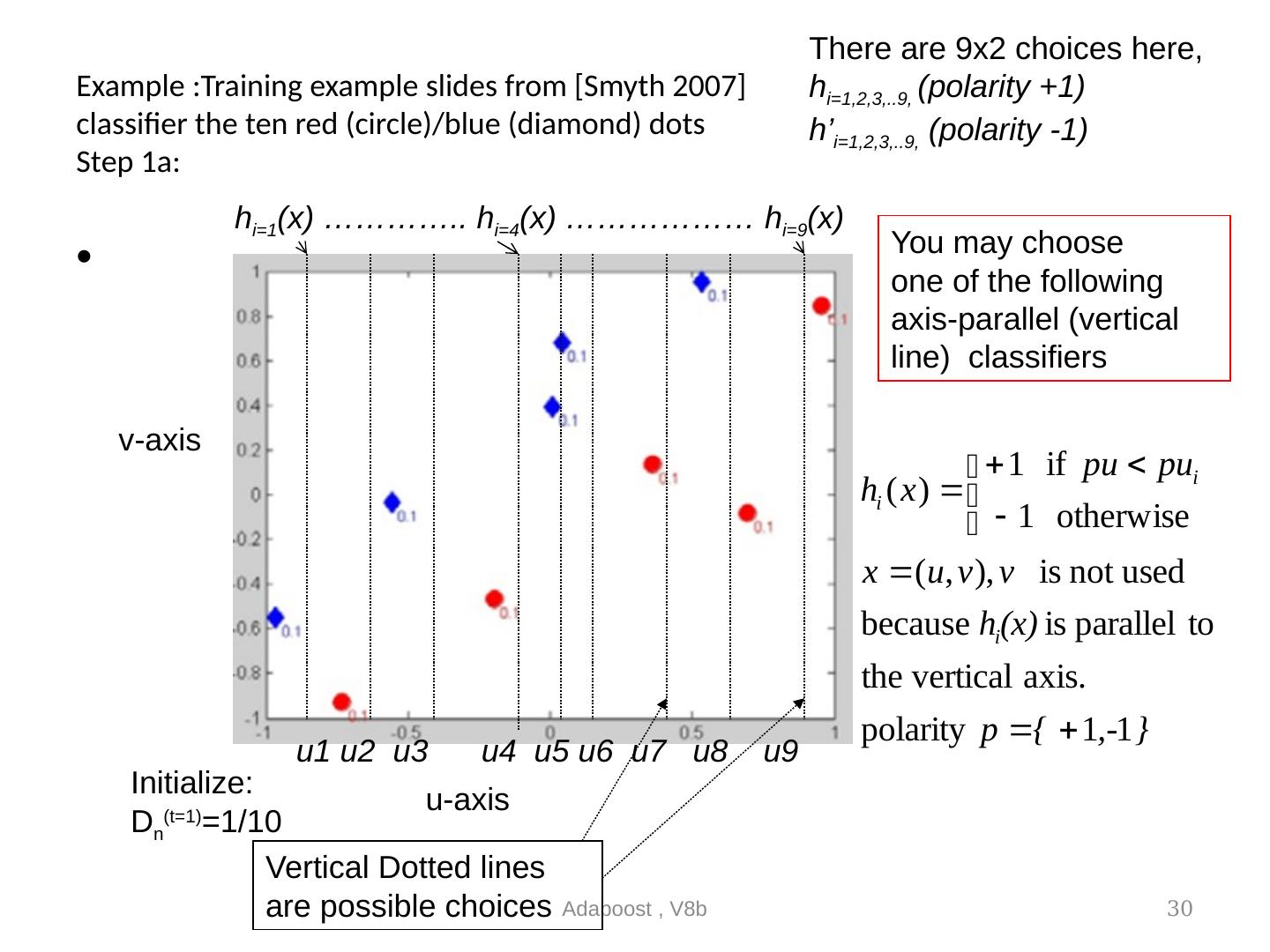
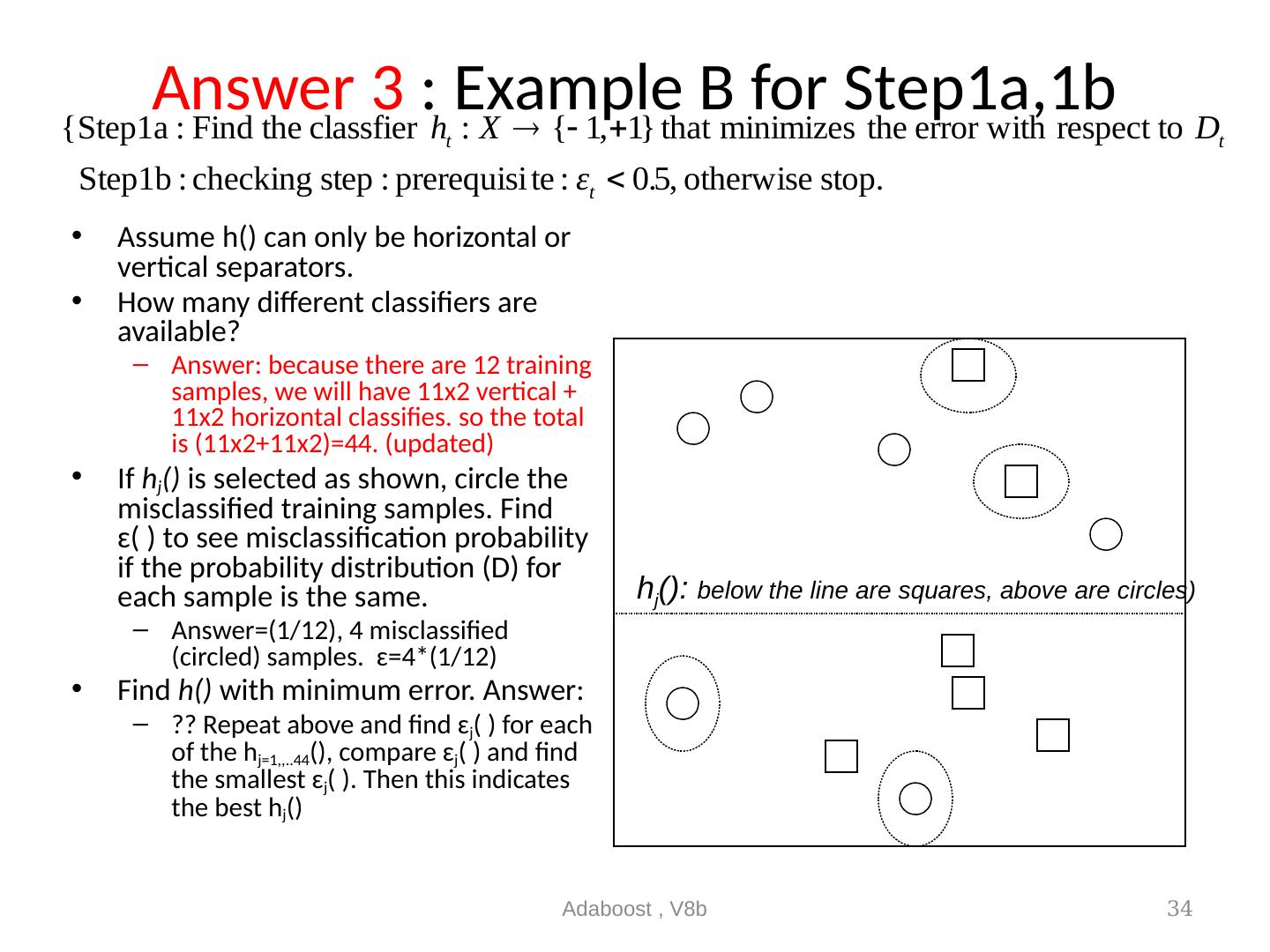
29 .Step1a, 1b Assume h() can only be horizontal or vertical separators. (axis-parallel weak classifier) There are still many ways to set h(), here, if this h q () is selected, there will be 3 incorrectly classified training samples. See the 3 circled training samples We can go through all h( )s and select the best with the least misclassification (see the following 2 slides) Adaboost , V8b 29 Incorrectly classified by h q () h q ()