02_ Preprocessing of audio signals in time and frequency domain

1 .Ch. 2 : Preprocessing of audio signals in time and frequency domain Time framing Frequency model Fourier transform Spectrogram Preprocessing Ch2 , v8c 1

2 . Revision: Raw data and PCM Human listening range 20Hz  20K Hz CD Hi-Fi quality music: 44.1KHz (sampling) 16bit People can understand human speech sampled at 5KHz or less, e.g. Telephone quality speech can be sampled at 8KHz using 8-bit data. Speech recognition systems normally use: 10~16KHz,12~16 bit. Preprocessing Ch2 , v8c 2

3 .Concept: Human perceives data in blocks We see 24 still pictures in one second, then we can build up the motion perception in our brain. It is likewise for speech Preprocessing Ch2 , v8c 3 Source: http://antoniopo.files.wordpress.com/2011/03/eadweard_muybridge_horse.jpg?w=733&h=538

4 .Time framing Since our ear cannot response to very fast change of speech data content, we normally cut the speech data into frames before analysis . (similar to watch fast changing still pictures to perceive motion ) Frame size is 10~30ms (1ms=10 -3 seconds) Frames can be overlapped, normally the overlapping region ranges from 0 to 75% of the frame size . Time framing Video demo: https://youtu.be/lOu-c2UHU00 Preprocessing Ch2 , v8c 4

5 .Frame blocking and Windowing To choose the frame size (N samples )and adjacent frames separated by m samples. I.e.. a 16KHz sampling signal, a 10ms window has N=160 samples, ( non-overlap samples ) m=40 samples Preprocessing Ch2 , v8c 5 l =1 (first window), length = N m N N l =2 (second window), length = N n s n time

6 .Tutorial for frame blocking A signal is sampled at 12KHz, the frame size is chosen to be 20ms and adjacent frames are separated by 5ms. Calculate N and m and draw the frame blocking diagram. (ans: N=240, m=60.) Repeat above when adjacent frames do not overlap. (ans: N=240, m=240.) Preprocessing Ch2 , v8c 6

7 .Class exercise 2.1 For a 22-KHz/16 bit sampling speech wave, frame size is 15 ms and frame overlapping period is 40 % of the frame size. Draw the frame blocking diagram. Preprocessing Ch2 , v8c 7

8 .The frequency model For a frame we can calculate its frequency content by Fourier Transform (FT) Computationally, you may use Discrete-FT (DFT) or Fast-FT (FFT) algorithms. FFT is popular because it is more efficient. FFT algorithms can be found in most numerical method textbooks /web pages . E.g. http://en.wikipedia.org/wiki/Fast_Fourier_transform Preprocessing Ch2 , v8c 8

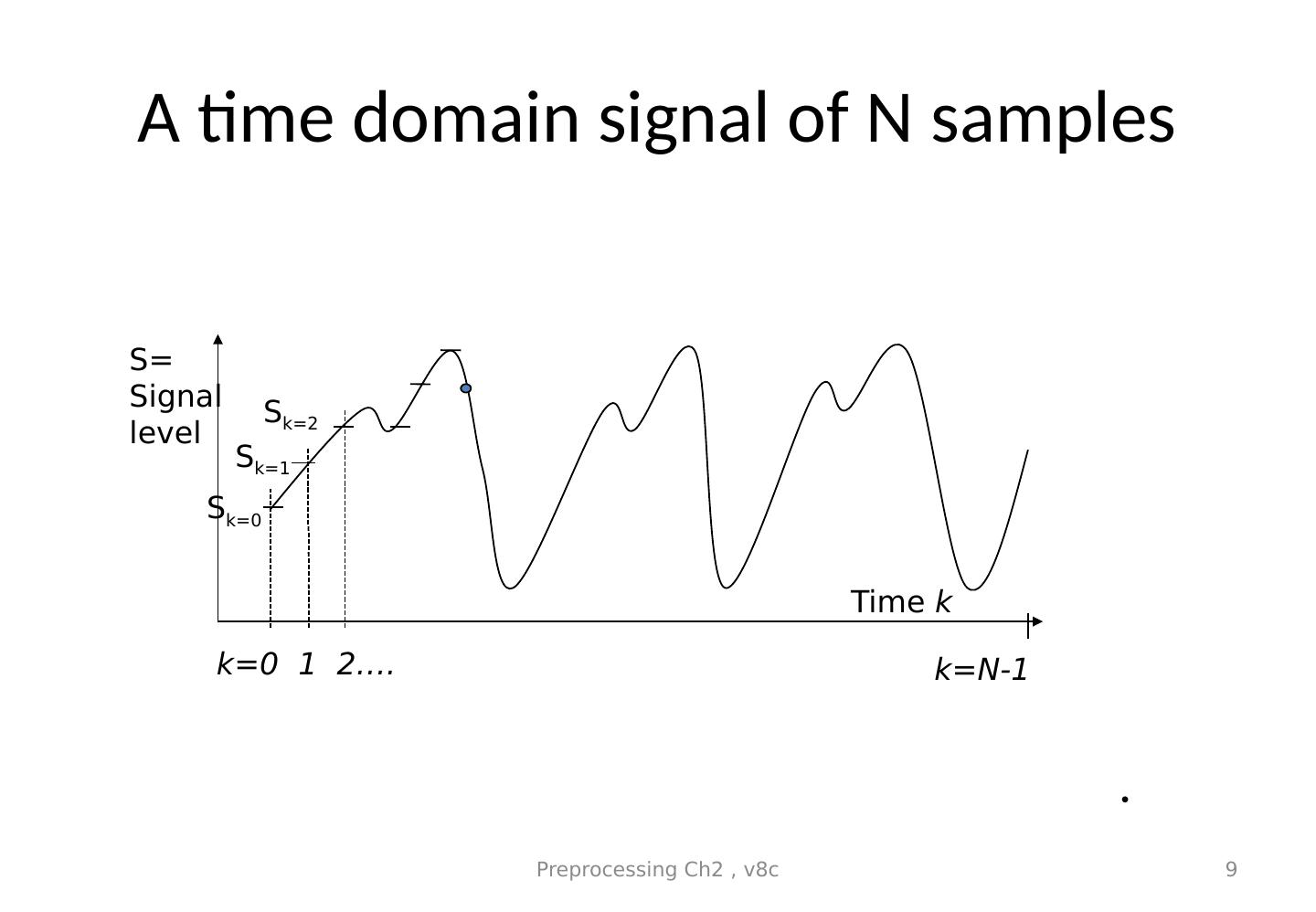
9 .A time domain signal of N samples 9 S k =0 S k =2 S= Signal level Time k S k =1 k=0 1 2…. k=N-1 Preprocessing Ch2 , v8c

10 .The F ourier T ransform FT method (see appendix of why m  N/2) Forward Transform (FT) of N sample data points Preprocessing Ch2 , v8c 10 Demo Matlab code: demo_dft_tutorial.rar

11 .Fourier Transform Preprocessing Ch2 , v8c 11 Called spectral envelop S 0 ,S 1 ,S 2 ,S 3. … S N-1 Time Signal voltage/ pressure level Fourier Transform freq. (m) single freq.. Power= | X m |= (real 2 +imginary 2 ) Demo Matlab code: demo_dft_tutorial.rar Demo Video

12 .Example [s0,s1,s2,…]=[1 ,3 ,4,…], N=128, m=0,…,64 X m =0 =1*e -j(2*pi*0*0/128 ) +3*e -j(2*pi*1*0/128) + 4*e -j(2*pi*2*0/128) +.. X m =1 =1*e -j(2*pi*0*1/128 ) + 3*e -j(2*pi*1*1/128 ) + 4*e -j(2*pi*2*1/128) +.. X m =2 =1*e -j(2*pi*0*2/128 ) + 3*e -j(2*pi*1*2/128 ) + 4*e -j(2*pi*2*2/128 ) +.. Preprocessing Ch2 , v8c 12

13 .Examples of FT (P ure wave vs. speech wave) Preprocessing Ch2 , v8c 13 time(k) pure cosine has one frequency band single freq.. | X m | s k complex speech wave has many different frequency bands s k time(k) FT freq.. (m) freq. (m) single freq.. | X m | Spectral envelop http:// math.stackexchange.com/questions/1002/fourier-transform-for-dummies DFT and Inverse: DFT https :// www.mathworks.com/matlabcentral/fileexchange/41228-dft-and-idft/content/Untitled3.m

14 .Discrete Fourier transform DFT and Inverse Discrete Fourier transform IDFT Preprocessing Ch2 , v8c 14 https:// en.wikipedia.org/wiki/Discrete_Fourier_transform Matlab code: https :// www.mathworks.com/matlabcentral/fileexchange/41228-dft-and-idft/content/Untitled3.m

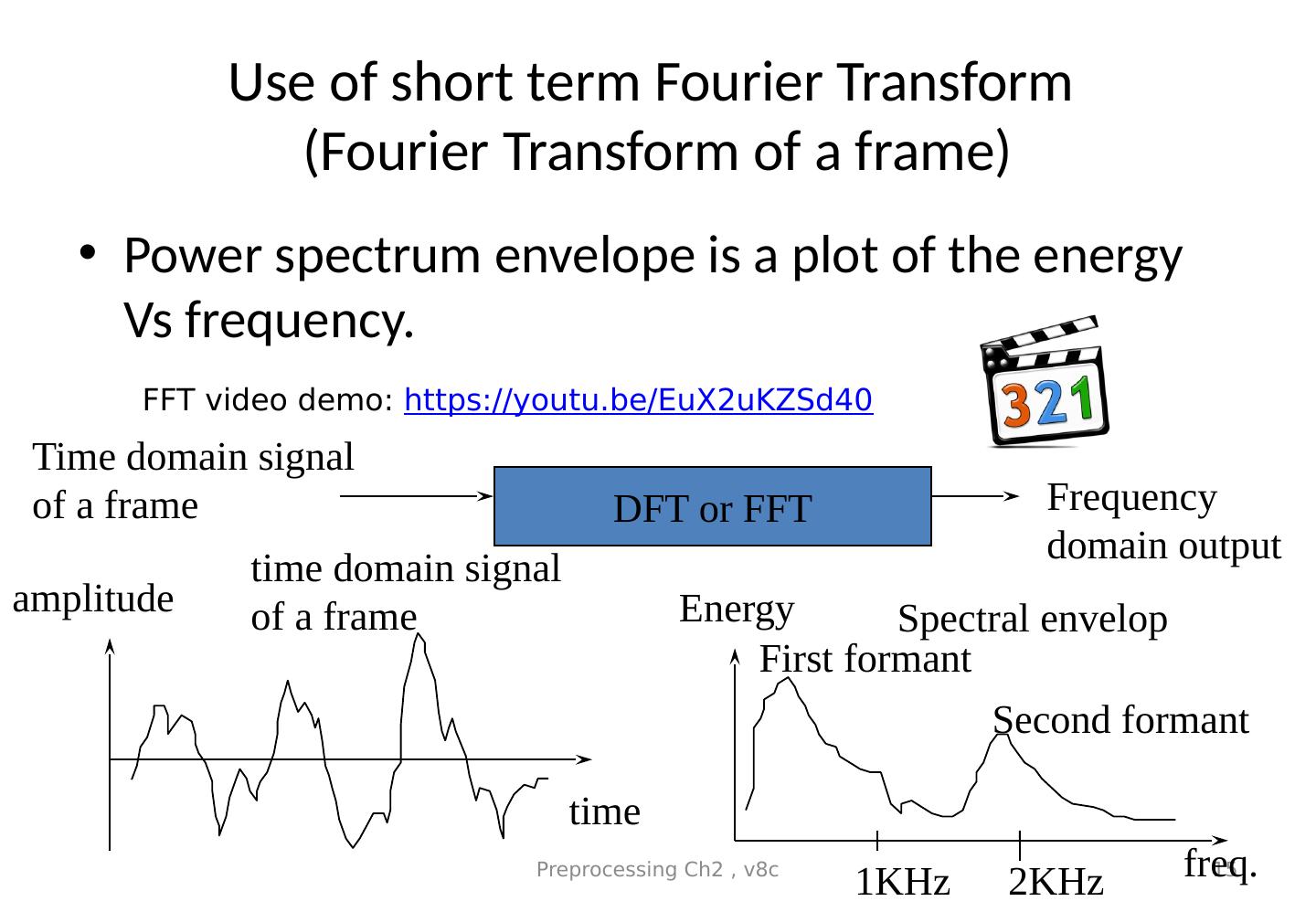
15 .Use of short term Fourier Transform ( Fourier Transform of a frame) Power spectrum envelope is a plot of the energy Vs frequency. Preprocessing Ch2 , v8c 15 DFT or FFT Time domain signal of a frame Frequency domain output amplitude time freq.. Energy Spectral envelop time domain signal of a frame 1 KHz 2 KHz First formant Second formant FFT video demo: https://youtu.be/EuX2uKZSd40

16 .Class exercise 2.2: Fourier Transform Write pseudo code (or a C /matlab/octave program segment but not using a library function ) to transform a signal in an array . Int s[256] into the frequency domain in float X[128+1] (real part result) and float IX[128+1] (imaginary result). How to generate a spectrogram? Preprocessing Ch2 , v8c 16

17 .The spectrogram: to see the spectral envelope as time moves forward It is a visualization method (tool) to look at the frequency content of a signal. Parameter setting: (1)Window size = N =(e.g. 512)= number of time samples for each Fourier Transform processing. (2) non-overlapping sample size D (e.g. 128). (3) frame index is j . t is an integer, initialize t =0, j=0. X-axis = time, Y-axis = freq. Step1: FT samples S t+j *D to S t+512+j*D Step2: plot FT result ( freq v.s . energy) spectral envelope vertically using different gray scale. Step3: j=j+1 Repeat Step1,2,3 until j * D+t+512 >length of the input signal. Preprocessing Ch2 , v8c 17

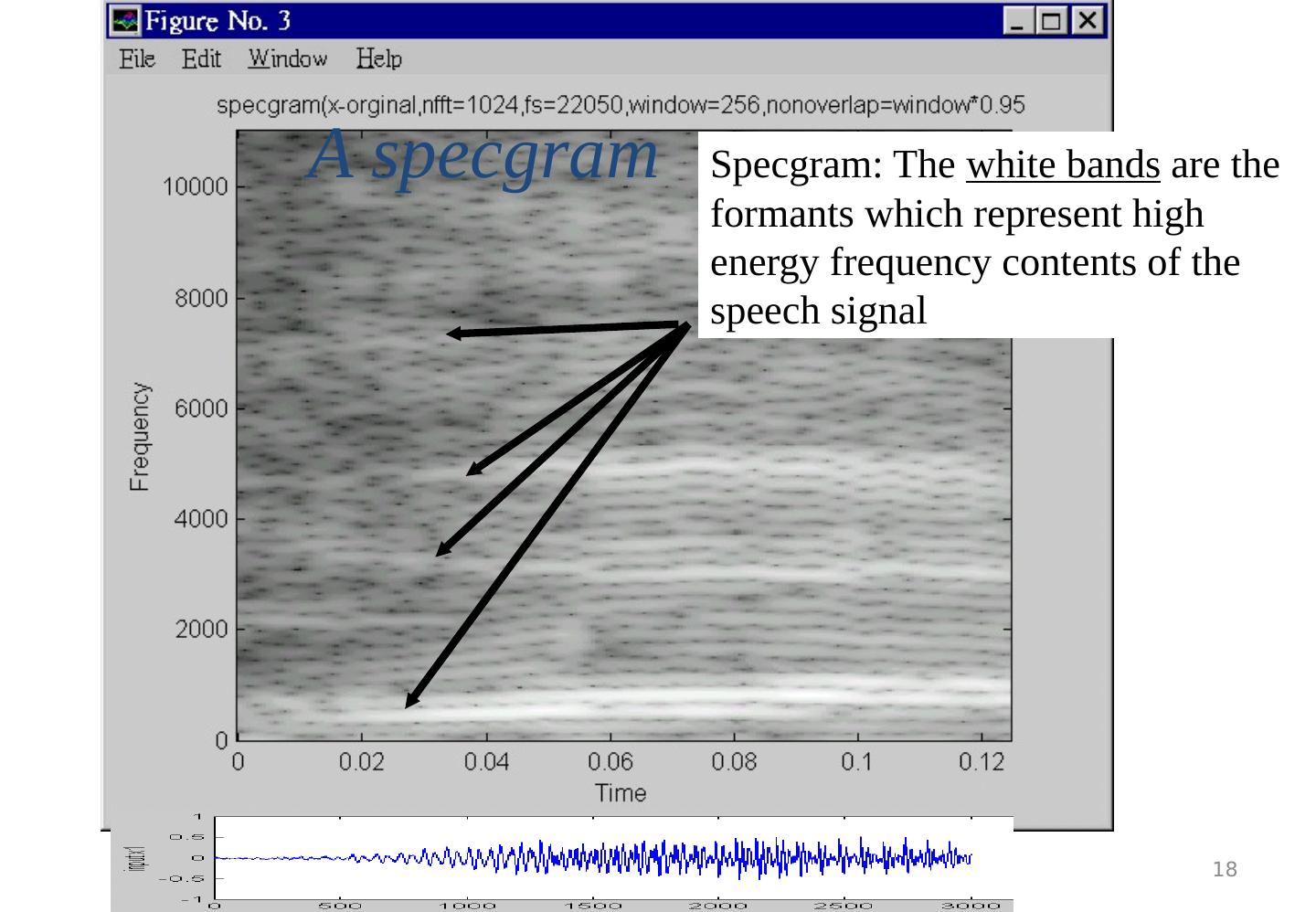
18 .Preprocessing Ch2 , v8c 18 A specgram Specgram: The white bands are the formants which represent high energy frequency contents of the speech signal

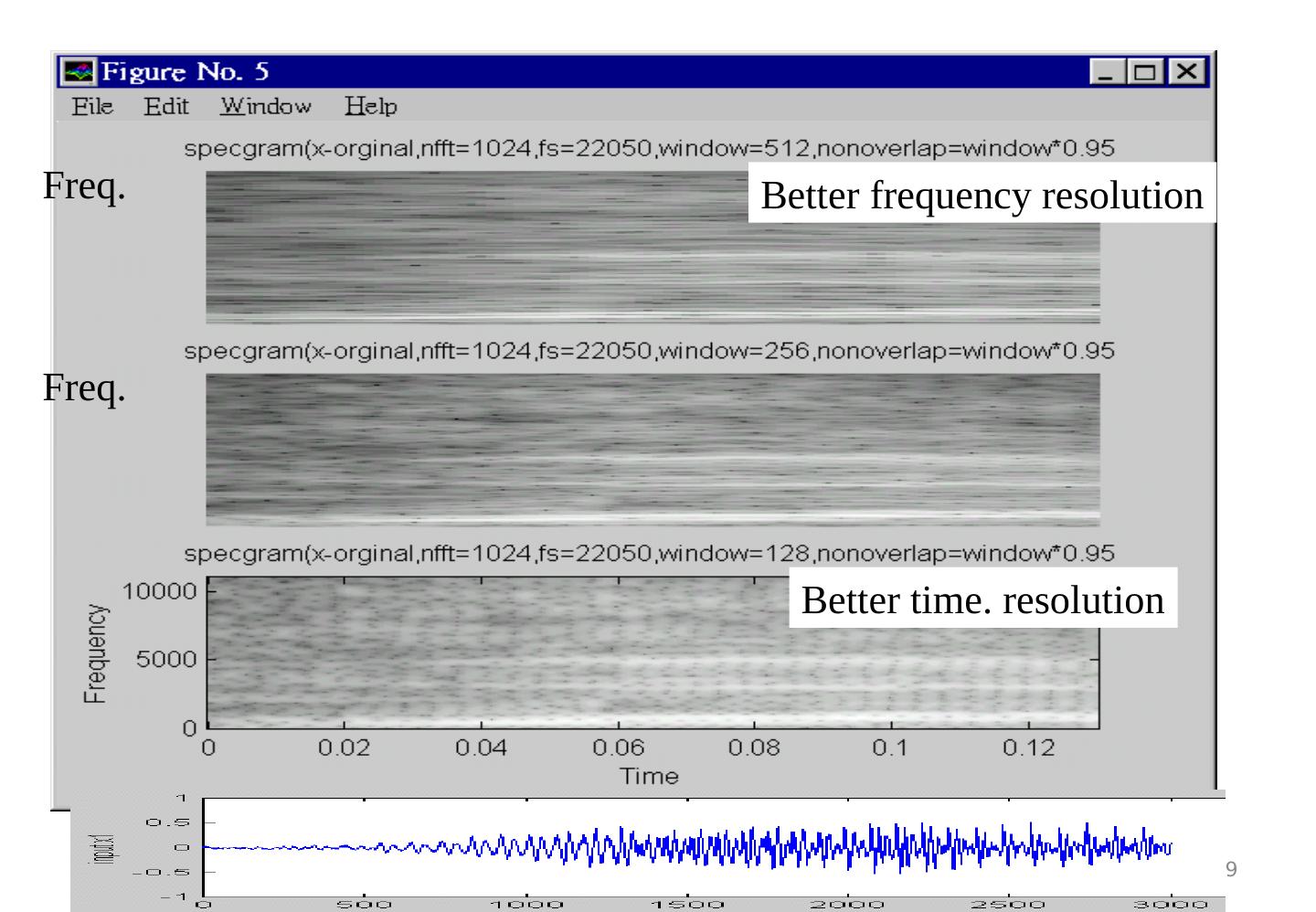
19 .Preprocessing Ch2 , v8c 19 Better time. resolution Better frequency resolution Freq. Freq.

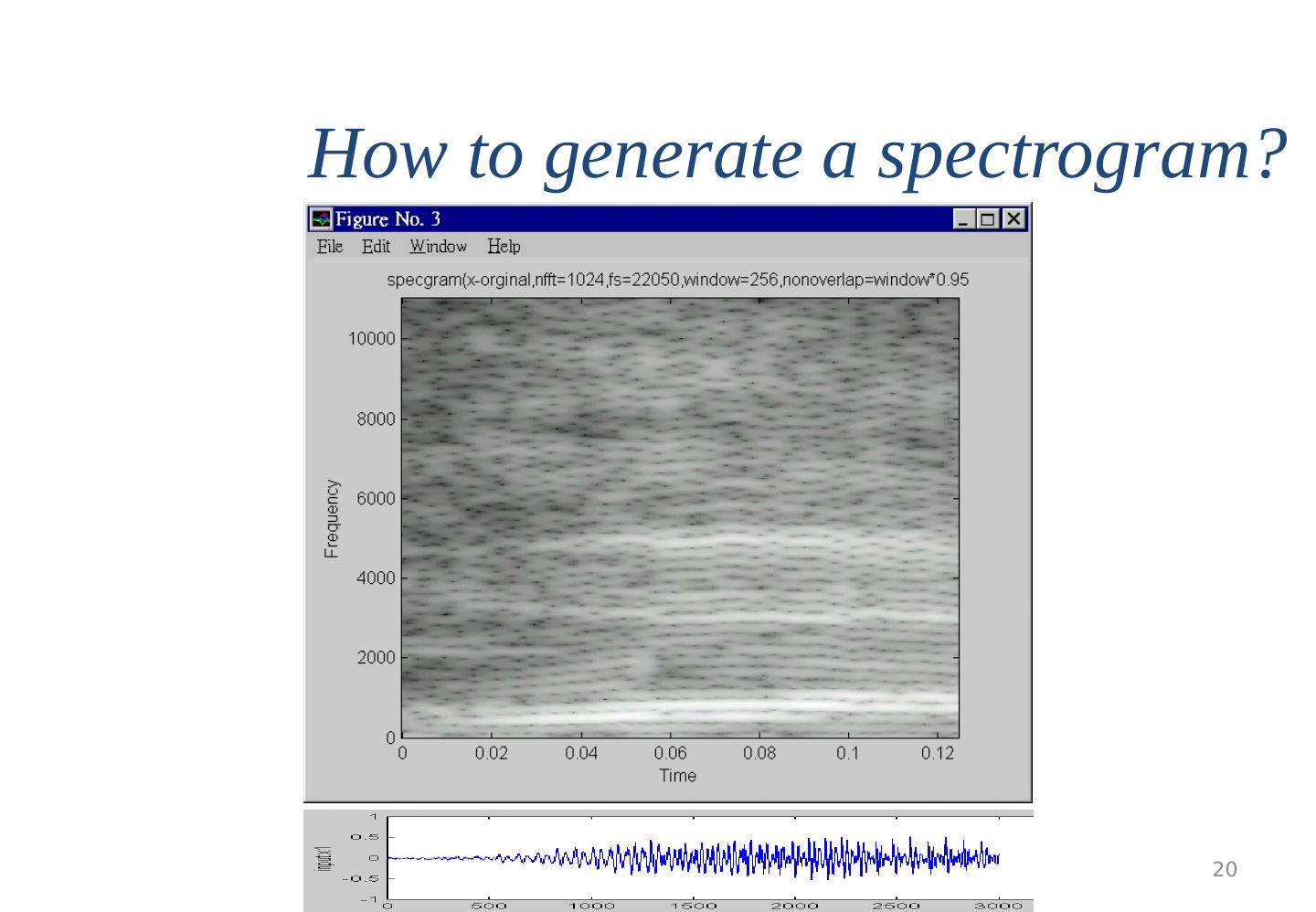
20 .Preprocessing Ch2 , v8c 20 How to generate a spectrogram?

21 .Preprocessing Ch2 , v8c 21 Procedures to generate a spectrogram (Specgram1) Window=256-> each frame has 256 samples Sampling is fs =22050, so maximum frequency is 22050/2=11025 Hz Nonverlap =window*0.95=256*.95=243 , overlap is small (overlapping =256-243=13 samples) For each frame (256 samples) Find the magnitude of Fourier X_magnitude(m), m=0,1,2, 128 Plot X_magnitude(m)= Vertically, -m is the vertical axis -|X(m)|=X_magnitude(m) is represented by intensity Repeat above for all frames q=1,2,..Q |X(0)| |X(i)| |X(128)| Frame q=1 Frame q=Q frame q=2

22 .Class exercise 2.3: In specgram1 Calculate the first sample location and last sample location of the frames q=3 and 7. Note: N=256, m=243 Answer: q=1, frame starts at sample index =? q=1, frame ends at sample index =? q=2, frame starts at sample index =? q=2, frame ends at sample index =? q=3, frame starts at sample index =? q=3, frame ends at sample index =? q=7, frame starts at sample index =? q=7, frame ends at sample index =? Preprocessing Ch2 , v8c 22

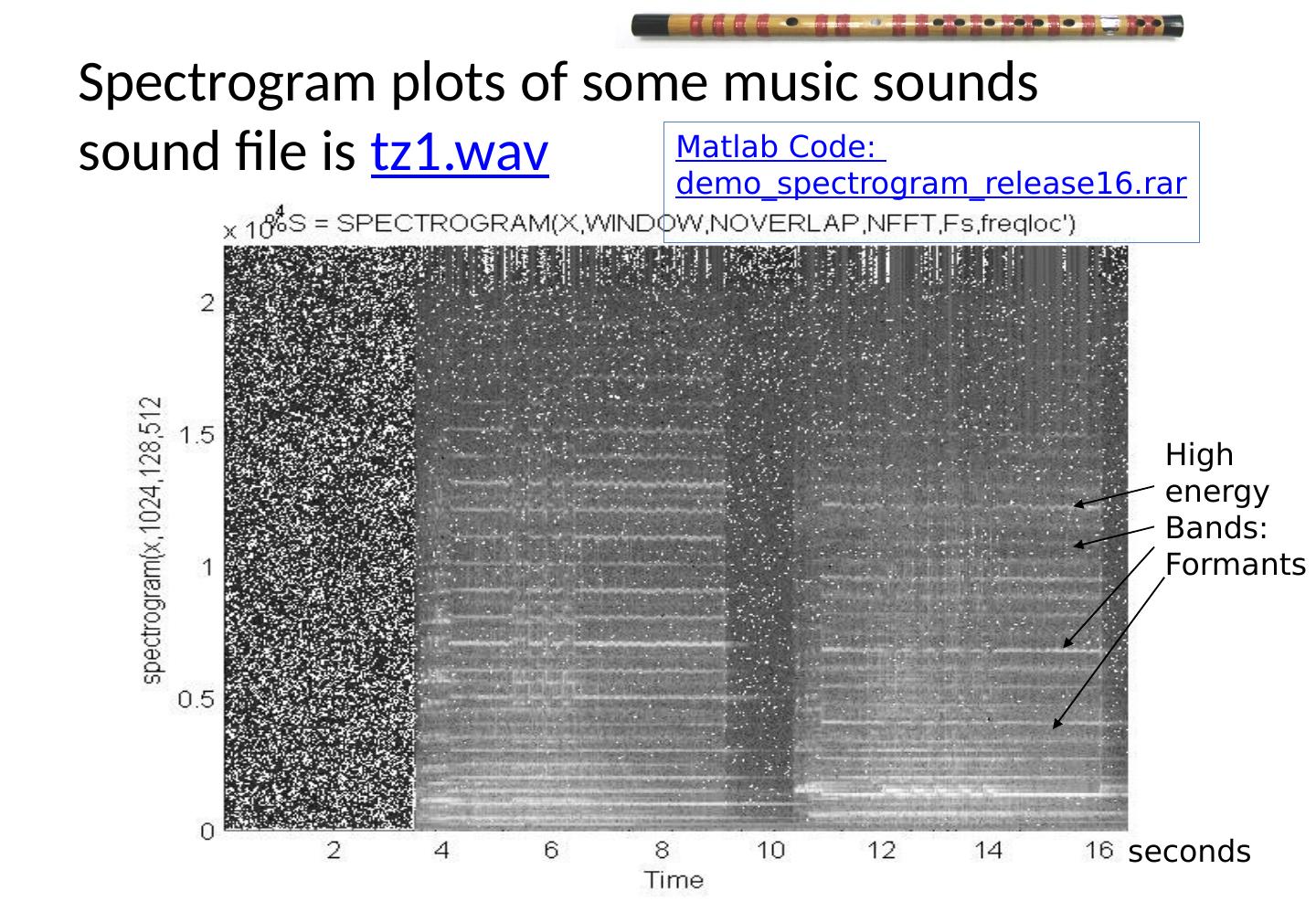
23 .Spectrogram plots of some music sounds sound file is tz1.wav Preprocessing Ch2 , v8c 23 High energy Bands: Formants seconds Matlab Code: demo_spectrogram_release16.rar

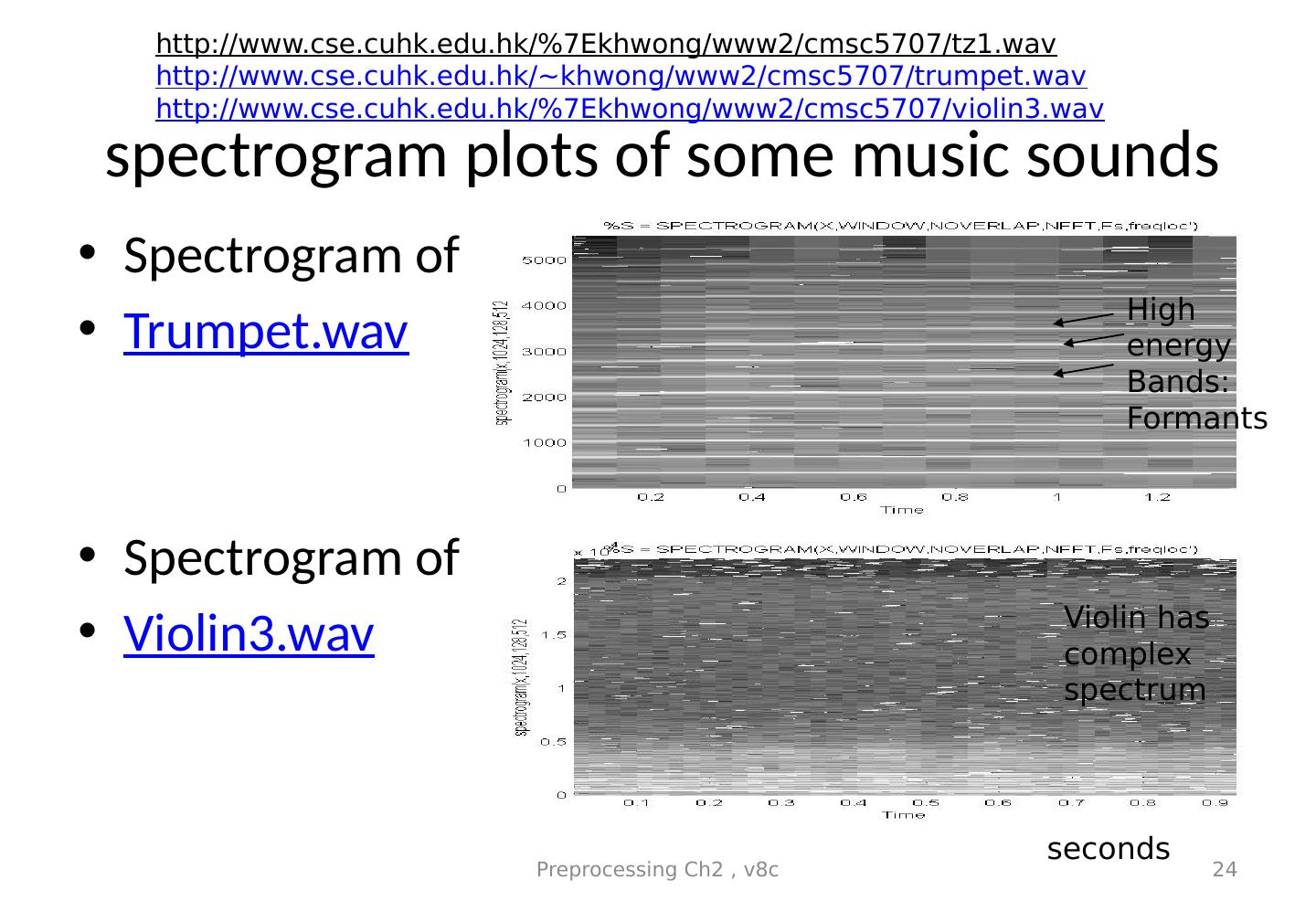
24 .spectrogram plots of some music sounds Spectrogram of Trumpet.wav Spectrogram of Violin3.wav Preprocessing Ch2 , v8c 24 High energy Bands: Formants Violin has complex spectrum seconds http://www.cse.cuhk.edu.hk/%7Ekhwong/www2/cmsc5707/tz1.wav http://www.cse.cuhk.edu.hk/~khwong/www2/cmsc5707/trumpet.wav http://www.cse.cuhk.edu.hk/%7Ekhwong/www2/cmsc5707/v iolin3.wav

25 .Exercise 2.4 Write the procedures for generating a spectrogram from a source signal X. Preprocessing Ch2 , v8c 25

26 .Summary Studied Basic digital audio recording systems Speech recognition system applications and classifications Fourier analysis and spectrogram Preprocessing Ch2 , v8c 26

27 .Appendix Preprocessing Ch2 , v8c 27

28 .Answer: Class exercise 2.1 For a 22-KHz/16 bit sampling speech wave, frame size is 15 ms and frame overlapping period is 40 % of the frame size. Draw the frame block diagram. Answer: Number of samples in one frame (N)= 15 ms / (1/22k) = 15*(10^-3) /(1/( 22000 ))= 330 Overlapping samples = 132, m=N-132=198. Overlapping time = 132 * (1/22k)= 132 * ( 1/22000) =6ms ; Time in one frame= 330* (1/22k )= 330* ( 1/22000)=15ms . Preprocessing Ch2 , v8c 28 l =1 (first window), length = N m N N l =2 (second window), length = N n s n time

29 .Answer Class exercise 2.2: Fourier Transform For (m=0;m<=N/2;m++) { tmp_real =0; tmp_img =0; For(k=0;k< = N-1;k++) { tmp_real = tmp_real+S k * cos (2*pi*k*m/N); tmp_img = tmp_img-S k *sin(2*pi*k*m/N); } X_real (m)= tmp_real ; X_img (m)= tmp_img ; } From N input data S k =0,1,2,3..N-1 , there will be 2*(N+1) data generated, i.e. X_real (m), X_img (m), m=0,1,2,3..N/2 are generated. E.g. S k =S 0 ,S 1 ,..,S 511  X _real 0 , X _real 1 ,.., X _real 256, X _imgl 0 , X _img 1 ,.., X _img 256, Note that X_magnitude (m)= sqrt [ X_real (m) 2 + X_img (m) 2 ] Preprocessing Ch2 , v8c 29 http://en.wikipedia.org/wiki/List_of_trigonometric_identities