22-Termination Detection

1 .CSC2/458 Parallel and Distributed Systems Termination Detection Sreepathi Pai April 12, 2018 URCS 

2 .Outline Termination Detection Ring termination (Dijkstra et al.) Misra’s Algorithm 

3 .Outline Termination Detection Ring termination (Dijkstra et al.) Misra’s Algorithm 

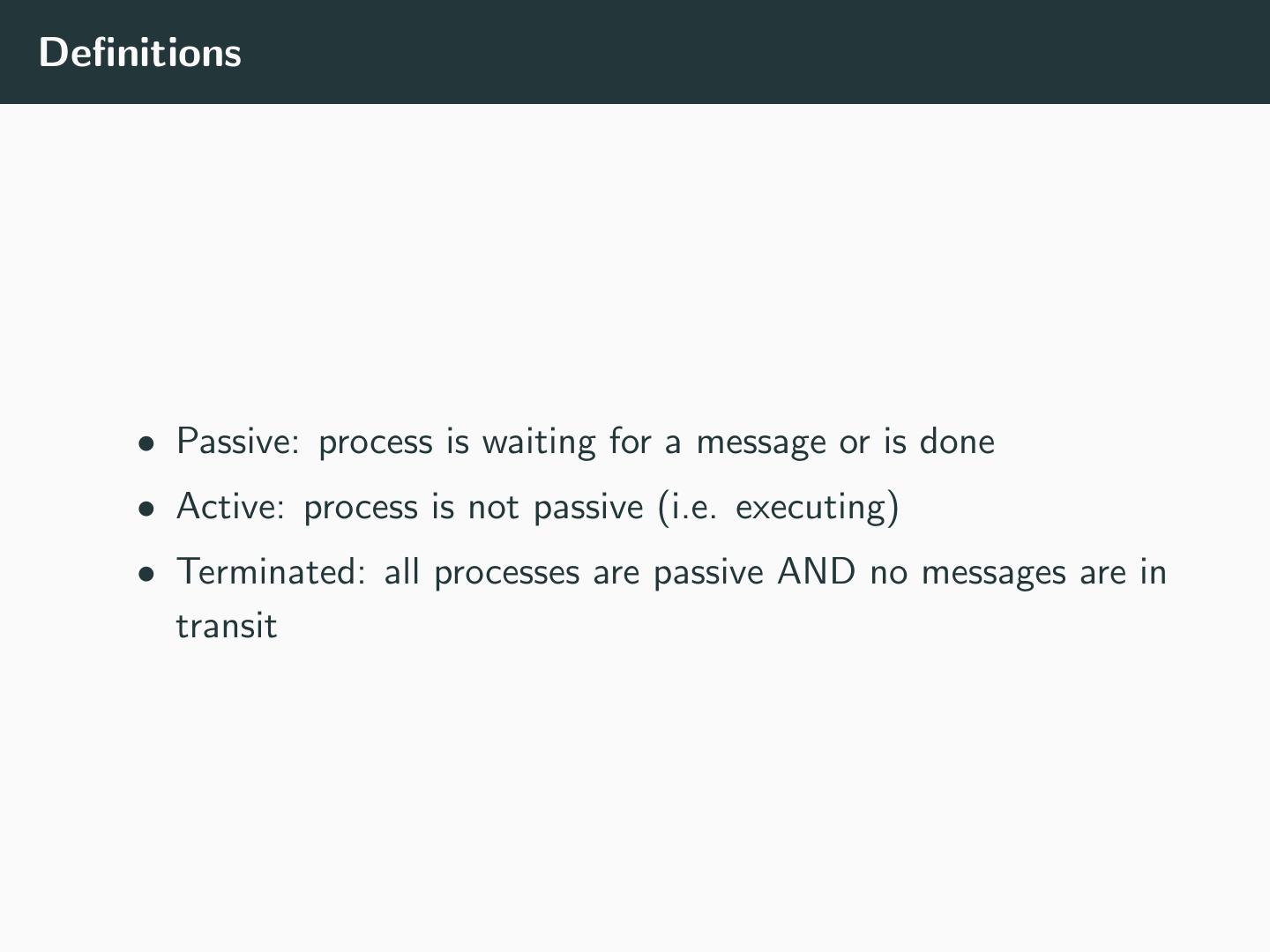
4 .Definitions • Passive: process is waiting for a message or is done • Active: process is not passive (i.e. executing) • Terminated: all processes are passive AND no messages are in transit 

5 .Global Termination Detection challenges Main challenge: Can’t observe all processes at the same instant • All processes observed so far (in set X ) may be passive • But a process q yet unobserved may send a message to a process p in X • turning p active when it receives the message • (but we have moved on, observing p was passive!) • And then q can turn passive itself 

6 .General strategy • Ensure all processes are passive • And no process observed as passive will ever turn active Is detecting termination similar to detecting something else? 

7 .Outline Termination Detection Ring termination (Dijkstra et al.) Misra’s Algorithm 

8 .Assumptions • No messages are lost • Only active processes can send messages • Receipt of a message reactivates a passive process • There is a ring structure • P0 , P1 , P2 , Pn−1 , P0 • for termination messages, communication only between Pi and Pi−1 • other messages can have any other topology 

9 .General ideas • Uses a token per detection • Termination detection launched by a single process P0 • Sends token when it is passive • P0 sends token to Pn−1 • Pn−1 sends token to Pn−2 only when it is passive • To avoid “pseudo-termination” (i.e. passive when receiving token, but can be reactivated later), a token is given a colour • Initially white • If token is still white at end of complete journey of ring, termination has occurred 

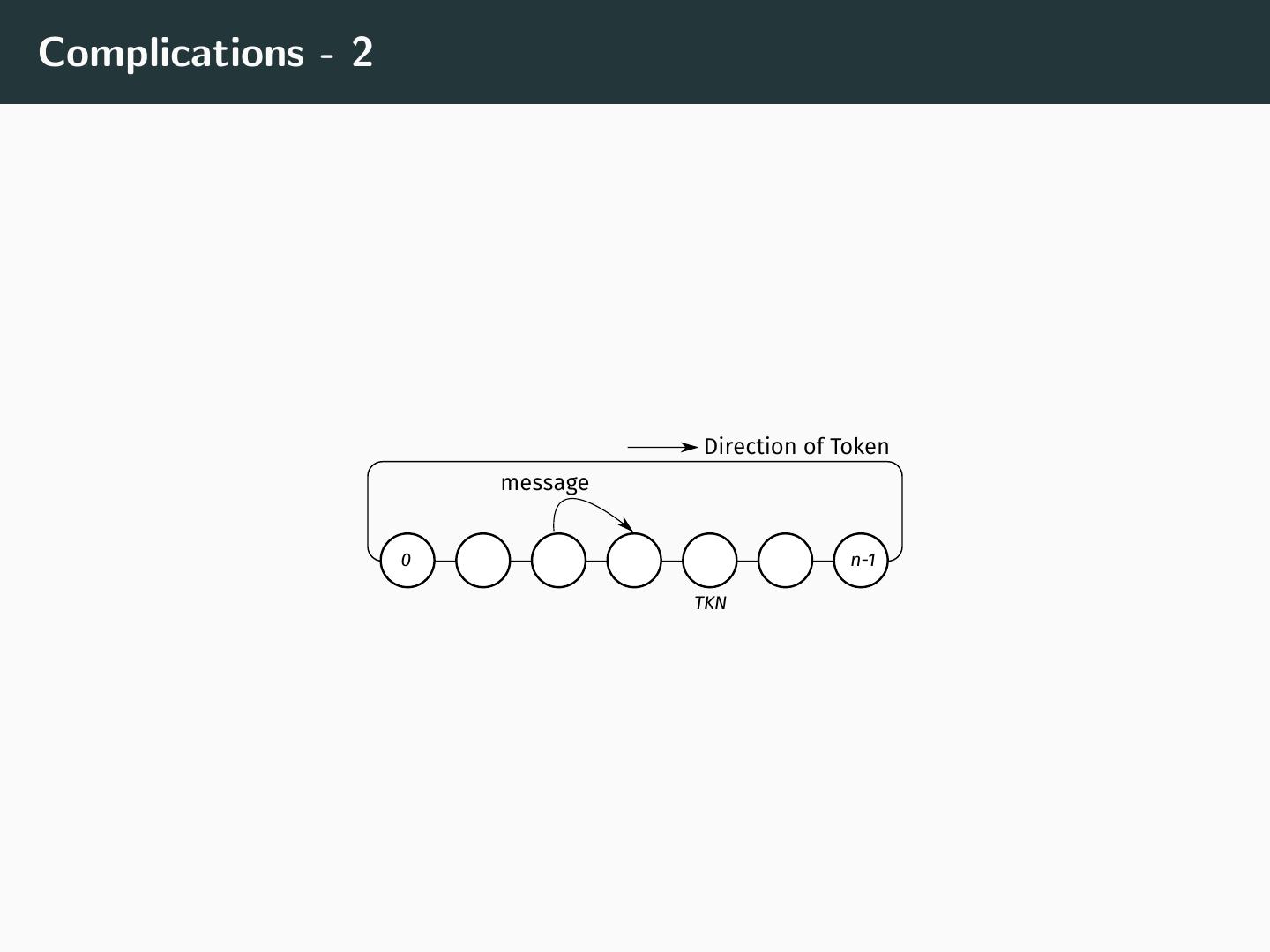
10 .Complications When a process that has not seen a token is about to send a message: • it does not know where the token is • this lack of knowledge causes issues • can result in “pseudo-termination” 

11 .Complications - 1 Direction of Token message 0 n-1 TKN 

12 .Complications - 2 Direction of Token message 0 n-1 TKN 

13 .Complications - 3 Direction of Token message 0 n-1 TKN 

14 .Handling messages in transit - 1 • All processes are also given a colour • Initially, white • Consider a process Pj not visited by the token • It may send a message to Pk reactivating it • What if k < j? • What if k > j? 

15 .Handling messages in transit - 2 • What if k > j? • Change process colour to black • If a white token encounters a white process, it forwards a white token • In all other cases, it forwards a black token • Once a token is forwarded, the colour of the process is reset to white 

16 .Outline Termination Detection Ring termination (Dijkstra et al.) Misra’s Algorithm 

17 .Where have we seen it before? What did we use Misra’s algorithm for last time? 

18 .Termination Detection using Markers • Useful for detecting loss of mutual exclusion token • Useful for termination detection • much simpler 

19 .Setup • No messages are lost • All messages between two processes are received in order • A marker is continously circulated • And contains a number n • All processes have a colour • Initially, black 

20 .Working of the algorithm (on a ring) • Assume a ring • A marker is sent only by an passive process • A marker colours a process white when it leaves • A process turns black if it is activated • How should the n inside the token behave? 

21 .Working of the algorithm on an arbitrary network - 1 • Assume processes are connected in an arbitrary graph • Vertices represent processes • Edges represent communication • I.e. processes x and y have different communication channel than • What complication does this create (vis-a-vis the ring?) • How can we solve it? 

22 .Working of the algorithm on an arbitrary network - 2 • Assume a strongly connected network • There exists a cycle in this network that includes every edge at least once • Precompute this cycle, of length c • When marker is forwarded, it is sent on next edge of this cycle • Termination detected when n == c 

23 .Arbitrary networks with no precomputation • Do we have to precompute the cycle? • Can’t we do this when forwarding the marker? • Can’t we forward markers in a distributed fashion? • How to choose edges? 

24 .Sketch • A depth first search of an undirected graph constructs the cycle in which all edges are present • See paper for the rest • Misra, Jayadev, ”Detecting Termination of Distributed Computations using Markers”, PODC 1983