05-Automated Parallelization in Software(Contd.)

1 .CSC2/458 Parallel and Distributed Systems Automated Parallelization in Software (Contd.) Sreepathi Pai February 1, 2018 URCS 

2 .Outline Characterizing loop dependences Identifying Loop Dependences Current Loop Optimizations 

3 .Outline Characterizing loop dependences Identifying Loop Dependences Current Loop Optimizations 

4 .Why characterize dependences? • The definition of dependence that we have used so far: • Two statements have a dependence if: • Both access same location (memory or register) • And one of the accesses is a write • This is not sufficient to reason about dependences in loops • We will extend this definition of dependences to loop dependence • Study additional characteristics of dependences 

5 .Already encountered characteristics of dependences • True dependence • S1 δS2 • S1 writes, S2 reads • Anti-dependence • S1 δ −1 S2 • S1 reads, S2 writes • Output dependence • S1 δ o S2 • Both S1 and S2 write 

6 .Loop-independent dependence • What are the dependences in the loop body below? • Can you change the order of the statements in the loop body? DO I = 1, 10 A(I) = A(I) + B C(I) = A(I) + D ENDDO • Can you change the (execution) order of loop iterations? Note: FORTRAN uses parentheses in array references: e.g., A(I) 

7 .Loop-independent dependences visualized A(0) = A(0) + B A(1) = A(1) + B A(2) = A(2) + B A(3) = A(3) + B C(0) = A(0) + D C(1) = A(1) + D C(2) = A(2) + D C(3) = A(3) + D NOTE: Only dependences from first four iterations visualized. 

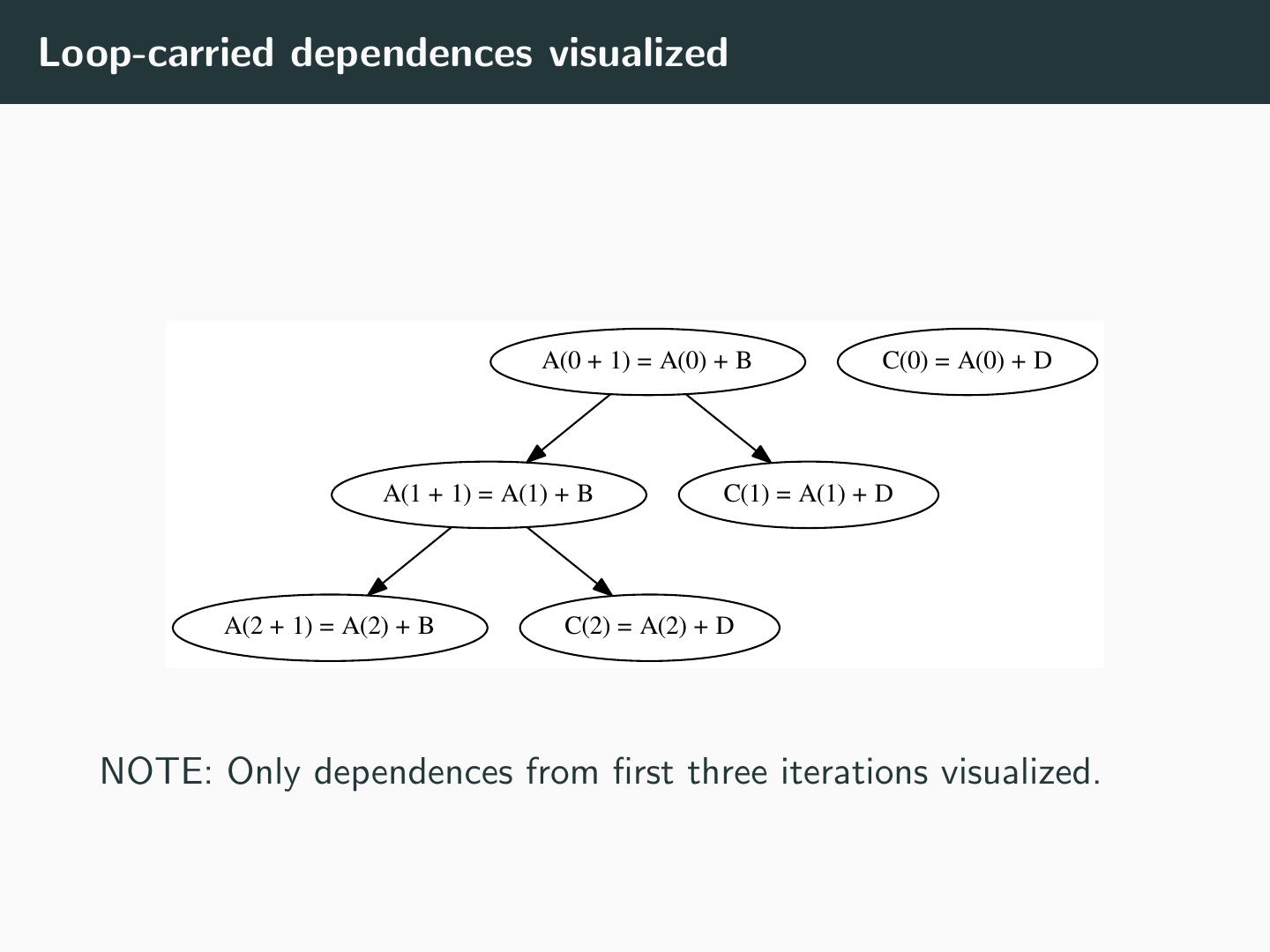
8 .Loop-carried dependences • What are the dependences in the loop body below? • Can you change the order of the statements in the loop body? DO I = 1, 10 A(I + 1) = A(I) + B C(I) = A(I) + D ENDDO • Can you change the (execution) order of loop iterations? 

9 .Loop-carried dependences visualized A(0 + 1) = A(0) + B C(0) = A(0) + D A(1 + 1) = A(1) + B C(1) = A(1) + D A(2 + 1) = A(2) + B C(2) = A(2) + D NOTE: Only dependences from first three iterations visualized. 

10 .Dependence Level for Loop-Carried Dependences DO I = 1, 10 DO J = 1, 2 A(I + 1, J) = A(I, J) + 1 ENDDO ENDDO • Can you change the order of inner loop? • Can you change the order of the outer loop? 

11 .Dependences Visualized A(0 + 1, 0) = A(0, 0) + 1 A(0 + 1, 1) = A(0, 1) + 1 A(1 + 1, 0) = A(1, 0) + 1 A(1 + 1, 1) = A(1, 1) + 1 A(2 + 1, 0) = A(2, 0) + 1 A(2 + 1, 1) = A(2, 1) + 1 NOTE: Only dependences from first three iterations visualized. 

12 .Loop Dependences • Loop-independent dependence • In same iteration, independent of loops • Loop-carried dependence • Across different iterations of atleast one loop • Dependence Level of a Loop-carried Dependence • The nesting level k of loop that carries the dependence • S1 δk S2 

13 .Iteration Spaces DO I = 1, 2 DO J = 1, 2 S ENDDO ENDDO • S has four instances (I , J): (1, 1), (1, 2), (2, 1), (2, 2) • Each of these values represents an iteration vector • Particular values of loop indices from outermost loop to innermost loop 

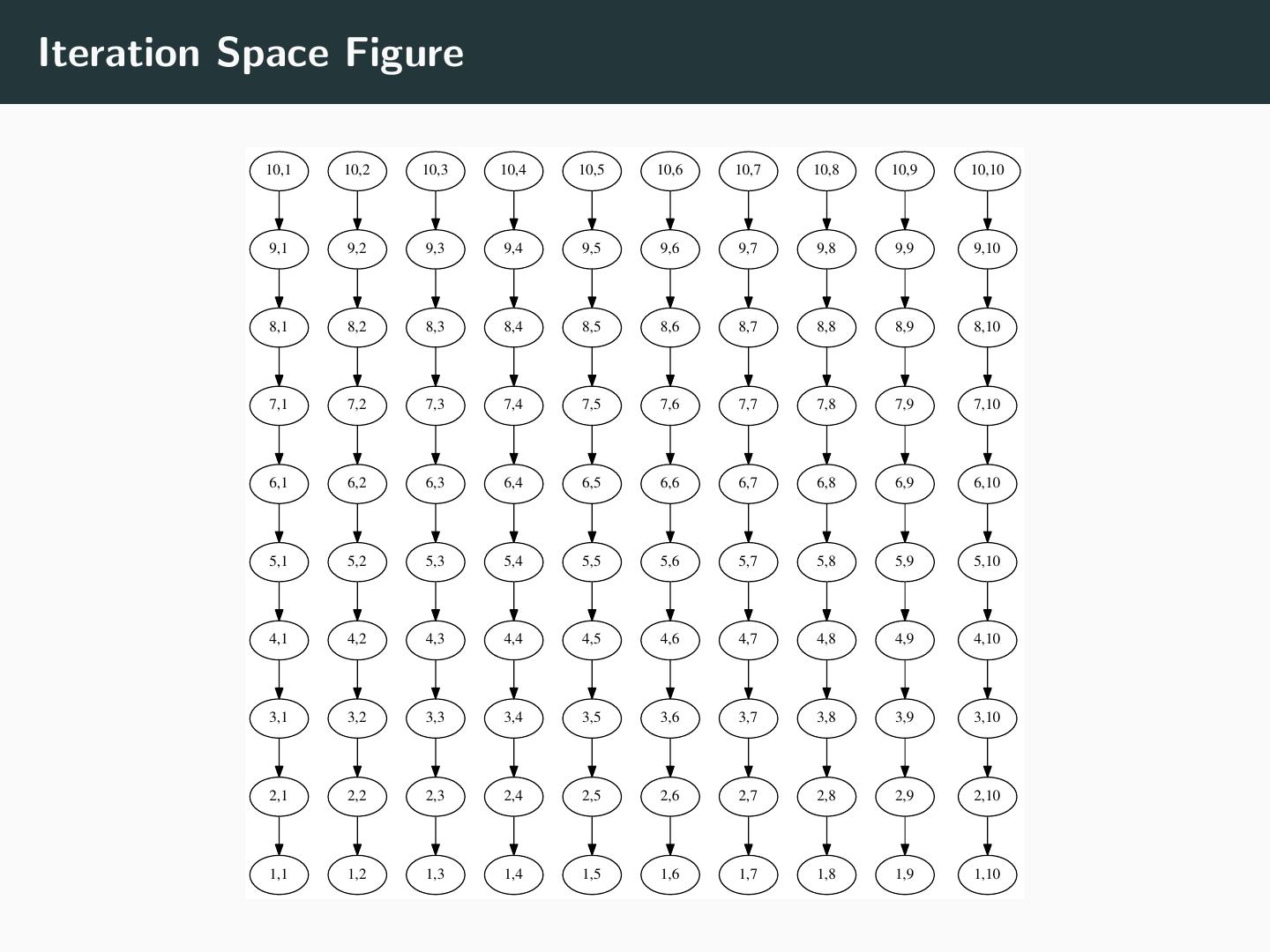
14 .Iteration Space Example DO J = 1, 10 DO I = 1, 10 A(I+1, J) = A(I, J) + X ENDDO ENDDO 

15 .Iteration Space Figure 10,1 10,2 10,3 10,4 10,5 10,6 10,7 10,8 10,9 10,10 9,1 9,2 9,3 9,4 9,5 9,6 9,7 9,8 9,9 9,10 8,1 8,2 8,3 8,4 8,5 8,6 8,7 8,8 8,9 8,10 7,1 7,2 7,3 7,4 7,5 7,6 7,7 7,8 7,9 7,10 6,1 6,2 6,3 6,4 6,5 6,6 6,7 6,8 6,9 6,10 5,1 5,2 5,3 5,4 5,5 5,6 5,7 5,8 5,9 5,10 4,1 4,2 4,3 4,4 4,5 4,6 4,7 4,8 4,9 4,10 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 3,10 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 2,10 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 1,10 

16 .Iteration Vector Ordering For two vectors i and j, each containing n elements, i < j is defined as: def lessthan(i, j, n): if n == 1: return i[0] < j[0] # test prefix for elementwise-equality if i[0:n-1] == j[0:n-1]: return i[n-1] < j[n-1] else: return lessthan(i, j, n-1) Can similarly define other order relations. 

17 .Loop dependence Statement S1 (source) depends on statement S2 (sink) if: • There exist iteration vectors i and j such that i < j or i = j • There is a path from S1 to S2 in the loop • S1 accesses memory M in iteration i • S2 accesses memory M in iteration j • and one of the accesses is a write 

18 .Distance Vectors d(i, j)k = jk − ik • Where i, j, d(i, j) are n-element vectors • ik indicates k-th element of i Example distance vector: (0, 1) 

19 .Direction Vectors D(i, j)k = • ”<”, if d(i, j)k > 0 • ”=”, if d(i, j)k = 0 • ”>”, if d(i, j)k < 0 Example direction vector for (0, 1): (=, <) 

20 .Information we need to track For every pair of memory references: • Iteration Vectors i and j which have a dependence, or • Unique Distance Vectors d(i, j), or • Unique Direction Vectors D(i, j) 

21 .Test • Which of these indicates a loop-independent dependence? • (=, =) • (=, <) • Of the loop-carried dependence in example above, what level is the loop-carried dependence? 

22 .Theorems WARNING: Informal language • Direction Vector Transform (Theorem 2.3 in AK) • If a transformation reorders loop iterations, and preserves the leftmost non-”=” component as ”<”, all dependences are preserved. • Theorem 2.4 in AK • If a level-k dependence exists, and a transformation reorders loop iterations while not reordering the level-k loop • And does not move loops inside k outside the loop and vice versa • It preserves all level-k dependences. • Iteration Reordering (Theorem 2.6 in AK) • Iterations of a level k loop can be reordered if there is no level k dependence. 

23 .Outline Characterizing loop dependences Identifying Loop Dependences Current Loop Optimizations 

24 .Generalizing Loop Indices DO I_1 = ... DO I_2 = ... ... DO I_N = ... A(f1, f2, f3, ..., fM) = ... ... = A(g1, g2, g3, ..., gM) ENDDO ENDDO ENDDO where A is M-dimensional array, and fX and gX are index functions of the form • fX (I 1, I 2, ..., I N) • gX (I 1, I 2, ..., I N) • 1 <= X <= M 

25 .Dependence using Iteration Vectors Let α and β be iteration vectors: • α = (i1 , i2 , i3 , ..., iN ) • β = (i1 , i2 , i3 , ..., iN ) Then a dependence exists if: • (vectors) α < β • fX (α) = gX (β), for 1 <= X <= M 

26 .Example DO J = 1, 10 DO I = 1, 10 A(I+1, J) = A(I, J) + X ENDDO ENDDO • f 1(J, I ) = I + 1, f 2(J, I ) = J • g 1(J, I ) = I , g 2(J, I ) = J • For α = (0, 0) (i.e. J = 0, I = 0) and β = (0, 1) (i.e. J = 0, I = 1): • f 1(α) = g 1(β), i.e. 1 = 1 • f 2(α) = g 2(β), i.e. 0 = 0 • Many other values of α and β also satisfy these equations. 

27 .Dependence Testing Do iteration vectors α and β exist such that: • (vectors) α < β • fX (α) = gX (β), for 1 <= X <= M How can we find α and β if they exist? 

28 .Restrictions on Index functions • fX and gX must be decidable • fX and gX must be ”analyzable” • to avoid brute force search • fX and gX must be a linear functions of loop indices: • i.e. for fX (i1 , i2 , i3 , ..., iN ) • fX = a1 i1 + a2 i2 + ... + an in + e • e is optional loop invariant calculation 

29 .Dependence Testing on Restricted Index Functions • Given that fX and gX are linear functions of loop indices • Do iteration vectors α and β exist such that: • (vectors) α < β • fX (α) = gX (β), for 1 <= X <= M How can we find α and β if they exist? What is this problem better known as?