07-Physical Memory

1 .Operating Systems 1 7. Physical Memory 7.1 Preparing a Program for Execution Program Transformations Logical-to-Physical Address Binding 7.2 Memory Partitioning Schemes Fixed Partitions Variable Partitions Buddy System 7.3 Allocation Strategies for Variable Partitions 7.4 Dealing with Insufficient Memory

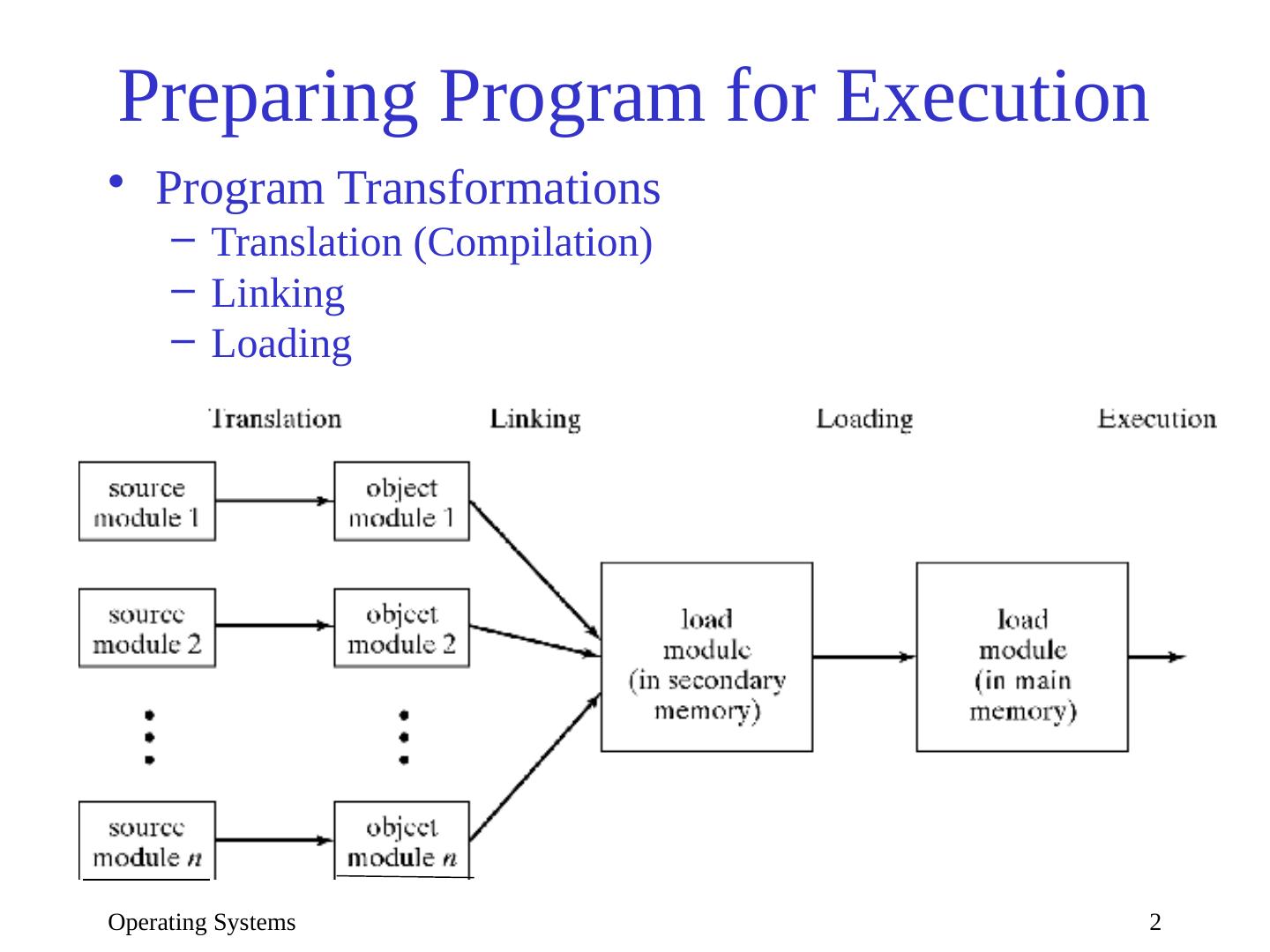
2 .Operating Systems 2 Preparing Program for Execution Program Transformations Translation (Compilation) Linking Loading

3 .Operating Systems 3 Address Binding Every logical address must be mapped to a physical address This may occur at once or in stages Each time the program is moved from one address space to another: Relocation Static binding Programming time Compilation time Linking time Loading time Dynamic binding Execution time

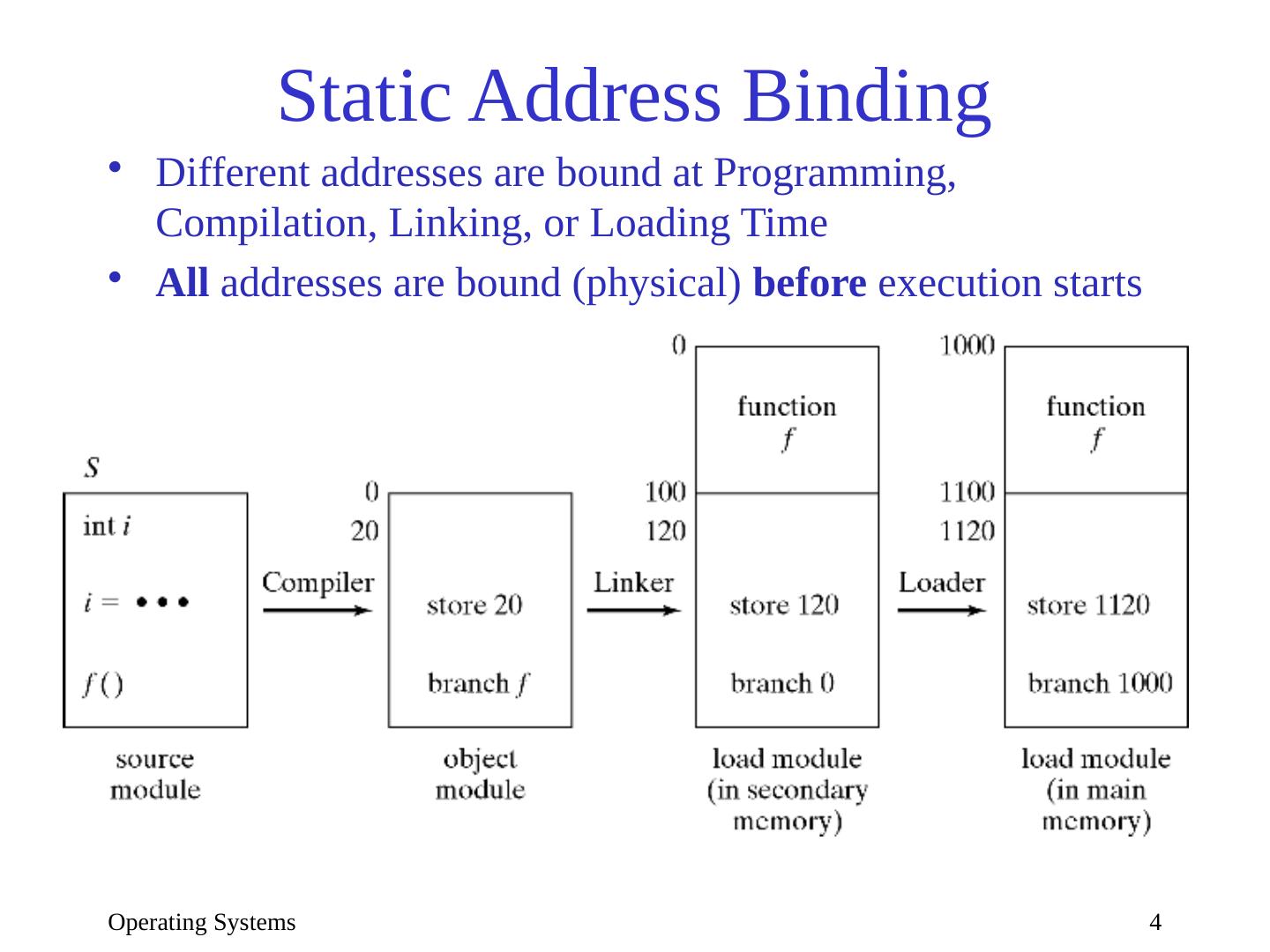
4 .Operating Systems 4 Static Address Binding Different addresses are bound at Programming, Compilation, Linking, or Loading Time All addresses are bound (physical) before execution starts

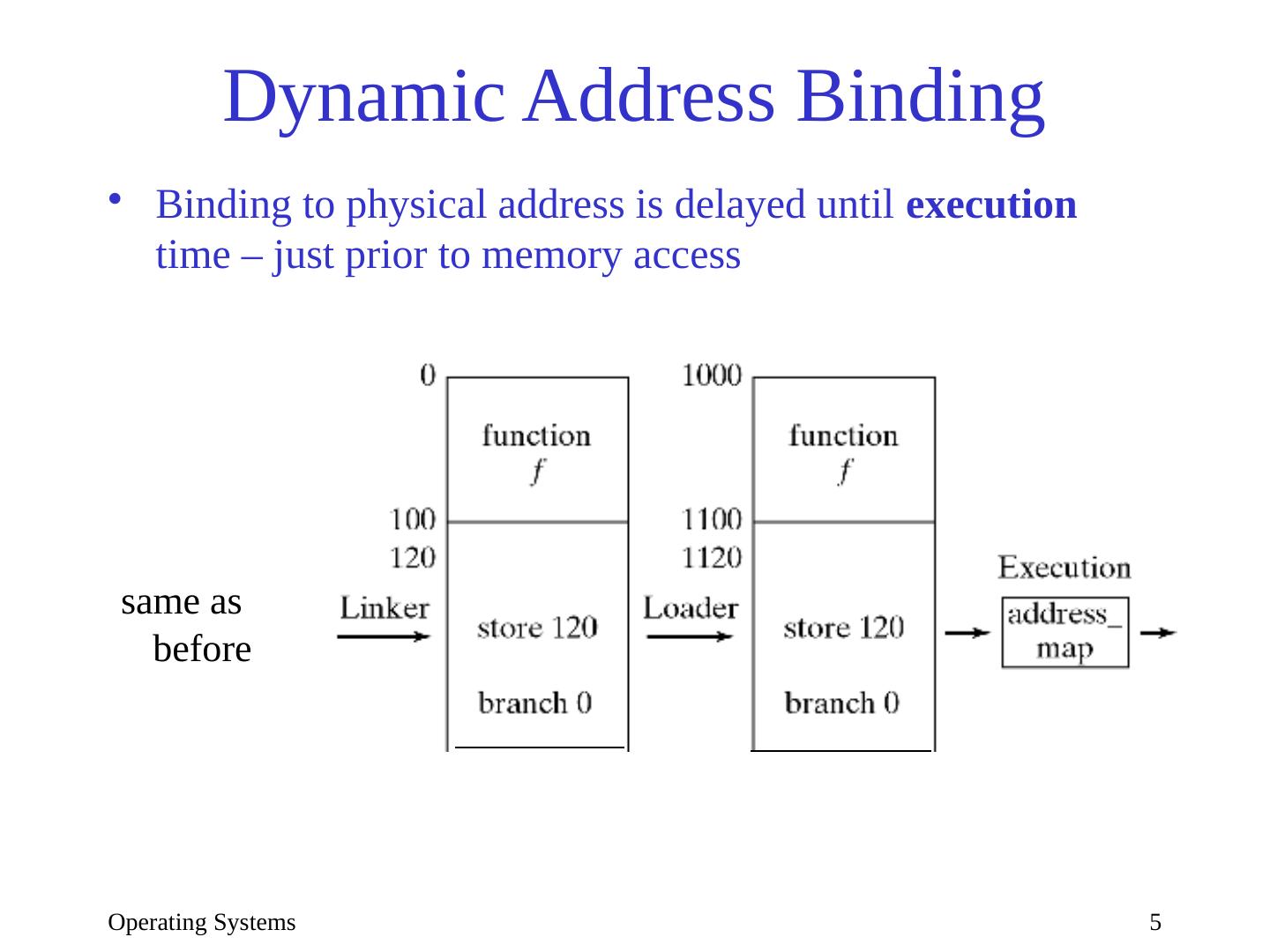
5 .Operating Systems 5 Dynamic Address Binding Binding to physical address is delayed until execution time – just prior to memory access same as before

6 .Operating Systems 6 Address Binding How to implement dynamic binding Must transform each address at run time: pa = address_map (la) Simplest form of address_map : Relocation Register : pa = la + RR More general form: Page or Segment Table (Chapter 8)

7 .Operating Systems 7 Memory Partitioning Schemes The problem: Memory is a single linear sequence Every program consists of several components (program, data, stack, heap) Some of the components are dynamic in size Multiple programs need to share memory How to divide memory to accommodate all these needs? Fixed partitions, variable partitions

8 .Operating Systems 8 Fixed Partitions Single-program system: 2 partitions (OS/user) System must manage dynamic data structures within each partition Multi-programmed systems: need n partitions Different-size partitions Program size limited to largest partition Internal fragmentation (unused space within partitions) How to assign processes to partitions ( scheduling : smallest possible, smallest available, utilization vs starvation) Same-size partitions (most common) Must permit each component to occupy multiple partitions (pages, Chapter 8)

9 .Operating Systems 9 Variable Partitions Memory not partitioned a priori Each request is allocated portion of free space Memory = Sequence of variable-size blocks Some are occupied, some are free (holes) External fragmentation occurs: many small holes Adjacent holes (right, left, or both) must be coalesced to prevent increasing fragmentation

10 .Operating Systems 10 Implementation How to keep track of holes and allocated blocks? Requirements: Must be able to efficiently: Find a hole of appropriate size Release a block (coalesce) Bitmap implementation Linked list implementation Problems: How to know the size of a hole or block How to know if neighbor is free or occupied

11 .Operating Systems 11 Linked List Implementation 1 Type , Size tags at the start of each b lock/hole Holes contain links to previous and next hole (why not blocks?) Checking neighbors of released block (e.g. C below): Right neighbor (easy): Use size of C Left neighbor (clever): Use sizes to find first hole to C ’s right, follow its back link to first hole on C ’s left, and check if it is adjacent to C . Holes must be sorted by physical address

12 .Operating Systems 12 Linked List Implementation 2 Better solution (due to Donald Knuth, Stanford U.) http :// en.wikipedia.org/wiki/Donald_knuth Replicate tags at both ends Checking neighbors of released block C : Right neighbor: Use size of C as before Left neighbor: Check its (adjacent) type , size tags Holes need not be sorted – insert is easier (append at end)

13 .Operating Systems 13 Bitmap Implementation Memory is divided into fix-size blocks Bitmap : binary string, 1 bit/block: 0 =free, 1 =allocated Implemented as char , integer, or byte array Example: B[0], B[1], … = 0010 0111, 0001 0000, … blocks 2, 5-7, 11 … are occupied Operations: Release : AND with 0 Allocate : OR with 1 Search for free block (look for 0): Repeat: AND with 1; if result=0 then stop, else consider next bit Operations use bit masks: M[0 ], M[1], …,M[7 ] = 1000 0000, 0100 0000,…, 0000 0001 M’[0],M’[1],…,M’[7] = 0111 1111, 1011 1111, …, 1111 1110

14 .Operating Systems 14 Example A 3 KB Free B 2 KB Occupied C 5 KB Free D 1 KB Occupied E 5 KB Free 000 11 000 00 1 00000 B[0] B[1] Assume Memory is broken into blocks of size 1KB Memory map is a byte array Release block D: B[1] = B[1] & 11011111‘ B[1] = B[1]

15 .Operating Systems 15 The Buddy System Compromise between fixed and variable partitions Fixed number of possible hole sizes; typically, 2 i Each hole can be divided (equally) into 2 buddies . Track holes by size on separate lists, 1 list for each partition size When n bytes requested, find smallest i so that n 2 i : If hole of this size is available, allocate it Otherwise, consider a larger hole: Recursively… split hole into two buddies continue with one, and place the other on appropriate free list for its size …until smallest adequate hole is created. Allocate this hole On release, recursively coalesce buddies Buddy searching for coalescing can be inefficient

16 .Operating Systems 16 The Buddy System Figure 7-9 Sizes: 1, 2, 4, 8, 16 3 blocks allocated & 3 holes left Block of size 1 allocated Block 12-13 released

17 .Operating Systems 17 Allocation Strategies with Variable Partitions Task: Given a request for n bytes, find hole ≥ n Goals: Maximize memory utilization (minimize external fragmentation) Minimize search time Search Strategies: First-fit : Always start at same place. Simplest. Next-fit : Resume search. Improves distribution of holes. Best-fit : Closest fit. Avoid breaking up large holes. Worst-fit : Largest fit. Avoid leaving tiny hole fragments First Fit is generally the best choice—how to measure?

18 .Operating Systems 18 Measures of Memory Utilization Compare number of blocks versus number of holes 50 % rule (Knuth, 1968 ): # holes = p × # full_blocks /2 p = probability of inexact match (i.e., remaining hole) In practice p=1 , because exact matches are highly unlikely, so #holes = # full_blocks /2 1/3 of all memory block are holes, 2/3 are occupied How much memory space is wasted? If average hole size = average full_block size then 33% of memory is wasted If average sizes are different?

19 .Operating Systems 19 How much space is unused (wasted) Utilization depends on the sizes ratio k = hole_size / block_size unused_memory = k/(k+2) Intuition: When k=1 , unused_memory1/3 (50% rule) When k  , unused_memory1 (100% empty) When k 0 , unused_memory0 (100% full) What determines k ? The block size b relative to total memory size M Determined experimentally via simulations: When bM /10 , k=0.22 and unused_memory0.1 When b=M/3 , k=2 and unused_memory0.5 Conclusion: M must be large relative to b

20 .Operating Systems 20 Dealing with Insufficient Memory Swapping Temporarily move process to disk Requires dynamic relocation Virtual memory ( Chapter 8) Allow programs large than physical memory Portions of programs loaded as needed Memory compaction Move blocks around to create larger holes How much and what to move?

21 .Operating Systems 21 Memory compaction Initial Complete Partial Minimal