09-Time and Global States

1 .CSS434 Time and Global States Textbook Ch11 Professor: Munehiro Fukuda CSS434 Time & Global States 1 

2 .Outline  Physical clock synchronization  Applications: make  Logical clock synchronization  Parallel and distributed simulation  Global states and consistent cuts  Distributed garbage collection, deadlock detection, distributed termination detection, and discrete-even simulation  Distributed debugging  Checking if a captured snapshot is one of transitory states we have considered. CSS434 Time & Global States 2 

3 . Why Clock Synchronization  Computer clock: a counter decremented by a crystal oscillation.  Single computers: all processes use the same clock. – No problem  Multiple computers: impossible to guarantee that the crystals in different computers all run at exactly the same frequency. Network  Synchronization:  Absolute (with real time)  Necessary for real-time applications such as on-line reservation systems  Relative (with each other)  Required for those applications that need a consistent view of time across all nodes. CSS434 Time & Global States 3 

4 . Clock Synchronization Passive Centralized Algorithms – Christian’s Algorithm T0 T1 Client Time? Time=T Time server Processing Time  Assumption: processing time has been measured or estimated  Message_delay = (T1 – T0 – processing)/2  New client time = T + message_delay  Improvements:  Average multiple measurements  Discard outlying measurements CSS434 Time & Global States 4 

5 . Clock Synchronization Active Centralized Algorithm – Berkeley Algorithm Time server Time? Diff(1) C1_time Client 1 Time? C2_time Diff(2) Client 2  Assumption: processing time has been measured or estimated  Server: diff(i) = server_time – (ci_time + message_deley)  Client: ci_time = ci_time + diff(i) CSS434 Time & Global States 5 

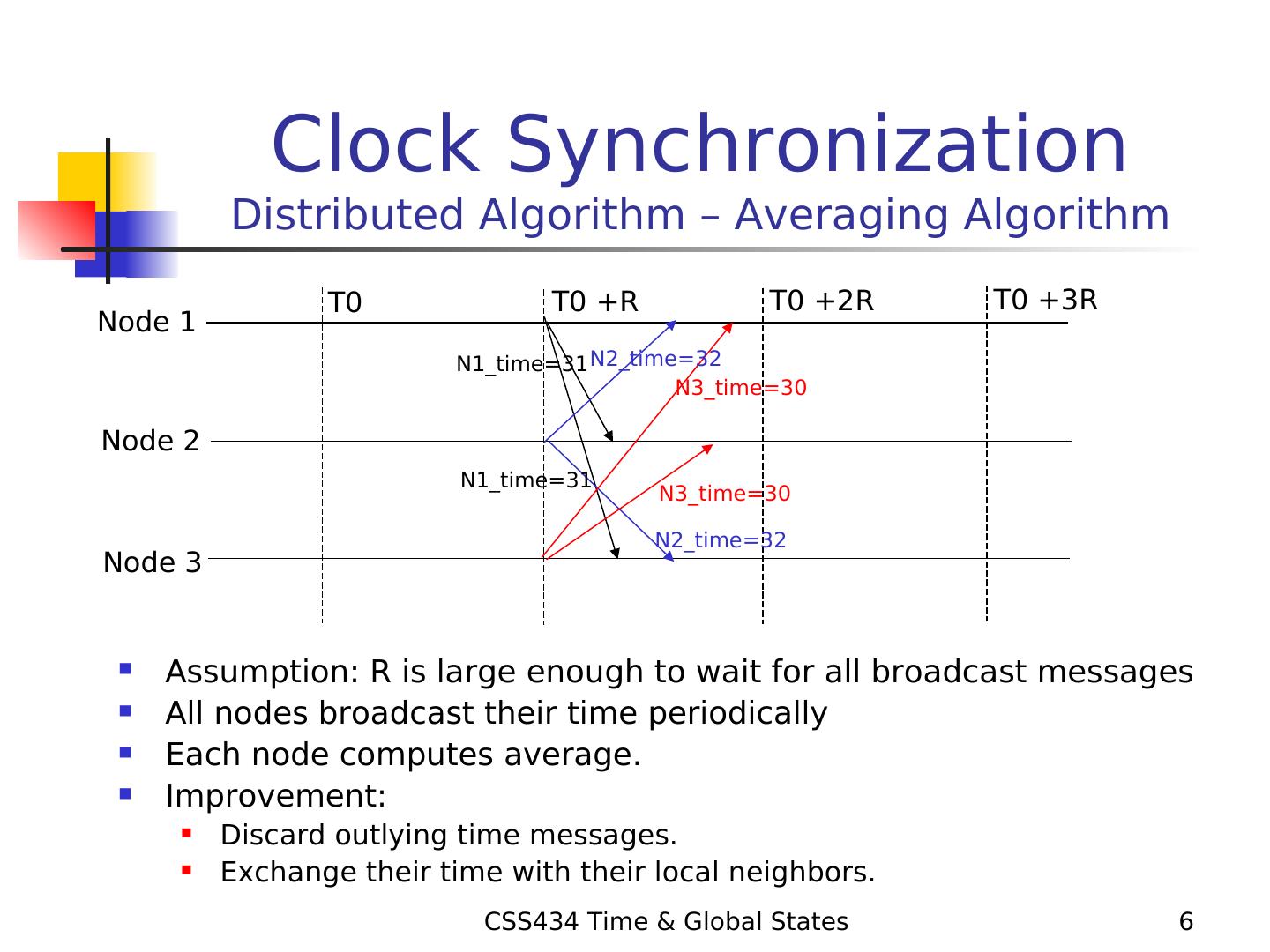
6 . Clock Synchronization Distributed Algorithm – Averaging Algorithm T0 T0 +R T0 +2R T0 +3R Node 1 N1_time=31 N2_time=32 N3_time=30 Node 2 N1_time=31 N3_time=30 N2_time=32 Node 3  Assumption: R is large enough to wait for all broadcast messages  All nodes broadcast their time periodically  Each node computes average.  Improvement:  Discard outlying time messages.  Exchange their time with their local neighbors. CSS434 Time & Global States 6 

7 . Clock Synchronization Network Time Protocol UTC (Coordinated Universal Time) 1 UDP message 2 2 3 3 3 Note: Arrows denote synchronization control, numbers denote strata. CSS434 Time & Global States 7 

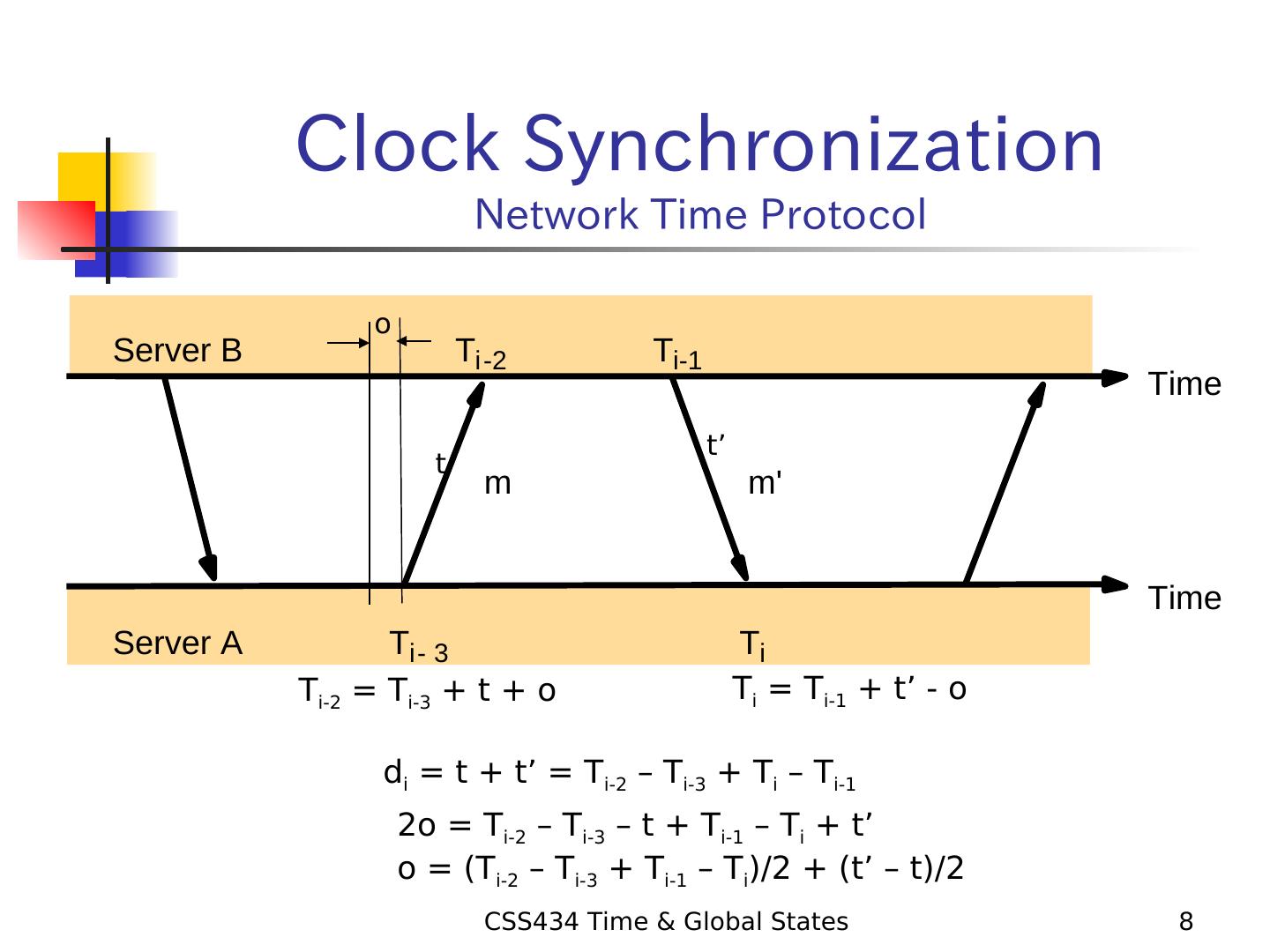
8 . Clock Synchronization Network Time Protocol o Server B Ti-2 Ti-1 Time t’ t m m' Time Server A Ti- 3 Ti Ti-2 = Ti-3 + t + o Ti = Ti-1 + t’ - o di = t + t’ = Ti-2 – Ti-3 + Ti – Ti-1 2o = Ti-2 – Ti-3 – t + Ti-1 – Ti + t’ o = (Ti-2 – Ti-3 + Ti-1 – Ti)/2 + (t’ – t)/2 CSS434 Time & Global States 8 

9 . Event Ordering Happened-Before Relation Most applications need not maintain the real-time synchronized clock. 1. Event 　 eki: The kth event of process i 2. Sequence 　 hki ： The history of process I through to the event eki 3. Cause-and-effect 　 e→e’: e proceeds e’. 4. Parallel events 　 e∥e’: e and e’ happen in parallele’: e and e’ happen in parallel 5. Happens-Before Relation: 1. If eki, eli ∈hhi and k < l, then eki → eli, 2. If ei = send(m) and ej = receive(m), then ei → ej, 3. If e → e’ and e’ → e”, then e → e” CSS434 Time & Global States 9 

10 . Event Ordering Logical Clock LC(ei) := (ei != receive(m)) ? LC + 1 : max(LC, TS(m)) + 1 where TS(m) is the timestamp of message m: P1 e11 e21 LC=1 LC=2 m1 P2 e12 e22 LC=3 LC=4 m1 P3 e13 e23 LC=1 LC=5 1. ee’ LC(e) < LC(e’) for all events 2. However, we cannot inferLC(e) < LC(e’)  ee’ Example: LC(e21) > LC(e13) but e21 || e13 CSS434 Time & Global States 10 

11 . Event Ordering Vector Clock Vi[I] = vi[i] + 1; Pi includes the value t = Vi in every message it sends Vi[j] = max(vi[j], t[j]) for j = 1,2,…,N P1 e11 e21 (1,0,0) (2,0,0) m1 (2,1,0) (2,2,0) P2 e 1 2 e 2 2 (0,0,1) m1 (2,2,2) P3 e1 3 e 2 3 1. ee’ V(e) < V(e’) 2. V(e) < V(e’)  ee’ Example:neither V(e21)  V(e13) nor V(e21)  V(e13), and thus e21 || e13 CSS434 Time & Global States 11 

12 . Global State Applications necessary to detect a correct global state p1 p2 object reference message a. Garbage collection garbage object This is not a garbage, because p1 p2 wait-forthe in-transit message points to it b. Deadlock wait-for Both p1 and p2 are passive and thus seems ready to finish, but an in-transit message makes p1 active again. p1 p2 activate c. Termination passive passive CSS434 Time & Global States 12 

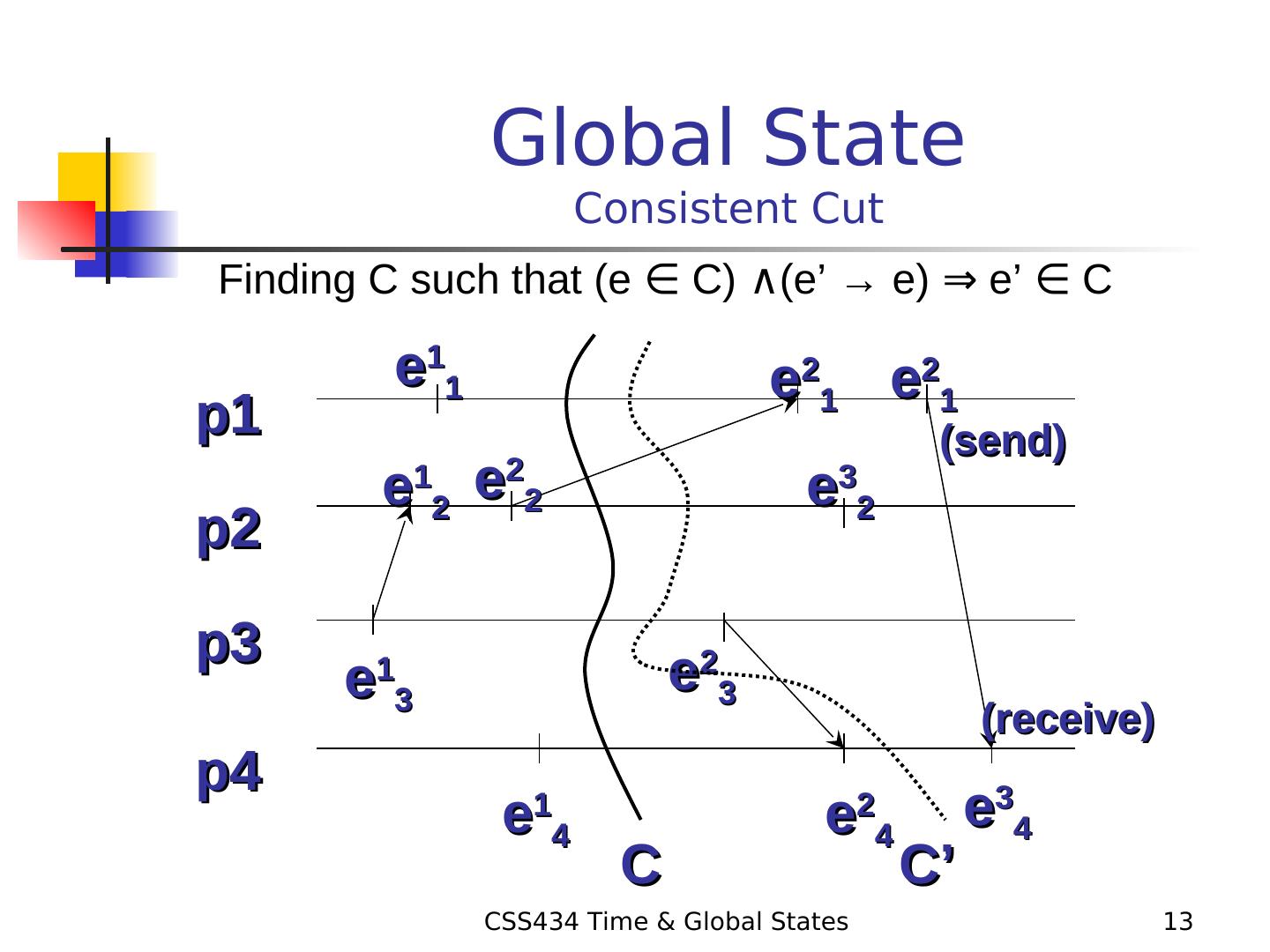
13 . Global State Consistent Cut Finding C such that (e ∈ C) ∧(e’ → e) ⇒ e’ ∈ C C) ∧(e’ → e) ⇒ e’ ∈ C(e’ → e) ⇒ e’ ∈ C e’ ∈ C) ∧(e’ → e) ⇒ e’ ∈ C C e11 e21 e21 p1 (send) e12 e22 e32 p2 p3 e13 e23 (receive) p4 e 1 4 e 2 4 e34 C C’ CSS434 Time & Global States 13 

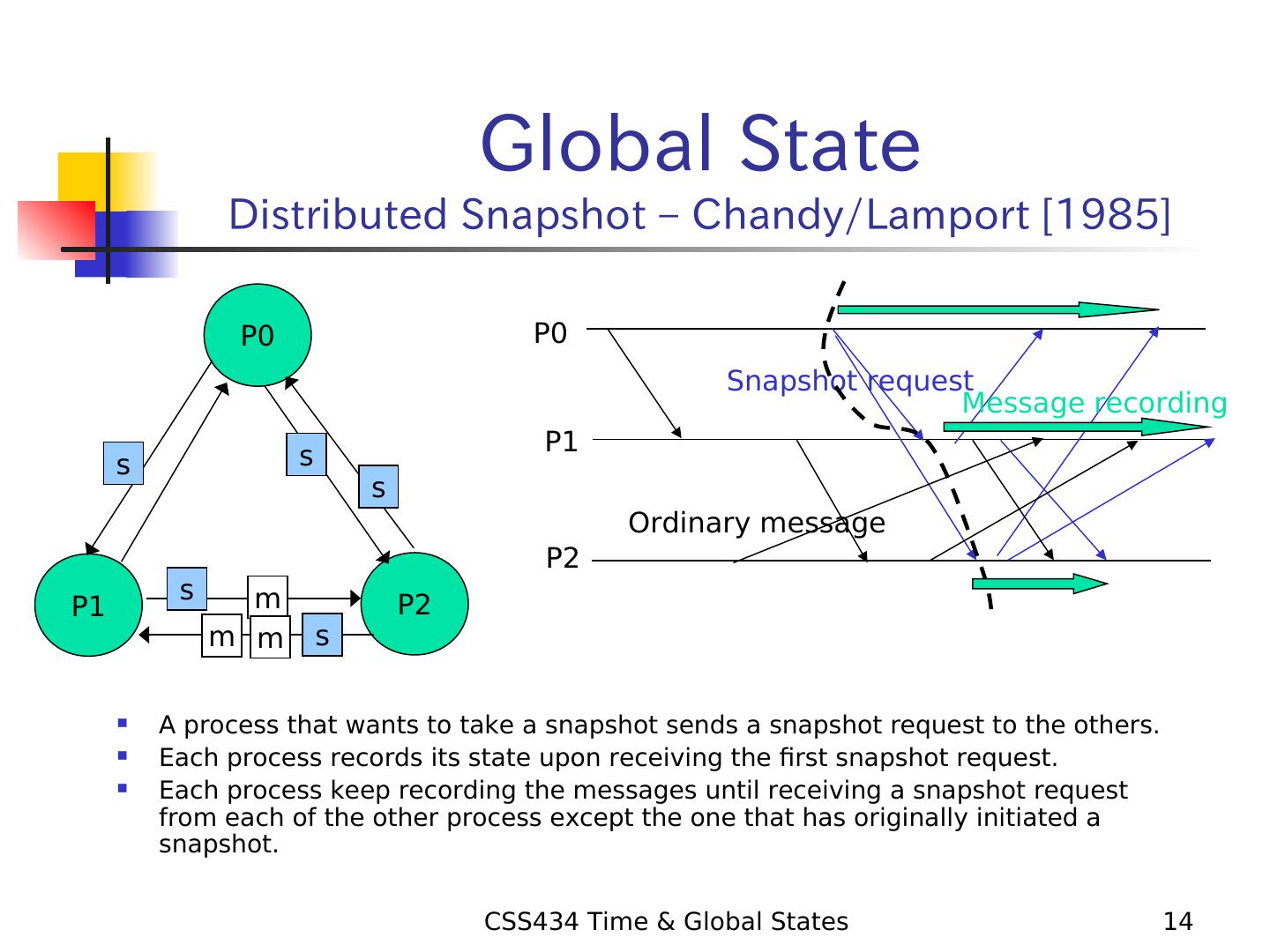
14 . Global State Distributed Snapshot – Chandy/Lamport [1985] P0 P0 Snapshot request Message recording s P1 s s Ordinary message P2 s m P1 P2 m m s  A process that wants to take a snapshot sends a snapshot request to the others.  Each process records its state upon receiving the first snapshot request.  Each process keep recording the messages until receiving a snapshot request from each of the other process except the one that has originally initiated a snapshot. CSS434 Time & Global States 14 

15 . Global State Distributed Snapshot – Chandy/Lamport [1985] Marker (Snapshot request) receiving rule for process p i On pi’s receipt of a marker (snapshot request) message over channel c: if (pi has not yet recorded its state) it records its process state now; records the state of c as the empty set; turns on recording of messages arriving over other incoming channels; else pi records the state of c as the set of messages it has received over c since it saved its state. end if Marker (Snapshot request) sending rule for process p i After pi has recorded its state, for each outgoing channel c: pi sends one marker message over c (before it sends any other message over c). CSS434 Time & Global States 15 

16 . A Distributed Snapshot Example 1. Global state S 0 <$1000, 0> p1 c2 (empty) p2 <$50, 2000> Start recording its state c1 (empty) Consistent Cut 2. Global state S 1 <$900, 0> p1 c2 (Order 10, $100), M p2 <$50, 2000> c1 (empty) 3. Global state S 2 <$900, 0> p1 c2 (Order 10, $100), M p2 <$50, 1995> Stop recording c1 (five widgets) M Record its state 4. Global state S 3 <$900, 5> p1 c2 (Order 10, $100) p2 <$50, 1995> Time line c1 (empty) (M = marker message) CSS434 Time & Global States 16 

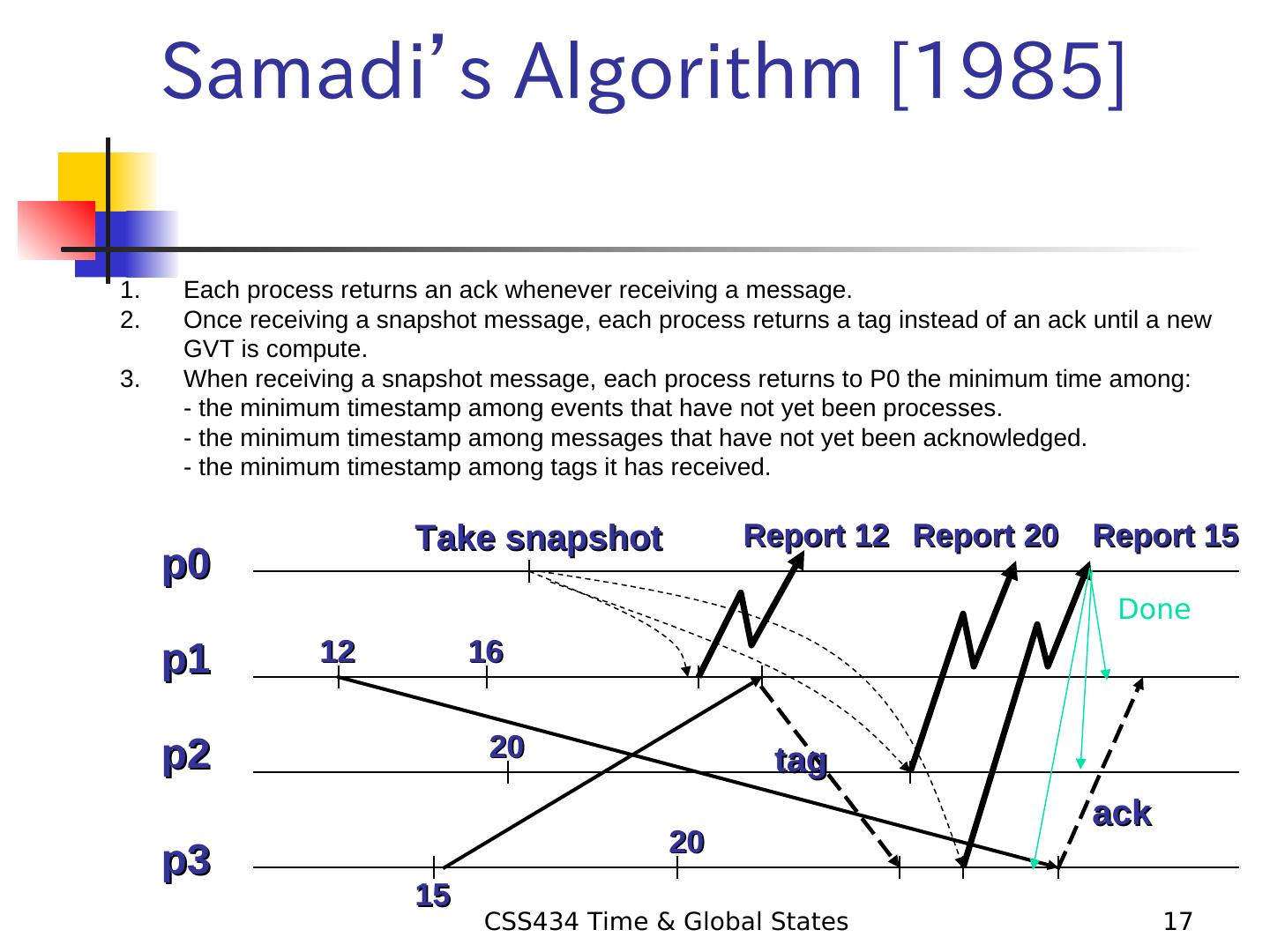
17 . Samadi’s Algorithm [1985] 1. Each process returns an ack whenever receiving a message. 2. Once receiving a snapshot message, each process returns a tag instead of an ack until a new GVT is compute. 3. When receiving a snapshot message, each process returns to P0 the minimum time among: - the minimum timestamp among events that have not yet been processes. - the minimum timestamp among messages that have not yet been acknowledged. - the minimum timestamp among tags it has received. Take snapshot Report 12 Report 20 Report 15 p0 Done p1 12 16 p2 20 tag ack 20 p3 15 CSS434 Time & Global States 17 

18 . Mattern’s Algorithm [1993] 1. Process Pi maintains a vector counter: Vi[1..n]. 2. Pi writes in Vi[j] the number of messages sent to Pj. 3. Pi subtract one from Vi[j] when receiving a message from Pj 4. During the 1st circulation of a ‘take snapshot’ message, Pi performs: C[1..n]+=Vi[1..n]; Vi[1..n] = 0 Upon completing the 1st circulation, c[I] presents the number of messages in trans it to Pi. 5. During the 2nd circulation, Pi wait for performs: C[i] = 0 1st snapshot +1 p1 (0,0,1,1) -1 +1 +1 -1 2nd snapshot p2 (0,0,0,1) +1 -1 -1 p3 (0,2,-1,0) (0,0,0,0) +1 -1 p4 (0,1,0,0) (0,0,1,0) (0,0,0,0) CSS434 Time & Global States 18 

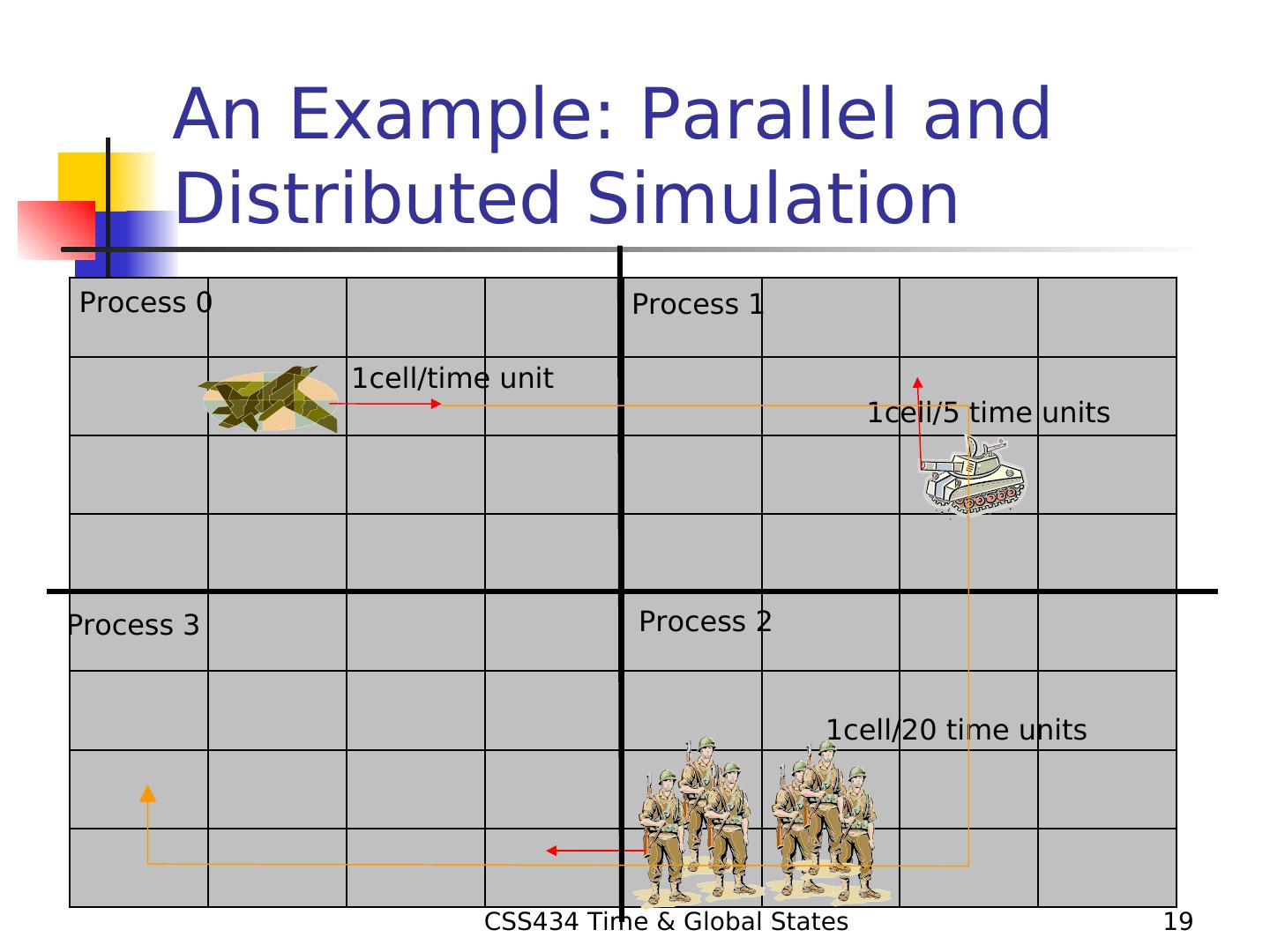
19 . An Example: Parallel and Distributed Simulation Process 0 Process 1 1cell/time unit 1cell/5 time units Process 3 Process 2 1cell/20 time units CSS434 Time & Global States 19 

20 . An Example: Parallel and Distributed Simulation (Cont’d) Barrier per every simulation cycle Process 0 e1 e2 e3 e4 What drawbacks does this method have? attack Process 1 e5 e6 e7 e1 Process 2 attack e1 e8 e9 e10 e11 e12 Process 3 CSS434 Time & Global States 20 

21 . An Example: Parallel and Distributed Simulation (Cont’d) Discrete event simulation with optimistic synchronization Old event history kept so as to rollback computation. Process 0 e1 e2 e3 e4 When can we garbage collect such history? attack Process 1 e5 e6 e7 e1 e2 e3 Rollback Process 2 attack e1 e8 e9 e10 e11 e12 Rollback Process 3 e13 e14 CSS434 Time & Global States 21 

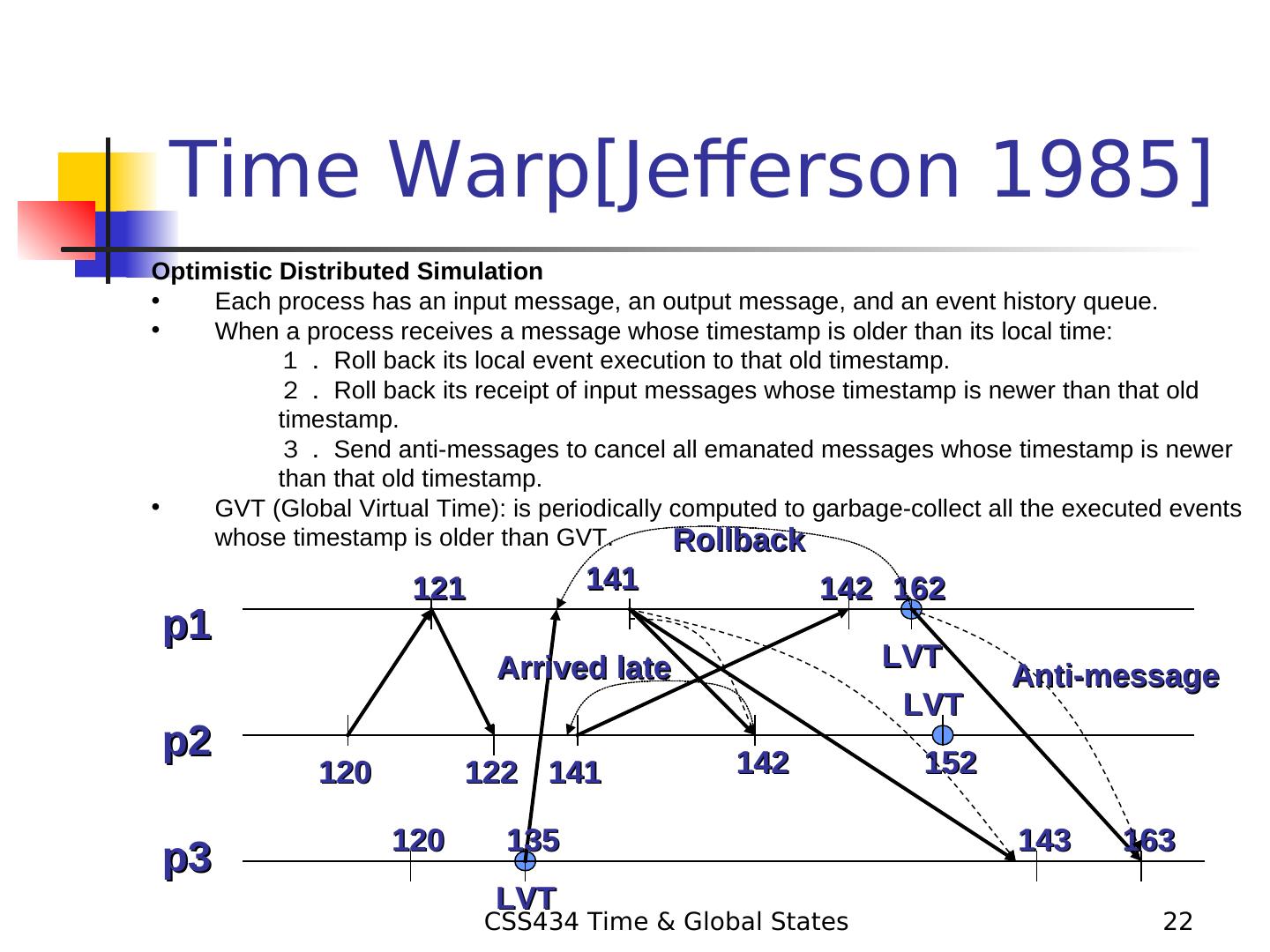
22 . Time Warp[Jefferson 1985] Optimistic Distributed Simulation • Each process has an input message, an output message, and an event history queue. • When a process receives a message whose timestamp is older than its local time: 　 １． Roll back its local event execution to that old timestamp. 　 ２． Roll back its receipt of input messages whose timestamp is newer than that old timestamp. ３． Send anti-messages to cancel all emanated messages whose timestamp is newer than that old timestamp. • GVT (Global Virtual Time): is periodically computed to garbage-collect all the executed events whose timestamp is older than GVT. Rollback 121 141 142 162 p1 Arrived late LVT Anti-message LVT p2 142 152 120 122 141 120 135 143 163 p3 LVT CSS434 Time & Global States 22 

23 . SPEEDS[Steinman 1992] Breathing Time Buckets This is an optimistic distributed simulator, but so aggressive as Time Warp. • Each process broadcasts the oldest local even among those it will execute. This is called a Local Event Horizon (LEH). • A process must suspend its even processing if it has received an older LEH than the one it is currently processing. • The oldest LEH among all processes become the next Global Event Horizon (GEH). • Each process may send out all messages and process all events before this new GEH. • Processes which have already processed beyond GEH must roll back their computation to GEH. No anti-messages are sent out. P1’s LEH p1 p2 Next GEH (GVT) P2’s LEH CSS434 Time & Global States 23 

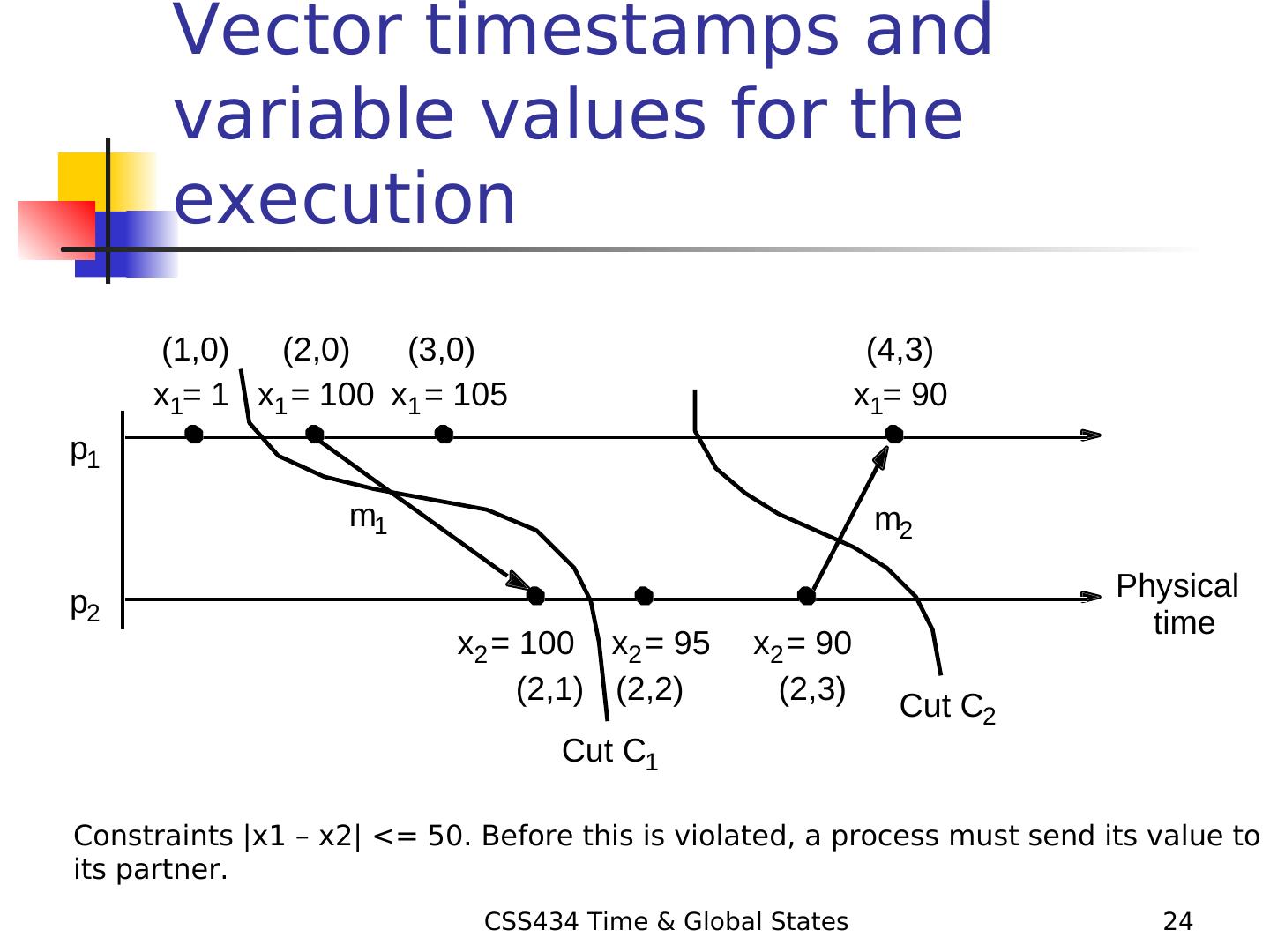
24 . Vector timestamps and variable values for the execution (1,0) (2,0) (3,0) (4,3) x1= 1 x1 = 100 x1 = 105 x1= 90 p1 m1 m2 p2 Physical time x2 = 100 x2 = 95 x2 = 90 (2,1) (2,2) (2,3) Cut C2 Cut C1 Constraints |x1 – x2| <= 50. Before this is violated, a process must send its value to its partner. CSS434 Time & Global States 24 

25 . The lattice of global states for the execution Level 0 S 00 1 S 10 2 S 20 Sij= global state after i events at process 1 and j events at process 2 3 S30 S21 4 S31 S 22 5 S32 S23 6 S 33 7 S 43 CSS434 Time & Global States 25 

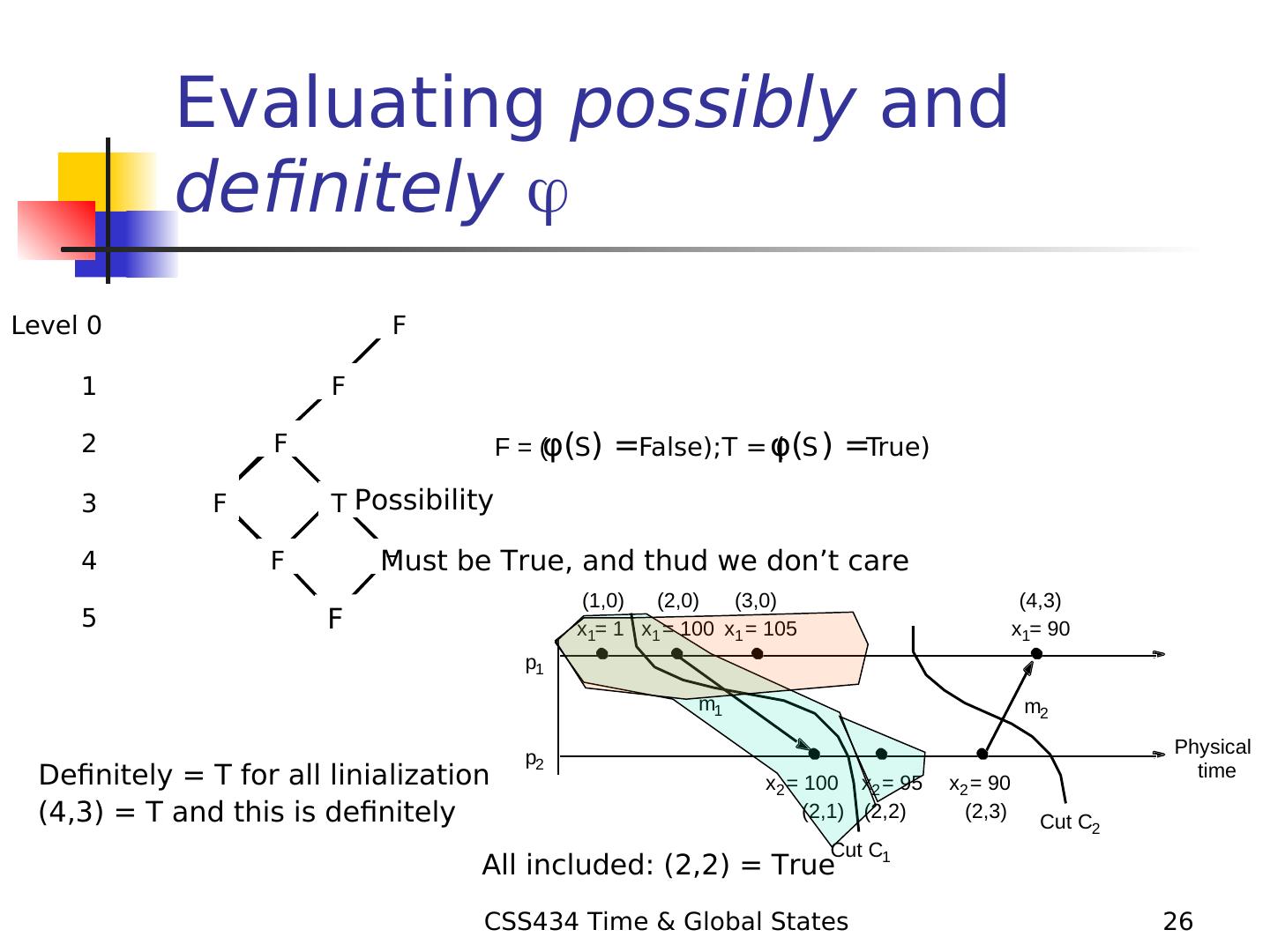
26 . Evaluating possibly and definitely  Level 0 F 1 F 2 F F = (φ(S) =False);T = φ( ( S ) =True) 3 F T Possibility 4 F – Must be True, and thud we don’t care (1,0) (2,0) (3,0) (4,3) 5 ?F x1= 1 x1 = 100 x1 = 105 x1= 90 p1 m1 m2 p2 Physical Definitely = T for all linialization x2 = 100 x2 = 95 x2 = 90 time (4,3) = T and this is definitely (2,1) (2,2) (2,3) Cut C2 Cut C1 All included: (2,2) = True CSS434 Time & Global States 26 

27 . Paper Review by Students  Distributed Snapshot  Samadi’s Algorithm  Mattern’s Algorithm  Discussions: What are pros & cons of these algorithms?  Optimistic Synchronization  SPEEDS  Time Warp  Discussions: What are pros & cons of these algorithms in terms of performance, process creation/termination, dynamic memory allocation, and I/O handling? CSS434 Time & Global States 27 

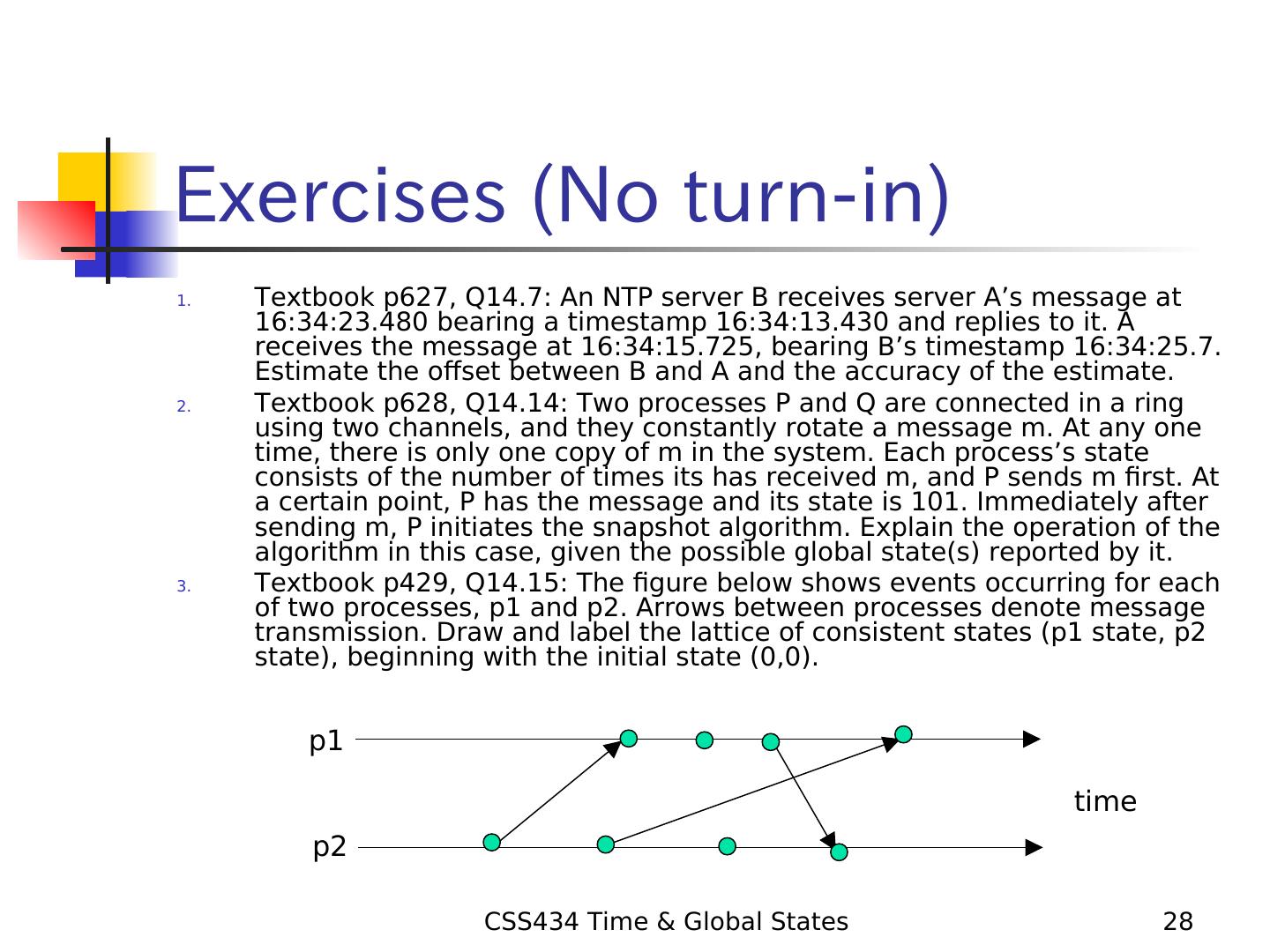
28 .Exercises (No turn-in) 1. Textbook p627, Q14.7: An NTP server B receives server A’s message at 16:34:23.480 bearing a timestamp 16:34:13.430 and replies to it. A receives the message at 16:34:15.725, bearing B’s timestamp 16:34:25.7. Estimate the offset between B and A and the accuracy of the estimate. 2. Textbook p628, Q14.14: Two processes P and Q are connected in a ring using two channels, and they constantly rotate a message m. At any one time, there is only one copy of m in the system. Each process’s state consists of the number of times its has received m, and P sends m first. At a certain point, P has the message and its state is 101. Immediately after sending m, P initiates the snapshot algorithm. Explain the operation of the algorithm in this case, given the possible global state(s) reported by it. 3. Textbook p429, Q14.15: The figure below shows events occurring for each of two processes, p1 and p2. Arrows between processes denote message transmission. Draw and label the lattice of consistent states (p1 state, p2 state), beginning with the initial state (0,0). p1 time p2 CSS434 Time & Global States 28