展开查看详情
2 .2 运算符重载 为什么要“运算符重载” 那些运算符可以重载，哪些不可以 如何实现运算符重载 实现方式：成员函数与非成员函数 类型转换 怎样实现对象与基本数据类型数据的运算
3 .3 预定义的运算符 只针对基本数据类型 ，若要对类的对象进行类似的运算， 需要重新定义运算符的功能 。 运算符重载实质就是函数重载： 对已有的运算符赋予多重含义，使得同一个运算符作用于不 同类型的数据时导致不同的行为。 为什么要运算符重载 int x=1, y=2, z; z = x + y; // 普通数据类型的加法 例： Point A(1,2), B(3,4), C; C = A + B; // Point 类对象的加法 String str1(“hello”), str2(“Math”), str3; str3 = str1 + str2; // String 类对象的加法 如何 实现？
4 .4 只能重载 已有的运算符 重载 不改变 运算符的优先级和结合率 运算符重载 不改变 运算符的操作数的数目 重载的功能通常与已有的功能类似 运算符重载是针对 新类型数据（类与对象） 的需要， 因此 至少有一个操作数是新类型数据 运算符重载基本规则 不能被重载的四个运算符： . .* :: ?:
5 .5 如何实现运算符重载 定义运算符重载的一般形式 类型说明符 operator 运算符 ( 形参列表 ) { 函数体 ; } // 在类的声明中定义 这里的 类型说明符 可以是 类名 或 基本数据类型 Complex Complex:: operator+ (Complex & c2) { return C omplex(real+c2.real, imag+c2.imag); } 例： 类型说明符 类名 :: operator 运算符 ( 形参列表 ) { 函数体 ; } // 假定在外部定义
6 .6 实现方式一：成员函数方式 运算符重载可以通过 成员函数 实现 运算符重载为成员函数时， 形参个数少一个 ： 目的对象自动作为第一个操作数 / 左操作数 如果是单目运算，无需形参（后置 ++ 和后置 -- 除外） 优点：可以自由访问本类的数据成员 若是双目运算，则左操作数就是目的对象本身 若是单目运算，则目的对象就是操作数，不需要其它对象
7 .7 例： 有理数的加法 class Rational { public: Rational() { x=0; y=1; } Rational( int x, int y) { this->x=x; this->y=y; } Rational operator+( const Rational & p); private: int x, y; }; Rational Rational:: operator+ ( const Rational & p) { int newx = x* p.y + y* p.x ; int newy = y* p.y ; return Rational( newx , newy ); } ex11_overload01.cpp
8 .8 实现方式一：成员函数 对象 A ⊙ 对象 B 双目运算符的重载（成员函数） 重载双目运算符 ⊙ （成员函数）： 只有一个形参（ 对象 ） 类型说明符 类名 ::operator⊙( const 类名 &p) { 函数体 ; } 类型说明符 operator⊙( const 类名 &); 声明 定义 （在类外部定义）
9 .9 实现方式一：成员函数 重载前置单目运算符 ⊙ （成员函数方式）：没有形参 ⊙ 对象 A 前置单目运算符的重载（成员函数） 类名 类名 ::operator⊙() { 函数体 ; } 类名 operator⊙(); 声明 定义 （在类外部定义）
10 .10 实现方式一：成员函数 重载后置单目运算符 ⊙ （成员函数方式）： 带一个整型形参，该形参在运算中不起任何作用， 只用于区分前置和后置 ，因此也称为伪参数。 对象 A ⊙ 后置单目运算符 （ ++ 、 -- ） 的重载（成员函数） 类名 类名 ::operator⊙( int dummy) { 函数体 ; } 类名 operator⊙( int ); 声明 定义 （在类外部定义）
11 .11 例： 重载单目运算符 class Clock { public: Clock( int H=0, int M=0, int S=0); void showTime () const // 显示时间 { cout <<hour<<":"<<minute<<":"<<second<< endl ; } Clock operator++(); // 前置单目运算符重载 Clock operator++( int ); // 后置单目运算符重载 private: int hour, minute, second; }; Clock::Clock( int H, int M, int S) // 构造函数 { i f(0<=H && H<24 && 0<=M && M<60 && 0<=S && S<60) { hour = H; minute = M; second = S; } else cout <<"Time error!"<< endl ; }
12 .12 例： 重载单目运算符 Clock Clock::operator++() // 前置单目运算符重载函数 { second++; if(second >= 60) { second -= 60; minute++; if(minute >= 60) { minute -= 60; hour = (++hour) % 24; } } return *this; } Clock Clock::operator++( int ) // 后置单目运算符重载 { // 注意形参表中的整型参数 Clock old=*this; ++(*this); // 调用前置 ++ return old; } ex11_overload02.cpp
13 .13 实现方式二：非成员函数 非成员函数 方式实现运算符重载 - 在相关类中将其声明为 友元函数， 在类外部定义 - 形参个数与操作数相同 - 所有操作数都通过 参数传递 Complex operator+( const Complex &c1, const Complex &c2) { return complex(c1.real+c2.real, c1.imag+c2.imag); } 例：
14 .14 例： 有理数的减法 class Rational { public: Rational() { x=0; y=1; } Rational( int x, int y) { this->x=x; this->y=y; } friend Rational operator - ( const Rational &p1, const Rational &p2); private: int x, y; }; Rational operator-( const Rational &p1, const Rational &p2) { int newx = p1.x*p2.y – p1.y*p2.x; int newy = p1.y*p2.y; return Rational( newx , newy ); } ex11_overload03.cpp
15 .15 重载 [] int Rational::operator[]( int idx ) { if ( idx == 0) return x; else return y; } 为什么要重载 [ ] 在数组中，可以通过 [ ] 来引用指定位置的元素。在 Rational 类中，我们希望用 a[0] 表示分子， a[1] 表示分母。 Rational a(4,5); cout << a[0] << “/” << a[1] << endl ; // OK a[0] = 3; // ???
16 .16 左值 int & Rational::operator[]( int idx ) { if ( idx == 0) return x ; else return y ; } ex11_overload04.cpp 什么是左值？ 能出现在赋值号左边的量称为左值 ( Lvalue ) 怎样使得 r[0] 能出现在赋值号左边？ 返回 r[0] 的引用
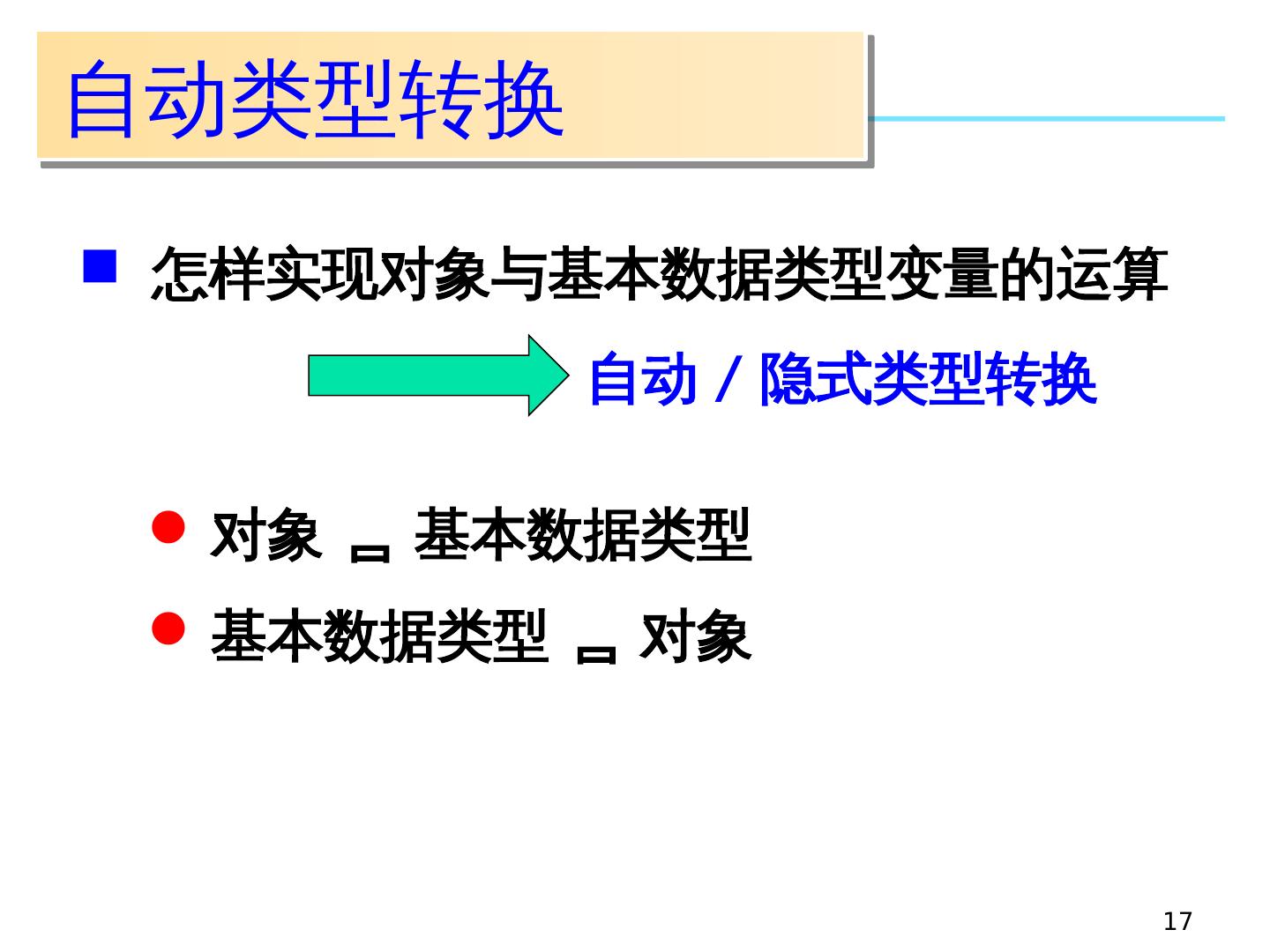
17 .17 自动类型转换 怎样实现对象与基本数据类型变量的运算 对象 基本数据类型 基本数据类型 对象 自动 / 隐式类型转换
18 .18 基本数据类型 对象 例： 有理数与 整型 数据的加法运算 Rational a(1,2), b; int c=3; b = a + c; // 怎么实现？ 通过 构造函数 ，将整型数据自动转换为有理数，然后参与运算 class Rational { public: Rational() { x=0; y=1; } Rational( int x, int y) { this->x=x; this->y=y; } Rational( int x) { this->x=x; y=1; }; ... ... private: int x, y; }; ex11_overload05.cpp
19 .19 对象 基本数据类型 例： 有理数与双精度数的加法运算 Rational a(1,2); double b=0.8, c; c = a + b; // 怎么实现？ 将有理数转换为双精度数，然后参与运算 实现方式：重载类型转换函数（只能作为成员函数） operator 转换函数名 () { 函数体 }; 类名 :: operator 转换函数名 () { 函数体 }; // 假定在外部定义 没有返回数据类型！
20 .20 例： 自动类型转化 class Rational { public: Rational() { x=0; y=1; } Rational( int x, int y) { this->x=x; this->y=y; } operator double (); private: int x, y; }; Rational:: operator double() { return double(x)/y; } ex11_overload06.cpp
21 .21 自动类型转换注意点 若重载了类型转换函数，则建议用非成员函数方式 实现运算符重载，并且形参使用“ 常引用 ”！ 一个类可以重载类型转换函数实现 对象到基本数据 类型 的转换，也可以转换构造函数实现 基本数据类 型到对象 的转换，但两者 不能并存 ！ Rational operator+ { const Rational &r1, const Rational &r2 }
22 .22 重载运算符建议 运算符 [] 、 ++ 、 -- 、 () 必须以成员函数方式重载 运算符 << 、 >> 必须以非成员函数重载 ( 这两个运算符的重载涉及到输入输出，将在文件流中介绍 ) 算术运算符和关系运算符建议以 非成员函数 重载，以便实现一些简单的自动类型转换
23 .23 1) 使用 成员函数 方式重载复数类的加法和减法，使之能执行下面的运算 2) 使 用非成员函数 方式重载复数的加法和减法运算 ，使之能执行下面的运算 Complex a(2.1,5.7), b(7.5,8), c, d; c = a + b; d = b + 5.6; （程序取名 hw11_01.cpp ） Complex a(2.1,5.7), b(7.5,8), c, d; c = a + b; d = b + 5.6; e = 4.1 + a; （程序取名 hw11_02.cpp ） 思考：能否实现 c = 4.1 + a ？ 上机作业 课后练习（自己练习）
24 .24 3) 使用 成员函数 方式重载有理数的比较运算，即 >, ==, < Rational a(4,5), b(2,3); cout << "a>b? " << (a>b ? "true" : "false") << endl ; cout << "a==b? " << (a==b ? "true" : "false") << endl ; cout << "a<b? " << (a<b ? "true" : "false") << endl ; （程序取名 hw11_03.cpp ） 上机作业
热门城市
