- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
08_Sort
展开查看详情
1 .第八讲 排序算法 —— C++ 实现
2 .2 排序算法 排序 (Sorting) :将 一串数据 依 照指定方式进行排列。 常用排序 方 式:数 值顺 序,字 典顺序 。 时 间复杂度 (最差、平 均): 设有 n 个数据,一般 来说 , 好 的排序算法性 能 是 O ( n log n ) ,差的 性能 是 O ( n 2 ) ,而理 想的性能 是 O ( n ) 。 空间复杂度 : 算法在运行过程中临时占用 存储空间的大小。 稳定排序算 法 :相等的数据维持原有相 对次序
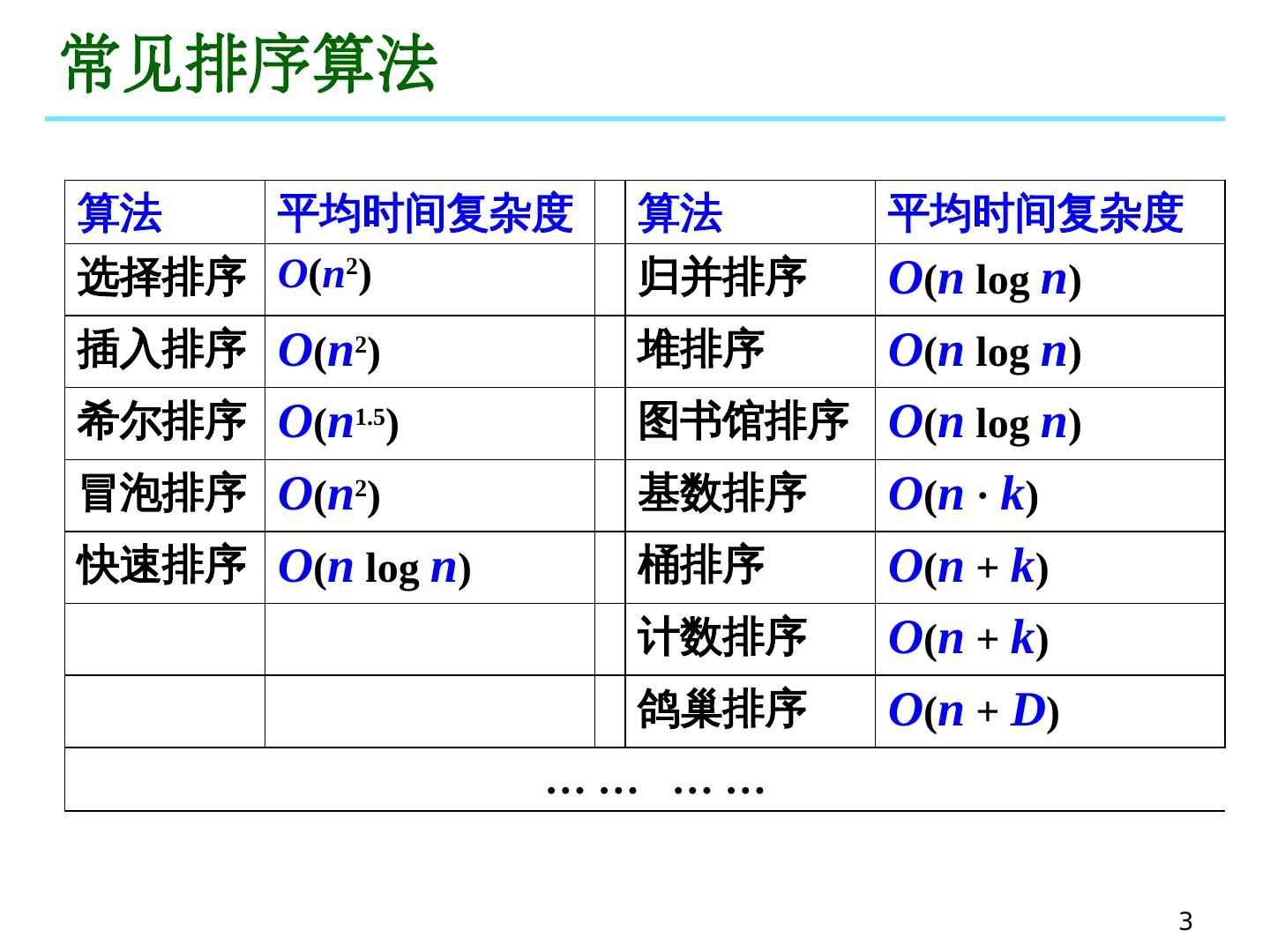
3 .3 常见排序算法 算法 平均时间复杂度 算法 平均时间复杂度 选择排序 O ( n 2 ) 归并排序 O ( n log n ) 插入排序 O ( n 2 ) 堆排序 O ( n log n ) 希尔排序 O ( n 1.5 ) 图书馆排序 O ( n log n ) 冒泡排序 O ( n 2 ) 基数排序 O ( n · k ) 快速排序 O ( n log n ) 桶排序 O ( n + k ) 计数排序 O ( n + k ) 鸽巢排序 O ( n + D ) … … … …
4 .4 主要内容 选择排序 插入排序 希 尔排序 冒泡排序 快速排序 本讲中假定是对数据进行 从小到大 排序
5 .5 一 、选择排 序 找出最小值,将其与第一个位置的 元素进行交换, 然后 对剩余的序列重复以上过程,直至排序结束。 —— 有时也称为 最小排序
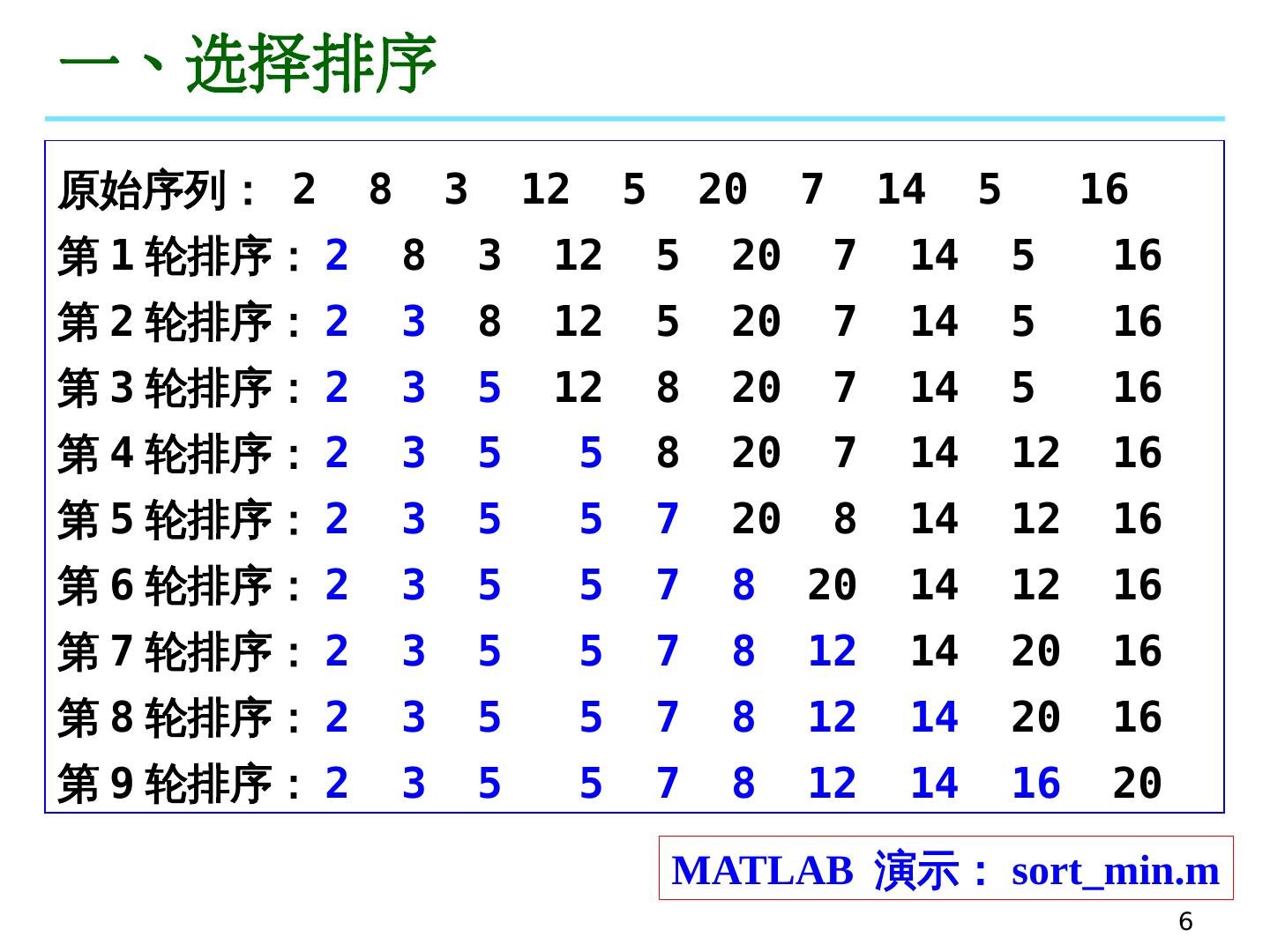
6 .6 一 、选择排 序 原 始 序 列 : 2 8 3 12 5 20 7 14 5 16 第1 轮 排序 : 2 8 3 12 5 20 7 14 5 16 第2 轮 排序 : 2 3 8 12 5 20 7 14 5 16 第3 轮 排序 : 2 3 5 12 8 20 7 14 5 16 第4 轮 排序 : 2 3 5 5 8 20 7 14 12 16 第5 轮 排序 : 2 3 5 5 7 20 8 14 12 16 第6 轮 排序 : 2 3 5 5 7 8 20 14 12 16 第7 轮 排序 : 2 3 5 5 7 8 12 14 20 16 第8 轮 排序 : 2 3 5 5 7 8 12 14 20 16 第9 轮 排序 : 2 3 5 5 7 8 12 14 16 20 MATLAB 演示 : sort_min.m
7 .7 选择 排序 C ++ 程序 // 找出最小值所在的位置 int findm in ( int * px , int n) { int idx =0, xmin =* px ; for ( int i =1; i <n; i ++) if (*( px+i )< xmin ) { xmin =*( px+i ); idx = i ; } return idx ; } // 选择排序 ( 最小排序 ) void sort_ m in ( int * px , int n) { int idx , t; for( int k=0; k<n; k++) { idx = findm in ( px+k,n-k ); t= px [k]; px [k]= px [ k+idx ]; px [ k+idx ]=t; % 交换 } }
8 .8 选择 排序 C ++ 程序 int main () { int x[]={2, 8, 3, 12, 5, 20, 7, 14, 5, 16}; int n, i ; // 获取数据个数 n = sizeof (x)/ sizeof (x[0 ]); cout << "x=
9 .9 二、插入排序 基本思想描述如下: 假设 前面 k 个元素已经按顺序排好了,在排第 k +1 个元素时 ,将其插入到前面已排好的 k 个元素中 ,使得插入后得到的 k +1 个元素组成 的序列仍按值有序 。 然后采用同样的方法排第 k +2 个元素。 以此类推,直到排完 序列的所有元素为止。
10 .10 二、插入排序 原 始序列 : 2 8 3 12 5 20 7 14 5 16 第 1 轮排序 : 2 8 3 12 5 20 7 14 5 16 第 2 轮排序 : 2 3 8 12 5 20 7 14 5 16 第 3 轮排序 : 2 3 8 12 5 20 7 14 5 16 第 4 轮排序 : 2 3 5 8 12 20 7 14 5 16 第 5 轮排序 : 2 3 5 8 12 20 7 14 5 16 第 6 轮排序 : 2 3 5 7 8 12 20 14 5 16 第 7 轮排序 : 2 3 5 7 8 12 14 20 5 16 第 8 轮排序 : 2 3 5 5 7 8 12 14 20 16 第 9 轮排序 : 2 3 5 5 7 8 12 14 16 20 MATLAB 演示 : sort_insert.m
11 .11 插入排序 C++ 程序 关键点: 如何将第 k +1 个元素插入到前面的有序 序列中 假定 序列 为 x 1 , x 2 , …, x k , x k +1 , … 策略: 将 x k +1 依次与 x k , x k- 1 , … 进行比较,直至遇见第一个不大于 x k +1 的元素为止。 优化: 可以将比较与移位同时进行。
12 .12 插入排序 C++ 程序 以第 4 轮为例 2 3 8 12 5 20 7 14 5 16 操作 对象 x[k] 比较方向 2 3 8 12 5 20 7 14 5 16 ① 先比较 ② 后移位 ① ② 2 3 8 12 20 7 14 5 16 5
13 .13 插入排序 C++ 程序 // 插入排序(部分代码) ... ... for(k=1 ; k<n; k++) { key = x[k]; for (i=k-1 ; x[i]> key && i >=0 ; i--) { x[i+1] = x[i]; } x[i+1] = key; } ... ... void sort_insert ( int * px , int n) 留作练习
14 .14 三、希尔排序 又称为“缩小增量排序”( Diminishing Increment Sort ),由 D. Shell 于 1959 年提出,是 对插入排序 的改进 。
15 .15 三、希 尔排 序 基本过程描述如下: 把 序列按照某个 增量( gap ) 分成 几个子序列,对这几个子序列进行 插入排序。 不断 缩小增量 ,扩大 每个子序列的元素 数量,并对每个子序列进行插入排序。 当增量 为 1 时,子 序列 就是整个序列, 而此时 序列已经 基本有序 了, 因此 只需做 少量的比较和移动就可以完成 对整个序列 的排序。 出发点 :插入排序 在元素基本有序的情况 下,效率很高 gap :初始值设为 n/2 ,然后不断减半。
16 .16 三、希 尔排 序 2 8 3 12 5 20 7 14 5 16 第一轮: gap=10/2=5 2 8 3 12 5 20 7 14 5 16 第一轮排序后 2 7 3 5 5 20 8 14 12 16
17 .17 三、希 尔排 序 2 7 3 5 5 20 8 14 12 16 第二轮: gap=gap/2=2 2 7 3 5 5 20 8 14 12 16 第二轮排序后 2 5 3 7 5 14 8 16 12 20
18 .18 三、希 尔排 序 第三轮: gap=gap/2=1 第三轮排序后 2 5 3 7 5 14 8 16 12 20 2 3 5 5 7 8 12 14 16 20 在最坏的情况下, 插入排序 需要 O ( n 2 ) 次移位操作,而 希尔排序 只需 O ( n 1.5 ) 次移位操作。 例 :以 n =8 为例,统计最坏情况下插入排序与希尔排序的移位操作次数 MATLAB 演示 : sort_shell.m
19 .19 希尔排序 C++ 程序 void sort_ shell ( int * px , int n) 留作练习
20 .20 四、冒泡排序 基本过程描述如下: 走访需要排序的序列,比较 相邻的两个元素,如果他们的顺序错误就把他们交换过来 。 不断重复上述过程 ,直到没有元素需要交换, 排序结束。 这个算法的名字由来是因为越大的元素会经由交换慢慢“ 浮 ”到数列的顶端。
21 .21 四、冒泡排序 8 14 16 5 20 x 5 x 4 x 3 x 2 x 1 8 14 16 20 5 8 14 20 16 5 8 20 14 16 5 20 8 14 16 5 MATLAB 演示 : sort_bubble.m
22 .22 四、冒泡排序 具体 过程 可以描述为 : 将第 1 个和第 2 个元素进行比较 ,如果前者大于后者,则交换两者的位置, 否则位置不变;然后将第 2 个元素与第 3 个元素进行比较 ,如果前者大于后者,则交换两者的位置,否则位置不变 ;依此类推 ,直到最后两个元素比较完毕为止 。这就是第一 轮 冒泡 过程 , 这个过程 结束 后 , 最大的元素就 “浮”到 了最后一个位置上 。 对前面 n -1 个元素进行第二 轮 冒泡排序 , 结束后, 这 n -1 个元素中的最大值 就被 安放在了 第 n -1 个 位置上 。 对前面的 n -2 个元素进行第三轮冒泡排序 。 以此类推 , 当 执行完第 n -1 轮冒泡 过程 后,排序 结束 。
23 .23 冒泡排序 C++ 程序 冒泡排序的 进一步优化 :如果 有 100 个数的数组,仅前面 10 个无序,后面 90 个都已排好序且都大于前面 10 个数字,那么在 第一轮冒泡过程后 ,最后发生交换的位置必定小于 10 ,且这个位置之后的数据必定已经有序了,记录下这位置,第二次只要从数组头部遍历到这个位置就可以了。 冒泡排序的 优化 :如果在某轮冒泡过程中没有发生元素交换,这说明整个序列已经排好序了,这时就不用再进行后面的冒泡过程,可以直接结束程序。 void sort_ bubble ( int * px , int n) 留作练习
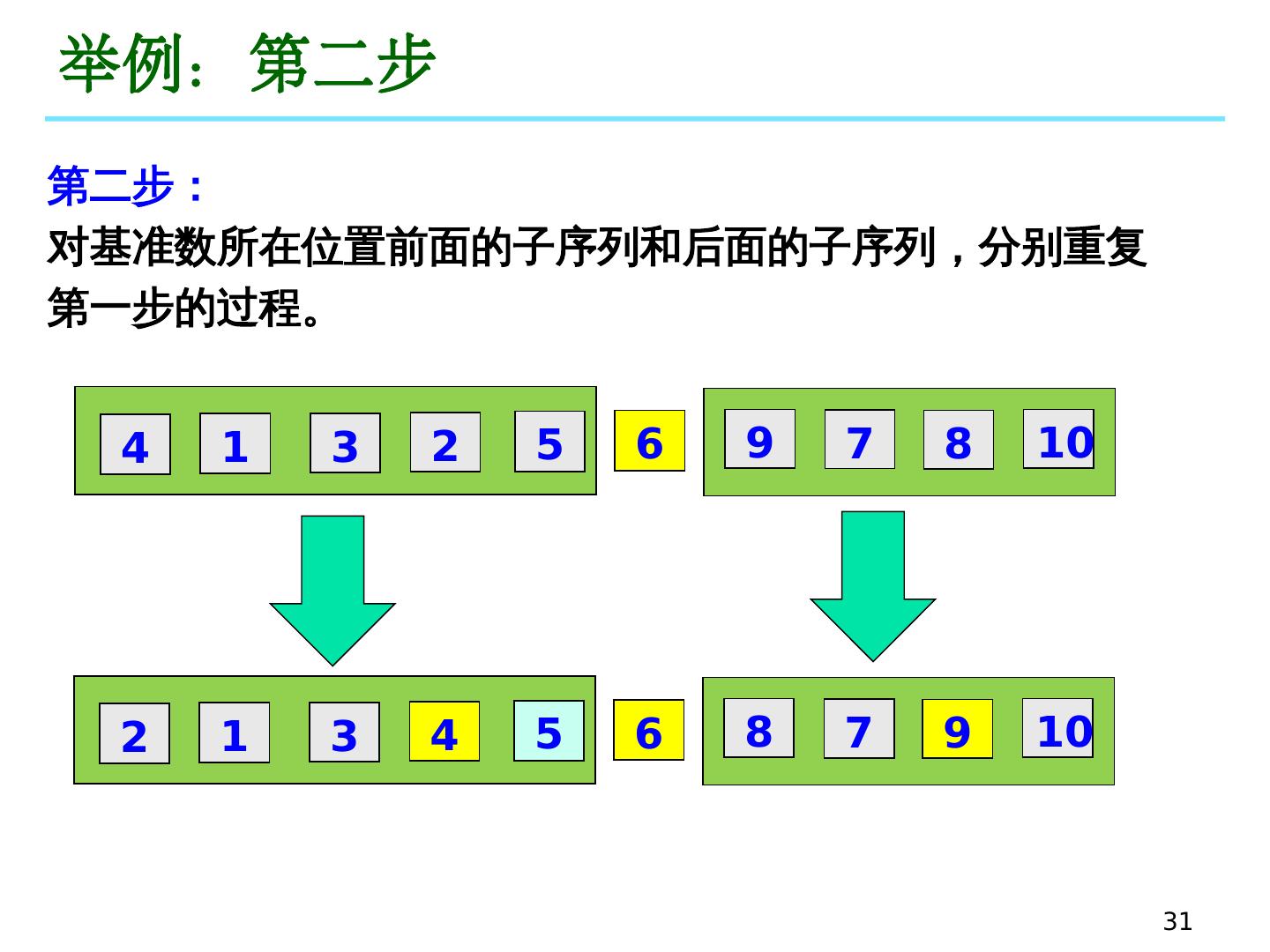
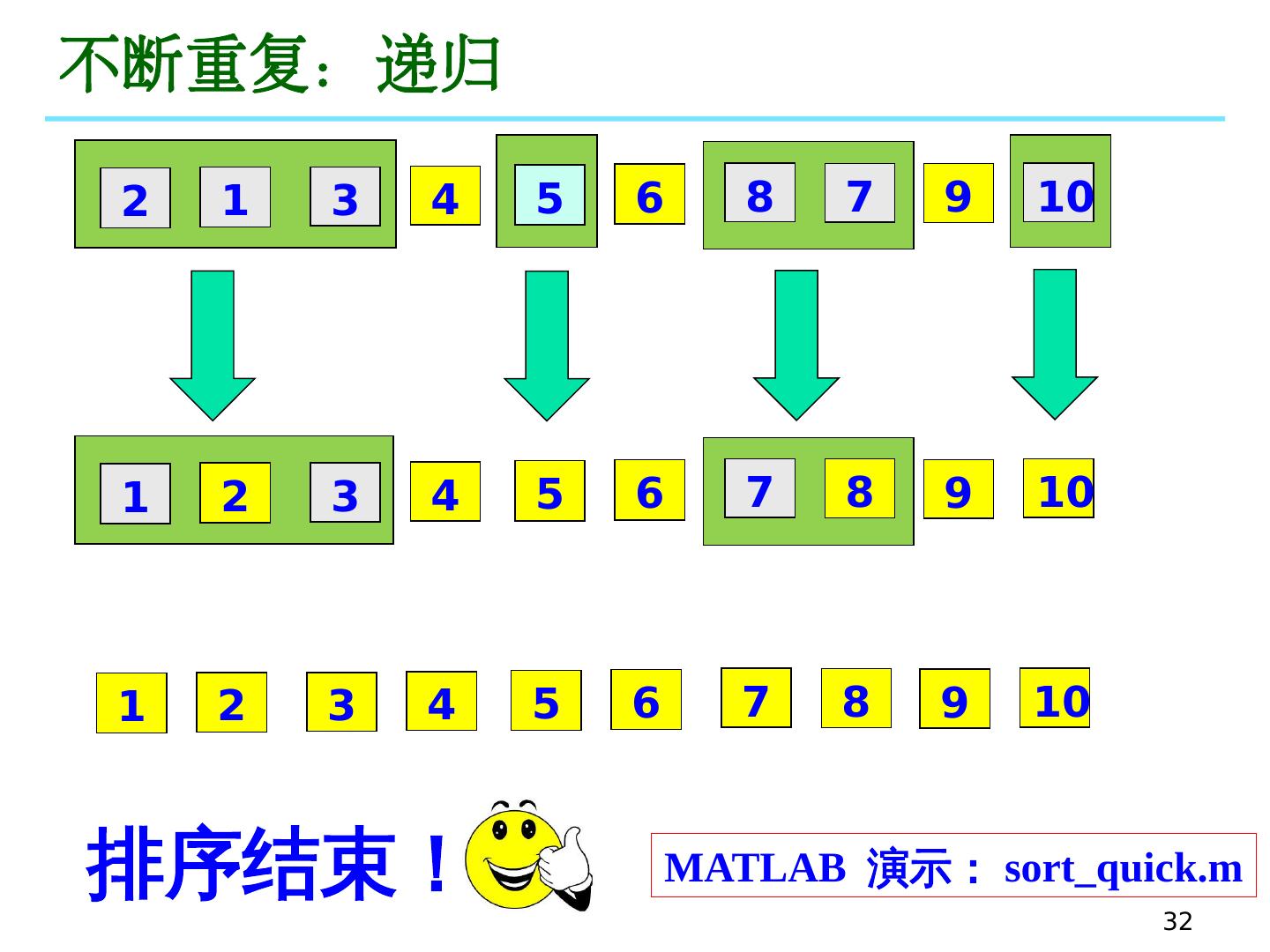
24 .24 五、快速排序 快速排序采用的是 分而治之 思想: 将原问题分解为若干个规模更小但结构与原问题相似的子 问题,然后递归求解 这些子问题 ,最后将 这些子问题的解组合为原问题的解。 —— 是 目前最常用的排序算法 之一
25 .25 五、快速排序 具体 过程 可以描述为 : 随机选 定其中一 个元素作为 基准数( pivot ) (通常采用第一个元素),然后通过循环和比较运算,将 原序列分割成两部分,使 得新序列中在 该基准数 前面的 元素都小 于等于这个元 素, 而其后面的 元素都大于等于这 个元 素 。 (这时基准数已经归位) 依此类推 ,再对这两个分割好的子序列进行上 述过 程,直到排序结束 。 (递归思想,分而治之)
26 .26 快 速排 序 第一 步的具体实现方法: (假定基准数的原始位置是 i 1 =1 ) 先从原序列的 最右边 开始, 往左 找出第一个小于 6 的数,然后将该数与基准数交换位置,设基准数新位置为 i 2 从 i 1 右 边的位置开始, 往右 找出第一个大于 6 的数,然后将该数与基准数交换位置, 设基准数新位置为 i 3 从 i 2 左边 的位置开始 , 往左 找出第一个小于 6 的数,然后将该数与基准数交换位置,设基准数新位置为 i 4 从 i 3 右边的位置开始, 往右 找出第一 个大于 6 的数,然后将该数与基准数交换位置 , 设基准数新位置为 i 5 不断重复以上过程, 遍历整个序列 原 始 序 列: 6 1 3 7 5 9 2 4 8 10
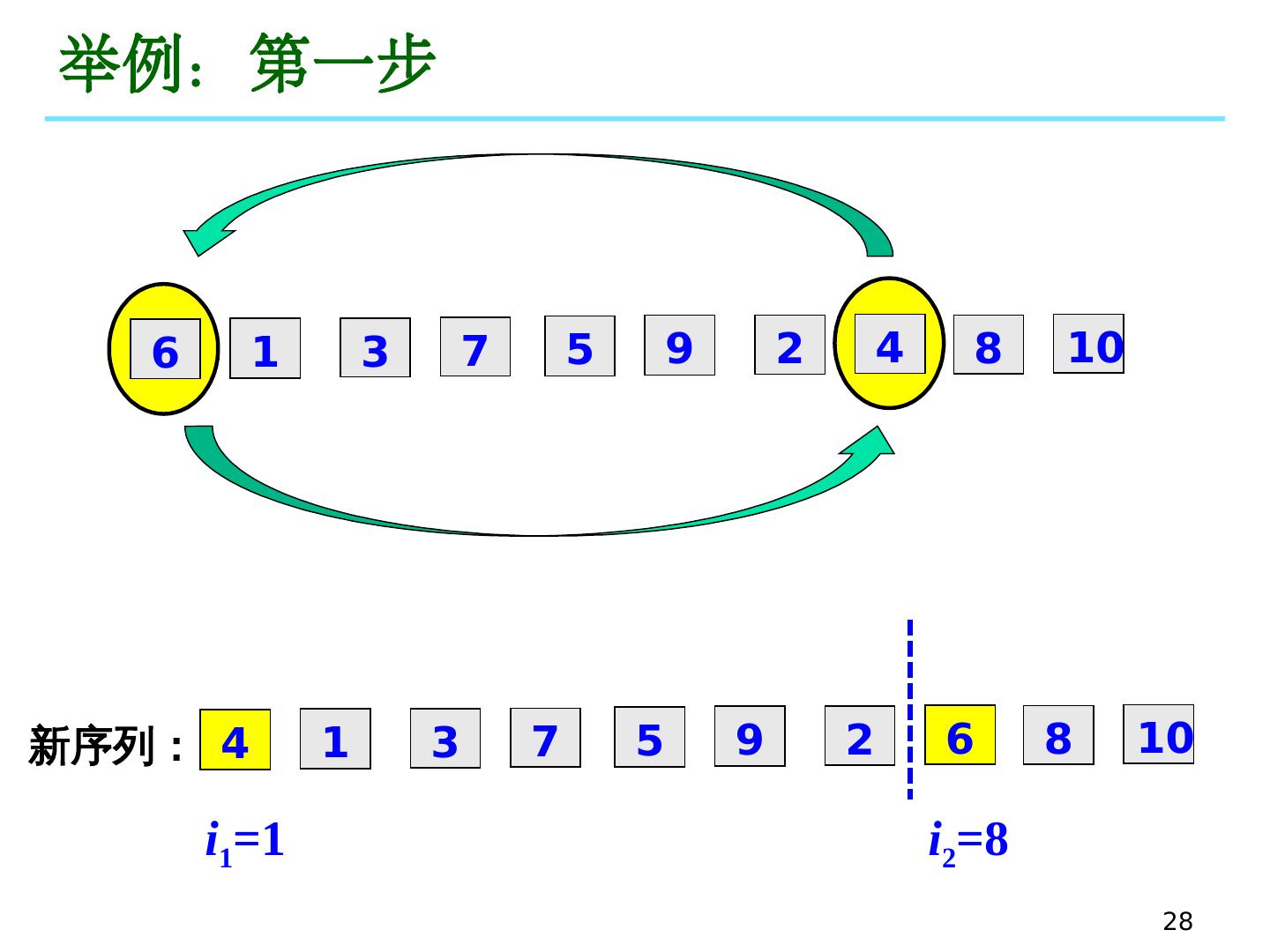
27 .27 快 速排 序举例 原 始 序 列: 第一步: 我们选第一个元素为基准数,即将 6 作为基准数。我们的目标是得到一个新序列,使得在这个新序列中, 排 在 6 前面的数字都小于 6 ,而排在 6 后面的数字都不小于 6 。 6 1 3 7 5 9 2 4 8 10 搜索起始位置 6 1 3 7 5 9 2 4 8 10 基准数 需交换位置的数 搜索 i 1 =1
28 .28 举例:第一步 6 1 3 7 5 9 2 4 8 10 4 1 3 7 5 9 2 6 8 10 新序 列: i 1 =1 i 2 =8
29 .举例:第一步 新序 列: 4 1 3 7 5 9 2 6 8 10 4 1 3 7 5 9 2 6 8 10 基准数 搜索 需交换位置的数 新序 列: 4 1 3 6 5 9 2 7 8 10 i 1 =1 i 2 =8 i 3 =4 25