- 快召唤伙伴们来围观吧
- 微博 QQ QQ空间 贴吧
- 文档嵌入链接
- 复制
- 微信扫一扫分享
- 已成功复制到剪贴板
01_Intro
展开查看详情
1 .第一讲 计算机基础 —— 信息的表示与存储 —— 算法
2 .2 主要内容 信息的表示与存储 算法基本概念 计算机的数字系统 常见的进制数及它们之间的转换 原码,反码与补码 非数值信息的表示
3 .3 计算机数字系统 计算机内部的信息的分类 信息 控制信息:指令和控制字 数据信息 数值信息:定点数与浮点数 非数值信息:字符数据与逻辑数据
4 .4 信息的存储单位 基本单位:位与字节 计算机的最小存储单元是字节( Byte ) 一个字节由 8 个二进制位( bit )组成 其它单位 1 KB = 1024 B 1 MB = 1024 K 1 GB = 1024 M 1 TB = 1024 G 1 PB = 1024 T 1 EB = 1024 P … … 一个英文字符占一个字节,一个汉字占两个字节 计算机 的最小存储单元是字节( Byte ),一个字节由 8 个二进制位( bit )组成。
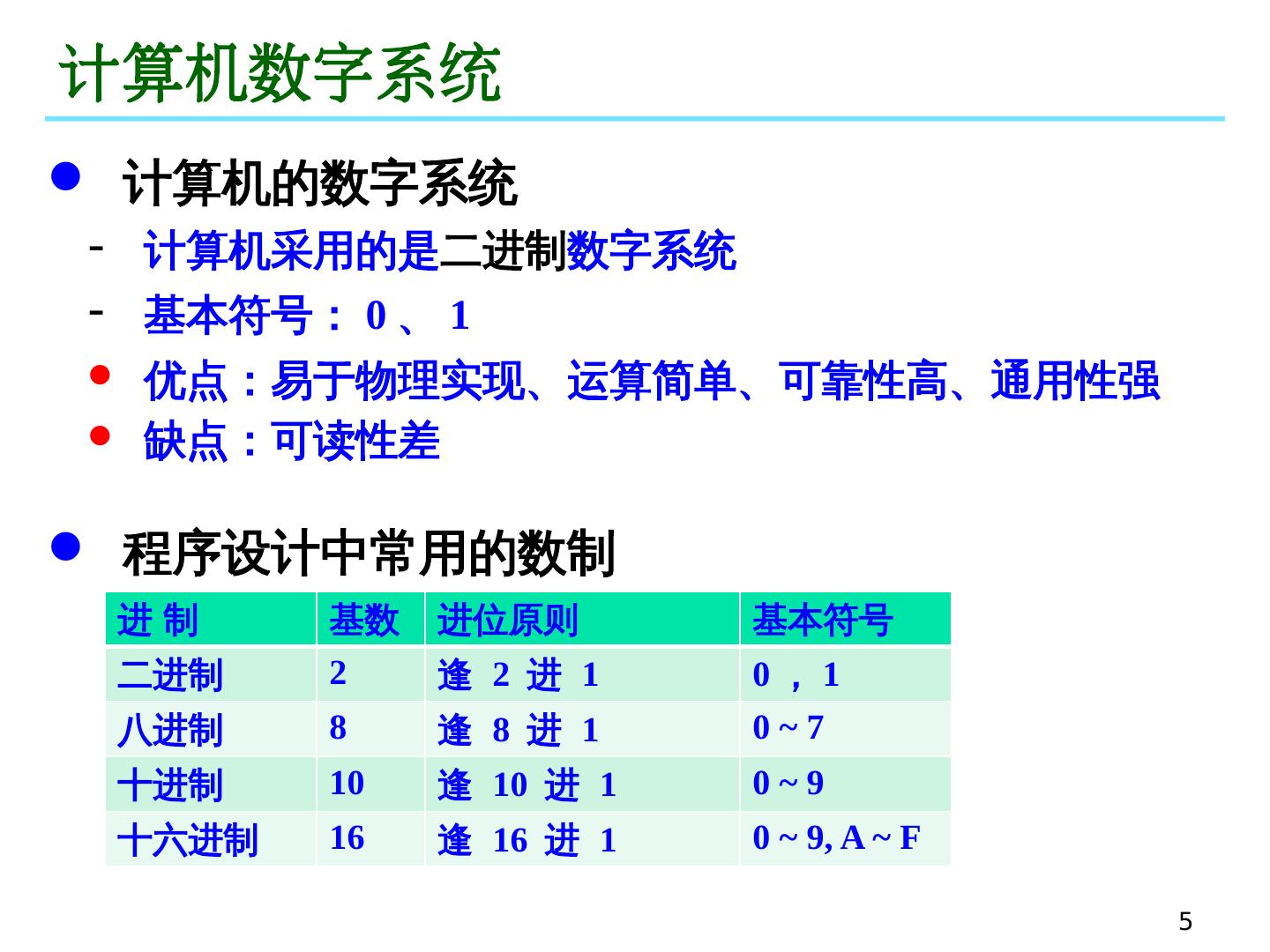
5 .5 计算机数字系统 计算机的数字系统 计算机采用的是 二进制 数字系统 基本符号: 0 、 1 优点:易于物理实现、运算简单、可靠性高、通用性强 缺点:可读性差 程序设计中常用的数制 进 制 基数 进位原则 基本符号 二进制 2 逢 2 进 1 0 , 1 八进制 8 逢 8 进 1 0 ~ 7 十进制 10 逢 10 进 1 0 ~ 9 十六进制 16 逢 16 进 1 0 ~ 9, A ~ F
6 .6 不同进制之间的转换 二进制、八进制、十六进制 转化为 十进制 各位数字与它的权相乘,然后相加 例如 : (101.11) 2 = 1×2 2 + 0×2 1 + 1×2 0 + 1×2 -1 + 1×2 -2 = (5.75) 10 (506.2) 8 = 5×8 2 + 0×8 1 + 6×8 0 + 2×8 -1 = (326.25) 10 (10.C) 16 = 1 × 16 1 + 0× 16 0 + 12×16 -1 = (16.75) 10
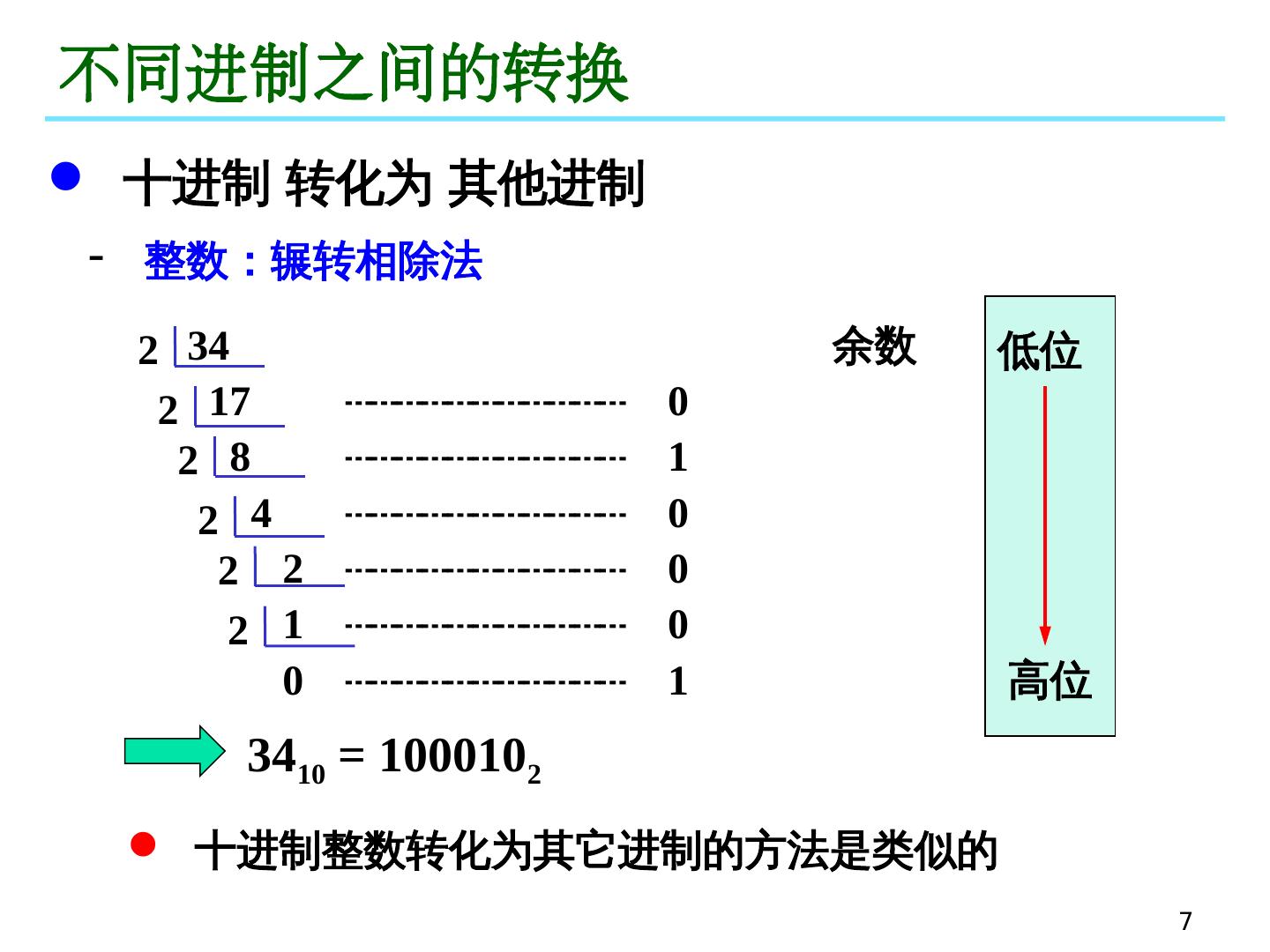
7 .7 不同进制之间的转换 十进制 转化为 其他进制 整数:辗转相除法 34 余数 17 ┄┄┄┄┄┄┄┄┄┄┄ 0 8 ┄┄┄┄┄┄┄┄┄┄┄ 1 4 ┄┄┄┄┄┄┄┄┄┄┄ 0 2 ┄┄┄┄┄┄┄┄┄┄┄ 0 1 ┄┄┄┄┄┄┄┄┄┄┄ 0 0 ┄┄┄┄┄┄┄┄┄┄┄ 1 2 2 2 2 2 2 低位 高位 34 10 = 100010 2 十进制整数转化为其它进制的方法是类似的
8 .8 不同进制之间的转换 十进制的数转化为其他进制 纯 小数:与 2 相乘后取整数部分 例如 : 0.3125×2 = 0 . 625 0.625 ×2 = 1 . 25 0.25 ×2 = 0 . 5 0.5 ×2 = 1 . 0 0.3125 10 = 0.0101 2 每次相乘后去掉整数部分,不断乘下去,直到 小数部分为 0 或 达到指定的精度 为止,然后取每次相乘后的整数部分即可。 绝大部分浮点数无法用二进制精确表示,如 0.1
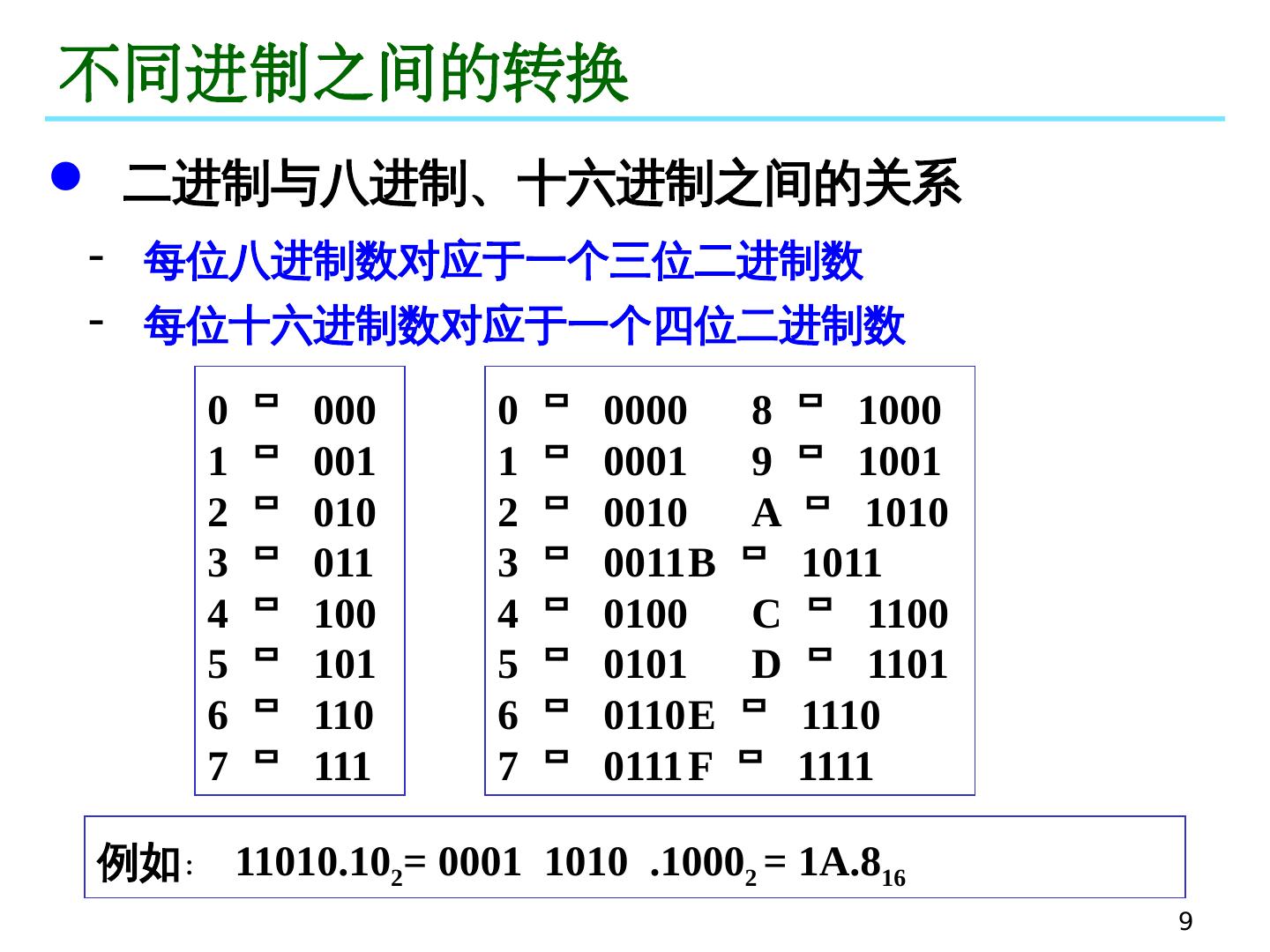
9 .9 不同进制之间的转换 二进制与八进制、十六进制之间的关系 每位八进制数对应于一个三位二进制数 每位十六进制数对应于一个四位二进制数 0 000 1 001 2 010 3 011 4 100 5 101 6 110 7 111 0 0000 8 1000 1 0001 9 1001 2 0010 A 1010 3 0011 B 1011 4 0100 C 1100 5 0101 D 1101 6 0110 E 1110 7 0111 F 1111 例如 : 11010.10 2 = 0001 1010 .1000 2 = 1A.8 16
10 .10 二进制数的编码表示 数在计算机内部的存储方式:原码、反码、补码 数的表示:符号 + 大小 - 符号:用“ 0 ”表示正,用“ 1 ”表示负,放在最高位 - 大小:二进制 34 0 0100010 -34 1 0100010 符号位 优点:直观 缺点:零的表示不唯一;四则运算要考虑符号位,规则复杂 注:这里假定用一个字节存放数据
11 .11 反码 反码一般不直接使用,通常是作为求补码的中间码 正数的反码:与原码相同; 负数的反码: 符号位不变 ,其它位取反( 0 变 1 , 1 变 0 ) 34 0 0100010 0 0100010 -34 1 0100010 1 1011101 原码 反码
12 .12 补码 0 的补码表示唯一,且可以多表示一个数 对补码再求补即得到原码 正数的补码:与原码相同; 负数的补码:反码的最末位加 1 计算机是以补码方式存放数据的! 34 0 0100010 0 0100010 0 0100010 -34 1 0100010 1 1011101 1 1011110 原码 反码 补码
13 .13 补码运算规则 符号位可以作为数值参加运算 减法可以转化为加法运算 运算结果仍为补码 例: 用 8 位字长计算 67 - 10 67 10 = 01000011 2 [ 原 码 ] 01000011 [ 补码 ] -10 10 = 10001010 2 [ 原 码 ] 11110101 [ 反码 ] 11110110 [ 补码 ] 01000011 + 11110110 = 1 00111001 00111001 ( 注意: 符号位 加入正常运算,超出字长部分 自然丢失 ) 00111001 [ 补码 ] 00111001 2 [ 原 码 ] = 57 例: 用 8 位字长计算 85 + 44 ,会出现什么问题?
14 .14 非数值信息 西文字符: ASCII 码 中文汉字:一个汉字占两个字节,常见编码有 GB2312 、 GBK 、 GB18030 、 UTF-8 完整的 ASCII 码表见课程主页或教材 非数值信息的表示
15 .15 算法基本概念 什么是算法 算法的特征与评价 算法的描述方法与基本控制结构
16 .16 算法 程序 = 算法 + 数据结构 + 程序设计方法 + 语言工具和环境 算法: 为解决一个问题而采取的方法和具体步骤 —— 著名计算机科学家 Nikiklaus Wirth , 1976 对数据组织的描述:数据的类型和组织形式,即 数据结构 对操作流程的描述:即操作步骤,也就是 算法 一个程序应该包括: 学习程序设计的目的不仅仅是学习一种特定的语言, 而是学习进行程序设计的 一般方法 。 掌握了算法就是掌握了 程序设计的灵魂 ,再配合有关的计算机语言, 就能顺利编写出程序,解决问题。 脱离了具体的语言去学习程序设计是困难的。
17 .17 算法 空间复杂度 时间复杂度 实现复杂度 算法性能的评测 输入: 有零个或多个输入量 输出: 通常有一个或以上输出量(计算结果) 明确性: 算法的描述必须无歧义,保证算法的正确执行 有限性: 有限个输入、有限个指令、有限个步骤、有限时间 有效性: 又称可行性,能够通过有限次基本运算来实现 算法的特征
18 .18 算法描述与基本结构 算法的描述方法: 自然语言、 流程图 、 NS 流程图、伪代码 流程图:简洁、直观、准确 算法的三种基本控制结构 顺序结构 选择结构 循环结构
19 .19 顺序结构 A B A A B A B A 顺序结构是最基本、也是最常用的程序设计结构,它按照程序语句行的自然顺序,一条一条地执行程序。
20 .20 选择结构 A B p Y N 当 p 为“真” 当 p 为“假” 选择结构,又称分支结构或条件结构,包括简单选择和多分支选择结构,可根据条件,判断应该选择哪一条分支来执行。
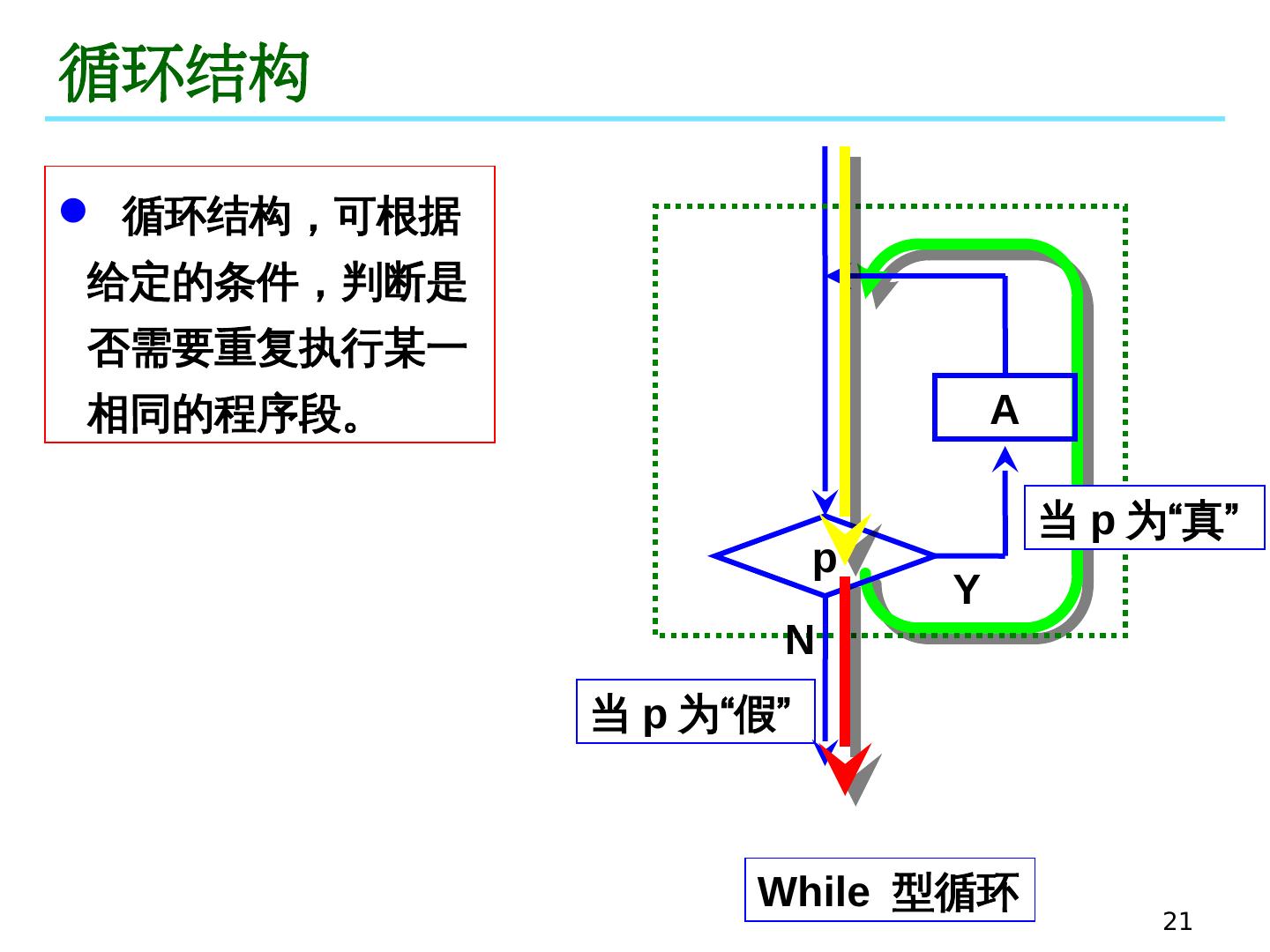
21 .21 循环结构 A p Y While 型循环 N 当 p 为“真” 当 p 为“假” 循环结构,可根据给定的条件,判断是否需要重复执行某一相同的程序段。
22 .22 循环结构 三种结构的共同点: 只有一个入口 只有一个出口 结构内每一部分都有机会被执行 结构内不存在“死循环”
23 .23 小结 算法的基本概念 算法的三种控制结构 了解以下内容 不同进制之间的转换 掌握以下内容
24 .24 课后练习 1 、将下列二进制数转化为十进制数 101, 100111, 11010.011 2 、将下列十进制数转化为二进制数 101, 0.5625, 93.328125 思考: 小数的补码如何计算?